微型力量,巨大作用:嵌入式技术的创新应用
微型力量,巨大作用:嵌入式技术的创新应用
嵌入式技术是一种将计算机技术嵌入到各种设备和系统中的技术,它的应用范围非常广泛,包括但不限于智能手机、智能家居、医疗设备、工业自动化等领域。这种微型的技术在各个领域中发挥着巨大的作用,推动着技术的创新和进步。
智能手机
智能手机是嵌入式技术的一个典型应用。通过嵌入式系统,智能手机可以实现各种功能,如通信、定位、计算、拍照、录像等。嵌入式技术使得智能手机可以变得更加智能、便捷、高效,极大地改善了人们的生活方式。
智能家居
智能家居是近年来嵌入式技术的一个热门应用领域。通过将嵌入式系统应用于家居设备中,人们可以实现远程控制、智能化管理、节能环保等功能。智能家居的出现,让人们的生活更加便捷、舒适,也提升了家居设备的智能化水平。
医疗设备
在医疗领域,嵌入式技术也发挥着重要作用。通过嵌入式系统,各种医疗设备可以实现监测、诊断、治疗等功能,提高了医疗水平和效率。例如,心脏起搏器、血糖监测仪等设备都是嵌入式技术的应用,帮助患者更好地管理健康状况。
工业自动化
在工业领域,嵌入式技术被广泛应用于各种自动化设备和系统中,如机器人、传感器、控制系统等。这些嵌入式系统可以实现生产线的智能化管理、自动化控制,提高了生产效率和产品质量,推动了工业生产的发展。
我整理了一些资料https://m.hqyjai.net/emb_study_blue_short.html?xt=yj
总之,嵌入式技术作为一种微型力量,在各个领域中发挥着巨大的作用,推动着技术的创新和进步。随着科技的不断发展,嵌入式技术的应用范围将会更加广泛,为人类的生活和工作带来更多便利和可能性。
相关文章:

微型力量,巨大作用:嵌入式技术的创新应用
微型力量,巨大作用:嵌入式技术的创新应用 嵌入式技术是一种将计算机技术嵌入到各种设备和系统中的技术,它的应用范围非常广泛,包括但不限于智能手机、智能家居、医疗设备、工业自动化等领域。这种微型的技术在各个领域中发挥着巨…...
华为 OD 一面算法原题
2.2 亿彩票公布调查结果 昨天,闹得沸沸扬扬的《10 万中 2.2 亿》的彩票事件,迎来了官方公告。 简单来说,调查结果就是:一切正常,合规合法。 关于福利彩票事件,之前的推文我们已经分析过。 甚至在后面出现《…...
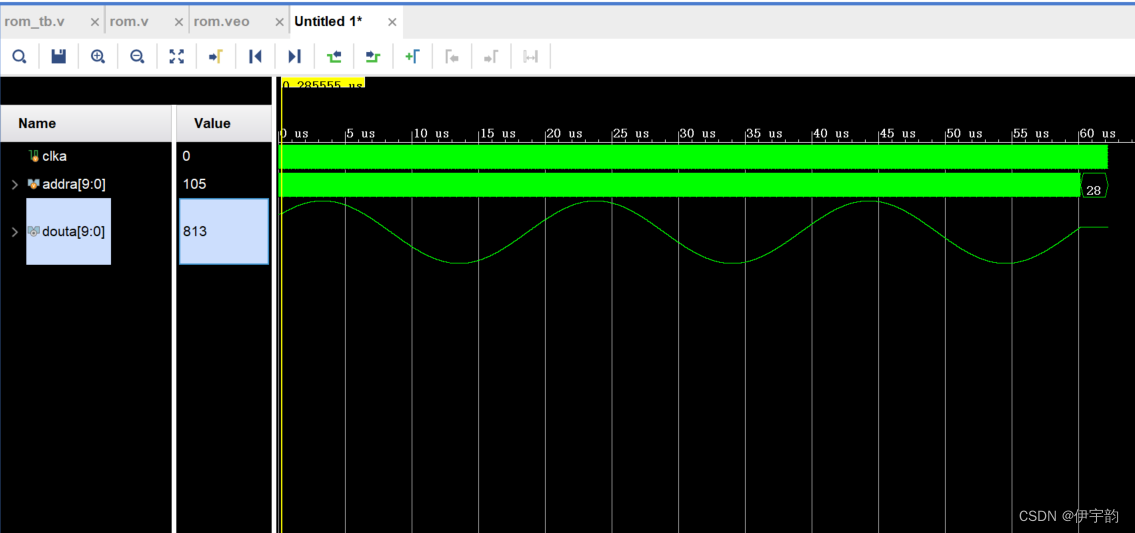
FPGA-学会使用vivado中的存储器资源ROM(IP核)
问题: 某芯片,有500个寄存器,需要在上电的时候由FPGA向这些寄存器中写入初始值,初始值已经通过相应的文档给出了具体值,这些值都是已知的。 分析关键点: 数据量比较多(Verilog代码,通过case语句、always语句这种查找表的方式,数…...

自测-1 打印沙漏
文章预览: 题目算法代码 题目 算法 以前做过这个,那次是c语言写的,一点一点处理一层一层完成,这次我换了一种语言用了另一种思想使用递归去写,还是我们要先求出应该有多少层这个很容易,中间输出部分我们算…...
)
高级语言期末2009级B卷(计算机学院)
1.编写一个名为mystrcpy的函数,实现将字符串str1的偶数位子的字符的拷贝到另一个字符串str2中。并编写主函数,在主函数中从键盘读入一个长度<100的字符串str1,然后调用函数mystrcpy;最后输出str2,例如,读…...

c# using 用法
using命令空间 导入命名空间中的所有类型 如:using System.Text; using别名 using别名包括详细命名空间信息的具体类型,这种做法有个好处就是当同一个cs引用了两个不同的命名空间,但两个命名空间都包括了一个相同名字的类型的时候。当需要…...

【Django】执行查询—跨关系查询中的跨多值关联问题
跨多值查询 跨越 ManyToManyField 或反查 ForeignKey (例如从 Blog 到 Entry )时,对多个属性进行过滤会产生这样的问题:是否要求每个属性都在同一个相关对象中重合。 filter() 先看filter(),通过一个例子看…...

Spring八股 常见面试题
什么是Spring Bean 简单来说,Bean 代指的就是那些被 IoC 容器所管理的对象。我们需要告诉 IoC 容器帮助我们管理哪些对象,这个是通过配置元数据来定义的。配置元数据可以是 XML 文件、注解或者 Java 配置类。 将一个类声明为 Bean 的注解有哪些? Com…...

今年面试潮,说实话这个开发岗能不能冲?
自打华为 2019 年发布鸿蒙操作系统以来,网上各种声音百家争鸣。尤其是 2023 年发布会公布的鸿蒙 4.0 宣称不再支持 Android,更激烈的讨论随之而来。 当下移动端两大巨头瓜分了绝大部分市场: iOS 是闭源的,只有唯一的一家厂商&am…...
【前端素材】推荐优质在线花卉商城电商网页Flowery平台模板(附源码)
一、需求分析 1、系统定义 在线花卉商城是一个通过互联网提供花卉销售服务的电子商务平台,用户可以在该平台上浏览、选择和购买各种花卉产品。 2、功能需求 在线花卉商城是一个通过互联网提供花卉销售服务的电子商务平台,用户可以在该平台上浏览、选…...
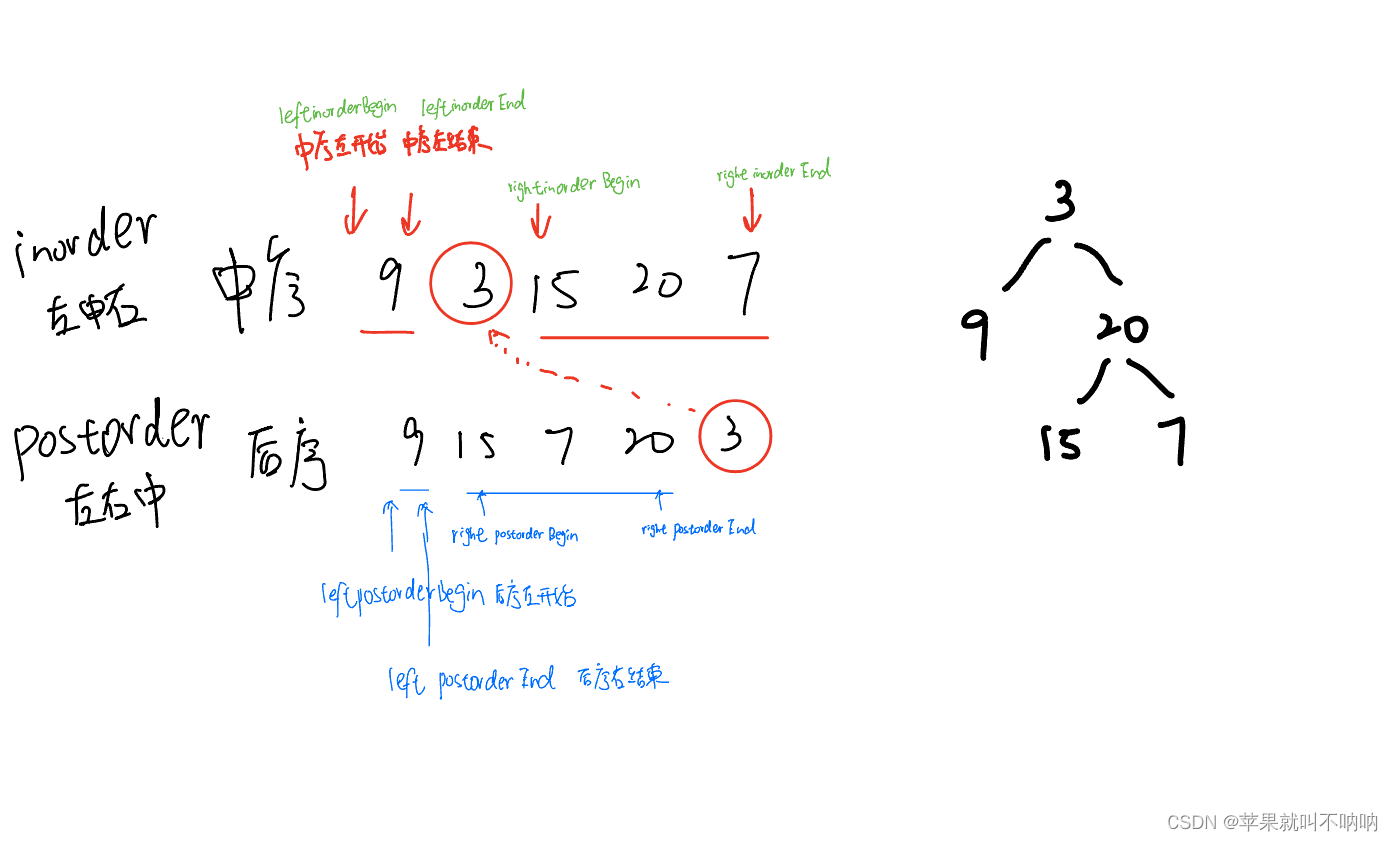
★【递归】【构造二叉树】Leetcode 106.从中序与后序遍历序列构造二叉树
★【递归前序】【构造二叉树】Leetcode 106.从中序与后序遍历序列构造二叉树 105. 从前序与中序遍历序列构造二叉树 106.从中序与后序遍历序列构造二叉树:star:思路分析递归解法 105. 从前序与中序遍历序列构造二叉树递归解法 凡是构造二叉树>>>>>>>>&…...

linux检测和重启python脚本
#!/bin/bash# 检测Flask应用是否挂了 if ! pgrep -f "flask_app.py" >/dev/null; then# 重启Flask应用cd /path/to/your/flask/appnohup python3 flask_app.py >/dev/null 2>&1 & fi这是一个简单的bash脚本,用于检测Flask应用是否挂掉&a…...

HTML+CSS+JS:花瓣登录组件
效果演示 实现了一个具有动态花朵背景和简洁登录框的登录页面效果。 Code <section><img src"./img/background.jpeg" class"background"><div class"login"><h2>Sign In</h2><div class"inputBox"…...

Unity中URP下实现水体(水面反射)
文章目录 前言一、原理1、法一:使用立方体纹理 CubeMap,作为反射纹理使用2、法二:使用反射探针生成环境反射图,所谓反射的采样纹理 二、实现水面反射1、定义和申明CubeMap2、反射向量需要什么3、计算 N ⃗ \vec{N} N 4、计算 V ⃗…...

基于FastJson实现Json数据文件导入导出解析
哈喽,大家好,我是灰小猿,一个超会写bug的程序猿! 今天来记录一个在项目实战中比较实用的方法,主要是针对一些需要存在简单数据文件导入导出的场景,如:数据文件的简单备份、软件升版前后配置导入…...

JVM内存分配与垃圾收集流程
3.8 实战:内存分配与回收策略 3.8.1 对象优先在Eden分配 大多数情况下,对象在新生代Eden区中分配。当Eden区没有足够空间进行分配时,虚拟机将发起一次Minor GC。 3.8.2 大对象直接进入老年代 HotSpot虚拟机提供了-XX:Prete…...

【python】yaml转成json
姊妹篇:【python】json转成成yaml yaml数据: address:city: 北京市postalCode: 100000street: 北京路123号 age: 30 cart: - product:name: 笔记本电脑price: 1199.99quantity: 2 - product:name: 智能手机price: 599.99quantity: 1 children: - age: …...

css5定位
css 一.定位1.概念(定位定位模式边位移)2.静态位移static(不常用)3.相对定位relative(不脱标)(占位置)4.绝对定位absolute(脱标)(不占位置&#x…...

【解决】修改 UI界面渲染层级 的常见误区
开发平台:Unity 2021版本 问题描述 Unity 中管理 UI 上显示元素的前后层级关系大致为以下两种方式: 方式一:修改UI元素队列顺序与层级方式二:使用 Canvas 组件中的 Override Sort 属性配置 方式二 对应复杂的 UI 层级关系将常…...

蓝桥杯练习系统(算法训练)ALGO-995 24点
资源限制 内存限制:256.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s 问题描述 24点游戏是一个非常有意思的游戏,很流行,玩法很简单:给你4张牌,每张牌上有数…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
