python笔记_进制
二进制
进位规则:满2进1
范围:0,1
符号:以0b和0B开头
八进制
进位规则:满8进1
范围:0-7
符号:以0o和0O开头
十进制
进位规则:满10进1
范围:0-9
十六进制
进位规则:满16斤1
范围:0-9加上A(10)-F(15) ——a-f不区分大小写
符号:以0x和0X开头
A,其他进制转十进制
1,二转十
规则:从低位(最右边)开始,将每个位上的数提出来,乘以2的(位数减一)次方,最后求和
例:
0b1011
——>
1*2的(1-1)次方 + 1*2的(2-1)次方 + 0*2的(3-1)次方 +1*2的(4-1)次方
=1+2+0+8
=11
2,八转十
规则:从低位(最右边)开始,将每个位上的数提出来,乘以8的(位数减一)次方,最后求和
例:
0o234
——>
4*8的(1-1)次方 + 3*8的(2-1)次方 + 2*8的(3-1)次方
=4+24+128
=156
3,十六转十
规则:从低位(最右边)开始,将每个位上的数提出来,乘以16的(位数减一)次方,最后求和
例:
0x23A
——>
10*16的(1-1)次方 + 3*16的(2-1)次方 + 2*16的(3-1)次方
=10+48+512
=570
B,十进制转其他进制
1,十转二
规则:不断除以二,直到商为0为止,最后将每步得到的余数倒过来
例:
bin(34)
——>34余0,17余1,8余0,4余0,2余0,1
0b100010
2,十转八
规则:不断除以八,直到商为0为止,最后将每步得到的余数倒过来
例:
oct(131)
——>131余3,16余0,2余0,2
0o203
3,十转十六
规则:不断除以十六,直到商为0为止,最后将每步得到的余数倒过来
例:
hex(237)
——>237余D,E
0xED
C,二转八,二转十六
1,二转八
规则:从低位开始,每三位一组转为十进制,最后转成对应的八进制
例
0b11010101
——>325
0o325
2,二转十六
规则:从低位开始,每四位一组转为十进制,最后转成对应的十六进制
例
0b11010101
——>13 5
0xD5
D,十六转二,八转二
1,十六转二
规则:将十六进制每一位,转为十进制,最后转成对应的,一个四位的二进制数
例
0x23B
——>2 3 11
——>0010 0011 1011
0b1000111011
2,八转二
规则:将八进制每一位,转为十进制,最后转成对应的,一个三位的二进制数
例
0o237
——>2 3 7
——>010 011 111
0b10011111
相关文章:

python笔记_进制
二进制 进位规则:满2进1 范围:0,1 符号:以0b和0B开头 八进制 进位规则:满8进1 范围:0-7 符号:以0o和0O开头 十进制 进位规则:满10进1 范围:0-9 十六进制 进位规则ÿ…...
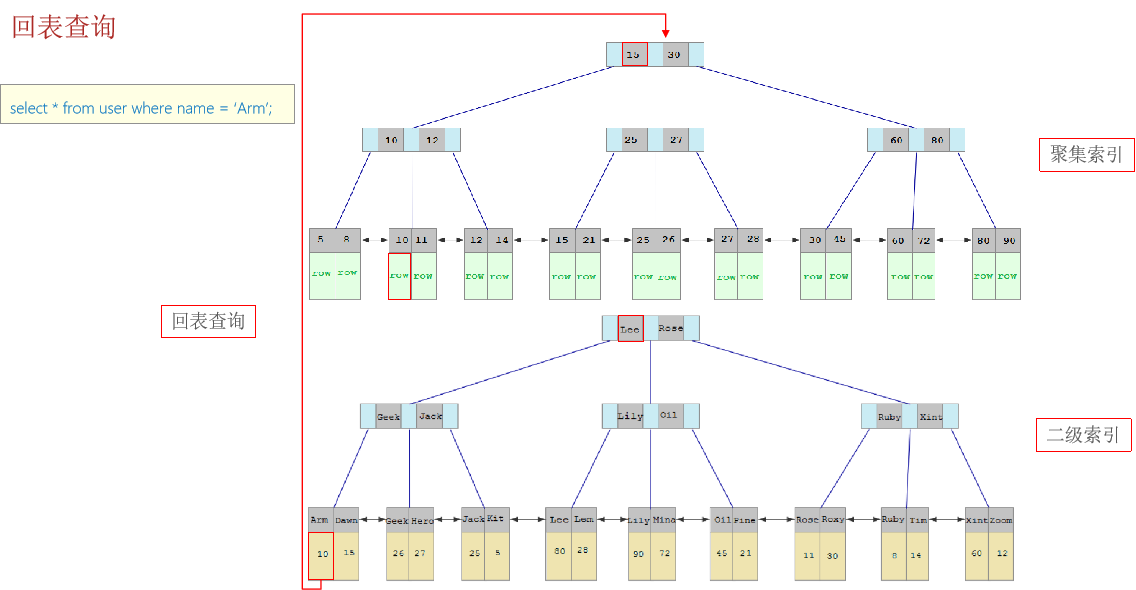
面试数据库篇(mysql)- 05什么是聚簇索引什么是非聚簇索引
聚集索引选取规则: 如果存在主键,主键索引就是聚集索引。如果不存在主键,将使用第一个唯一(UNIQUE)索引作为聚集索引。如果表没有主键,或没有合适的唯一索引,则InnoDB会自动生成一个rowid作为隐藏的聚集索…...

如何开好一家汽车美容店,汽车美容保养与装饰教学
一、教程描述 本套教程共由17张VCD组合而成,教程内容主要包括:美容店的设立和管理,汽车系统与内部结构,汽车美容工具与美容设备,美容用品的选择与使用,车身打蜡镀膜与内外清洁,车身抛光与漆面处…...

Taro + node.js 注册 仿照java 中的加盐算法
1.需求 为了让用户的密码更加保密 我们在md5 之前 在加一个随机数 用java 的说法 叫做 加盐算法 2.代码 //H5注册async H5Register(register) {if (!register.phone ||!register.password ||!register.confirmPassword ||!register.yzmCode ||!register.registerCode) {thr…...

全量知识系统问题及SmartChat给出的答复 之9 三套工具之4语法解析器 之2
Q23. 一个语言的语法简约规则 这些规则显示show 在一个给定单词(a given word)的右边或左边可能出现的单词的类别。句型的多样性variety不是复杂文法(a complex grammar)的结果,而是简单语法(a simple gra…...

简洁版用户登录系统
前端页面: 用户登录首页: <!doctype html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport"content"widthdevice-width, user-scalableno, initial-scale1.0, maximu…...

Android 监听网络状态变化
文章目录 Android 监听网络状态变化封装工具类使用 Android 监听网络状态变化 封装工具类 <uses-permission android:name"android.permission.ACCESS_NETWORK_STATE" /> <uses-permission android:name"android.permission.ACCESS_WIFI_STATE"…...

【LeetCode】一周中的第几天+ 一年中的第几天
2023-12-30 文章目录 一周中的第几天方法一:模拟思路步骤 方法二:调用库函数方法三:调用库函数 [1154. 一年中的第几天](https://leetcode.cn/problems/day-of-the-year/)方法一:直接计算思路: 方法二:调用…...
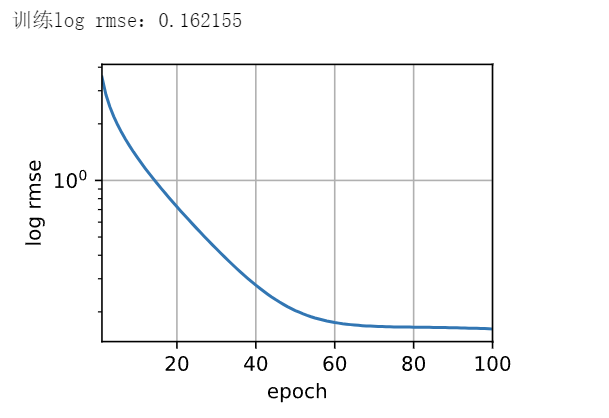
深度学习 精选笔记(10)简单案例:房价预测
学习参考: 动手学深度学习2.0Deep-Learning-with-TensorFlow-bookpytorchlightning ①如有冒犯、请联系侵删。 ②已写完的笔记文章会不定时一直修订修改(删、改、增),以达到集多方教程的精华于一文的目的。 ③非常推荐上面(学习参考&#x…...

DBGridEh 的排序
DBGridEh 可以点列抬头使得记录按该列排序 不需要写代码,只需要设置好,它就能排序。 网上的文章一般写了如何设置。但一般都少说了一条。 先说如何设置: 1. OptionsEh.AutoSortMarking 设置为 True,如果是设计期属性面板&…...
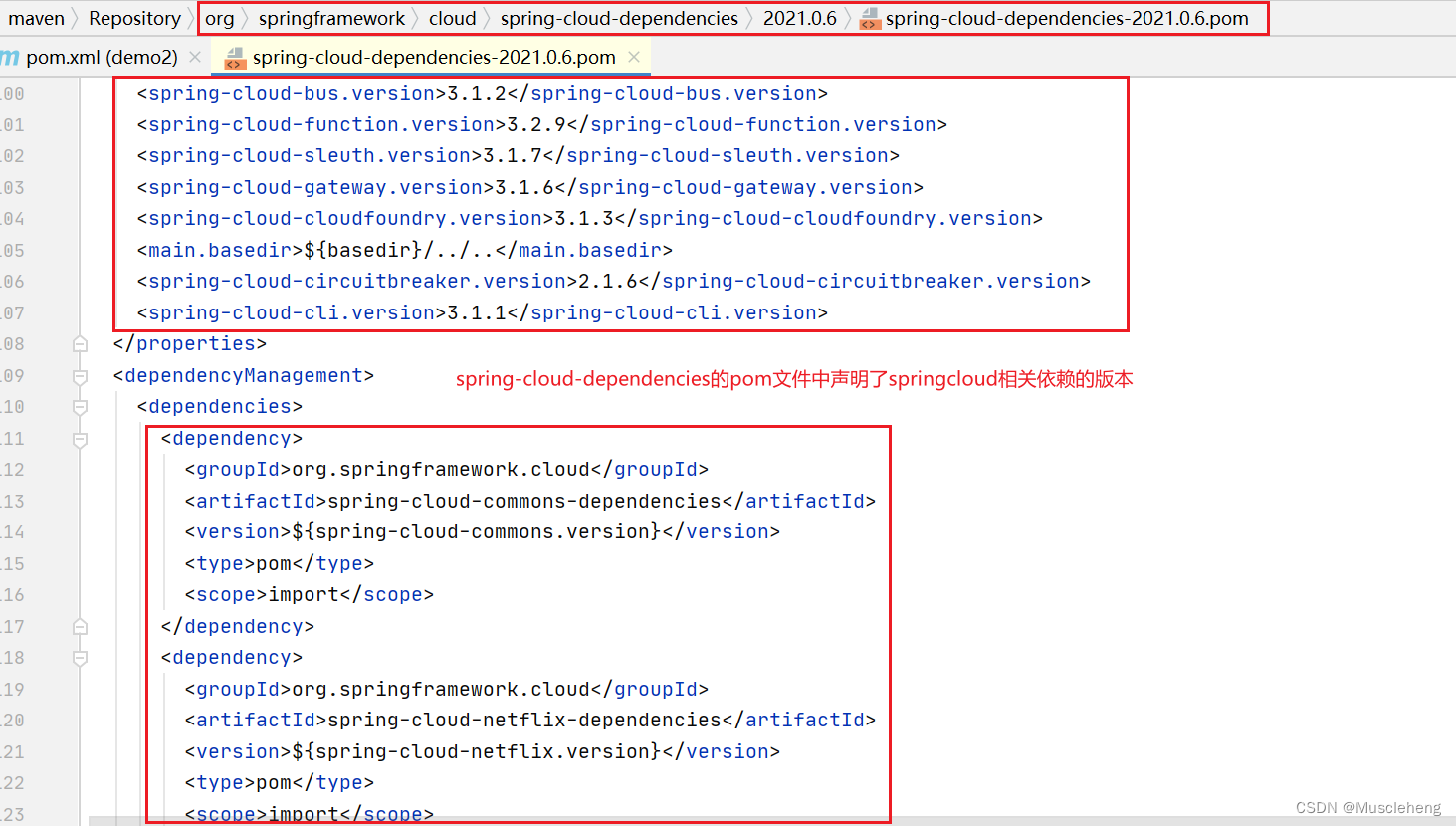
spring-boot-starter-parent和spring-boot-dependencies介绍
springboot项目的pom文件中,我们经常看见这样(下图)两种springboot的版本依赖管理方式;图片中的这两种依赖声明方式任意用其中一种都可以。文章后面会简单阐述一下区别和使用场景。 事例中完整的pom文件 <?xml version"1.0" encoding&quo…...
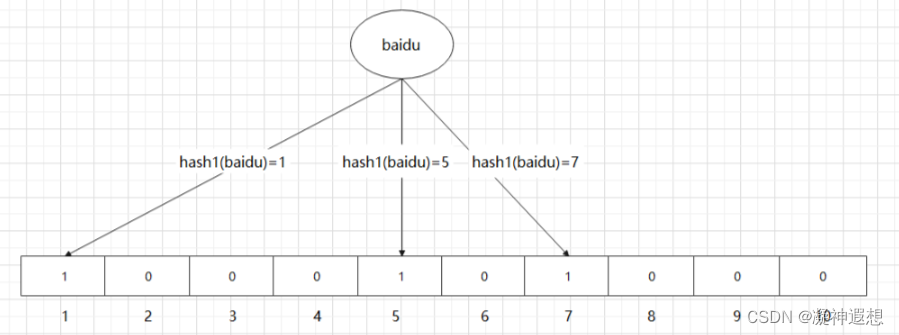
缓存穿透解决方案之布隆过滤器
布隆过滤器可以快速判断数据是否存在,避免从数据库中查询数据是否存在,减轻数据库的压力 布隆过滤器是由一个初值为0的bit数组和N个哈希函数,可以用来快速的判断某个数据是否存在 当我们想要标记某个数据是否存在时,布隆过滤器会…...

pptx和ppt有什么区别?了解两者之间的微妙差异
在现代办公和学习环境中,PowerPoint已成为我们生活中不可或缺的一部分。随着技术的不断进步,PowerPoint的格式也在不断更新。对于许多初学者,可能会对PPT和PPTX这两种格式感到困惑。本文旨在深入探讨PPTX与PPT之间的主要差异,帮助…...

LabVIEW水下温盐深数据一体化采集与分析
LabVIEW水下温盐深数据一体化采集与分析 开发一个基于LabVIEW的水下温盐深数据一体化采集与分析系统,实现海洋环境监测的自动化和精确化。通过集成温度、盐度和深度传感器,结合USB数据采集卡,利用LabVIEW软件开发的图形化界面,实…...
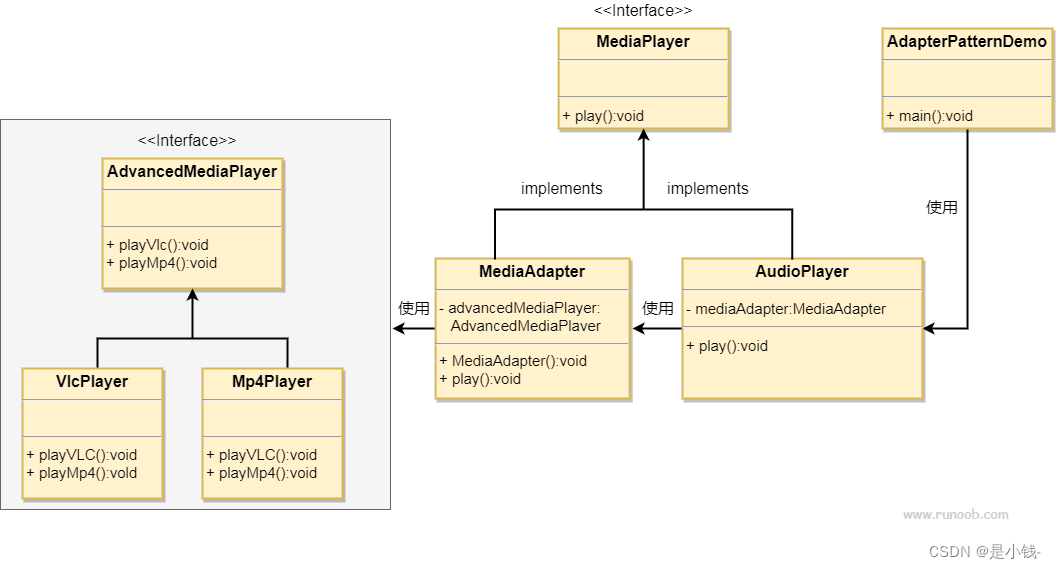
适配器模式 详解 设计模式
适配器模式 适配器模式是一种结构型设计模式,其主要作用是解决两个不兼容接口之间的兼容性问题。适配器模式通过引入一个适配器来将一个类的接口转换成客户端所期望的另一个接口,从而让原本由于接口不匹配而无法协同工作的类能够协同工作。 结构 适配…...

探索rsync远程同步和SSH免密登录的奥秘
目录 集群分发脚本xsyncscp(secure copy)安全拷贝rsync 远程同步工具集群分发脚本 SSH免密登录免密登录原理SSH免密登录配置生成公钥和私钥授权测试 在现代科技飞速发展的时代,数据的备份和迁移成为了一个重要的课题。其中,rsync远…...

JavaScript new、apply call 方法
new、apply、call、bind JavaScript 中的 apply、call和 bind 方法是前端代码开发中相当重要的概念,并且与 this 的指向密切相关 new new 关键词的主要作用 就是执行一个构造函数、返回一个实例对象 根据构造函数的情况,来确定是否可以接受参数的传递…...

助力智能化农田作物除草,基于YOLOv5全系列【n/s/m/l/x】参数模型开发构建农田作物场景下玉米苗、杂草检测识别分析系统
在我们前面的系列博文中,关于田间作物场景下的作物、杂草检测已经有过相关的开发实践了,结合智能化的设备可以实现只能除草等操作,玉米作物场景下的杂草检测我们则少有涉及,这里本文的主要目的就是想要基于DETR模型来开发构建玉米…...
转移线性dpLeetCode 2369. 检查数组是否存在有效划分)
O(1)转移线性dpLeetCode 2369. 检查数组是否存在有效划分
一、题目 1、题目描述 给你一个下标从 0 开始的整数数组 nums ,你必须将数组划分为一个或多个 连续 子数组。 如果获得的这些子数组中每个都能满足下述条件 之一 ,则可以称其为数组的一种 有效 划分: 子数组 恰 由 2 个相等元素组成…...
【力扣hot100】刷题笔记Day17
前言 今天竟然不用开组会!天大的好消息,安心刷题了 46. 全排列 - 力扣(LeetCode) 回溯(排列) class Solution:def permute(self, nums: List[int]) -> List[List[int]]:# 回溯def backtrack():if len(…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...
