Educational Codeforces Round 132 (Rated for Div. 2) E. XOR Tree(启发式合并+贪心)
题目
n(n<=2e5)个点的树,点i权值ai(1<=ai<2^30)
修改最少的点的权值,使得树上不存在异或和为0的简单路径,输出最少的点数
权值可以被修改成任意正整数(可以是无限大)
思路来源
官方题解 & zlt题解

题解
假设树形是固定的,dfs往上回溯的时候,
如果一条路径xor为0,这条路径上必须改一个值,
贪心地来看,lca必须要改
由于可以改成任意值,改lca视为把这棵子树断掉
XOR(u,v) = XOR(根到u) xor XOR(根到v) xor a[lca(u,v)]
那就是判一下某个点的子树是否存在两个点的祖先异或,等于本身的权值
这个可以启发式合并的时候,把小的集合往大的集合上挂的时候判断
删除某个点,就可以认为是清空集合
心得
自己的写法怎么写都写不对,都wa8,感觉是启发式合并公有map导致的
只能抄官方题解,每个节点维护一个set了
代码
#include<iostream>
#include<cstdio>
#include<unordered_map>
#include<set>
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,ll> P;
#define fi first
#define se second
#define pb push_back
const int N=2e5+10,INF=0x3f3f3f3f,mod=1e9+7;//998244353
int n,x,y,ans;
set<int>now[N];
int a[N],sz[N];
bool ban[N];
vector<int>E[N];
void dfs(int u,int fa,int w){bool ban=0;now[u].insert(w);for(auto &v:E[u]){if(v==fa)continue;dfs(v,u,w^a[v]);if(now[u].size()<now[v].size())now[u].swap(now[v]);for(auto &x:now[v]){if(now[u].count(x^a[u])){ban=1;break;}}for(auto &x:now[v]){now[u].insert(x);}now[v].clear();}if(ban){now[u].clear();ans++;}
}
int main(){scanf("%d",&n);for(int i=1;i<=n;++i){scanf("%d",&a[i]);}for(int i=2;i<=n;++i){scanf("%d%d",&x,&y);E[x].push_back(y);//E[i].pb(P(fa,w));E[y].push_back(x);//E[i].pb(P(fa,w));}dfs(1,0,a[1]);printf("%d\n",ans);return 0;
}相关文章:

Educational Codeforces Round 132 (Rated for Div. 2) E. XOR Tree(启发式合并+贪心)
题目 n(n<2e5)个点的树,点i权值ai(1<ai<2^30) 修改最少的点的权值,使得树上不存在异或和为0的简单路径,输出最少的点数 权值可以被修改成任意正整数(可以是无限大) 思路来源 官方…...

JavaScript 基本数据类型的详解
JavaScript的基本数据类型 以下都是JS内置的几种类型 数据类型描述number数字,不区分整数和小数string字符串类型booleantrue 真, false 假undefined表示未定义的值null只有唯一的值 null,表示空值 number 数字类型 JavaScript 中不区分整数和浮点数&…...

DDR5内存相比DDR4内存的优势和区别?选择哪一个服务器内存配置能避免丢包和延迟高?
根据幻兽帕鲁服务器的实际案例分析,选择合适的DDR4与DDR5内存大小以避免丢包和延迟高,需要考虑以下几个方面: 性能与延迟:DDR5内存相比DDR4在传输速率、带宽、工作电压等方面都有显著提升,但同时也伴随着更高的延迟。D…...

篮球游戏中的挑战精神与怄气心理:扣篮被帽后的再度冲击
在篮球比赛中,扣篮无疑是最具观赏性和震撼力的动作之一,它展示了球员的爆发力、技巧和自信。而在篮球游戏中,玩家即便面临连续扣篮被盖帽的挫折,仍渴望继续杀入内线尝试扣篮的现象,实则是体育竞技精神、挑战意识与怄气…...
JavaScript高级程序设计
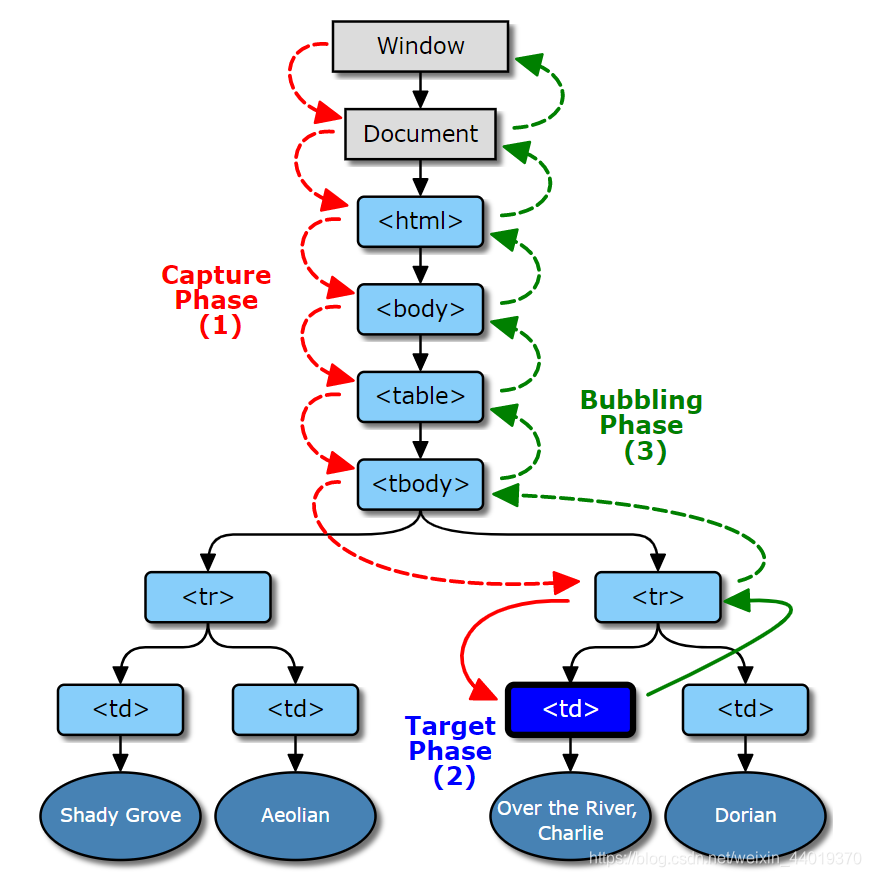
前言 《JavaScript高级程序设计》 第1章——什么是JavaScript DOM将整个页面抽象为一组分层节点。 BOM用于支持访问和操作浏览器的窗口。 第2章——HTML中的JavaScript 2.1 < script >元素 元素描述async立即开始下载脚本,但不能阻止其他页面动作&#…...

初阶数据结构:栈与队列
目录 1. 简述:栈2. 栈的功能分析与实现2.1 功能分析2.2 栈的实现2.2.1 栈的结构创建与初始化2.2.2 压栈,出栈与判空:2.2.3 获取栈顶元素,检索栈的长度与栈的销毁 3. 简述:队列4. 队列的功能分析与实现4.1 队列的功能分…...

Houdini学习笔记
按住Alt / 空格 左键:进行旋转 按住Alt / 空格 中间:移动屏幕画面 按住Alt / 空格 右键:缩放视口 如果不要Alt,就先按ESC,再去左键、中键、右键操作 这里有对应的层级关系,类似于树形结构ÿ…...
电销机器人识别客户情绪状态
最近有电销机器人需求的客户咨询我,你们OKCC的机器人可以识别客户的情绪变化吗?别人说目前电销机器人系统有支持的。 首先还是从原理的角度解答一下,是否能识别情绪状态。 是的,电销机器人可以识别客户的情绪状态。这可以通过语音…...
:2024.02.25-2024.03.01)
AI推介-大语言模型LLMs论文速览(arXiv方向):2024.02.25-2024.03.01
论文目录~ 1.Arithmetic Control of LLMs for Diverse User Preferences: Directional Preference Alignment with Multi-Objective Rewards2.Keeping LLMs Aligned After Fine-tuning: The Crucial Role of Prompt Templates3.Meta-Task Prompting Elicits Embedding from Lar…...

Cesium插件系列——3dtiles压平
本系列为自己基于cesium写的一套插件具体实现。 这里是根据Cesium提供的CustomShader来实现的。 在CustomShader的vertexShaderText里,需要定义vertexMain函数,例如下: struct VertexInput {Attributes attributes;FeatureIds featureIds;…...

APS面试审核准备的常规问题
之前根据其他人的经验贴,准备了一些可能APS 面试审核可能会遇到的常规问题,现在简单分享一下。 一般会考虑到留学资金来源,在德国能不能顺利毕业;学的是什么专业内容之类的,判断去德国会不会好好学习;对德国…...

jvm 基础知识和jvm 调优
类装载分为以下 5 个步骤: 加载:根据查找路径找到相应的 class 文件然后导入; 检查:检查加载的 class 文件的正确性; 准备:给类中的静态变量分配内存空间; 解析:虚拟机将常量池中的符…...

USB4之ASM2464PD与ASM2464PDX兼容与运用
首先在NVMe上运用: 一:ASM2464PD(现在可以做带PD的方案) 二:ASM2464PDX 1: Application Guide- CFX card reader NVMe SSD 2:ASM2464PDX Application Guide- NVMe SSD x4 with data clone 三ÿ…...

python笔记_进制
二进制 进位规则:满2进1 范围:0,1 符号:以0b和0B开头 八进制 进位规则:满8进1 范围:0-7 符号:以0o和0O开头 十进制 进位规则:满10进1 范围:0-9 十六进制 进位规则ÿ…...
面试数据库篇(mysql)- 05什么是聚簇索引什么是非聚簇索引
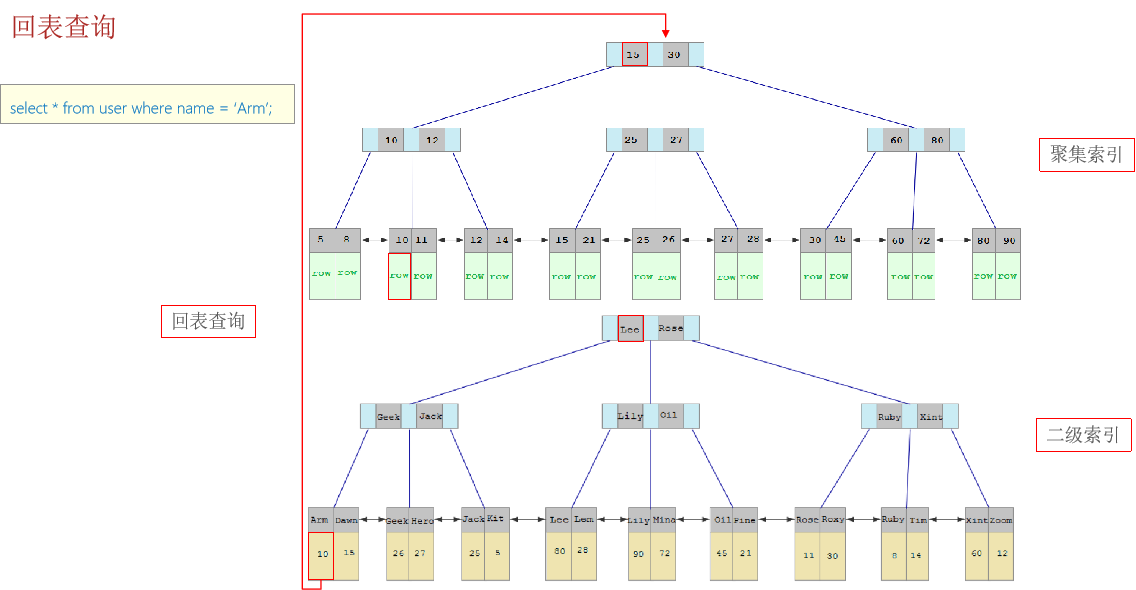
聚集索引选取规则: 如果存在主键,主键索引就是聚集索引。如果不存在主键,将使用第一个唯一(UNIQUE)索引作为聚集索引。如果表没有主键,或没有合适的唯一索引,则InnoDB会自动生成一个rowid作为隐藏的聚集索…...

如何开好一家汽车美容店,汽车美容保养与装饰教学
一、教程描述 本套教程共由17张VCD组合而成,教程内容主要包括:美容店的设立和管理,汽车系统与内部结构,汽车美容工具与美容设备,美容用品的选择与使用,车身打蜡镀膜与内外清洁,车身抛光与漆面处…...

Taro + node.js 注册 仿照java 中的加盐算法
1.需求 为了让用户的密码更加保密 我们在md5 之前 在加一个随机数 用java 的说法 叫做 加盐算法 2.代码 //H5注册async H5Register(register) {if (!register.phone ||!register.password ||!register.confirmPassword ||!register.yzmCode ||!register.registerCode) {thr…...

全量知识系统问题及SmartChat给出的答复 之9 三套工具之4语法解析器 之2
Q23. 一个语言的语法简约规则 这些规则显示show 在一个给定单词(a given word)的右边或左边可能出现的单词的类别。句型的多样性variety不是复杂文法(a complex grammar)的结果,而是简单语法(a simple gra…...

简洁版用户登录系统
前端页面: 用户登录首页: <!doctype html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport"content"widthdevice-width, user-scalableno, initial-scale1.0, maximu…...

Android 监听网络状态变化
文章目录 Android 监听网络状态变化封装工具类使用 Android 监听网络状态变化 封装工具类 <uses-permission android:name"android.permission.ACCESS_NETWORK_STATE" /> <uses-permission android:name"android.permission.ACCESS_WIFI_STATE"…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
