C++ 快速排序快速选择
目录
1、75. 颜色分类
2、912. 排序数组
3、 215. 数组中的第K个最大元素
4、LCR 159. 库存管理 III
1、75. 颜色分类

思路:利用快速排序思路,使用三指针分块进行优化。
- [0,left]——小于key
- [left+1,right-1]——等于key
- [right,nums.size()]——大于key
class Solution {
public:void sortColors(vector<int>& nums) {int n = nums.size();int left = -1, right = n, cur = 0;while (cur < right) {if (nums[cur] == 0)swap(nums[++left], nums[cur++]);else if (nums[cur] == 2)swap(nums[--right], nums[cur]);elsecur++;}}
};2、912. 排序数组

思路:快排+三指针优化+随机选择基准元素
class Solution {
public:vector<int> sortArray(vector<int>& nums) {srand(time(NULL));qsort(nums,0,nums.size()-1);return nums;}int getRandom(vector<int>& nums,int left,int right){int i=rand();return nums[i%(right-left+1)+left];}void qsort(vector<int>& nums,int begin,int end){if(begin >= end)return;int i=begin,left=begin-1,right=end+1;int key=getRandom(nums,begin,end);while(i<right){if(nums[i]<key)swap(nums[++left],nums[i++]);else if(nums[i]>key)swap(nums[--right],nums[i]);elsei++;}qsort(nums,begin,left);qsort(nums,right,end);}
};3、 215. 数组中的第K个最大元素

思路:快速选择(快排+三指针分块+随机选择基准元素+递归排序时进入对应区间)
- 第k个最大元素也就是排序(升序)后的倒数第k个
<key =key >key
|————|————————|—————|l left left+1 right-1 right r
a b c(区间元素个数)
c表示在当前key(基准值)右侧的元素数量(即比key大的元素数量),b表示等于key的元素数量。由于我们是寻找第k个最大的元素,数组的右侧代表了较大的元素。
if (c >= k):如果key右侧的元素数量c大于或等于k,这意味着第k个最大的元素位于key的右侧或者是key本身。因此,我们递归地在key右侧的数组部分继续进行快速选择,寻找第k个最大的元素。
else if (b + c >= k):如果key右侧的元素数量c加上等于key的元素数量b大于或等于k,这意味着第k个最大的元素要么是key本身,要么在等于key的这些元素中。由于这些元素都是相等的,我们可以直接返回key作为第k个最大的元素。
else:如果上述两个条件都不满足,这意味着第k个最大的元素位于key的左侧。因此,我们递归地在pivot左侧的数组部分继续进行快速选择。此时,我们需要调整k的值,因为我们已经排除了b + c个比key大或等于key的元素,所以新的k应该减去这部分已经排除的元素数量。
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));return qsort(nums, 0, nums.size() - 1, k);}int qsort(vector<int>& nums, int l, int r, int k) {if (l == r)return nums[l];int key = getRandom(nums, l, r);int left = l - 1, right = r + 1, i = l;while (i < right) {if (nums[i] < key)swap(nums[++left], nums[i++]);else if (nums[i] > key)swap(nums[--right], nums[i]);elsei++;}int c = r - right + 1, b = right - left - 1;if (c >= k)return qsort(nums, right, r, k);else if (b + c >= k)return key;elsereturn qsort(nums, l, left, k - b - c);}int getRandom(vector<int>& nums, int left, int right) {return nums[rand() % (right - left + 1) + left];}
};为了找到数组中第k个最大的元素,并且要求时间复杂度为O(n),我们可以比较这些方法:
-
快速选择算法(第一种方法):
- 优点: 平均时间复杂度为O(n),符合题目要求。它通过随机选择一个枢轴来分割数组,然后只在包含第k个最大元素的那部分数组上递归,从而减少了不必要的计算。
- 缺点: 最坏情况下的时间复杂度为O(n^2),但这种情况很少发生。算法的性能依赖于随机数的选择。
-
最小堆(第二种方法):
- 优点: 对于找到第k个最大元素,这种方法维护了一个大小为k的最小堆,时间复杂度为O(n log k),适合k远小于n的情况。
- 缺点: 当k接近n时,性能不如快速选择算法。
class Solution { public:int findKthLargest(vector<int>& nums, int k) {priority_queue<int,vector<int>,greater<int>> pq(nums.begin(),nums.begin()+k);for(size_t i=k;i<nums.size();i++){if(nums[i]>pq.top()){pq.pop();pq.push(nums[i]);}}return pq.top();} };
-
排序(第三种方法):
- 优点: 实现简单,直观易懂。
- 缺点: 时间复杂度为O(n log n),不满足题目对O(n)时间复杂度的要求。
class Solution { public:int findKthLargest(vector<int>& nums, int k) {sort(nums.begin(),nums.end());return nums[nums.size()-k];} };
-
最大堆(第四种方法):
- 优点: 通过构建一个最大堆,然后弹出k-1次,可以直接得到第k个最大元素。这种方法简单且对于理解堆结构很有帮助。
- 缺点: 时间复杂度为O(n + k log n),当k较小相对高效,但当k接近n时,性能下降。
class Solution { public:int findKthLargest(vector<int>& nums, int k) {priority_queue<int> pq(nums.begin(),nums.end());while(--k){pq.pop();}return pq.top();} };
结论:
- 如果你追求平均情况下的最优时间复杂度,并且可以接受在极少数情况下性能的不确定性,快速选择算法是最佳选择。
- 如果k值较小,最小堆方法也是一个不错的选择,因为它可以较快地找到第k个最大的元素。
- 排序方法虽然简单,但不满足题目对时间复杂度的要求。
- 最大堆方法适用于k值较小的情况,但当k值较大时,性能不是最优的。
综上所述,考虑到时间复杂度的要求和算法的效率,快速选择算法是最符合题目要求的解决方案
4、LCR 159. 库存管理 III

思路:快速选择(快排+三指针分块+随机选择基准元素+进入对应区间寻找)
<key =key >key
|————|————————|—————|l left left+1 right-1 right r
a b c(区间元素个数)
a表示在当前的key(基准值)左边的元素数量,b表示等于key的元素数量。cnt是我们需要找到的库存余量最少的商品数量。
if (a > cnt):如果key左边的元素数量a大于cnt,这意味着我们需要的cnt个最小元素全部位于key的左边。因此,我们递归地在key左边的数组部分继续进行快速选择,寻找这cnt个最小元素。
else if (a + b >= cnt):如果key左边的元素数量a加上等于key的元素数量b大于或等于cnt,这意味着我们需要的cnt个最小元素已经包含在左边的元素和等于key的元素中。由于题目说明返回顺序不限,我们不需要进一步排序或选择,可以直接返回结果。
else:如果上述两个条件都不满足,这意味着我们需要的cnt个最小元素部分位于key的右边。因此,我们递归地在key右边的数组部分继续进行快速选择。此时,我们需要调整cnt的值,因为我们已经找到了一部分所需的最小元素(即a + b个),所以新的cnt应该减去这部分已经找到的元素数量。
class Solution {
public:vector<int> inventoryManagement(vector<int>& stock, int cnt) {srand(time(NULL));qsort(stock, 0, stock.size() - 1, cnt);return {stock.begin(), stock.begin() + cnt};}int qsort(vector<int>& stock, int l, int r, int cnt) {if (l == r)return stock[l];int key = getRandom(stock, l, r);int left = l - 1, right = r + 1, i = l;while (i < right) {if (stock[i] < key)swap(stock[++left], stock[i++]);else if (stock[i] > key)swap(stock[--right], stock[i]);elsei++;}int a = left - l + 1, b = right - left - 1;if (a > cnt)return qsort(stock, l, left, cnt);else if (a + b >= cnt)return 0;elsereturn qsort(stock, right, r, cnt - b - a);}int getRandom(vector<int>& stock, int left, int right) {return stock[rand() % (right - left + 1) + left];}
};相关文章:

C++ 快速排序快速选择
目录 1、75. 颜色分类 2、912. 排序数组 3、 215. 数组中的第K个最大元素 4、LCR 159. 库存管理 III 1、75. 颜色分类 思路:利用快速排序思路,使用三指针分块进行优化。 [0,left]——小于key[left1,right-1]——等于key[right,nums.size()]——大于k…...
雅马哈伺服器TS-S系列说明具体详情内容可参看PDF目录内容
雅马哈伺服器TS-S系列说明具体详情内容可参看PDF目录内容...
SpringBoot底层原理
SpringBoot底层原理 一 配置优先级 1.配置方式 Springboot中支持三种配置方式,分别为: application.propertiesapplication.ymlapplication.yaml 2.配置优先级 当存在多份配置文件时,配置文件会按照它们的优先级生效。 优先级从高到底…...
【golang】25、图片操作
用 “github.com/fogleman/gg” 可以画线, 框 用 “github.com/disintegration/imaging” 可以变换颜色 一、渲染 1.1 框和字 import "github.com/fogleman/gg"func DrawRectangles(inPath string, cRects []ColorTextRect, fnImgNameChange FnImgNameChange) (st…...
kswapd0挖矿病毒攻击记录
文章目录 一、起因与病毒分析1、起因2、阿里云告警2.1 恶意脚本代码执行12.2 恶意脚本代码执行22.3恶意脚本代码执行32.4 恶意脚本代码执行4 3、病毒简单分析3.1 病毒的初始化3.2 病毒本体执行 4、总结 二、ubuntu自救指南1、病毒清理2、如何防御 一、起因与病毒分析 1、起因 …...

如何使用 takeUntil RxJS 操作符来声明性地管理订阅
简介 Angular 处理取消订阅可观察对象的操作,比如从 HTTP 服务返回的可观察对象或者使用 async 管道时。然而,对于其他情况,管理所有订阅并确保取消长期存在的订阅可能会变得困难。而且,取消大部分订阅的策略也会带来自己的问题。…...
在Centos中用Docker部署oracle-12c
一、介绍 Oracle 12c是Oracle 11g的后续版本。12c代表云计算(Cloud Computing),这是Oracle在该版本中强调的一个关键概念。它具有多租户架构、数据库内存、安全增强、大数据管理和自动化管理等功能。它被广泛应用于企业级应用程序和大型数据…...

JS进阶——高级技巧
版权声明 本文章来源于B站上的某马课程,由本人整理,仅供学习交流使用。如涉及侵权问题,请立即与本人联系,本人将积极配合删除相关内容。感谢理解和支持,本人致力于维护原创作品的权益,共同营造一个尊重知识…...

TG-ADMIN 权限管理系统
项目简介 该项目是一款基于 SpringBoot + Vue2 + Jwt + ElementUi的 RBAC模型管理系统。 主要以自定义拦截器和jwt结合进行权限验证 通过自定义指令实现按钮级别权限,使用经典的RBAC模型 什么是RBAC? 1、RBAC模型概述 RBAC模型(Role-Based Access Control:基于角色的…...
)
十五届蓝桥杯第三期模拟赛题单(C++、java、Python)
备战2024年蓝桥杯 省赛第三期模拟赛题单 备战Python大学A组 第一题 【问题描述】 请问 2023 有多少个约数?即有多少个正整数,使得 2023 是这个正整数的整数倍。 【问题描述】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果…...

嵌入式驱动学习第一周——git的使用
前言 本文主要介绍git的使用,包括介绍git,gitee,以及使用gitee创建仓库并托管代码 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程,未来预计四个月将高强度更新本专栏,喜欢的可以关注本博主并订阅本专栏…...
界面控件DevExpress .NET MAUI v23.2新版亮点 - 拥有全新的彩色主题
DevExpress拥有.NET开发需要的所有平台控件,包含600多个UI控件、报表平台、DevExpress Dashboard eXpressApp 框架、适用于 Visual Studio的CodeRush等一系列辅助工具。屡获大奖的软件开发平台DevExpress 今年第一个重要版本v23.1正式发布,该版本拥有众多…...
的意义)
大语言模型LLM Pro+中Pro+(Prompting)的意义
—— Pro ,即Prompting,构造提示 1.LLM Pro中Pro(Prompting)的意义 Prompting不仅是大语言模型交互和调用的一种高效手段,而且已成为推动模型泛化能力和应用灵活性的关键技术路径,它不仅极大地拓展了模型功…...

React 中,children 属性
在 React 中,children 属性是一个特殊的属性,它允许你将组件作为其他组件的子元素传递。这意味着你可以在组件内部嵌套任何类型的子组件或元素,并且在父组件中通过 props.children 访问它们。这为组件的复用和组合提供了极大的灵活性。 以下…...

多行业万能预约门店小程序源码系统 支持多门店预约小程序 带完整的安装代码包以及搭建教程
随着消费者对于服务体验要求的不断提升,门店预约系统成为了许多行业提升服务质量、提高运营效率的重要工具。然而,市面上的预约系统往往功能单一,无法满足多行业、多场景的个性化需求。下面,小编集合了多年的行业经验和技术积累&a…...

Node.js 中 fs 模块文件操作的应用教程
Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境,它可以让 JavaScript 代码在服务器端运行。在 Node.js 中,fs 模块是用来处理文件系统操作的模块。通过 fs 模块,我们可以进行文件的读取、写入、删除等操作。本教程将介绍如何在 No…...

一些常用到的git命令
git stash -a //缓存所有文件 git checkout -b dev origin/dev //切换到dev分支上,接着跟远程的origin地址上的dev分支关联起来 //推送本地分支到远程仓库 git push origin localbranchname:remotebrancname git revert onefile //https://www.freecodecamp.org/news/git-re…...

spring boot3解决跨域的几种方式
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途。 目录 1.前言 2.何为跨域 3.跨域问题出现特征 4.方式一:使用 CrossOrigin 注解 5.方式二:自定义…...

【Spring】19 @Autowired注解使用详解
文章目录 构造函数注入Setter方法注入字段注入数组和集合注入特殊情况处理特殊接口类型的注入异常处理结语 Spring 框架的 Autowired 注解是实现依赖注入的一种强大而灵活的方式。在本文中,我们将介绍 Autowired 注解的多种用法,包括构造函数、setter方法…...

Educational Codeforces Round 132 (Rated for Div. 2) E. XOR Tree(启发式合并+贪心)
题目 n(n<2e5)个点的树,点i权值ai(1<ai<2^30) 修改最少的点的权值,使得树上不存在异或和为0的简单路径,输出最少的点数 权值可以被修改成任意正整数(可以是无限大) 思路来源 官方…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...
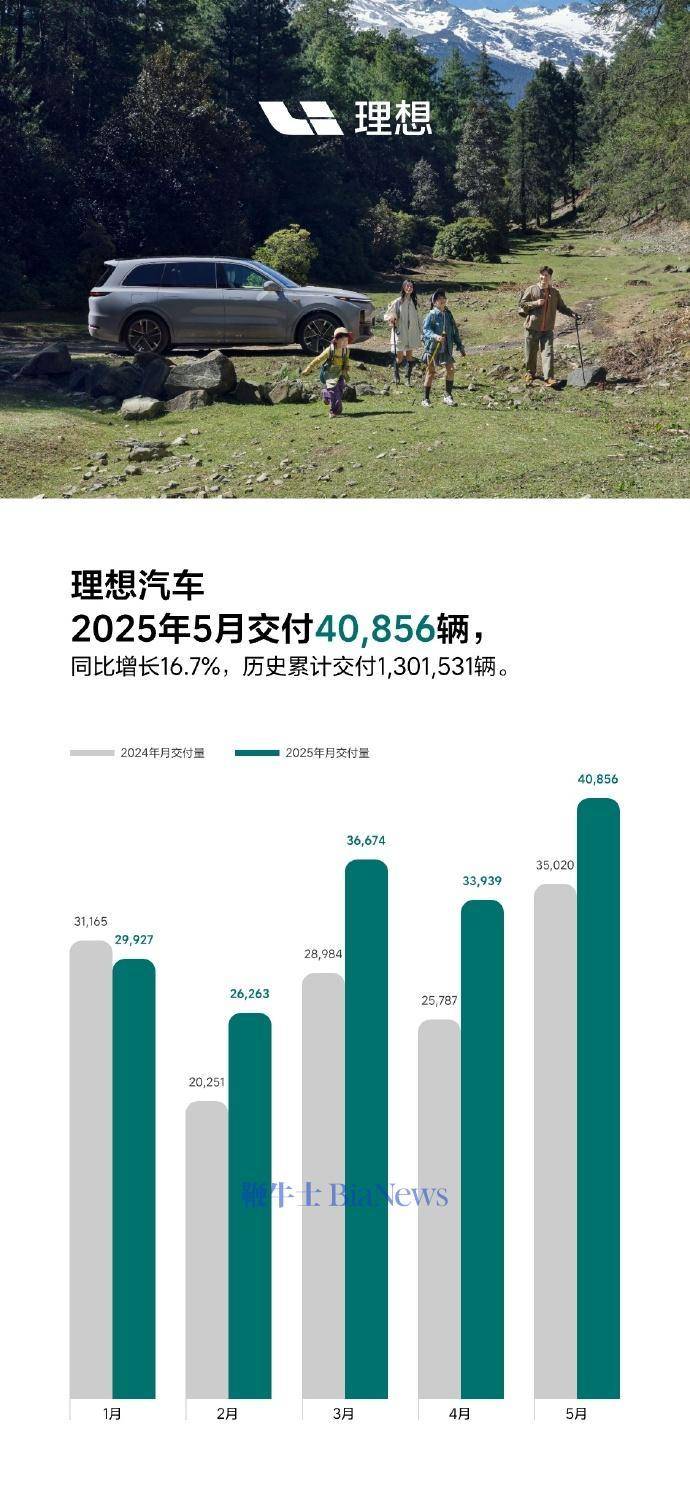
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
