机器人与AGI会撞出什么火花?
真正的科技变革是不是就要来临了?各方大佬都开始布局机器人,对于普通人的就业会造成什么影响?

优牛企讯-企业动态信息监控专家
在优牛企讯-企业动态监控专家搜索可知,全国目前的机器人公司已经达到了26401家,近一年内注册的就达到了3000多家,这些企业的诞生会增加还是减少职位呢?
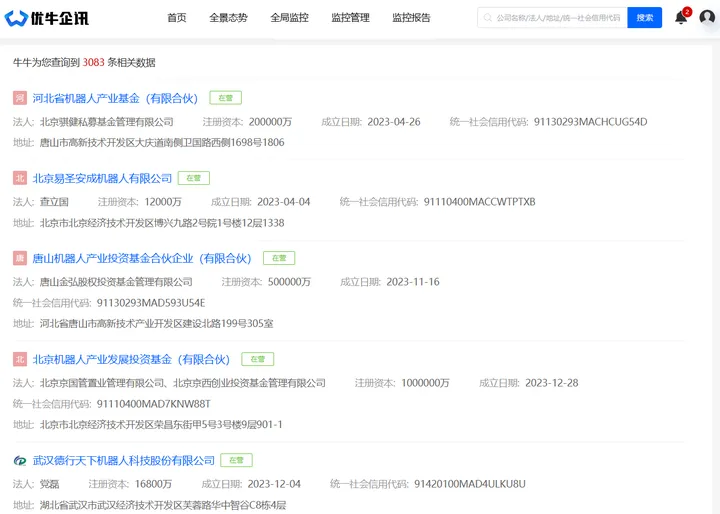
优牛企讯-企业动态信息监控专家
我们需要了解什么是人工通用智能(AGI)。AGI是指一种具有广泛认知能力的人工智能,能够在各种不同的任务和环境中表现出与人类相似的智能水平。与目前大多数人工智能系统不同,AGI不仅限于执行特定任务,而是能够像人类一样解决各种问题、学习和适应新环境。
当各方大佬开始布局机器人领域时,他们的目标不仅仅是制造出能够执行简单任务的机器人。他们将目光投向了AGI,希望通过将其与机器人结合,创造出具有高度自主性和智能的机器人系统。这种结合将激发出许多火花,为我们的生活带来更多便利和创新。
一方面,结合AGI的机器人将在工业制造领域展现出巨大的潜力。它们可以自主地完成复杂的生产线任务,提高工作效率和质量。此外,它们还能够实时监测和分析生产过程中的数据,帮助优化生产流程,减少浪费和成本。这将极大地推动制造业的升级和转型。
另一方面,结合AGI的机器人也将在服务行业发挥重要作用。例如,它们可以在医疗领域提供个性化的护理和监护服务,帮助照顾老年人和残疾人士。在教育领域,它们可以作为智能教师,根据学生的需求和能力进行个性化教学。此外,它们还可以在家庭中担任智能家居助手,提供各种生活帮助和娱乐功能。
结合AGI的机器人也带来了一些挑战和争议。其中之一是关于隐私和安全的问题。这些机器人将收集和处理大量的个人数据,包括我们的生活习惯、健康状况等。如何保护这些数据的安全和隐私,防止滥用和泄露,将是一个重要的议题。
人们还担心结合AGI的机器人可能会取代人类的工作岗位。虽然机器人可以提高生产效率,但也可能导致部分人力岗位的减少。因此,我们需要思考如何平衡机器人的发展和人类的就业问题,确保机器人的应用不会对社会造成不利影响。
这个时代何时到来?能否预测?这是一个复杂的问题。尽管科技发展迅速,但要实现AGI仍然面临许多技术难题和伦理挑战。目前,我们还无法确定具体的时间点。然而,随着各方大佬的积极布局和技术的不断进步,我们可以期待这个时代的到来,并为之做好准备。
相关文章:

机器人与AGI会撞出什么火花?
真正的科技变革是不是就要来临了?各方大佬都开始布局机器人,对于普通人的就业会造成什么影响? 优牛企讯-企业动态信息监控专家 在优牛企讯-企业动态监控专家搜索可知,全国目前的机器人公司已经达到了26401家,近一年…...
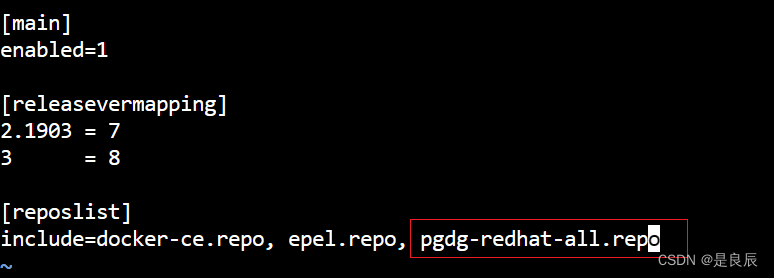
Linux yum安装pgsql出现Bad GPG signature错误
官方文档:https://www.postgresql.org/download/linux/redhat/ sudo yum install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-7-x86_64/pgdg-redhat-repo-latest.noarch.rpm sudo yum install -y postgresql12-server sudo /usr/pgsql-12/bin/…...
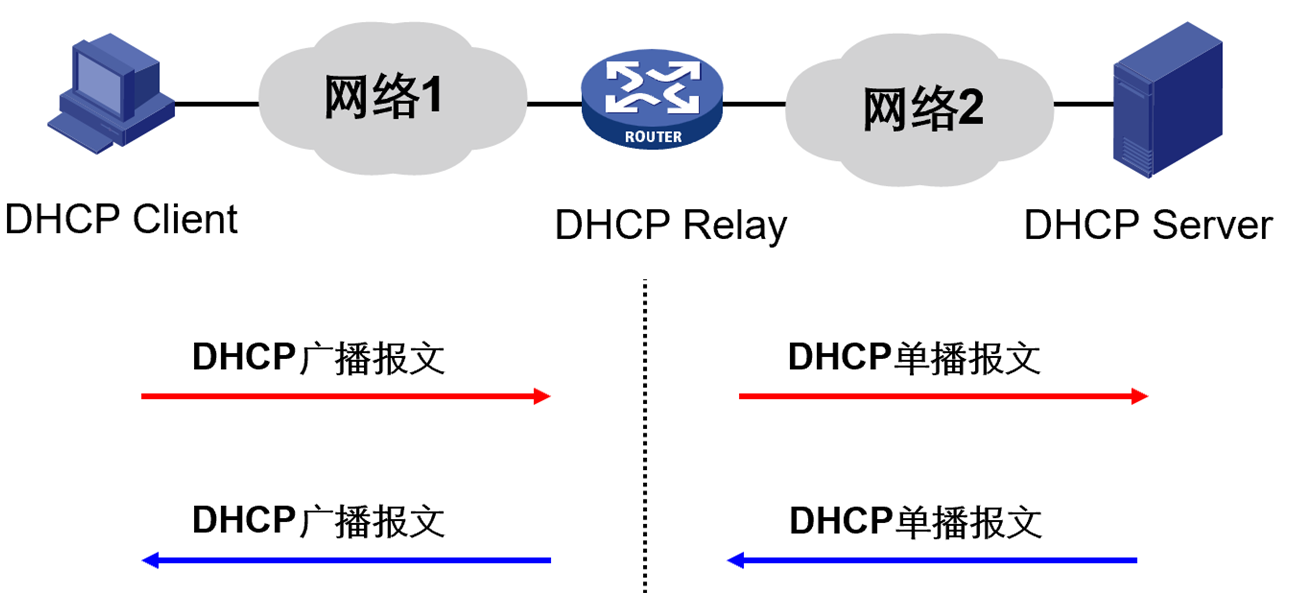
第18章-DHCP
1. 产生背景 2. 概述 2.1 定义 2.2 特点 2.3 DHCP系统组成 3. DHCP工作原理 3.1 前提条件 3.2 场景 3.3 分配IP地址工作机制 3.4 特殊情况处理 3.5 IP地址租约更新 4. DHCP中继代理 4.1 现实场景 4.2 工作机制 1. 产生背景 现实问题: 小型网络中&…...
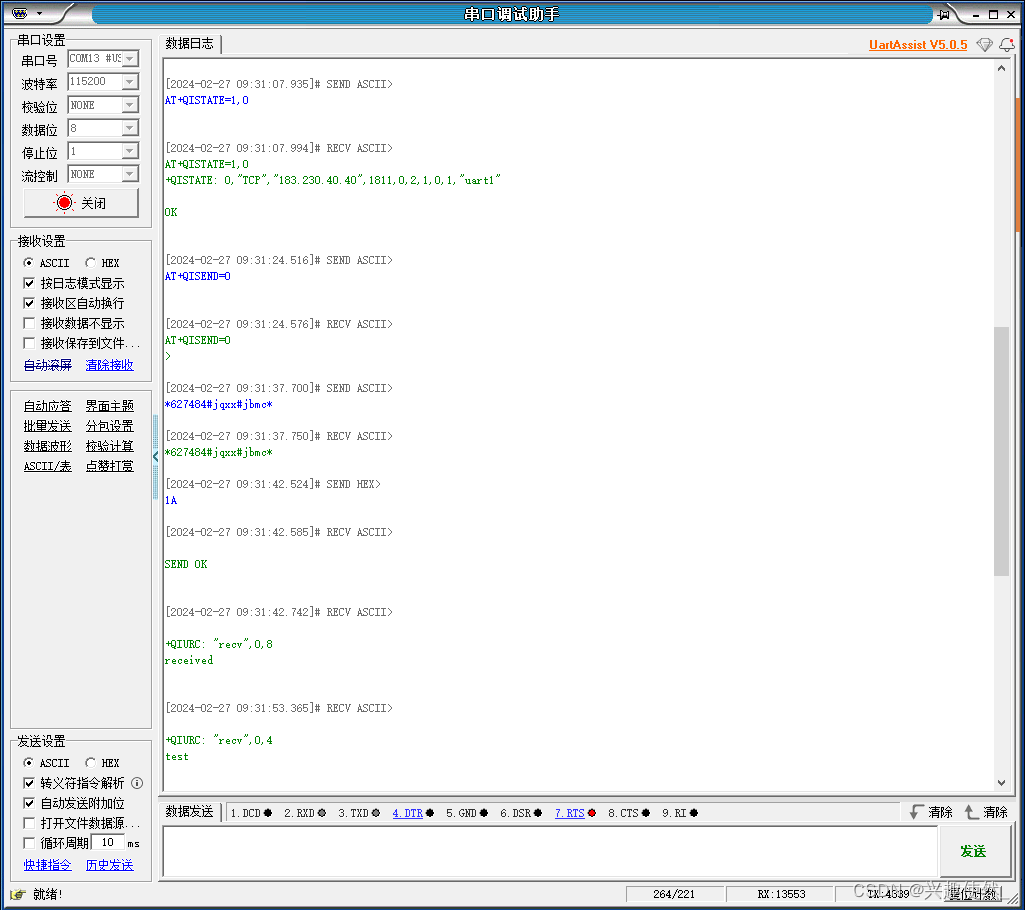
[物联网] OneNet 多协议TCP透传
[物联网] OneNet 多协议TCP透传 STM32物联网–ONENET云平台的多协议接入产品创建 : https://blog.csdn.net/qq_44942724/article/details/134492924 Onenet tcp 透传 : https://blog.csdn.net/flyme2010/article/details/107086001 tcp服务端测试工具 : http://tcp.xnkiot.com/…...
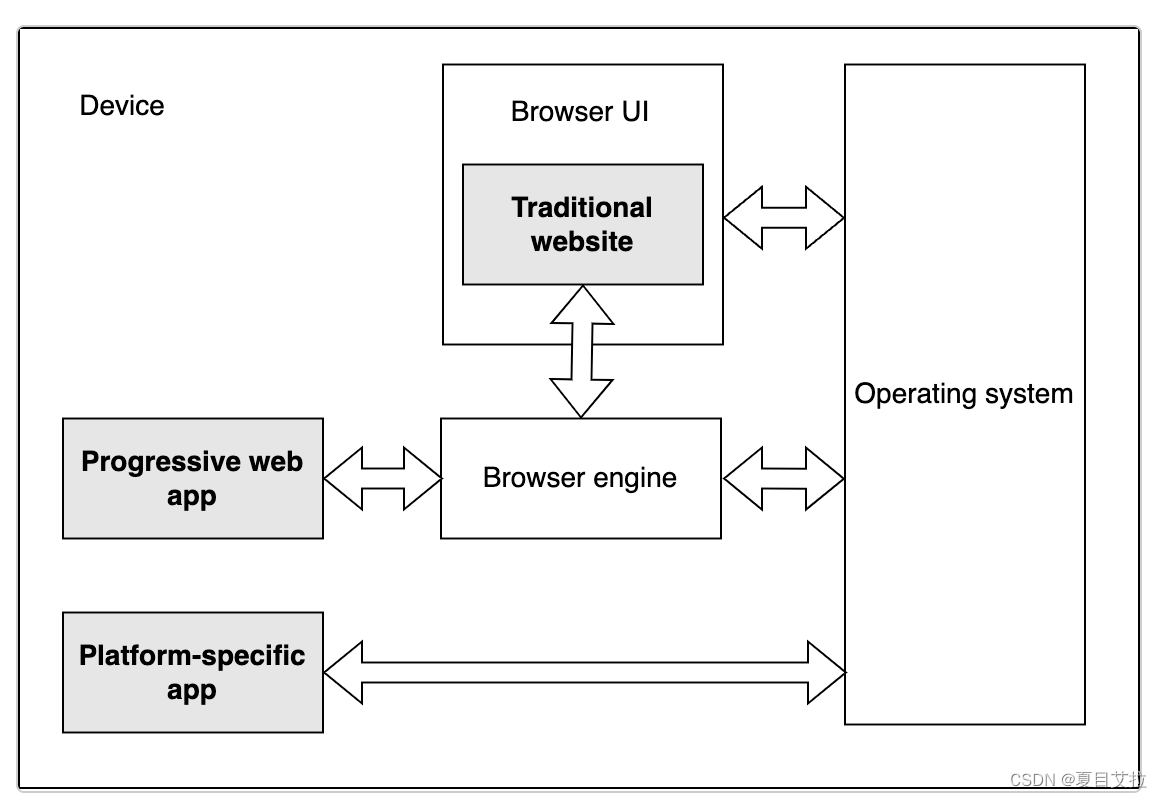
如何让网页APP化 渐进式Web应用(PWA)
前言 大家上网应该发现有的网页说可以安装对应应用,结果这个应用好像就是个web,不像是应用,因为这里采用了PWA相关技术。 PWA,全称为渐进式Web应用(Progressive Web Apps),是一种可以提供类似…...
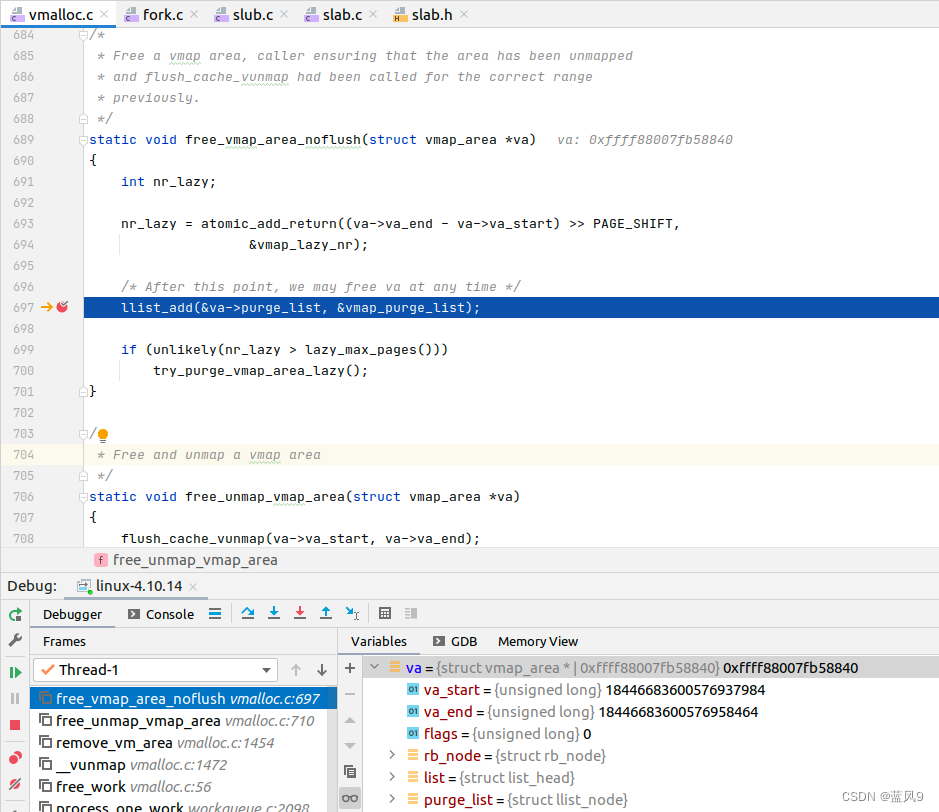
50 vmalloc 的实现
前言 这里说的是 内核中分配按页分配的场景 常用于 驱动什么的, 分配 中大型空间 由于 连续的 n 个页是分别使用 alloc_pages 分配的, 因此是 虚拟地址空间连续, 但是 物理地址空间不连续 如何分配对象 两个步骤, __get_vm_area_node 获取为 size 分配的 vma 区间, 然后…...

程序员的金三银四求职宝典!
目录 编辑 程序员的金三银四求职宝典 一、为什么金三银四是程序员求职的黄金时期? 二、如何准备金三银四求职? 1. 完善简历 2. 增强技术能力 3. 提前考虑目标公司 4. 提前准备面试 三、程序员求职的常见面试题 1. 数据结构和算法 2. 数据库 …...
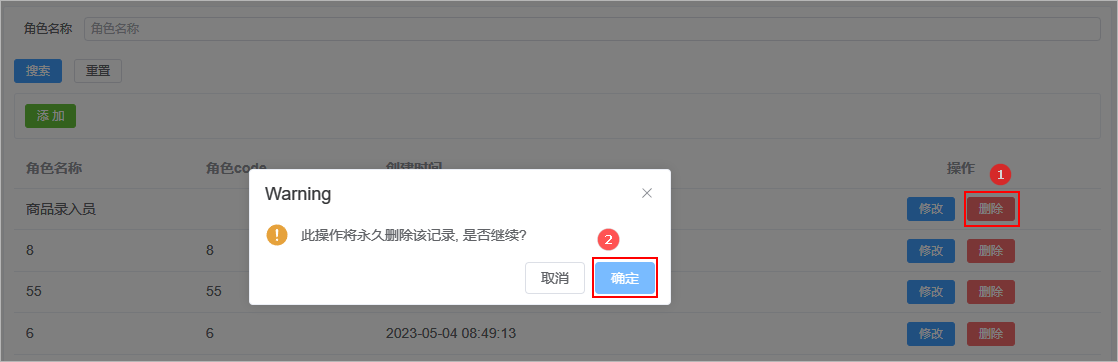
day04_拦截器Apifox角色管理(登录校验,API接口文档,权限管理说明,角色管理,添加角色,修改角色,删除角色)
文章目录 1. 登录校验1.1 需求说明1.2 实现思路1.3 ThreadLocal1.4 AuthContextUtil1.5 拦截器使用1.5.1 拦截器开发1.5.2 拦截器注册 1.6 代码优化1.6.1 配置优化1.6.2 代码优化1.6.3 前端修改 2. API接口文档2.1 Apifox接口管理平台2.1.1 接口管理平台简介2.1.2 Apifox简介2.…...
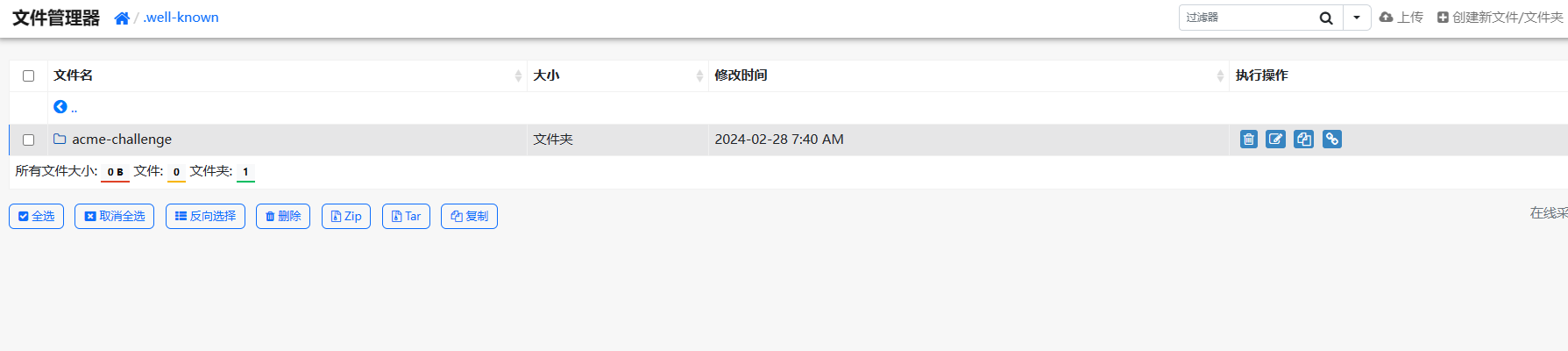
在线上传解压PHP文件代码,压缩/压缩(网站一键打包)支持密码登录
在线上传解压PHP文件代码,压缩/压缩(网站一键打包)支持密码登录 资源宝分享:www.httple.net 如果你没有主机控制面板这个是最好选择,不需要数据库,上传当控制面板使用,无需安装任何扩展,安全高,…...

【刷题】模拟
模拟算法:题目中已经告诉应该怎么做了,只需要模拟即可,思路比较简单,比较考察代码能力。 一般先在草稿纸上模拟流程,如果直接写代码,容易忽视细节,并且不容器调试! 优化策略&#…...
【打工日常】使用docker部署在线Photopea用于linux下替代ps
一、Photopea介绍 linux没有ps适配,对于有时候工作来说确实不方便,我找了很久,才找到了一款功能可以跟ps接近的在线软件,使用docker部署就可以了。它是ps的最佳替代品之一,其界面几乎与ps相同,只不过它是在…...
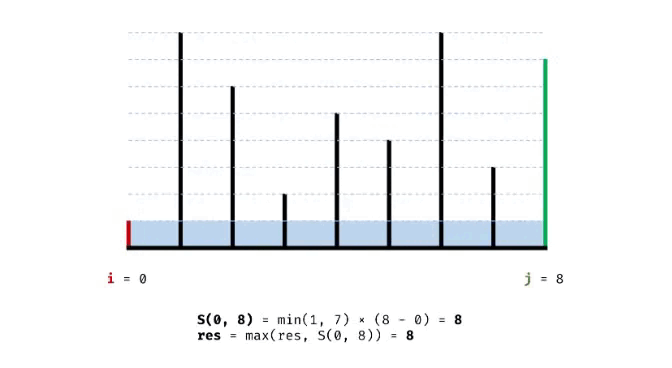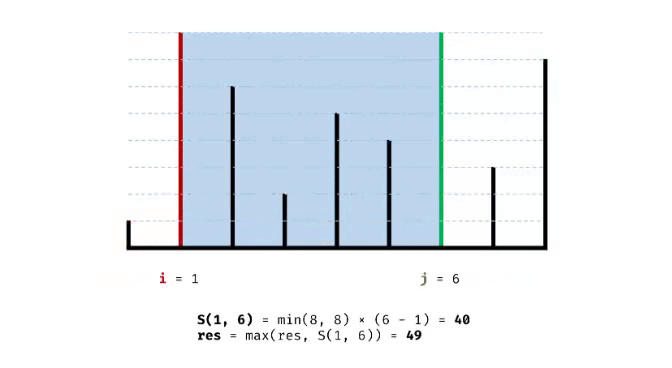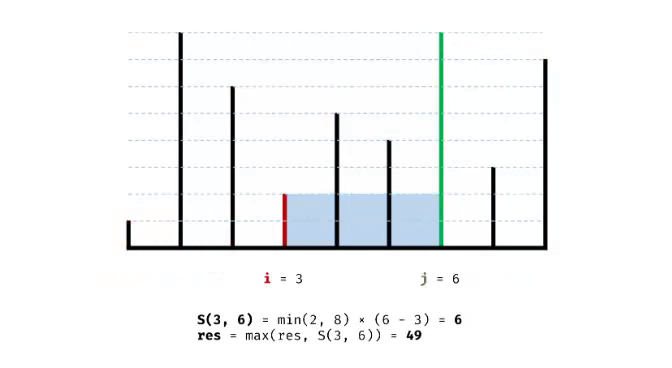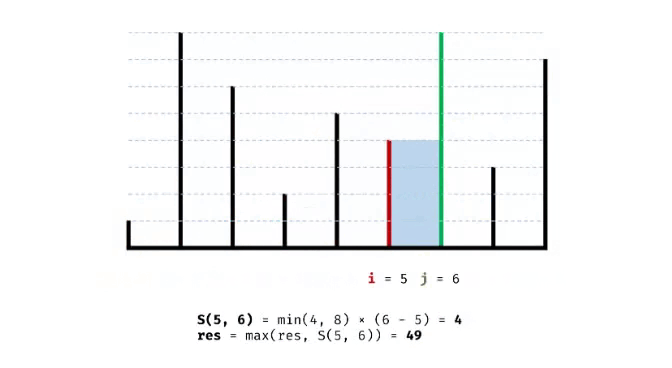
leetcode 热题 100_盛最多水的容器
题解一: 双指针遍历:容量计算公式为min(左高度,右高度)*底部距离,我们可以令底部距离逐步递减(左右两边的指针向中部移动)。此时对于min(左高度,右高度),假设较高的线向中部移动&…...

基本正则表达式
基本正则表达式 正则命令功能^尖角号,用于模式的最左侧,如“^oldbpy",匹配以oldboy单词开头的行$美元符,用于模式的最右侧,如"oldboy$",表示以oldboy单词结尾的行^$组合符&…...

sqlserver保存微信Emoji表情
首先将数据库字段,设置类型为 nvarchar(200)一个emoji表情,占4字节就可以了,web前端展示不用改任何东西,直接提交数据保存;回显也会没有问题,C#代码不用做任何处理; 不哭不闹要睡觉ἱ…...
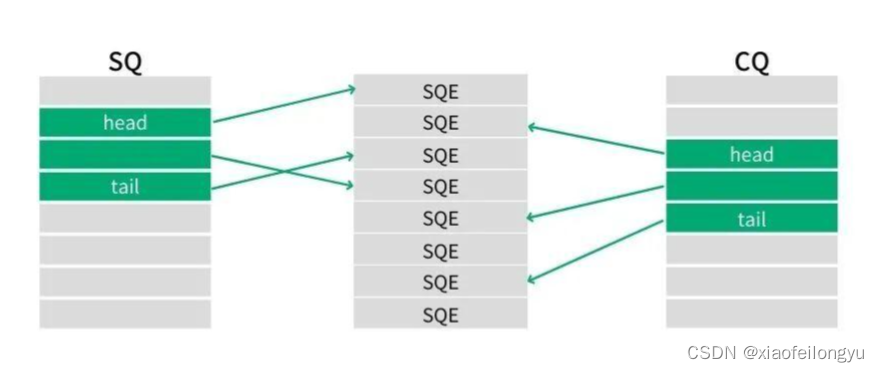
网络编程 io_uring
io_uring 1、概述 io_uring是Linux(内核版本在5.1以后)在2019年加入到内核中的一种新型的异步I/O模型; io_uring使用共享内存,解决高IOPS场景中的用户态和内核态的切换过程,减少系统调用;用户可以直接向…...

Java中的static
Java中的static 同一个类的静态变量共享同一个内存空间,即静态变量也就是被 static 关键字修饰的变量。它可以被类的所有实例共享,无论一个类创建了多少个对象,它们都共享同一份静态变量。从变量在内存中的存储方式来看,如果成员…...
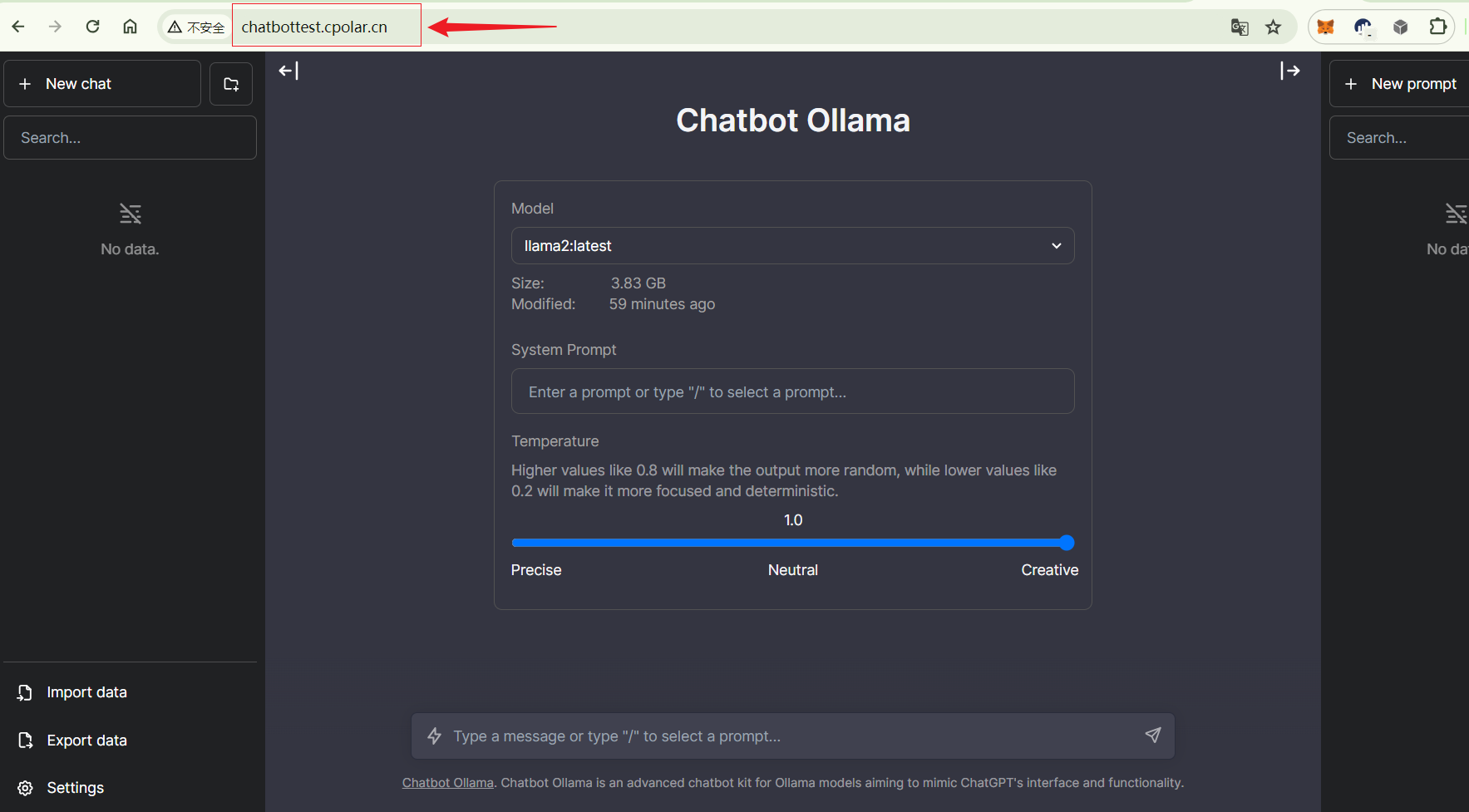
如何在群晖Docker运行本地聊天机器人并结合内网穿透发布到公网访问
文章目录 1. 拉取相关的Docker镜像2. 运行Ollama 镜像3. 运行Chatbot Ollama镜像4. 本地访问5. 群晖安装Cpolar6. 配置公网地址7. 公网访问8. 固定公网地址 随着ChatGPT 和open Sora 的热度剧增,大语言模型时代,开启了AI新篇章,大语言模型的应用非常广泛,包括聊天机…...
lv20 QT进程线程编程
知识点:启动进程 ,线程 ,线程同步互斥 1 启动进程 应用场景:通常在qt中打开另一个程序 process模板 QString program “/bin/ls"; QStringList arguments; arguments << "-l" << “-a";QPro…...

什么是机器人学习?
机器人学习是一种涉及人工智能和机器人技术的领域,旨在使机器人能够从经验中学习和改进其性能。通过模仿人类的学习过程,机器人可以通过不断地接收和分析信息来提高自己的技能和表现。机器人学习可以分为监督学习、无监督学习和强化学习等不同类型&#…...

裸机程序--时间片调度
1.为什么自己写一个时间片调度呢 a. 网上其实有很多成熟的时间片调度例程, 包括我最开始参加工作也是抄的网上的例程(还记得当时领导问我看明白了它的调度原理吗, 作为一个自学刚参加工作的我来说, 看懂别人的意思真的很难, 当时只能含糊其词的说看得差不多) b. 在我看来网上的…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
