C#,无监督的K-Medoid聚类算法(K-Medoid Algorithm)与源代码

1 K-Medoid算法
K-Medoid(也称为围绕Medoid的划分)算法是由Kaufman和Rousseeuw于1987年提出的。中间点可以定义为簇中的点,其与簇中所有其他点的相似度最小。
K-medoids聚类是一种无监督的聚类算法,它对未标记数据中的对象进行聚类。
在本文中,我们将了解什么是K-medoids聚类?为什么我们需要它?首先,得出第二个问题的答案:我们需要它,因为K-means聚类有一些缺点,即在这方面,具有极大值的对象可能会严重扭曲对象在簇/组中的分布。因此,它对异常值很敏感。它通过K-medoids聚类(也称为K-means聚类的临时版本)来解决。
在K-medoids聚类中,我们将medoid作为参考点,而不是像K-means聚类那样将簇中对象的质心作为参考点。中间体是群集中位置最集中的对象,或其与所有对象的平均相异性最小。因此,K-medoids算法比K-means算法对噪声更具鲁棒性。

2 K-medoids聚类有三种算法:
PAM(围绕medoid分区)
CLARA(群集大型应用程序)
CLARANS(“随机化”克拉拉)。
在这些PAM中,PAM被认为是最强大的,并被广泛使用。然而,PAM有一个缺点,因为它的时间复杂性(我们将在后面讨论)。因此,在本文中,我们将详细了解PAM算法。
算法
现在我们来看看k-medoids算法内部的情况,如下所示:
步骤1:在给定的数据空间D中初始化k个集群。
步骤2:从数据中的n个对象中随机选择k个对象,并将k个对象分配给k个簇,这样每个对象都被分配给一个且仅一个簇。因此,它成为每个集群的初始中间层。
步骤3:对于所有剩余的非medoid对象,计算所有medoid的成本(通过欧几里德、曼哈顿或切比雪夫方法计算的距离)。
步骤4:现在,将每个剩余的非中间层对象指定给该簇,该簇的中间层到该对象的距离与其他簇的中间层相比是最小的。
步骤5:计算总成本,即,它是所有非medoid对象与其群集medoid之间距离的总和,并将其分配给dj。
第六步:随机选择一个非中间体对象i。
步骤7:现在,暂时将对象i与medoid j交换,然后重复步骤5以重新计算总成本并将其分配给di。
步骤8:如果di<dj,则将步骤7中的临时交换永久化,以形成新的k medoid集。否则撤消步骤7中完成的临时交换。
步骤9:重复步骤4、步骤5、步骤6、步骤7、步骤8。直到没有变化;
3 PAM、CLARA、CLARANS之间的差异
3.1 PAM
与k-means算法相比,它有效地处理了数据中存在的噪声和异常值;因为它使用medoid将对象划分为簇,而不是k-means中的质心。
因为它对整体数据执行聚类,而不是仅对数据集中选定的样本执行聚类。因此,对于大型数据集,它不能有效地工作。
PAM的计算成本很高,因为它在整个数据集上执行集群。
其每次迭代的时间复杂度为O(k*(n-k)^2);其中n是数据中对象的数量,k是簇的数量。
3.2 CLARA
在CLARA中,它首先从数据集中选择数据样本,对这些样本应用PAM,然后从这些样本中输出最佳聚类。
因为它通过从数据中选择样本来应用聚类,所以它处理的是较大的数据集。
随着样本量的增加,其有效性也会增加,反之亦然。
假设它绘制了多个较小的样本,并在其上进行了良好的聚类。如果所选样本有偏差,则不能很好地对总体数据进行聚类。
3.3 CLARANS
在每一步中,它都会选择一个邻居样本进行检查。因此,它不会将搜索限制在特定区域。它给出了基于总体数据的结果。
现在,因为它在每一步都会检查邻居。因此,当集群和对象数量很大时,这很耗时。
在CLARANS中,有一个参数表示局部最优值的数量。就像找到了局部最优值一样,它再次开始随机选取一个节点来找到新的局部最优值。要限制此过程,请在启动时指定上述参数。
因为,它的时间复杂度是O(n^2)。因此,它是其他k-medoids算法中最有效的算法;返回更高质量的群集。
3.4 K-medoids算法的优点
与其他分割算法相比,它有效地处理了数据中存在的噪声和异常值;因为它使用medoid将对象划分为集群。
易于实现且易于理解。
与其他分割算法相比,K-Medoid算法速度相对较快。
它以固定的迭代次数输出最终的对象簇。
3.5 K-medoids算法的缺点
对于同一数据集上的不同运行,可能会产生不同的聚类,因为最初,我们从所有数据对象中随机选择k个medoid,并将它们逐个分配给每个聚类,使其成为该聚类的初始medoid。
它在开始时固定了k(簇/组的数量)的值,因此我们不知道k的值是多少,结果是准确和可区分的。
它的总体计算时间和对象在簇或组中的最终分布取决于初始划分。
因为在这里,我们根据对象与质心的最小距离(而不是k-means中的质心)将对象分布在簇中。因此,在任意形状的聚类中对数据进行聚类是没有用的。
源程序
using System;
using System.IO;
using System.Text;
using System.Linq;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public class K_Medoids{public static List<Crows> Pam(List<Indivaduls> indivadulses, List<Indivaduls> centerPoints){List<Crows> firstCrows = K_medoids(indivadulses, centerPoints);List<Indivaduls> resultCenterPoints = new List<Indivaduls>();for (int i = 0; i < firstCrows.Count; i++){resultCenterPoints.Add(firstCrows[i].CenterPoint);List<Crows> oldOtherCrows = new List<Crows>();oldOtherCrows.AddRange(firstCrows);oldOtherCrows.RemoveAt(i);double oldDiff = AbsoluteDiff(firstCrows[i], oldOtherCrows);int count = firstCrows[i].CrowsPoint.Count;for (int j = 0; j < count; j++){List<Indivaduls> newCenterPoints = new List<Indivaduls>();newCenterPoints.AddRange(centerPoints);newCenterPoints.RemoveAt(i);newCenterPoints.Add(firstCrows[i].CrowsPoint[j]);List<Indivaduls> newOtherCrowsCenterPoints = new List<Indivaduls>();newOtherCrowsCenterPoints.AddRange(centerPoints);newOtherCrowsCenterPoints.RemoveAt(i);List<Crows> newCrows = K_medoids(indivadulses, newCenterPoints);List<Crows> newOtherCrows = new List<Crows>();Crows newCrow = new Crows();foreach (Crows crow in newCrows){if (newOtherCrowsCenterPoints.MyContains(crow.CenterPoint)){newOtherCrows.Add(crow);}else{newCrow = crow;}}double newDiff = AbsoluteDiff(newCrow, newOtherCrows);if (newDiff < oldDiff){resultCenterPoints[i] = newCrow.CenterPoint;oldDiff = newDiff;}}}List<Crows> resultCrows = K_medoids(indivadulses, resultCenterPoints);return resultCrows;}public static List<Crows> K_medoids(List<Indivaduls> indivadulses, List<Indivaduls> centerPoints){List<Crows> resultCrows = new List<Crows>();int indivadulsCount = indivadulses.Count;for (var i = 0; i < centerPoints.Count; i++){resultCrows.Add(new Crows() { CenterPoint = centerPoints[i] });}for (int i = 0; i < indivadulsCount; i++){if (!centerPoints.MyContains(indivadulses[i])){int myNumber = 0;double firstDic = P2PDistance(indivadulses[i], resultCrows[0].CenterPoint);//该点与第一个中心的距离for (int j = 1; j < resultCrows.Count; j++){double otherDic = P2PDistance(indivadulses[i], resultCrows[j].CenterPoint);if (otherDic < firstDic){firstDic = otherDic;myNumber = j;}}resultCrows[myNumber].CrowsPoint.Add(indivadulses[i]);}}return resultCrows;}public static double AbsoluteDiff(Crows centerCrow, List<Crows> otherPoints){int countCrows = otherPoints.Count;double distance = Distance(centerCrow);for (var i = 0; i < countCrows; i++){distance += Distance(otherPoints[i]);}return distance;}public static double Distance(Crows crow){int pointCount = crow.CrowsPoint.Count;double distance = 0.0;for (var i = 0; i < pointCount; i++){distance += P2PDistance(crow.CenterPoint, crow.CrowsPoint[i]);}return distance;}public static double P2PDistance(Indivaduls p1, Indivaduls p2){if (p1.Numbers.Count != p2.Numbers.Count || p1.Numbers.Count == 0){throw new Exception();}int dimension = p1.Numbers.Count;double result = 0.0;for (int i = 0; i < dimension; i++){result += (p1.Numbers[i] - p2.Numbers[i]) * (p1.Numbers[i] - p2.Numbers[i]);}return Math.Sqrt(result);}}public class Indivaduls{public List<double> Numbers { get; set; } = new List<double>();public Indivaduls(){}public bool MyEquals(Indivaduls obj){if (obj.Numbers.Count != Numbers.Count){return false;}for (int i = 0; i < Numbers.Count; i++){if (Numbers[i] != obj.Numbers[i]){return false;}}return true;}}public class Crows{public List<Indivaduls> CrowsPoint { get; set; } = new List<Indivaduls>();public Indivaduls CenterPoint { get; set; } = new Indivaduls();public Crows(){}}public static class ExpandList{public static bool MyContains(this List<Indivaduls> indivadulses, Indivaduls point){foreach (var indivadulse in indivadulses){if (point.MyEquals(indivadulse)){return true;}}return false;}}
}
相关文章:

C#,无监督的K-Medoid聚类算法(K-Medoid Algorithm)与源代码
1 K-Medoid算法 K-Medoid(也称为围绕Medoid的划分)算法是由Kaufman和Rousseeuw于1987年提出的。中间点可以定义为簇中的点,其与簇中所有其他点的相似度最小。 K-medoids聚类是一种无监督的聚类算法,它对未标记数据中的对象进行聚…...

宏定义中#与##的注意事项
1. #是字符串化操作符。它的作用是将宏参数转换成字符串 2. ##是标记粘贴操作符。它的作用是将两个标记连接起来形成一个新的标记 #define TEST1(a) #a #define TEST2(a) b##a/***********************************************************/ 举例:TEST1(hello) 会…...

Java函数式编程
Java函数式编程 Java函数式编程(Functional Programming in Java)是指使用函数式编程范式来编写Java代码的一种编程方式。函数式编程是一种编程范式,它强调使用函数作为基本构建块,并将计算视为数学上的函数求值,避免…...

【深度优先搜索】【树】【C++算法】2003. 每棵子树内缺失的最小基因值
作者推荐 动态规划的时间复杂度优化 本文涉及知识点 深度优先搜索 LeetCode2003. 每棵子树内缺失的最小基因值 有一棵根节点为 0 的 家族树 ,总共包含 n 个节点,节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ,其中…...

电脑开机显示器没有信号而且键盘鼠标不亮怎么解决?
大家在使用电脑的过程,开机没有反应是比较经常遇到的问题,就有用户反映说自己的电脑启动之后,显示器无信号,键盘鼠标灯也不亮,怎么操作都没有效果。对开机有影响的硬件主要是内存条,内存条是非常容易松动的,而且金手指如果氧化了,都会导致开不了机 大家在使用电脑的过程…...

RLWE同态加密编码打包——系数打包
RLWE同态加密的明文域 RLWE的加密方案,如BGV、BFV,加密的对象,实际上是分圆多项式环上的一个整系数多项式。而我们在平时接触到的需要加密的数据,如图像或者工资,通常是一个数。所以,在使用RLWE同态加密时…...

Codeforces Round 930 (Div. 2 ABCDEF题) 视频讲解
A. Shuffle Party Problem Statement You are given an array a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an. Initially, a i i a_ii aii for each 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n. The operation swap ( k ) \texttt{swap}(k) swap(k) for an…...

【LeetCode-中等】209.长度最小的子数组-双指针/滑动窗口
力扣题目链接 1. 暴力解法 这道题的暴力解法是两层嵌套for循环,第一层循环从 i 0 开始遍历至数组末尾,第二层循环从 j i 开始遍历至找到总和大于等于 target 的连续子数组,并将该连续子数组的长度与之前找到的子数组长度相比较࿰…...

MACOS/LINUX/WINDOWS C++ 获取当前可执行程序的完整路径
依赖本人写的多平台编译器宏判断: C/C MACOS、Windows、Linux、HarmonyOS 平台宏判断-CSDN博客 MACOS头文件依赖: #if defined(_MACOS) #include <libproc.h> #endif #include <mach-o/dyld.h> 只需要链接 libSystem.dylib 就行了&#…...
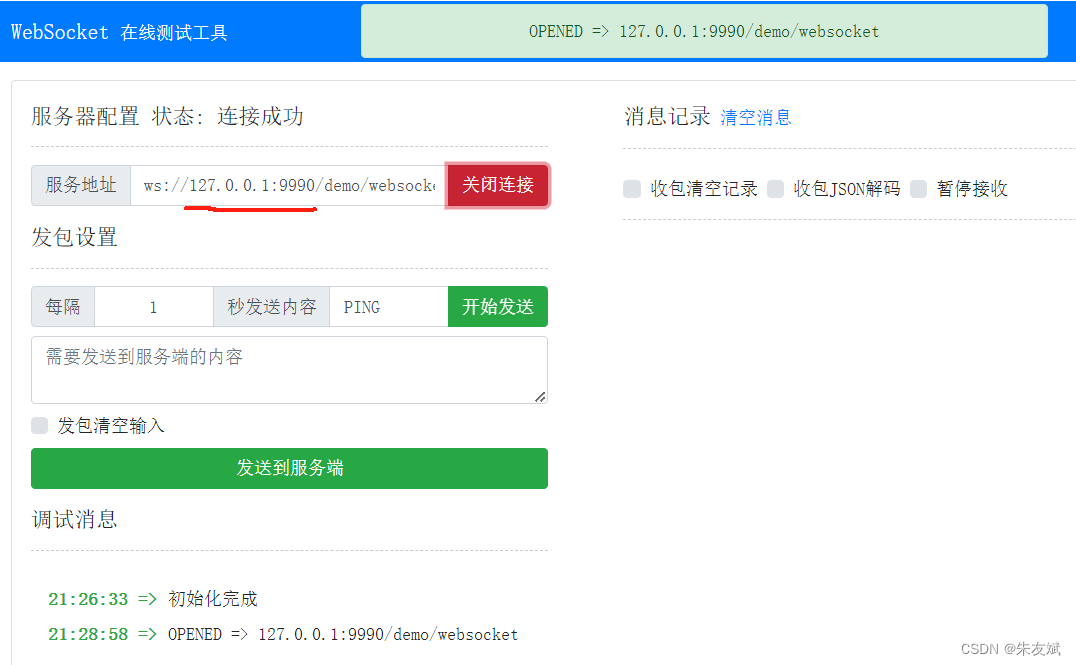
【Nginx笔记02】通过Nginx服务器转发客户端的WebSocket接口到后端服务
这篇文章,主要介绍如何通过Nginx服务器转发客户端的WebSocket接口到后端服务【知识星球】。 目录 一、Nginx配置WebSocket 1.1、Nginx配置内容 1.2、客户端请求地址 1.3、创建WebSocket测试工程 1.4、启动测试 1.5、WebSocket超时问题 1.5.1、设置超时时间 …...
关于高德地图及其APP获取地图数据的研究
刚过完春节没几天,有个客户提出要获取高德地图的数据。 我看了下,回复说:这不是很简单嘛,高德有公开的开放平台,有足够的API支持用户获取数据,开发自己基于高德数据库的应用。 客户回复说:他的要…...

【Python入门教程】Python实现鸡兔同笼
今天跟大家分享一下很久之前自己做的鸡兔同笼求解问题的小游戏,使用公式和基本的判断语句即可实现,可以用来当练手或者消磨时间用。 大家在编代码的时候最重要就是先理清逻辑思路,例如应该套几层循环、分几个模块等等。然后在编码时可以先随意…...
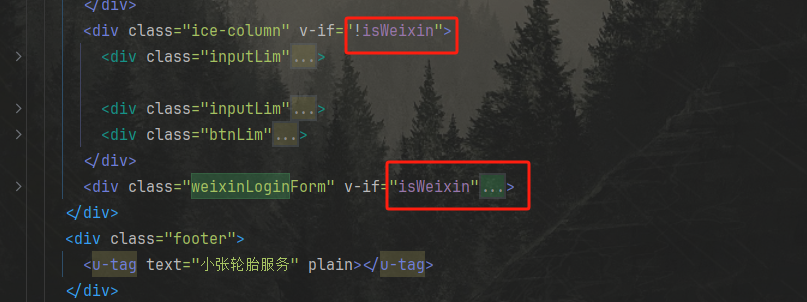
微信小程序,h5端自适应登陆方式
微信小程序端只显示登陆(获取opid),h5端显示通过账户密码登陆 例如: 通过下面的变量控制: const isWeixin ref(false); // #ifdef MP-WEIXIN isWeixin.value true; // #endif...
)
物体检测-系列教程20:YOLOV5 源码解析10 (Model类前向传播、forward_once函数、_initialize_biases函数)
😎😎😎物体检测-系列教程 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 点我下载源码 14、Model类 14.2 前向传播 def forward(self, x, augmentFalse, profileFalse):if augm…...
贪吃蛇(C语言)步骤讲解
一:文章大概 使用C语言在windows环境的控制台中模拟实现经典小游戏 实现基本功能: 1.贪吃蛇地图绘制 2.蛇吃食物的功能(上,下,左,右方向控制蛇的动作) 3.蛇撞墙死亡 4.计算得分 5.蛇身加…...

MySQL 数据库表设计和优化
一、数据结构设计 正确的数据结构设计对数据库的性能是非常重要的。 在设计数据表时,尽量遵循一下几点: 将数据分解为合适的表,每个表都应该有清晰定义的目的,避免将过多的数据存储在单个表中。使用适当的数据类型来存储数据&…...

JavaScript进阶-高阶技巧
文章目录 高阶技巧深浅拷贝浅拷贝深拷贝 异常处理throw抛异常try/caych捕获异常debugger 处理thisthis指向改变this 性能优化防抖节流 高阶技巧 深浅拷贝 只针对引用类型 浅拷贝 拷贝对象后,里面的属性值是简单数据类型直接拷贝值,如果属性值是引用数…...

C语言中“#“和“##“的用法
1. 前言 # :把宏参数变为一个字符串, ##:把两个宏参数贴合在一起. 2. 一般用法 #include<stdio.h> #define toString(str) #str //转字符串 #define conStr(a,b) (a##b)//连接 int main() { printf(toString(12345)): //输出字符串&q…...
)
Linux命令-clock命令(用于调整 RTC 时间)
说明 clock命令用于调整 RTC 时间。 RTC 是电脑内建的硬件时间,执行这项指令可以显示现在时刻,调整硬件时钟的时间,将系统时间设成与硬件时钟之时间一致,或是把系统时间回存到硬件时钟。 语法 clock [--adjust][--debug][--dir…...

编程笔记 Golang基础 045 math包
编程笔记 Golang基础 045 math包 一、math包主要功能常量:函数:数值运算:三角函数:对数函数:随机数相关: 二、示例代码一三、示例代码二小结 Go 语言的标准库 math 提供了一系列基础数学函数和常量…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...
