信号系统之复数傅立叶变换
1 实数DFT
傅里叶变换系列的所有四个成员(DFT、DTFT、傅里叶变换和傅里叶级数)都可以用实数或复数进行。由于DSP主要关心的是DFT,所以就以它为例。
可以根据以下方程定义离散傅里叶变换的实数版本:
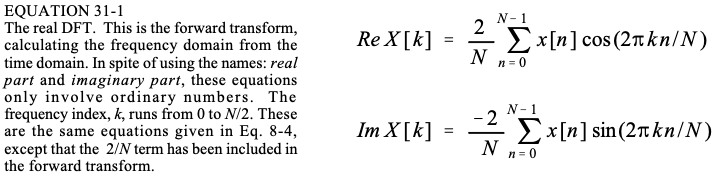
一个 N 个样本时域信号 被分解为一组N/2+1的cosine信号和N/2+1的sine信号。
对于复数DFT,当正弦曲线用复数表示时,允许加法和减法,但禁止乘法和除法。
实数DFT无法处理频谱的负频率部分,这通常是在混叠、循环卷积和幅度调制中发生的情况。还有对ReX [0] 和ReX [N/2]的特殊处理,因为需要除以2,这在程序方便实现,但在方程中不便处理。
2 数学等价
第一步是展示如何将正弦波和余弦波写成复数方程:

可以将这种关系重新排列成另外两种形式:
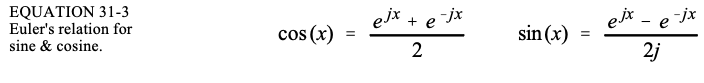
对上式做一些改变:

每个表达式都是两个指数之和:一个包含正频率 ( ω \omega ω),另一个包含负频率 ( − ω -\omega −ω)。换句话说,当正弦波和余弦波写成复数时,自动包含频谱的负部分。正负频率同等对待;它需要每个波形的二分之一才能形成完整的波形。
3 复数DFT
正向复数 DFT 以极坐标形式表示,由下式给出:

或者,可以使用欧拉关系将正向变换重写为矩形形式:
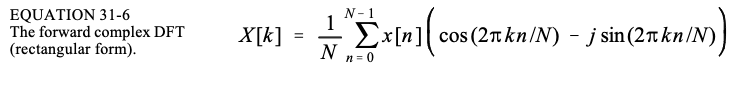
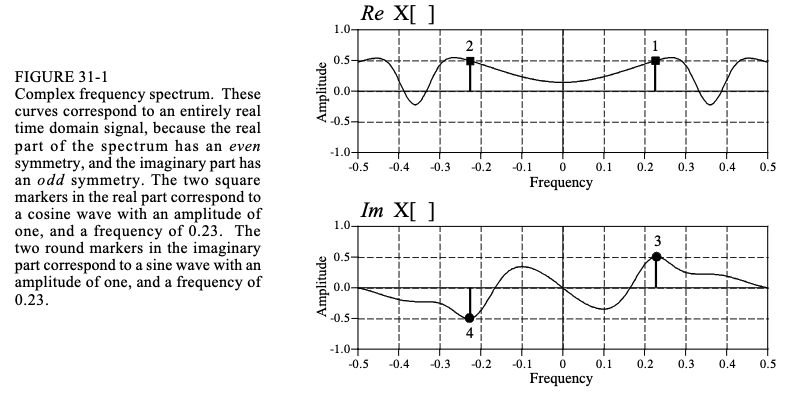
图 31-1 说明了复数 DFT 的频谱。该图假设时域是完全实数的,即其虚部为零。显示复杂频谱有两种常见方法,如图所示,零频率可以放置在中心,正频率放置在右侧,负频率放置在左侧。这是考虑完整频谱的最佳方式,也是显示非周期频谱的唯一方式。
问题在于离散信号的频谱是周期性的(例如 DFT 和 DTFT)。这意味着 -0.5 到 0.5 之间的所有值都会向左和向右重复无限次。在这种情况下,0 到 1.0 之间的频谱包含与 0.5 到 0.5 之间的频谱相同的信息。当制作图表时,如图31-1,通常使用-0.5到0.5的约定。然而,许多方程和程序使用 0 到 1.0 的形式。例如,在等式31-5 和 31-6 中频率索引 k 从 0 到 N-1(与 0 到 1.0 一致)。但如果需要,可以将其编写为从 -N/2 到 N/2-1(与 -0.5 到 0.5 一致)运行。
使用图 31-1 中的频谱作为指导,可以检查逆复数 DFT 如何重建时域信号。逆复数 DFT 以极坐标形式表示,由下式给出:

使用欧拉关系,可以将其写成矩形形式:

31-7 是逆 DFT 的通常写法,但式 31-9可以更容易理解。换句话说,频域实部的每个值都会向时域贡献一个实余弦波和一个虚正弦波。同样,频域虚部中的每个值都贡献一个实正弦波和一个虚余弦波。时域是通过将所有这些实部和虚部正弦曲线相加得出的。重要的概念是频域中的每个值都会在时域中产生实数正弦曲线和虚数正弦曲线。
例如,假设想要重建频率为 2 π k / N 2\pi k/N 2πk/N的单位振幅余弦波。这需要正频率和负频率,均来自频谱的实部。图 31-1 中的两个方形标记就是一个例子,频率设置为:k/N=0.23。对于正频率0.23(图 31-1 中标记为 2)在时域中的贡献为:
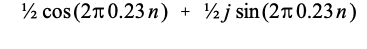
同样,负频率-0.23 处的(图 31-1 中标记为 2)也会向时域贡献一个余弦波和一个虚正弦波:
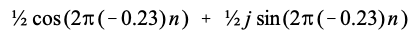
根据:
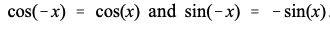
上式可以化为:

将正频率和负频率的贡献相加即可重建时域信号:
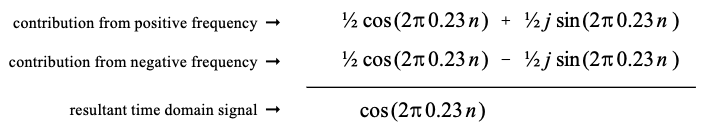
以同样的方式,可以在时域合成正弦波。在这种情况下,需要频谱虚部的正频率和负频率。图 31-1 中的圆形标记显示了这一点。根据方程31-8,这些频谱值向时域贡献正弦波和虚余弦波。虚余弦波相消,而实正弦波相加:
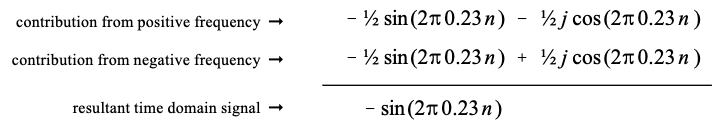
注意,即使正频率具有正值,也会生成负正弦波。这种符号反转是复数 DFT 数学的固有部分。这种相同的符号反转通常用于真实的 DFT。也就是说,频谱的虚部中的正值对应于负正弦波。大多数作者将这种符号反转包含在实傅里叶变换的定义中,以使其与其复数对应物保持一致。关键是,这种符号反转必须在复数傅里叶变换中使用,但在实数傅里叶变换中只是一个选项。
复数傅立叶变换的对称性非常重要。如图31-1所示,实时域信号对应于具有偶数实部和奇数虚部的频谱。换句话说,负频率和正频率在实部(如图31-1中的点1和2)具有相同的符号,但在虚部(点3和4)具有相反的符号。
这就引出了另一个话题:时域的虚部。到目前为止,都假设时域是完全实数的,即虚部为零。然而,复杂的傅里叶变换不需要这个。
虚数时域信号的物理意义是什么?通常情况下没有。这只是复杂数学允许的事情,与生活的世界没有对应关系。但是,在某些应用程序中可以出于数学目的使用或操纵它。
4 傅里叶变换家族
1)四个傅立叶变换
时域信号可以是连续的或离散的,也可以是周期性的或非周期性的。这定义了四种类型的傅里叶变换:
- 离散傅里叶变换(离散、周期)
- 离散时间傅里叶变换(离散、非周期)
- 傅里叶级数(连续、周期)
- 傅里叶变换(连续、非周期)
不要试图理解这些名称背后的原因,根本不存在。
如果信号在一个域中是离散的,则在另一域中它将是周期性的。同样,如果信号在一个域中是连续的,则在另一域中将是非周期性的。
连续信号用括号 ( ) 表示,离散信号用括号 [ ] 表示。没有符号来指示信号是周期性的还是非周期性的。
2)实数与复数
这四种变换中的每一种都有一个复数版本和一个实数版本:
- 复数版本具有复数时域信号和复数频域信号。
- 实数版本具有一个实时域信号和两个实频域信号。
在复数情况下使用正频率和负频率,而在实数变换中仅使用正频率。复数的变换通常写成指数形式,但如果需要,可以使用欧拉关系将它们更改为余弦和正弦形式。
3)分析与合成
每个变换都有一个分析方程(也称为正变换)和一个合成方程(也称为逆变换):
- 分析方程描述了如何根据时域中的所有值计算频域中的每个值。
- 合成方程描述了如何基于频域中的所有值来计算时域中的每个值。
4)时域表示法
连续时域信号称为x(t),离散时域信号称为x[n] :
- 对于复数的变换,这些信号是复数的。
- 对于实数变换,这些信号是实数。
所有时域信号从负无穷延伸到正无穷。然而,如果时域是周期性的,我们只关心单个周期,因为其余的都是多余的。变量 T 和 N 分别表示时域中连续和离散信号的周期。
5)频域表示法
复数连续频率信号为 X ( ω ) X(\omega) X(ω),如果是实数则为 R e X ( ω ) ReX(\omega) ReX(ω)和 I m X ( ω ) ImX(\omega) ImX(ω)。
复数离散频率信号为 X [ k ] X[k] X[k],如果是实数则为 R e X [ k ] ReX[k] ReX[k]和 I m X [ k ] ImX[k] ImX[k]。
复数变换具有从负无穷大到零的负频率和从零到正无穷大的正频率。实数变换仅使用正频率。如果频域是周期性的,只关心单个周期,因为其余的都是多余的。对于连续频域,自变量 ω \omega ω 构成从 − π -\pi −π到 π \pi π的一个完整周期。在离散情况下,k 构成从 0 到 N-1 的周期。
6)分析方程
分析方程通过相关进行运算,即将时域信号乘以正弦曲线并在适当的时域部分上积分(连续时域)或求和(离散时域):
- 如果时域信号是非周期性的,则适当的部分是从负无穷大到正无穷大。
- 如果时域信号是周期性的,则适当的部分位于任何一个完整周期上。
此处显示的方程是通过以下时间段内的积分(或求和)编写的:0 到 T(或 0 到 N-1)。然而,任何其他完整的周期都会给出相同的结果,即 -T 到 0、-T/2 到 T/2 等。
7)合成方程
合成方程描述了如何根据频域中的所有点计算时域中的单个值。这是通过将频域乘以正弦曲线,并在适当的频域部分上积分(连续频域)或求和(离散频域)来完成的:
- 如果频域是复数且非周期性的,则适当的部分是负无穷到正无穷。
- 如果频域是复数且周期性的,适当的部分是一个完整的周期,即 − π -\pi −π到 π \pi π(连续频域),或0到N-1(离散频域)。
- 如果频域是实数且非周期性的,则适当的部分是零到正无穷大,即只有正频率。
- 最后,如果频域是实数且周期性的,则适当的部分是包含正频率的半个周期,即 0 到 π \pi π(连续频域)或 0 到 N/2(离散频域)。
8)比例因子
为了使分析和合成方程相互抵消,必须在一个或另一个方程上放置比例因子。在表 31-1 中,将比例因子与分析方程放在一起:
- 在复数情况下,这些缩放因子为:1/N、1/T 或 1/2 π \pi π。
- 由于实数变换不使用负频率,因此缩放因子是原来的两倍:2/N、2/T 或 1/ π \pi π。实数变换还在频谱虚部的计算中包含负号(用于使实数变换与复数变换更加一致的选项)。
- 最后,实 DFT 和实傅里叶级数的综合方程具有涉及 ReX (0) 和 ReX[N/2] 的特殊缩放指令。
9)Variations

5 为什么使用复数傅里叶变换




相关文章:

信号系统之复数傅立叶变换
1 实数DFT 傅里叶变换系列的所有四个成员(DFT、DTFT、傅里叶变换和傅里叶级数)都可以用实数或复数进行。由于DSP主要关心的是DFT,所以就以它为例。 可以根据以下方程定义离散傅里叶变换的实数版本: 一个 N 个样本时域信号 被分解…...

Unity - 相机画面为黑白效果
一、 在Hierarchy中创建一个Global Volume,并设置它为局部作用 二、 将场景出现的作用域范围缩小至相机所在位置,将相机包含即可。 三、添加覆盖组件Color Adjustments,并将Saturation直接拉为-100 。 此时,相机拍摄画面为黑白,场景视图中…...

哈啰Java 春招 24届
时长 1h 3. 为什么使用分布式ID,解决了什么问题 4. Leaf算法了解吗?讲一下原理和工作流程以及优缺点 5. 有没有可能导致id重复?该如何解决? 6. 项目中redis是如何运用的? 7. 项目中分布式锁是如何实现的? 8…...
)
《剑指 Offer》专项突破版 - 面试题 68 : 查找插入位置/ 69 : 山峰数组的顶部(C++ 实现)
目录 面试题 68 : 查找插入位置 面试题 69 : 山峰数组的顶部 面试题 68 : 查找插入位置 题目: 输入一个排序的整数数组 nums 和一个目标指 t,如果数组 nums 中包含 t,则返回 t 在数组中的下标;如果数组 nums 中不包含 t&#…...
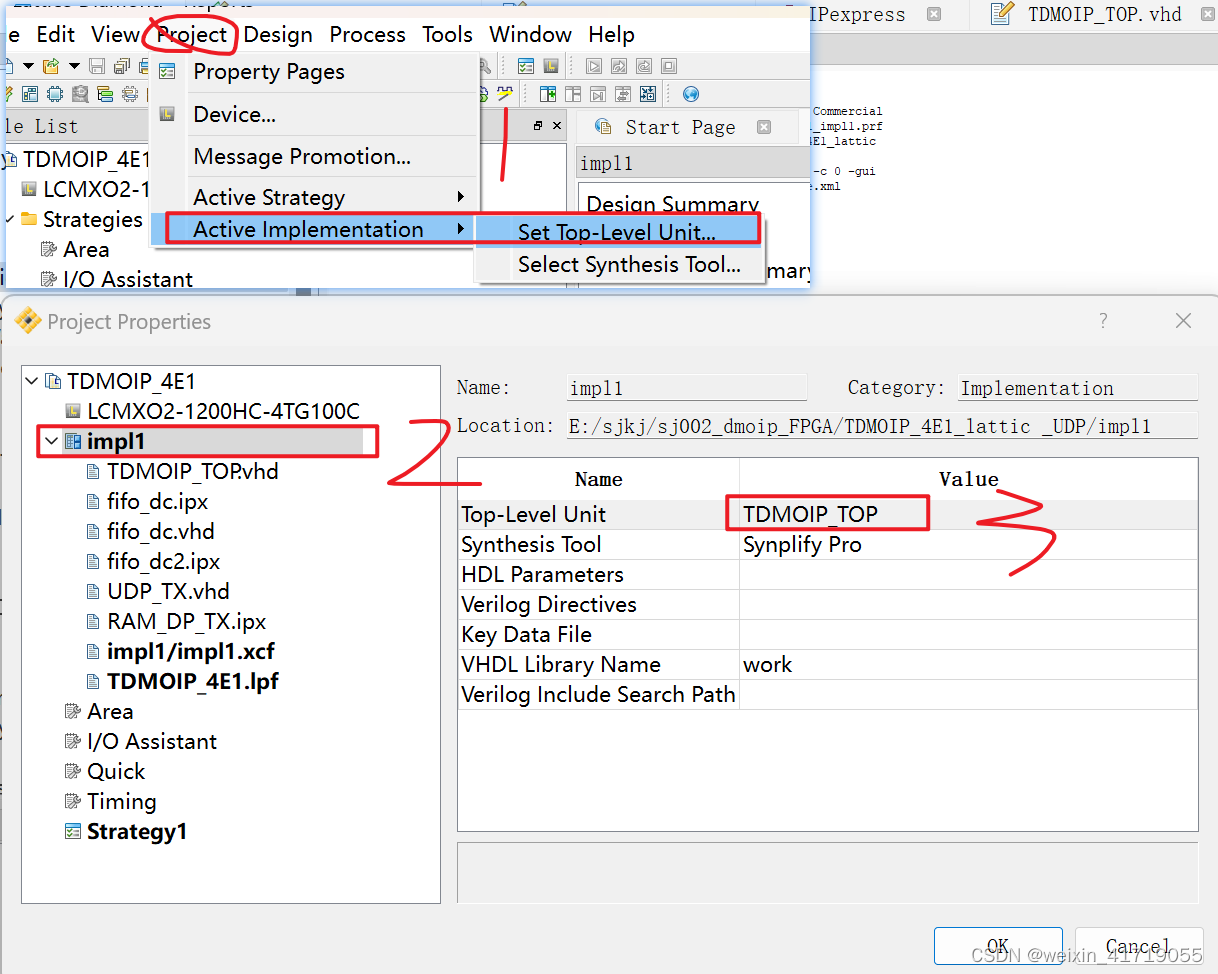
赖迪思软件 lattice Diamond
问题1:工程编译好后,git上传,变更分支又切换回来,再次编译有时候失败,所以配置好的管脚变成默认的,生成的IP核变成名变粗(顶部文件,管脚配置显示IP核输入输出信号配置)。…...
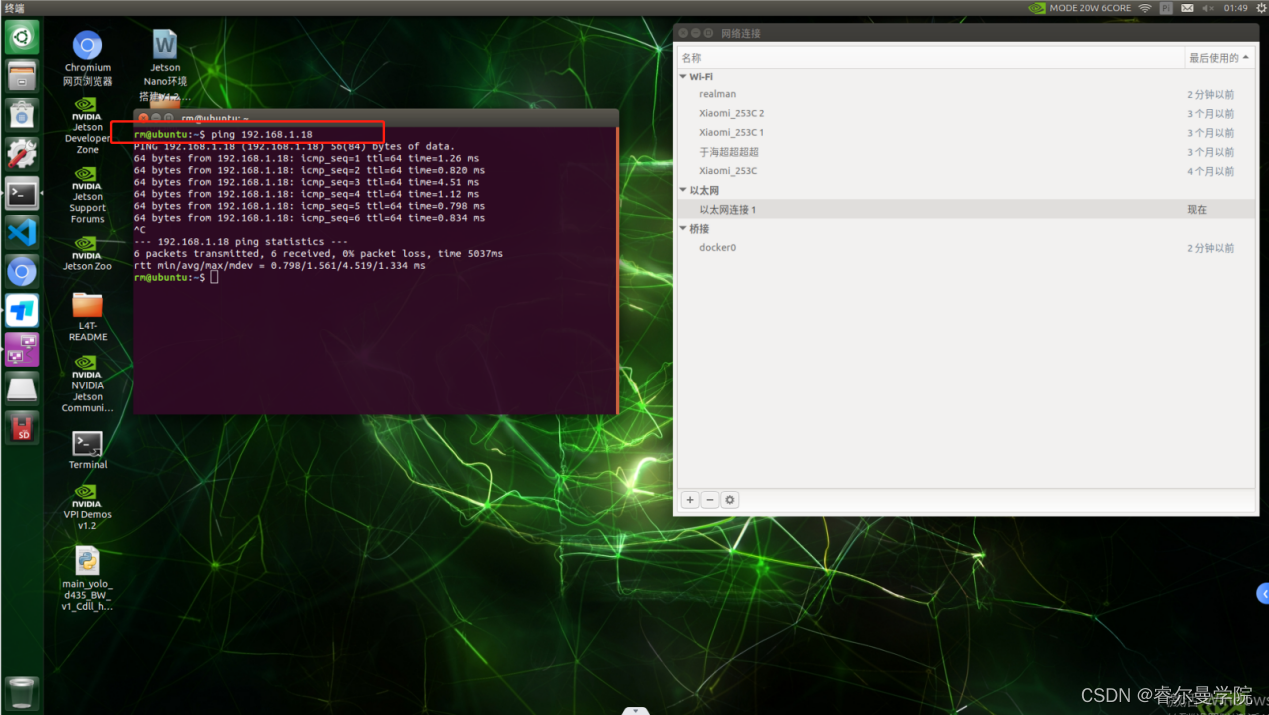
ROS开发基础-Linux基础第四部(开发板设置本地IP)
一 、网线连接设备 使用网线连接jetson NX与机械臂,如下图所示: 二、 修改上位机IPV4 IP ①测试是否可连接。网线连接机械臂之后,在桌面打开终端输入命令“ping 192.168.1.18”,如不可正常通信,可按照下述步骤进行设置。 ②在U…...
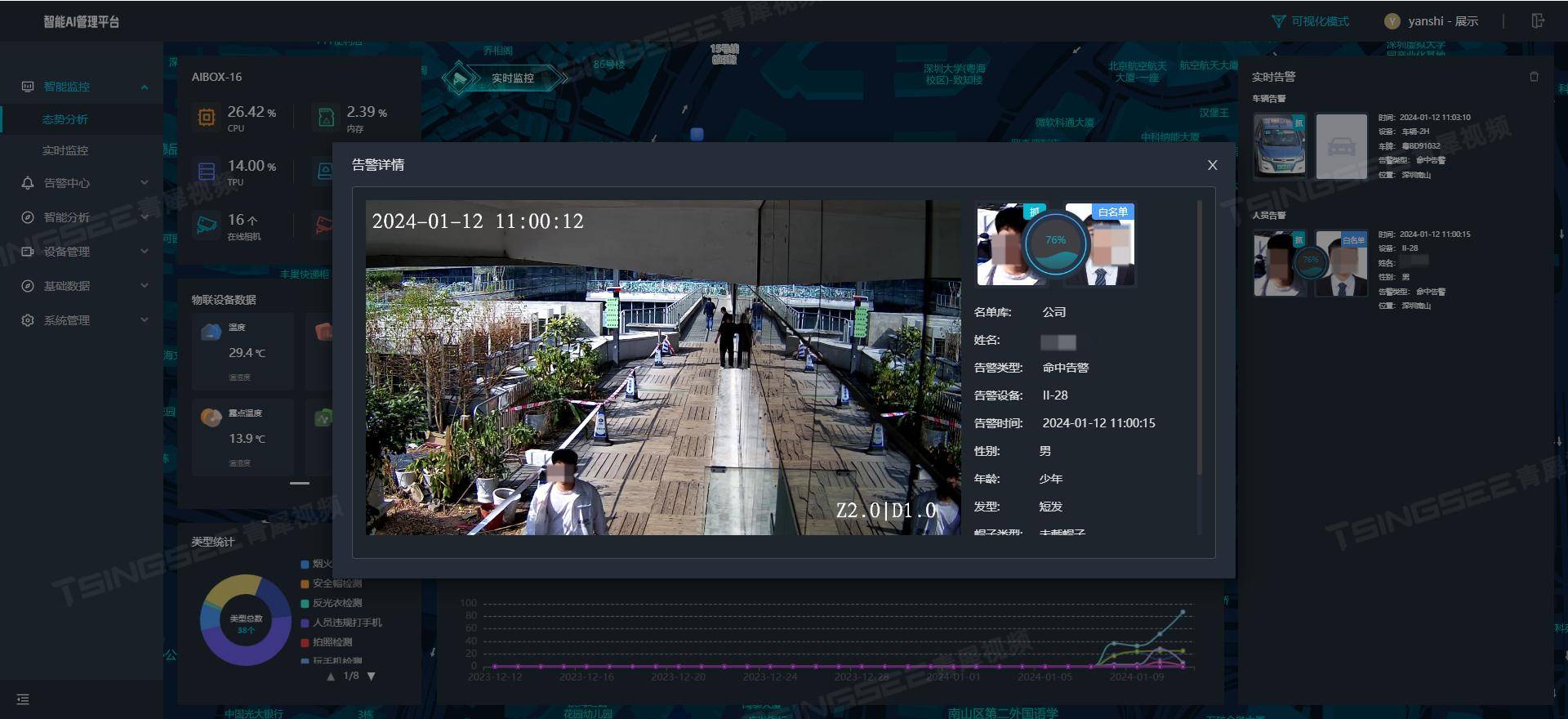
TSINGSEE青犀AI智能分析网关V4智慧油田安全生产监管方案
一、方案背景 随着科技的不断发展,视频监控技术在油田行业中得到了广泛应用。为了提高油田生产的安全性和效率,建设一套智能视频监控平台保障安全生产显得尤为重要。本方案采用先进的视频分析技术、物联网技术、云计算技术、大数据和人工智能技术&#…...

C++基于多设计模式下的同步异步日志系统day3
C基于多设计模式下的同步&异步日志系统day3 📟作者主页:慢热的陕西人 🌴专栏链接:C基于多设计模式下的同步&异步日志系统 📣欢迎各位大佬👍点赞🔥关注🚓收藏,&am…...

Cypher语句查询neo4j数据库教程
文章目录 Cypher介绍执行Cypher语句查询总结 Cypher介绍 NodeMatcher和RelationshipMatcher能够表达的匹配条件相对简单,更加复杂的查询还是需要用Cypher语句来表达。 Py2neo本身支持执行Cypher语句的执行,可以将复杂的查询写成Cypher语句,…...
【ESP32 IDF快速入门】点亮第一个LED灯与流水灯
文章目录 前言一、有哪些工作模式?1.1 GPIO的详细介绍1.2 GPIO的内部框图输入模式输出部分 二、GPIO操作函数2.1 GPIO 汇总2.2 GPIO操作函数gpio_config配置引脚reset 引脚函数设置引脚电平选中对应引脚设置引脚的方向 2.3 点亮第一个灯 三、流水灯总结 前言 ESP32…...
再见,Visual Basic——曾经风靡一时的编程语言
2020年3月,微软团队宣布了对Visual Basic(VB)的“终审判决”:不再进行开发或增加新功能。这意味着曾经风光无限的VB正式退出了历史舞台。 VB是微软推出的首款可视化编程软件,自1991年问世以来,便受到了广大…...
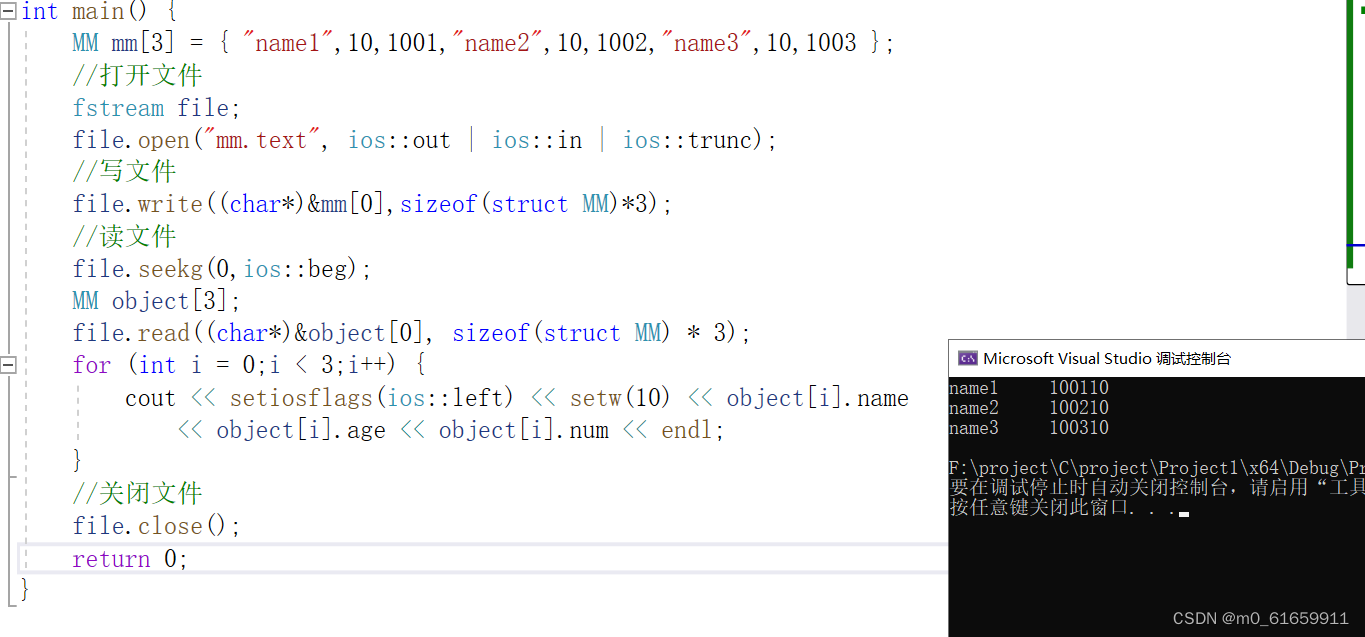
【C++精简版回顾】18.文件操作
1.文件操作头文件 2.操作文件所用到的函数 1.文件io 1.头文件 #include<fstream> 2.打开文件 (1)函数名 文件对象.open (2)函数参数 /* ios::out 可读 ios::in 可…...
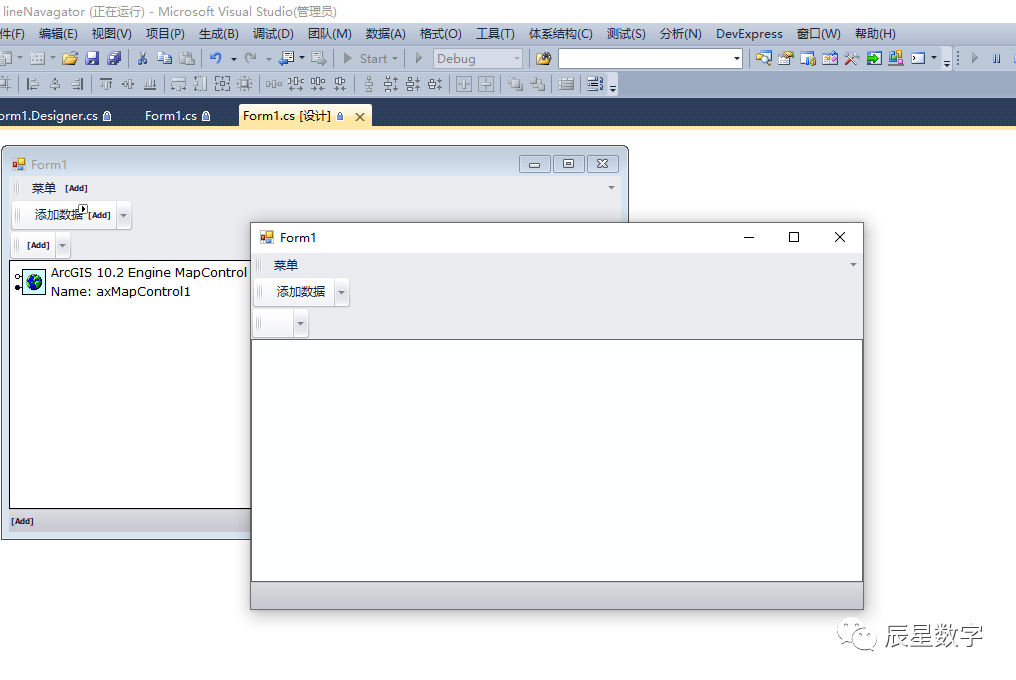
【解决方案】ArcGIS Engine二次开发时,运行后出现“正尝试在 OS 加载程序锁内执行托管代码。不要尝试在 DllMain...”
我们在做ArcGIS Engine二次开发时,特别是新手,安装好了开发环境,满怀信心的准备将按照教程搭建好的框架在Visual Studio中进行运行。点击运行后,却出现了“正尝试在 OS 加载程序锁内执行托管代码。不要尝试在 DllMain 或映像初始化…...
新项目,Linux上一键安装MySQL,Redis,Nacos,Minio
大家好,我是 jonssonyan 分享一个我的一个开源项目,这是一个在 Linux 平台上一键安装各种软件的脚本项目,脚本使用 Shell 语言编写,后续还会增加更多软件的一键安装,代码在 GitHub 上全部开源的,开源地址如…...

Rust 从 PyTorch 到 Burn
一、性能轮盘赌 机器码相同,但放置在不同的地址上,性能可能截然不同。 作为软件开发人员,我们经常假设特定代码的性能仅由代码本身和运行它的硬件决定。这种假设让我们在优化代码以获得更好性能时感到有控制力。虽然在大多数情况下这种假设…...

Swin-Transformer网络代码实现
还是参考导师级别博主霹雳吧啦Wz的个人空间-霹雳吧啦Wz个人主页-哔哩哔哩视频 博主写的博客Swin-Transformer网络结构详解_swin transformer-CSDN博客 视频理论讲解12.1 Swin-Transformer网络结构详解_哔哩哔哩_bilibili pytorch实现12.2 使用Pytorch搭建Swin-Transformer网…...
Java ZooKeeper-RocketMQ 面试题
Java ZooKeeper-RocketMQ 面试题 前言1、谈谈你对ZooKeeper的理解 ?2、Zookeeper的工作原理(Zab协议)3、谈谈你对分布式锁的理解,以及分布式锁的实现?4、 zookeeper 是如何保证事务的顺序一致性的?5、 zook…...

css制作瀑布流布局
CSS制作瀑布流布局的步骤如下: HTML结构:使用无序列表ul和列表项li来创建网格布局。 <ul class"grid"><li><img src"image1.jpg"></li><li><img src"image2.jpg"></li><li…...

Redis 的哨兵模式配置
1.配置 vim sentinel.conf# mymaster 给主机起的名字 # 192.168.205.128 主机的ip地址 # 6379 端口号 # 2 当几个哨兵发现主观宕机,则判定为客观宕机。 原则上是大于一半。比如三个哨兵,则设置为 2 sentinel monitor mymaster 192.168.205.128 63…...

基于单片机的继电器参数测试系统设计
摘要:由于原有测试系统在参数设置上过于单一,在对继电器测试过程中需要多次进行器件连接,导致对其测试准确度下降,会造成继电器的二次损伤,基于单片机研究继电器参数测试系统的设计方法。在硬件设计上,构建二级模式集散控制框架,利用单片机进行数据采集和处理,满足实时…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
