Leetcoder Day27| 贪心算法part01
语言:Java/Go
理论
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
什么时候用贪心?可以用局部最优退出全局最优,并且想不到反例到情况
贪心的一般解题步骤
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
455.分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
- 输入: g = [1,2,3], s = [1,1]
- 输出: 1 解释:你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1,2,3。虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。所以你应该输出 1。
示例 2:
- 输入: g = [1,2], s = [1,2,3]
- 输出: 2
- 解释:你有两个孩子和三块小饼干,2 个孩子的胃口值分别是 1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2.
本题的目标是满足更多孩子的胃口,因此大的饼干就优先满足胃口大的孩子,才会确保没有资源浪费。因此局部最优解就是将一定尺寸的饼干尽量喂给与这个尺寸接近胃口的孩子。全局最优就是喂饱尽可能多的孩子。可以先将饼干和胃口数组进行排序,从后向前遍历孩子数组,将大饼干给胃口大的孩子,并且设置一个count统计满足小孩的数量。
class Solution {public int findContentChildren(int[] g, int[] s) {//先对两个数组进行排序Arrays.sort(g);Arrays.sort(s);int count=0;int index=s.length-1; //饼干数组的下标for(int i=g.length-1;i>=0;i--){//先遍历胃口if(index>=0 && g[i]<=s[index]){ //再去查找饼干count++;index--; //满足条件才会把饼干分配出去,饼干的指针也往前移动}}return count;}
}⚠️注意:如果是从后向前遍历,应该先遍历胃口再遍历饼干,因为这样才不会出现饼干没有合理分配的情况。如果是用小饼干喂饱小胃口,则需要先遍历饼干,再遍历胃口。
376. 摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
- 输入: [1,7,4,9,2,5]
- 输出: 6
- 解释: 整个序列均为摆动序列。
示例 2:
- 输入: [1,17,5,10,13,15,10,5,16,8]
- 输出: 7
- 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
本题目的是通过删除某些元素,找到最长的摆动子序列并返回其长度。摆动序列如果在一个坐标轴上描点,应该是持续存在n个峰值的序列。如下图:

可以看出需要删除的节点应该是,单调递增/递减时,非端点的节点。此时一个坡度上会有两个局部峰值。全局最优就是找到局部峰值最多的序列。因为本题返回最长子序列的长度,所以不需要进行删除操作,只需要统计局部峰值的个数即可。
计算当前节点和前后节点的关系:prediff(nums[i] - nums[i-1])和curdiff(nums[i+1] - nums[i])
若prediff < 0 && curdiff > 0或者prediff > 0 && curdiff < 0,满足这两个条件的时候,说明nums[i-1],nums[i],nums[i+1]均为峰值。- 若遇到平坡,假设上坡后平坡:即prediff > 0 && curdiff = 0,遇到最后一个平坡节点时候,应该是这样的条件:prediff = 0 && curdiff < 0,将这个节点保留,其他平坡的节点都删除。所以当前峰值的条件为(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)第一个情况就是下坡,第二个情况为上坡。
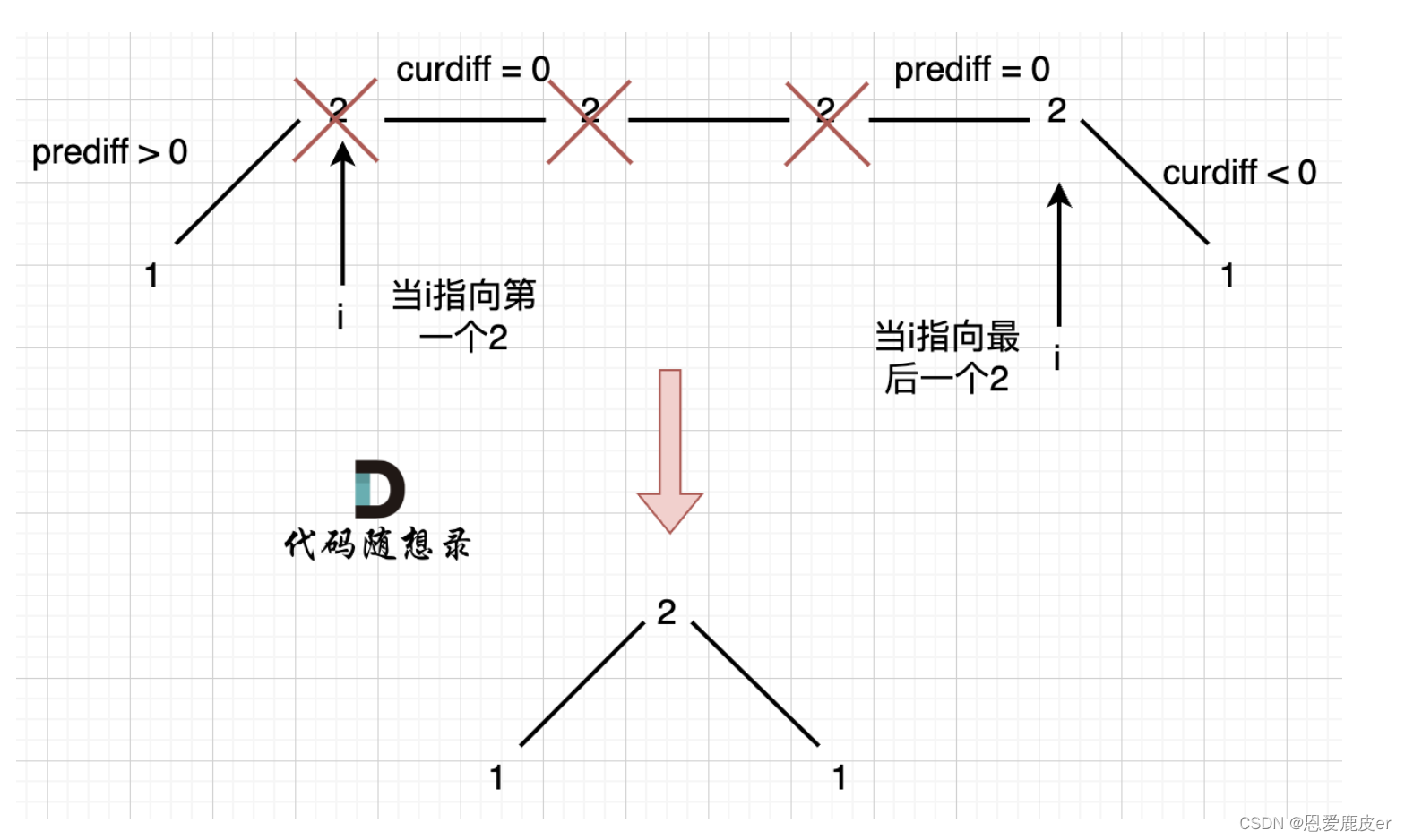
- 若遇到单调坡度有平坡,我们只需要在 这个坡度 摆动变化的时候,更新 prediff 就行,这样 prediff 在 单调区间有平坡的时候 就不会发生变化,造成误判。
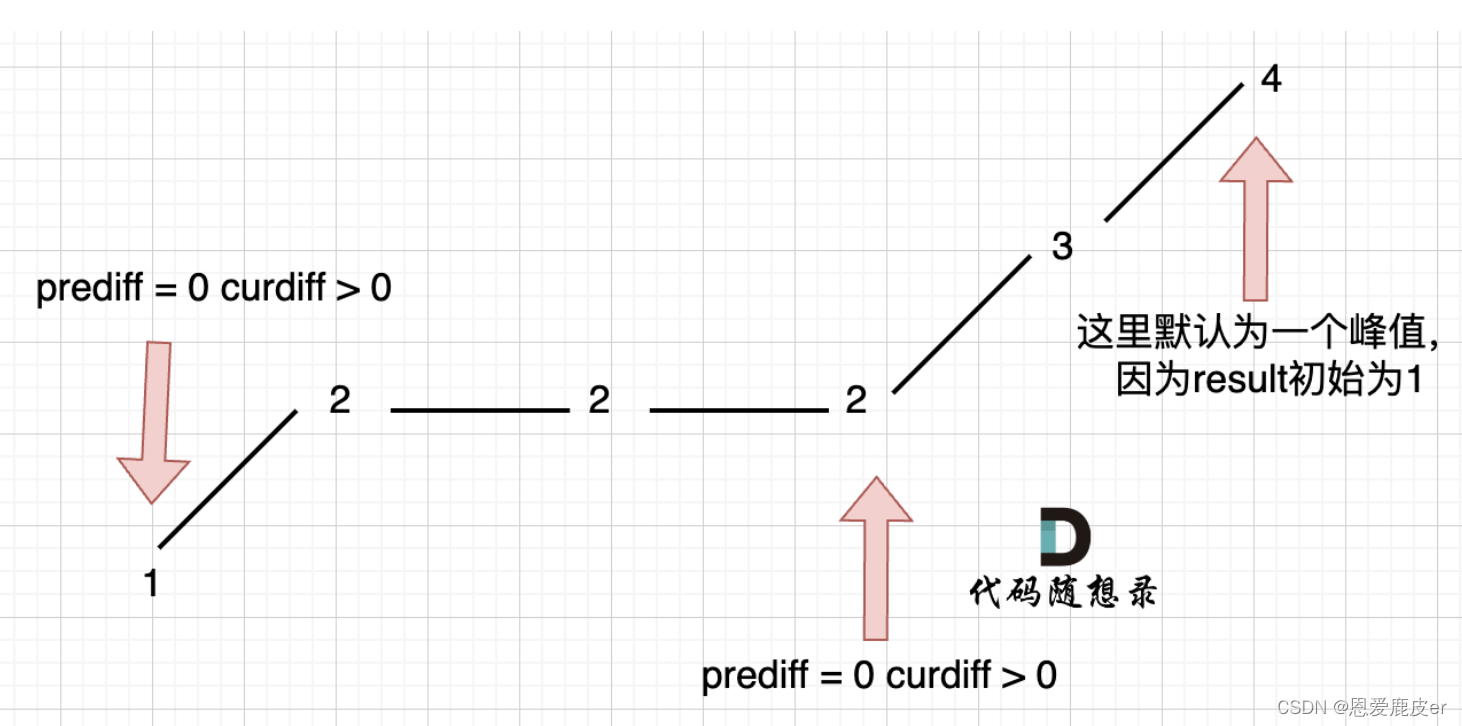
数组首尾两端:题目中说了,如果只有两个不同的元素,那摆动序列也是 2。例如序列[2,5],如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。因为我们在计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i])的时候,至少需要三个数字才能计算,而数组只有两个数字。这里我们可以写死,就是 如果只有两个元素,且元素不同,那么结果为 2。也可以不写死,假设数组最前面还有一个数字,那这个数字应该是什么呢?之前我们在 讨论 情况一:相同数字连续 的时候, prediff = 0 ,curdiff < 0 或者 >0 也记为波谷。那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0
class Solution {public int wiggleMaxLength(int[] nums) {if(nums.length<=1) return nums.length;int curDiff=0; //记录当前节点和后一个节点的差值int preDiff=0; //记录前一个节点和当前节点的差值int result=1;for(int i=0;i<nums.length-1;i++){curDiff=nums[i+1]-nums[i];if(preDiff<=0&&curDiff>0 || preDiff>=0 && curDiff<0){//出现峰谷的时候result++;preDiff=curDiff;}}return result;}
}53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
- 输入: [-2,1,-3,4,-1,2,1,-5,4]
- 输出: 6
- 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
本题跟上题的区别在于,要求连续。因此不可以进行删除也不可以对数组重排序。本题的直接思路就是两层for循环嵌套,但是时间复杂度太高。可以考虑用贪心算法或动态规划算法。
先尝试找局部最优:比如看前两个元素:-2,1,肯定会先以1作为开头,把1加入到结果中,在sum上加上1,任何负值只会减少和的值。当以1为开头时,又遇到了-3,这时sum变成了负值,所以将1从结果中删除,从3点后面一个元素开始判断,以此类推。还要设置变量maxSum记录最大的和。因此,如果当加上nums[i]时sum变为负数时,就将sum变为0重新计算。
class Solution {public int maxSubArray(int[] nums) {if(nums.length==1) return nums[0];int sum=0;int maxSum=Integer.MIN_VALUE;for(int i=0;i<nums.length;i++){sum+=nums[i];maxSum=Math.max(sum, maxSum);if(sum<=0) sum=0;}return maxSum;}
}相关文章:

Leetcoder Day27| 贪心算法part01
语言:Java/Go 理论 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 什么时候用贪心?可以用局部最优退出全局最优,并且想不到反例到情况 贪心的一般解题步骤 将问题分解为若干个子问题找出适合的贪心策略求解每一个子…...

SpringBoot自动配置中bean的加载控制
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...

Linux系统运维脚本:根据菜单选择要登录到的Linux主机,方便维护多个linux服务器
目 录 一、要求 二、解决方案 (一)解决思路 (二)方案 三、脚本程序实现 (一)脚本代码和解释 1、定义hosts.txt文件 2、脚本代码 3、代码解释 (二)脚本验证 1…...

蓝桥杯练习题——二分
1.借教室 思路 1.随着订单的增加,每天可用的教室越来越少,二分查找最后一个教室没有出现负数的订单编号 2.每个订单的操作是 [s, t] 全部减去 d #include<iostream> #include<cstring> using namespace std; const int N 1e6 10; int d[…...
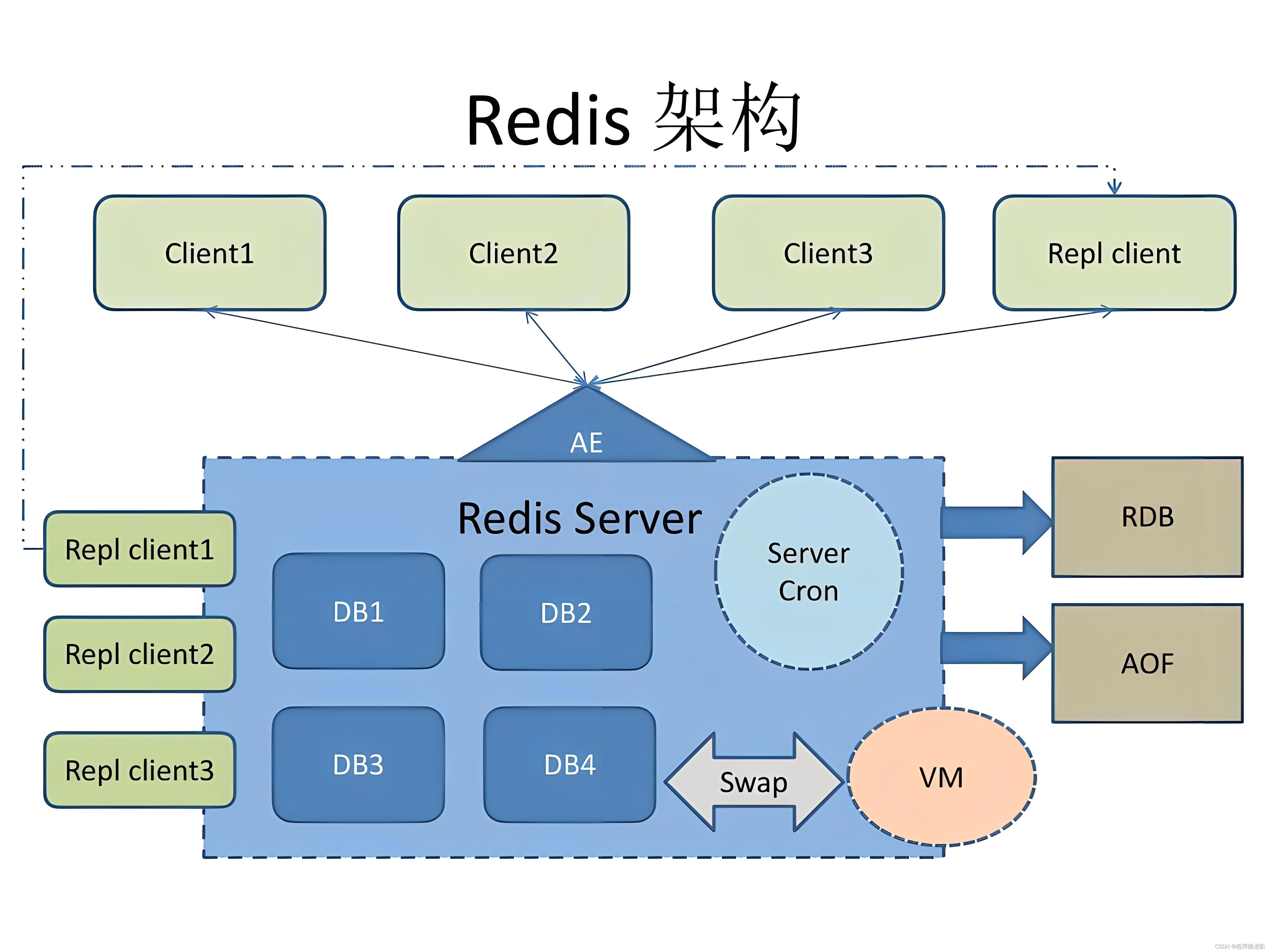
Java面试——Redis
优质博文:IT-BLOG-CN 一、Redis 为什么那么快 【1】完全基于内存,绝大部分请求是纯粹的内存操作,非常快速。数据存在内存中。 【2】数据结构简单,对数据操作也简单,Redis中的数据结构是专门进行设计的。 【3】采用单线…...

信号系统之复数傅立叶变换
1 实数DFT 傅里叶变换系列的所有四个成员(DFT、DTFT、傅里叶变换和傅里叶级数)都可以用实数或复数进行。由于DSP主要关心的是DFT,所以就以它为例。 可以根据以下方程定义离散傅里叶变换的实数版本: 一个 N 个样本时域信号 被分解…...

Unity - 相机画面为黑白效果
一、 在Hierarchy中创建一个Global Volume,并设置它为局部作用 二、 将场景出现的作用域范围缩小至相机所在位置,将相机包含即可。 三、添加覆盖组件Color Adjustments,并将Saturation直接拉为-100 。 此时,相机拍摄画面为黑白,场景视图中…...

哈啰Java 春招 24届
时长 1h 3. 为什么使用分布式ID,解决了什么问题 4. Leaf算法了解吗?讲一下原理和工作流程以及优缺点 5. 有没有可能导致id重复?该如何解决? 6. 项目中redis是如何运用的? 7. 项目中分布式锁是如何实现的? 8…...
)
《剑指 Offer》专项突破版 - 面试题 68 : 查找插入位置/ 69 : 山峰数组的顶部(C++ 实现)
目录 面试题 68 : 查找插入位置 面试题 69 : 山峰数组的顶部 面试题 68 : 查找插入位置 题目: 输入一个排序的整数数组 nums 和一个目标指 t,如果数组 nums 中包含 t,则返回 t 在数组中的下标;如果数组 nums 中不包含 t&#…...
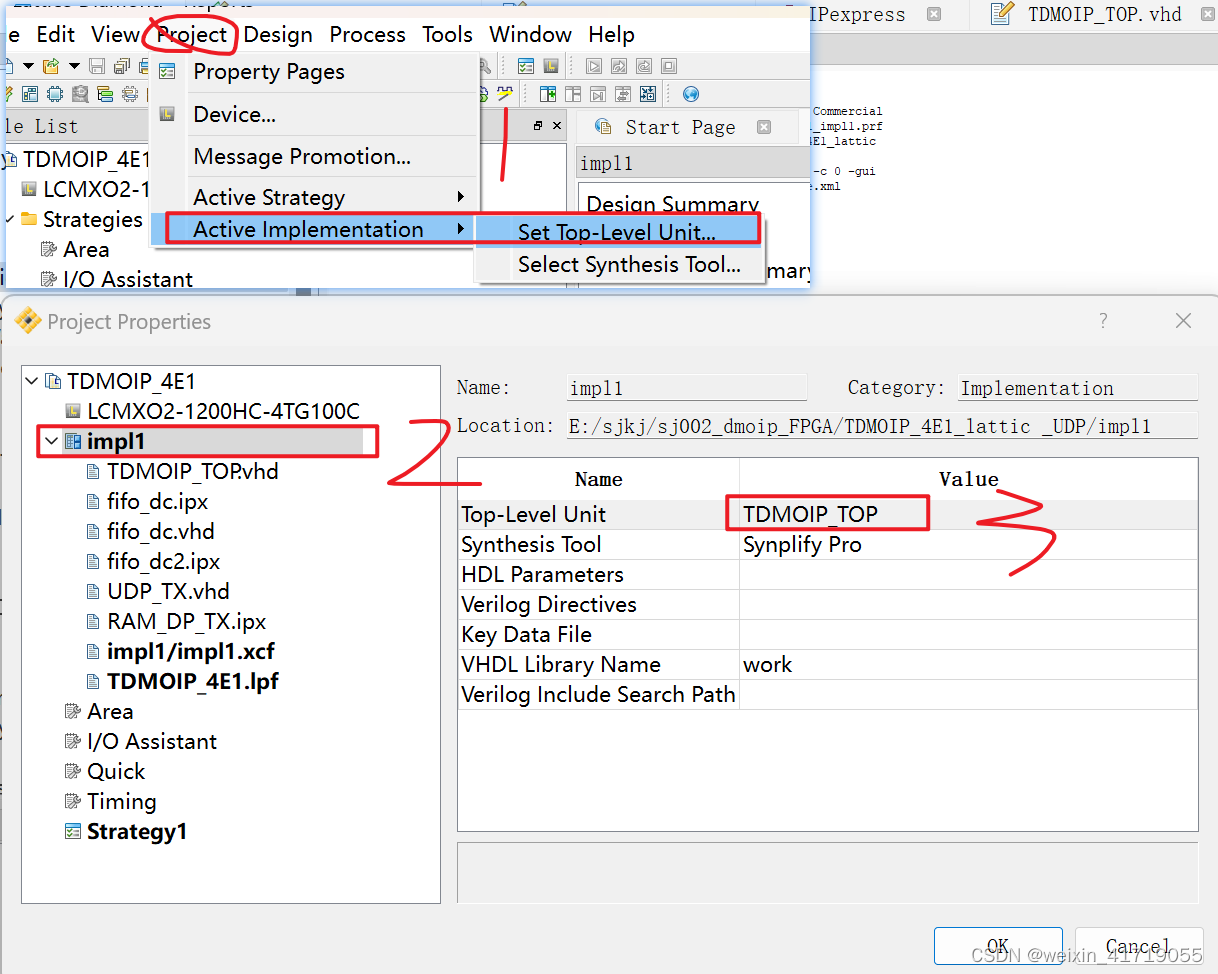
赖迪思软件 lattice Diamond
问题1:工程编译好后,git上传,变更分支又切换回来,再次编译有时候失败,所以配置好的管脚变成默认的,生成的IP核变成名变粗(顶部文件,管脚配置显示IP核输入输出信号配置)。…...
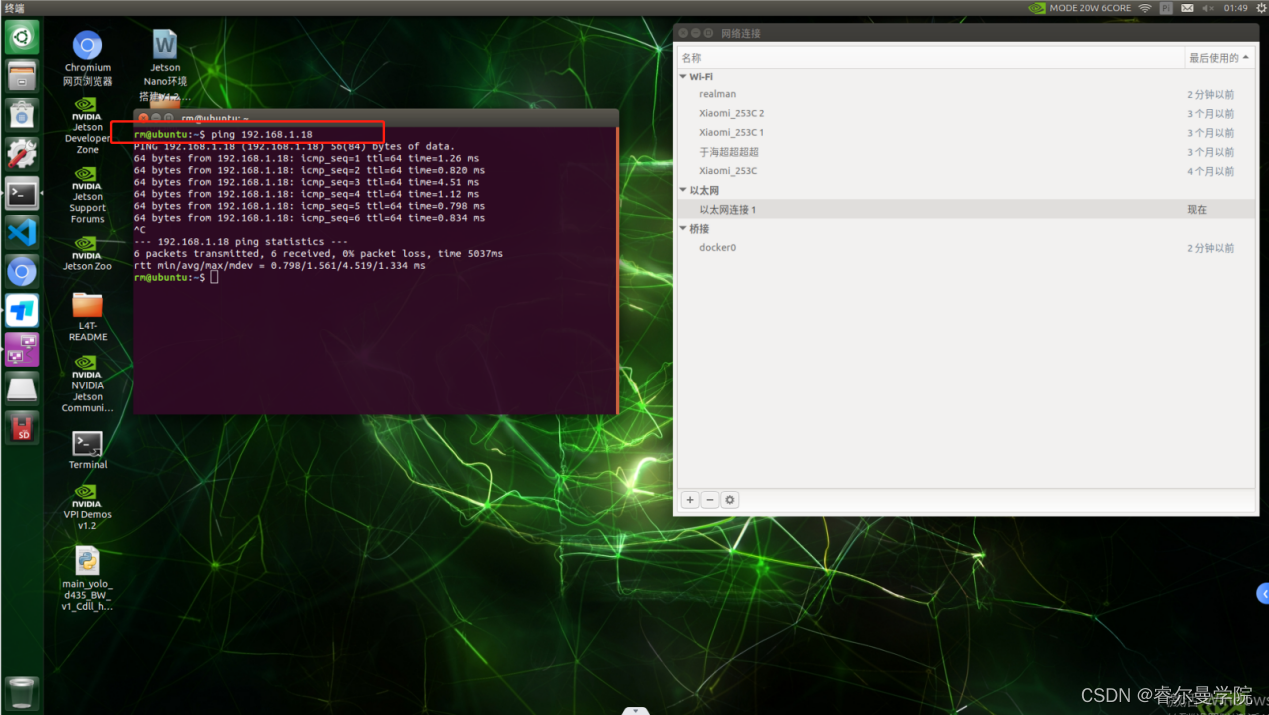
ROS开发基础-Linux基础第四部(开发板设置本地IP)
一 、网线连接设备 使用网线连接jetson NX与机械臂,如下图所示: 二、 修改上位机IPV4 IP ①测试是否可连接。网线连接机械臂之后,在桌面打开终端输入命令“ping 192.168.1.18”,如不可正常通信,可按照下述步骤进行设置。 ②在U…...
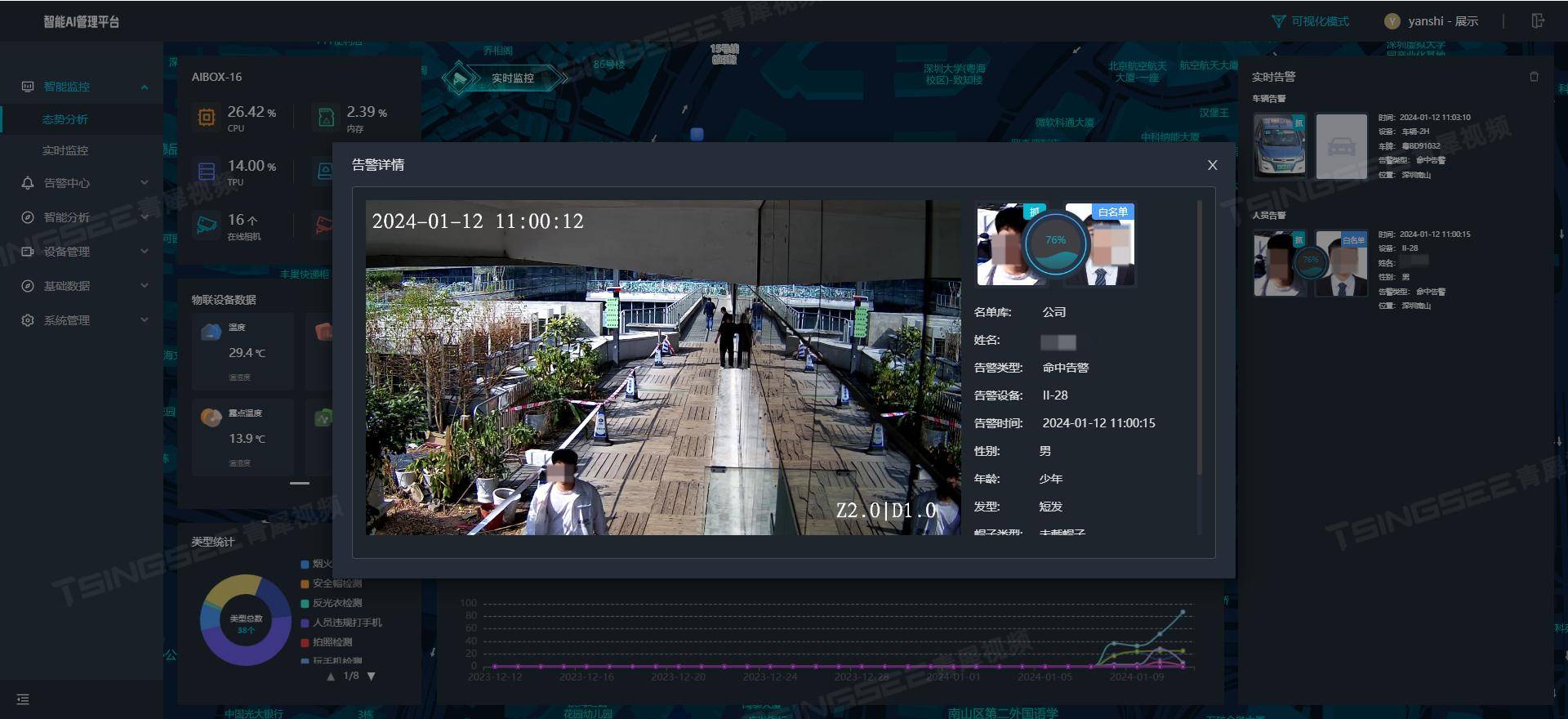
TSINGSEE青犀AI智能分析网关V4智慧油田安全生产监管方案
一、方案背景 随着科技的不断发展,视频监控技术在油田行业中得到了广泛应用。为了提高油田生产的安全性和效率,建设一套智能视频监控平台保障安全生产显得尤为重要。本方案采用先进的视频分析技术、物联网技术、云计算技术、大数据和人工智能技术&#…...

C++基于多设计模式下的同步异步日志系统day3
C基于多设计模式下的同步&异步日志系统day3 📟作者主页:慢热的陕西人 🌴专栏链接:C基于多设计模式下的同步&异步日志系统 📣欢迎各位大佬👍点赞🔥关注🚓收藏,&am…...

Cypher语句查询neo4j数据库教程
文章目录 Cypher介绍执行Cypher语句查询总结 Cypher介绍 NodeMatcher和RelationshipMatcher能够表达的匹配条件相对简单,更加复杂的查询还是需要用Cypher语句来表达。 Py2neo本身支持执行Cypher语句的执行,可以将复杂的查询写成Cypher语句,…...
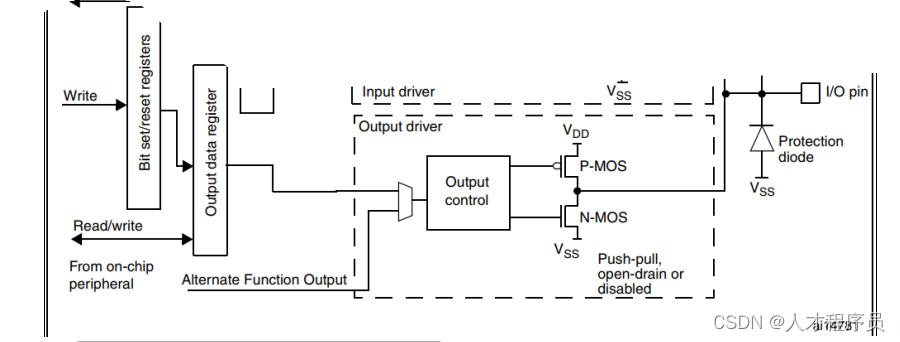
【ESP32 IDF快速入门】点亮第一个LED灯与流水灯
文章目录 前言一、有哪些工作模式?1.1 GPIO的详细介绍1.2 GPIO的内部框图输入模式输出部分 二、GPIO操作函数2.1 GPIO 汇总2.2 GPIO操作函数gpio_config配置引脚reset 引脚函数设置引脚电平选中对应引脚设置引脚的方向 2.3 点亮第一个灯 三、流水灯总结 前言 ESP32…...
再见,Visual Basic——曾经风靡一时的编程语言
2020年3月,微软团队宣布了对Visual Basic(VB)的“终审判决”:不再进行开发或增加新功能。这意味着曾经风光无限的VB正式退出了历史舞台。 VB是微软推出的首款可视化编程软件,自1991年问世以来,便受到了广大…...
【C++精简版回顾】18.文件操作
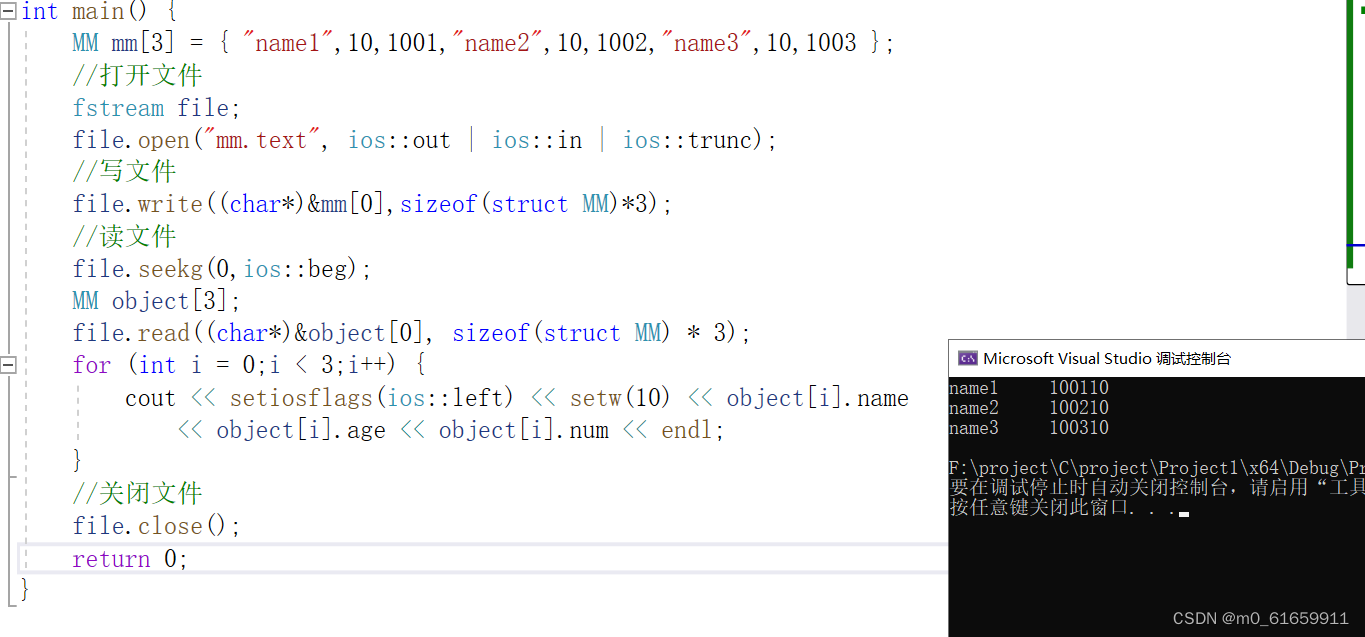
1.文件操作头文件 2.操作文件所用到的函数 1.文件io 1.头文件 #include<fstream> 2.打开文件 (1)函数名 文件对象.open (2)函数参数 /* ios::out 可读 ios::in 可…...
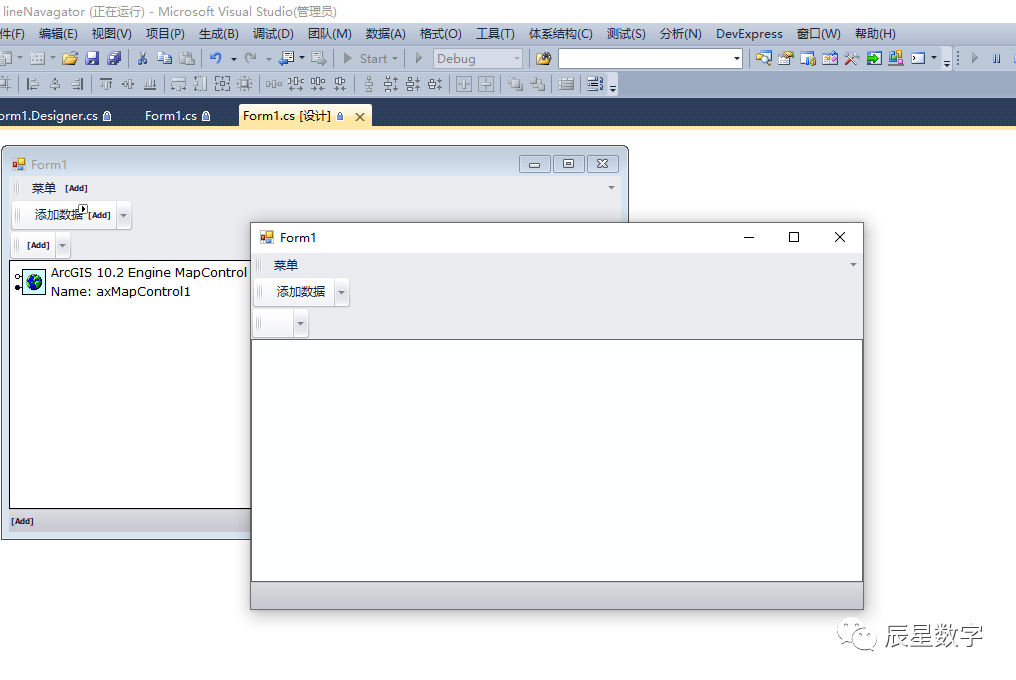
【解决方案】ArcGIS Engine二次开发时,运行后出现“正尝试在 OS 加载程序锁内执行托管代码。不要尝试在 DllMain...”
我们在做ArcGIS Engine二次开发时,特别是新手,安装好了开发环境,满怀信心的准备将按照教程搭建好的框架在Visual Studio中进行运行。点击运行后,却出现了“正尝试在 OS 加载程序锁内执行托管代码。不要尝试在 DllMain 或映像初始化…...
新项目,Linux上一键安装MySQL,Redis,Nacos,Minio
大家好,我是 jonssonyan 分享一个我的一个开源项目,这是一个在 Linux 平台上一键安装各种软件的脚本项目,脚本使用 Shell 语言编写,后续还会增加更多软件的一键安装,代码在 GitHub 上全部开源的,开源地址如…...

Rust 从 PyTorch 到 Burn
一、性能轮盘赌 机器码相同,但放置在不同的地址上,性能可能截然不同。 作为软件开发人员,我们经常假设特定代码的性能仅由代码本身和运行它的硬件决定。这种假设让我们在优化代码以获得更好性能时感到有控制力。虽然在大多数情况下这种假设…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
