基于反光柱特征的激光定位算法思路
目录
- 1. 识别反光柱
- 2. 数据关联
- 2.1 基于几何形状寻找匹配
- 2.2 暴力寻找匹配
- 3. 位姿估计(最小二乘求解)
- 4. 问题
- 4.1 精度问题
- 4.2 快速旋转时定位较差
1. 识别反光柱
反光柱是特殊材料制成,根据激光雷达对反光材料扫描得到的反射值来提取特征。反光柱是圆柱形,我们提取的特征就是反光柱圆心在当前帧下对应激光扫描线束的dist以及angle。提取方法如下:
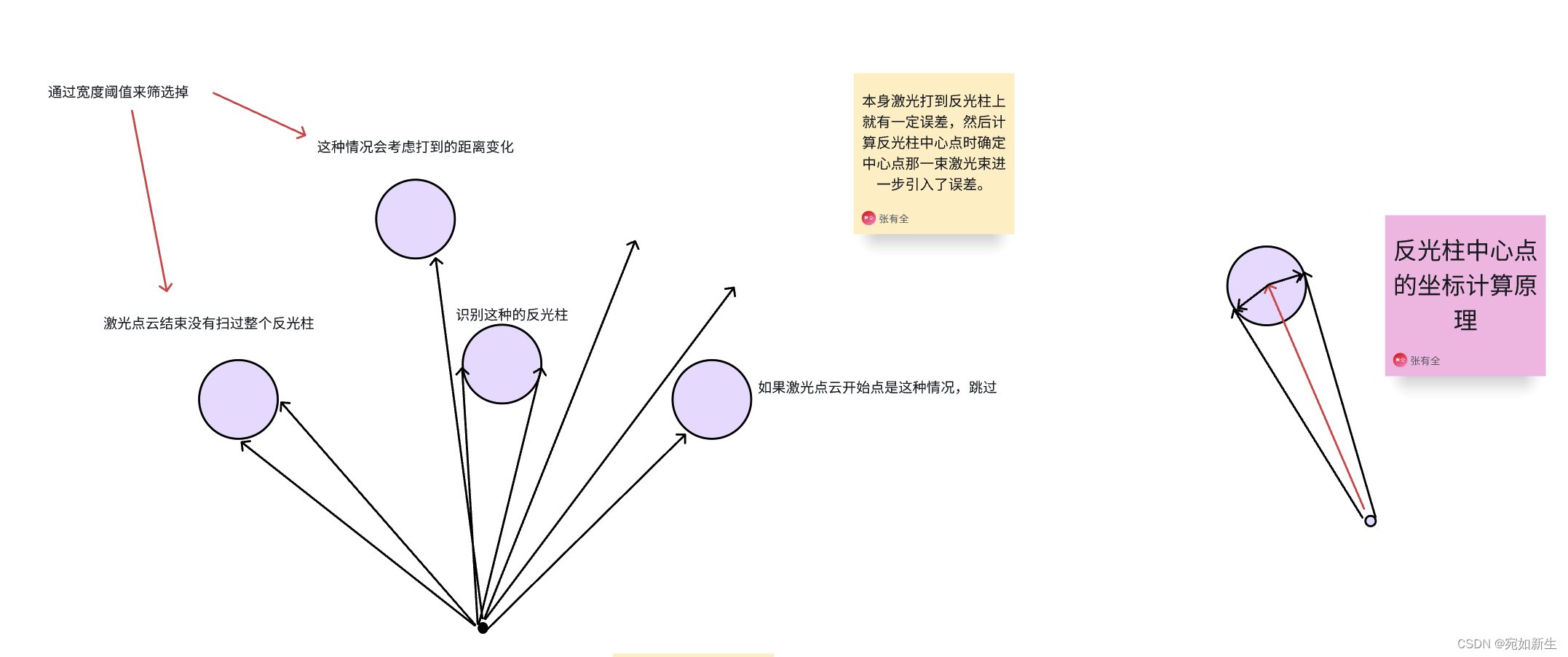
大体思路是,根据激光雷达扫描到反光材料的反射值来确定扫到反光柱开始和结束的两条线束,计算两者之间的夹角,根据三角关系就能算出反光柱圆心到激光雷达的dist和angle。
2. 数据关联
2.1 基于几何形状寻找匹配
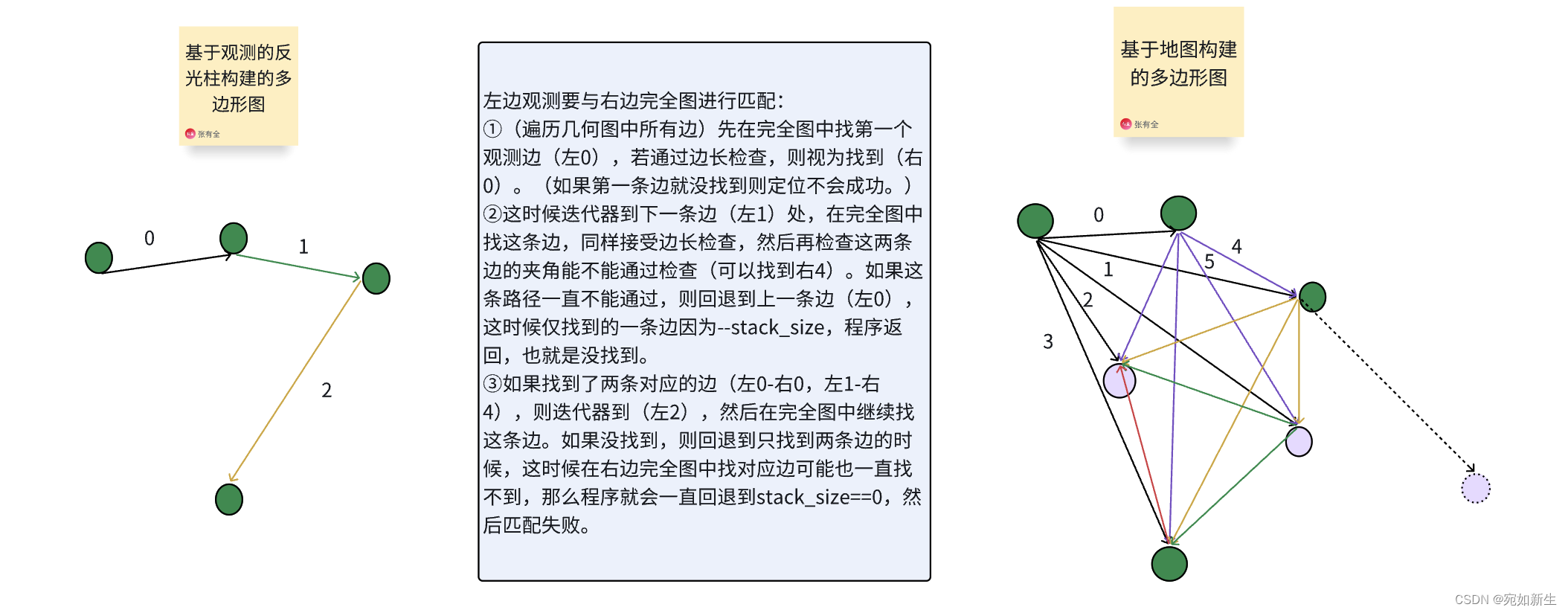
这里用到了一个寻找匹配的技巧。
我们在构建右边完整的多边形图的时候将边长的单位由米转换成了像素。比如我们设定右边多边形图的一个像素代表0.1米,则lidar扫描到的点之间的距离如果是3.132m,在右边图中就是31个像素(int)3.132/0.1。这个像素值作为多边形图中map数据结构的key,在根据真实的边长寻找匹配时,可以快速定位要寻找边的范围,比如3.132m的边在key为[31,32]范围内寻找匹配。
上一步可以认为是粗匹配,接着根据激光雷达的观测精度设置一个精匹配阈值来寻找最接近的边长。(这里反光柱布置较分散时也没有啥影响。)
2.2 暴力寻找匹配

3. 位姿估计(最小二乘求解)
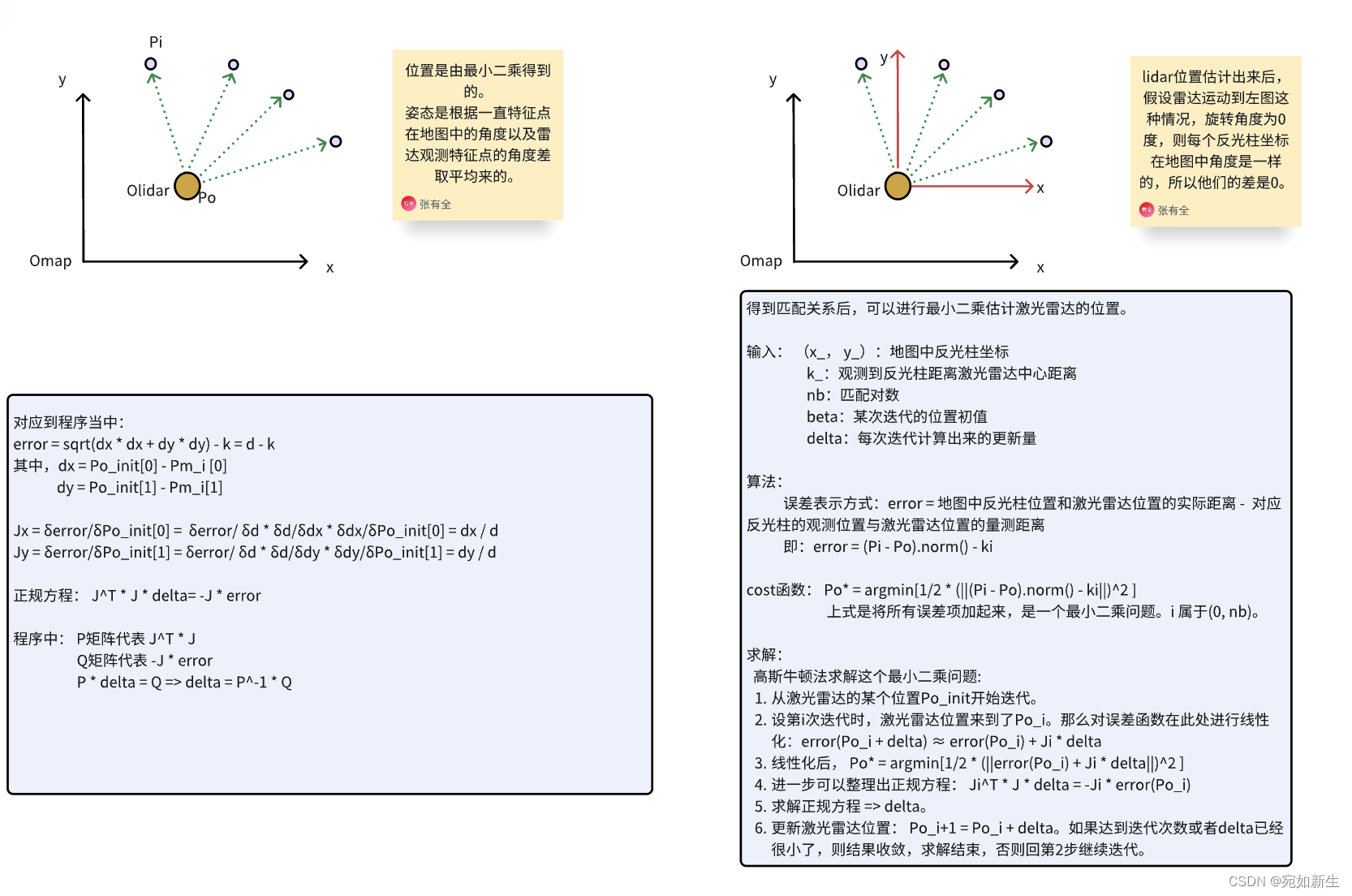
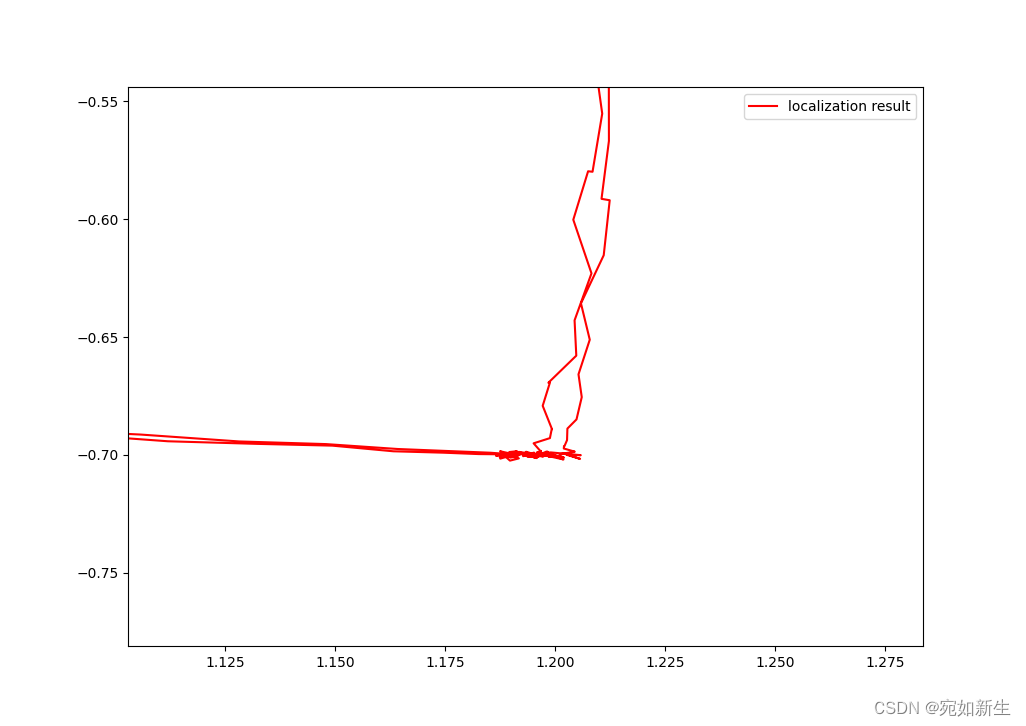
定位结果展示:
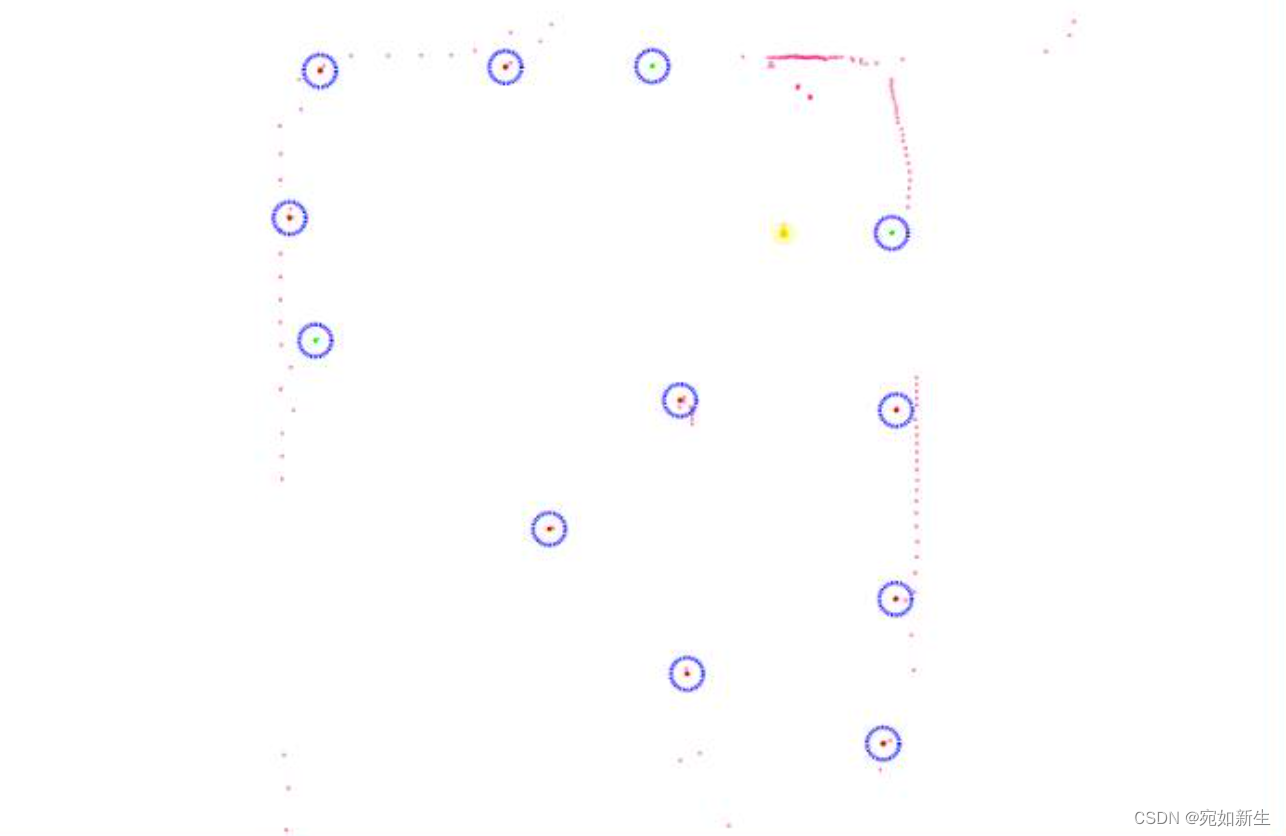
运动轨迹展示:
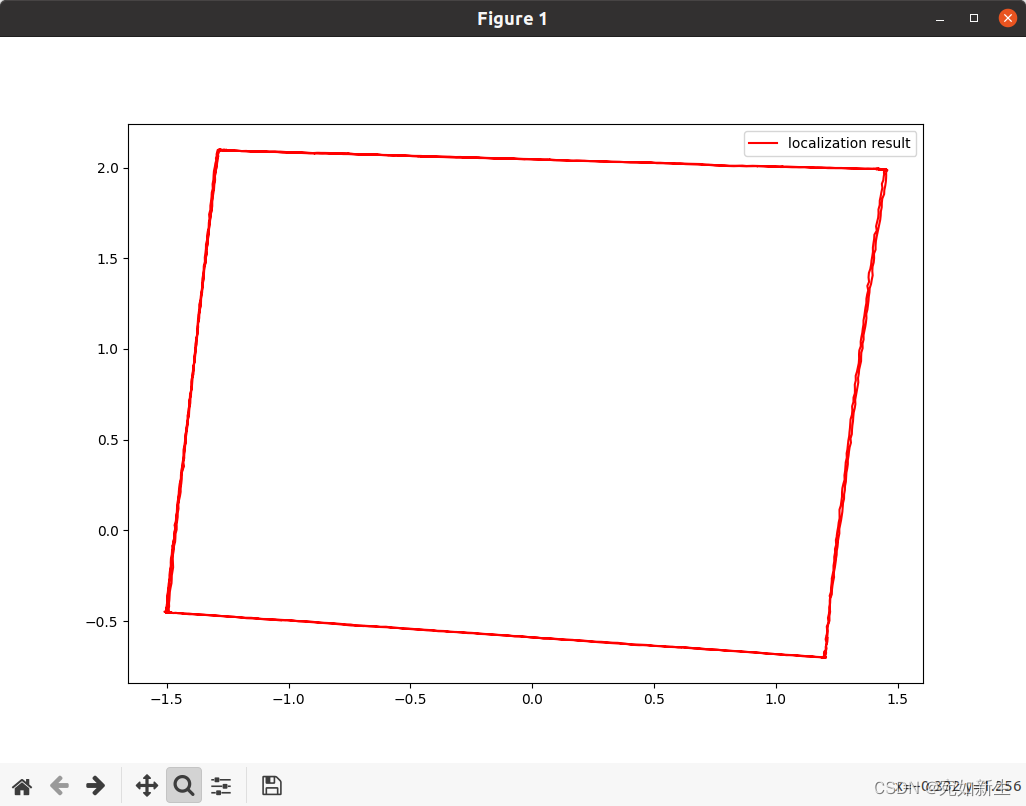
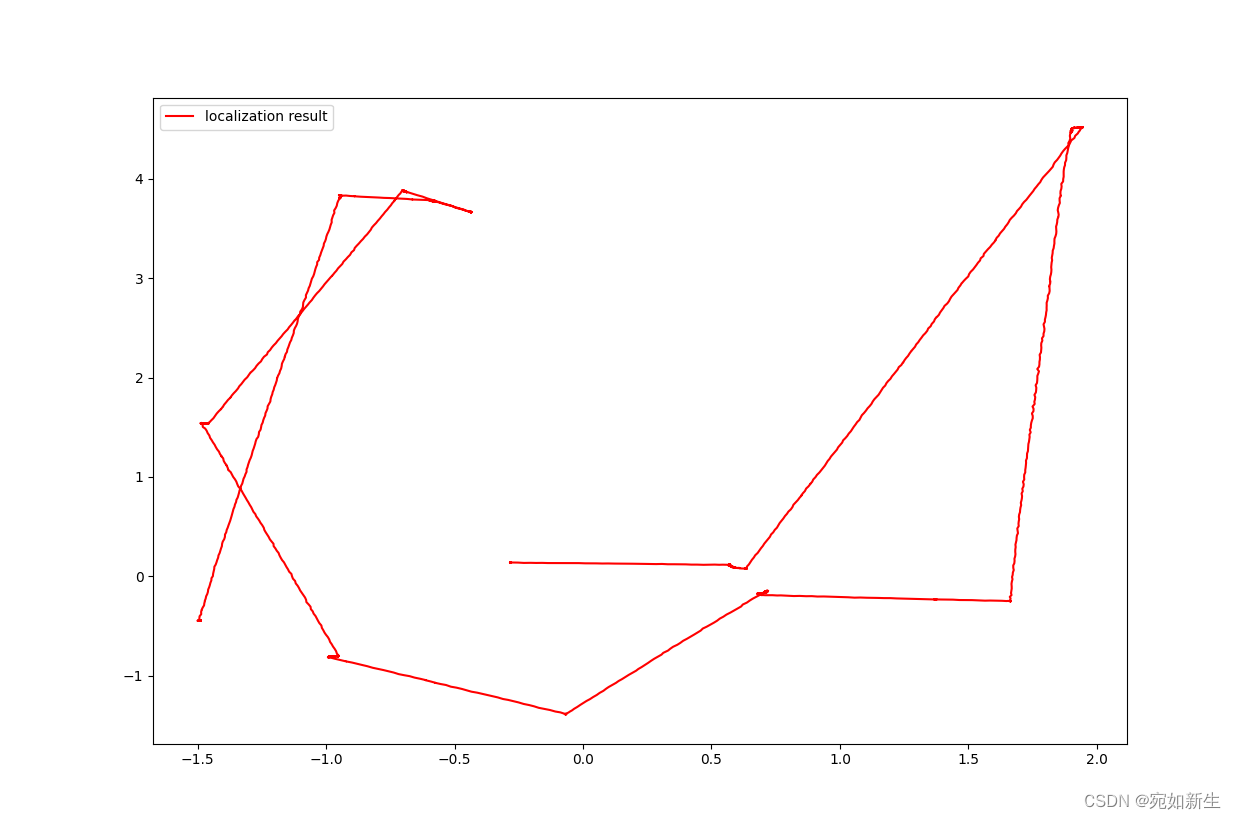
4. 问题
4.1 精度问题
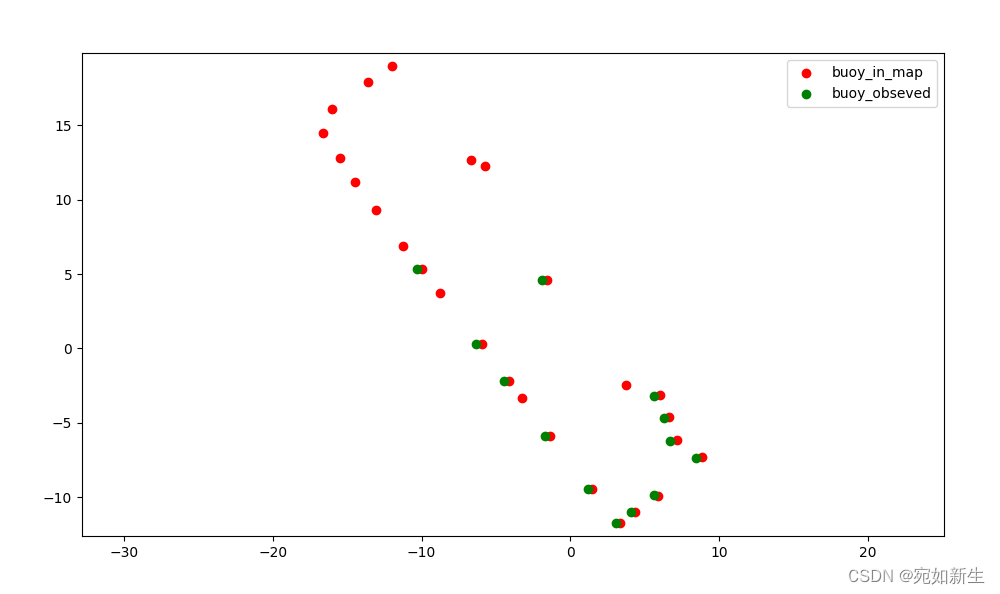
反光柱识别算法精度较差,静止agv,将识别到的反光柱坐标可视化,同一个反光柱,位置应该重合在一处。
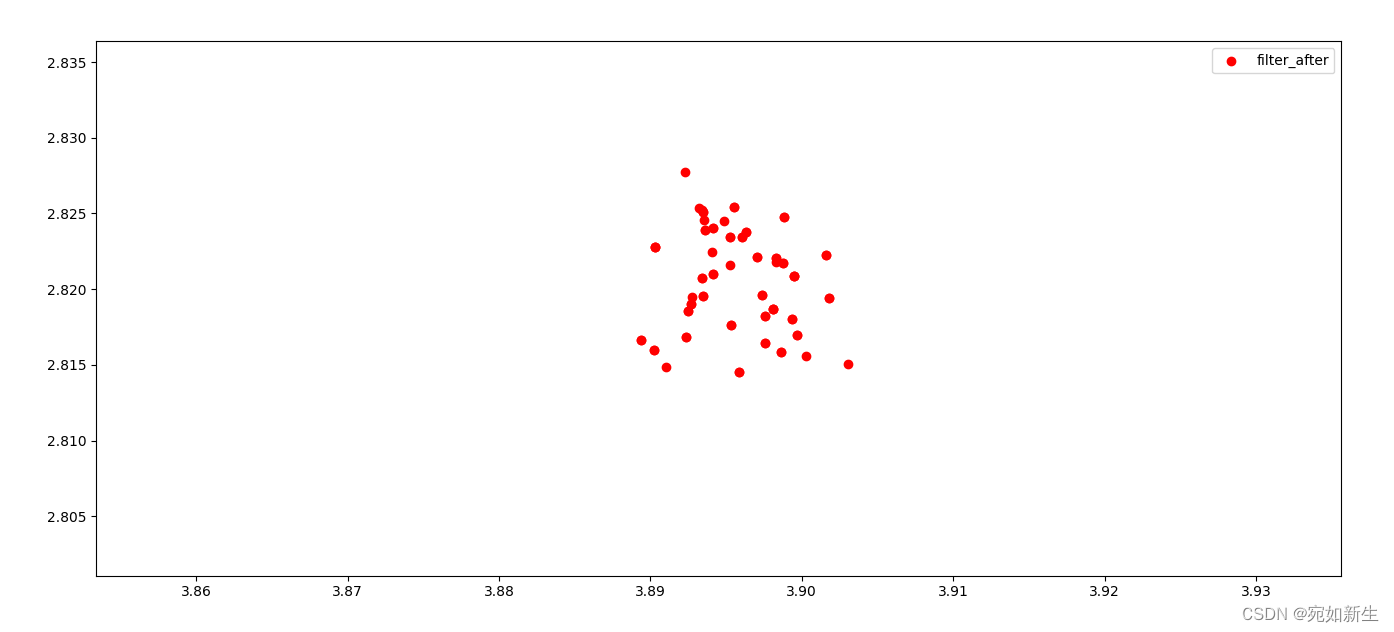
agv静止不动识别反光柱的重复精度在厘米级,这个提取精度会传导到定位上去。从轨迹放大来看在厘米级,可接受。
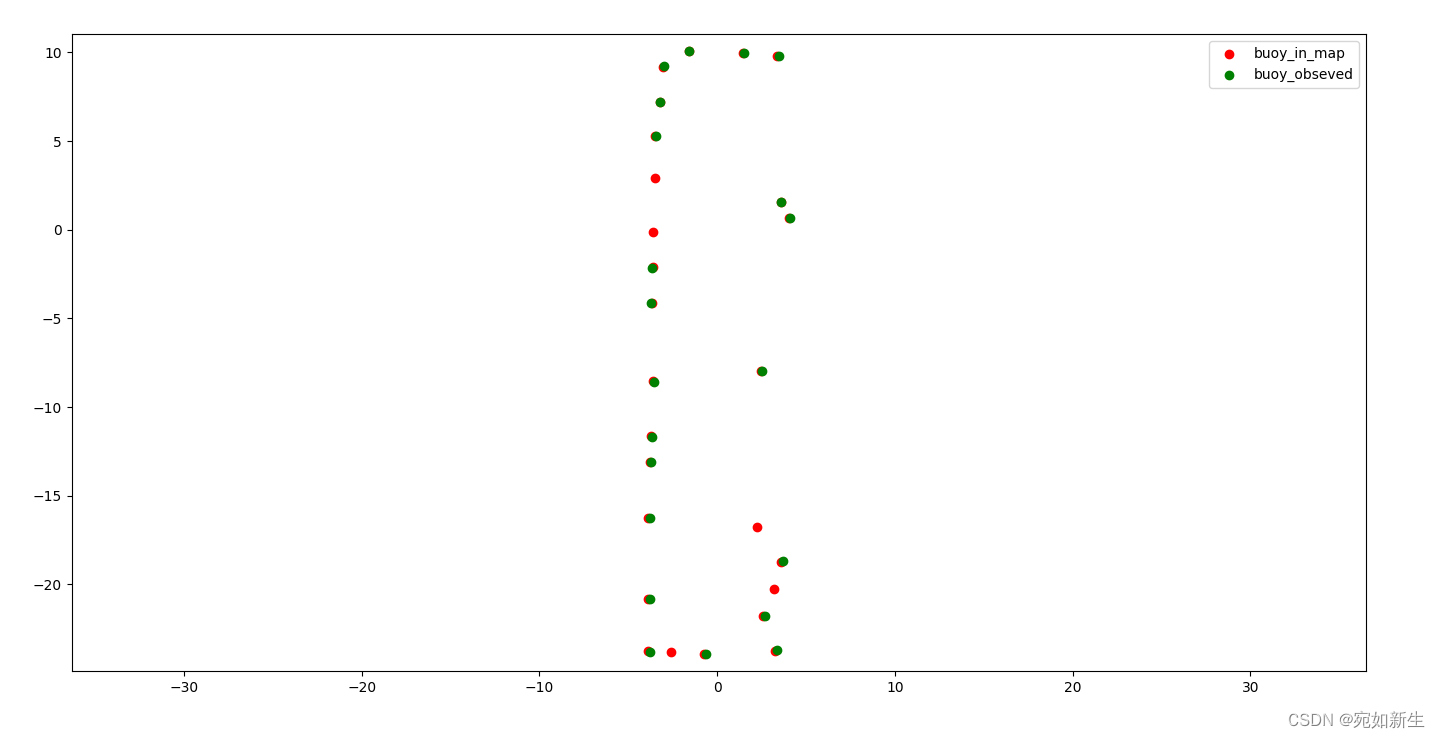
4.2 快速旋转时定位较差
直线行驶较好:
相关文章:

基于反光柱特征的激光定位算法思路
目录 1. 识别反光柱2. 数据关联2.1 基于几何形状寻找匹配2.2 暴力寻找匹配 3. 位姿估计(最小二乘求解)4. 问题4.1 精度问题4.2 快速旋转时定位较差 1. 识别反光柱 反光柱是特殊材料制成,根据激光雷达对反光材料扫描得到的反射值来提取特征。…...

CSM是什么意思?
CSM(Customer Service Management)是企业客户服务管理的信息化(IT)解决方案架构。本着以客户为中心的管理理念,搭建企业客户服务管理平台,实现企业以客户为中心的管理时代的竞争战略。 CSM的核心是以客户为中心,实现对…...

ES6 面试题
1. const、let 和 var 的区别是什么? 答案: var 声明的变量是函数作用域或全局作用域,而 const 和 let 声明的变量是块级作用域。使用 var 声明的变量可以被重复声明,而 const 和 let 不允许重复声明同一变量。const 声明的变量…...
智能指针(C++)
目录 一、智能指针是什么 二、为什么需要智能指针 三、智能指针的使用和原理 3.1、RALL 3.2 智能指针的原理 3.3、智能指针的分类 3.3.1、auto_ptr 3.3.2、unique_ptr 3.3.3、shared_ptr 3.2.4、weak_ptr 一、智能指针是什么 在c中,动态内存的管理式通过一…...

社区店商业模式探讨:如何创新并持续盈利?
在竞争激烈的商业环境中,社区店要想获得成功并持续盈利,需要不断创新和优化商业模式。 作为一名开鲜奶吧5年的创业者,我将分享一些关于社区店商业模式创新的干货和见解,希望能给想开实体店或创业的朋友们提供有价值的参考。 1、…...
一些可以访问gpt的方式
1、Coze扣子是新一代 AI 大模型智能体开发平台。整合了插件、长短期记忆、工作流、卡片等丰富能力,扣子能帮你低门槛、快速搭建个性化或具备商业价值的智能体,并发布到豆包、飞书等各个平台。https://www.coze.cn/ 2、https://poe.com/ 3、插件阿里…...

springer模板参考文献不显示
Spring期刊模板网站,我的问题是23年12月的版本 https://www.springernature.com/gp/authors/campaigns/latex-author-support/see-where-our-services-will-take-you/18782940 参考文献显示问好,在sn-article.tex文件中,这个sn-mathphys-num…...
【【C语言简单小题学习-1】】
实现九九乘法表 // 输出乘法口诀表 int main() {int i 0;int j 0;for (i 1; i < 9; i){for (j 1; j < i;j)printf("%d*%d%d ", i , j, i*j);printf("\n"); }return 0; }猜数字的游戏设计 #define _CRT_SECURE_NO_WARNINGS 1 #include<stdi…...

mongoDB 优化(1)索引
1、创建复合索引(多字段) db.collection_test1.createIndex({deletedVersion: 1,param: 1,qrYearMonth: 1},{name: "deletedVersion_1_param_1_qrYearMonth_1",background: true} ); 2、新增索引前: 执行查询: mb.r…...
stable diffusion webUI之赛博菩萨【秋葉】——工具包新手安裝与使用教程
stable diffusion webUI之赛博菩萨【秋葉】——工具包新手安裝与使用教程 AI浪潮袭来,还是学习学习为妙赛博菩萨【秋葉】简介——(葉ye,四声,同叶)A绘世启动器.exe(sd-webui-aki-v4.6.x)工具包安…...

鸿蒙应用程序包安装和卸载流程
开发者 开发者可以通过调试命令进行应用的安装和卸载,可参考多HAP的调试流程。 图1 应用程序包安装和卸载流程(开发者) 多HAP的开发调试与发布部署流程 多HAP的开发调试与发布部署流程如下图所示。 图1 多HAP的开发调试与发布部署流程 …...

C语言数组全面解析:从初学到精通
数组 1. 前言2. 一维数组的创建和初始化3. 一维数组的使用4. 一维数组在内存中的存储5. 二维数组的创建和初始化6. 二维数组的使用7. 二维数组在内存中的存储8. 数组越界9. 数组作为函数参数10. 综合练习10.1 用函数初始化,逆置,打印整型数组10.2 交换两…...
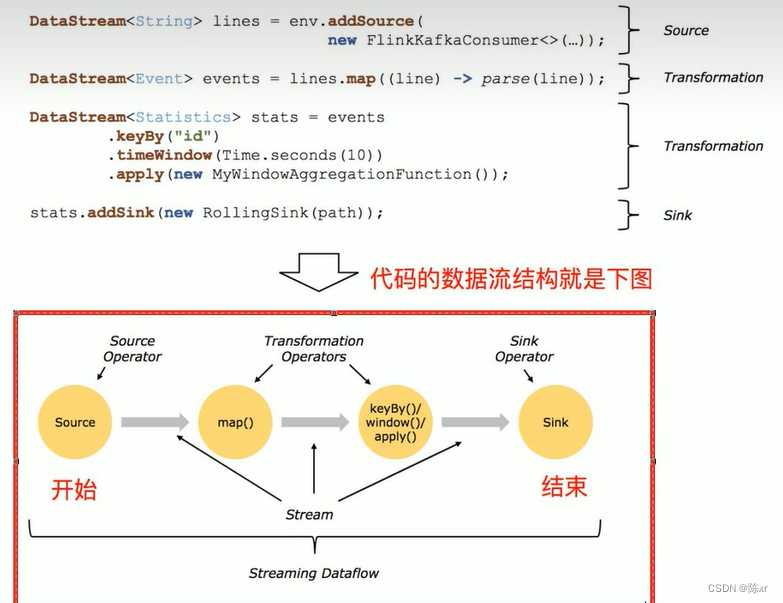
2024-02-28(Kafka,Oozie,Flink)
1.Kafka的数据存储形式 一个主题由多个分区组成 一个分区由多个segment段组成 一个segment段由多个文件组成(log,index(稀疏索引),timeindex(根据时间做的索引)) 2.读数据的流程 …...

Window下编写的sh文件在Linux/Docker中无法使用
Window下编写的sh文件在Linux/Docker中无法使用 一、sh文件目的1.1 初始状态1.2 目的 二、过程与异常2.1 首先获取标准ubuntu20.04 - 正常2.2 启动ubuntu20.04容器 - 正常2.3 执行windows下写的preInstall文件 - 报错 三、检查和处理3.1 评估异常3.2 处理异常3.3 调整后运行测试…...
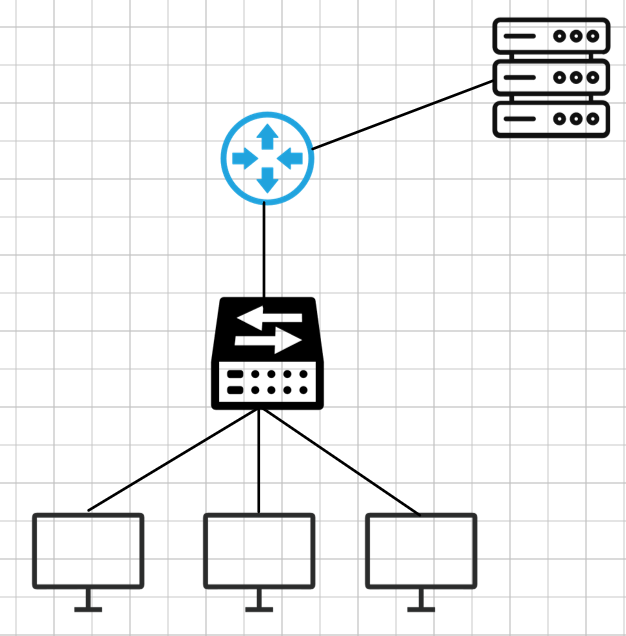
第16章-DNS
目录 1. 域名 1.1 产生背景 1.2 概述 1.3 域名的树形层次化结构 2. DNS 2.1 概述 2.2 工作机制 3. DNS查询模式 3.1 递归查询: 3.2 迭代查询: 4. 相关知识点 4.1 集中式DNS 4.2 国内通用DNS 4.3 配置DNS代理 1. 域名 1.1 产生背景 ① IP…...
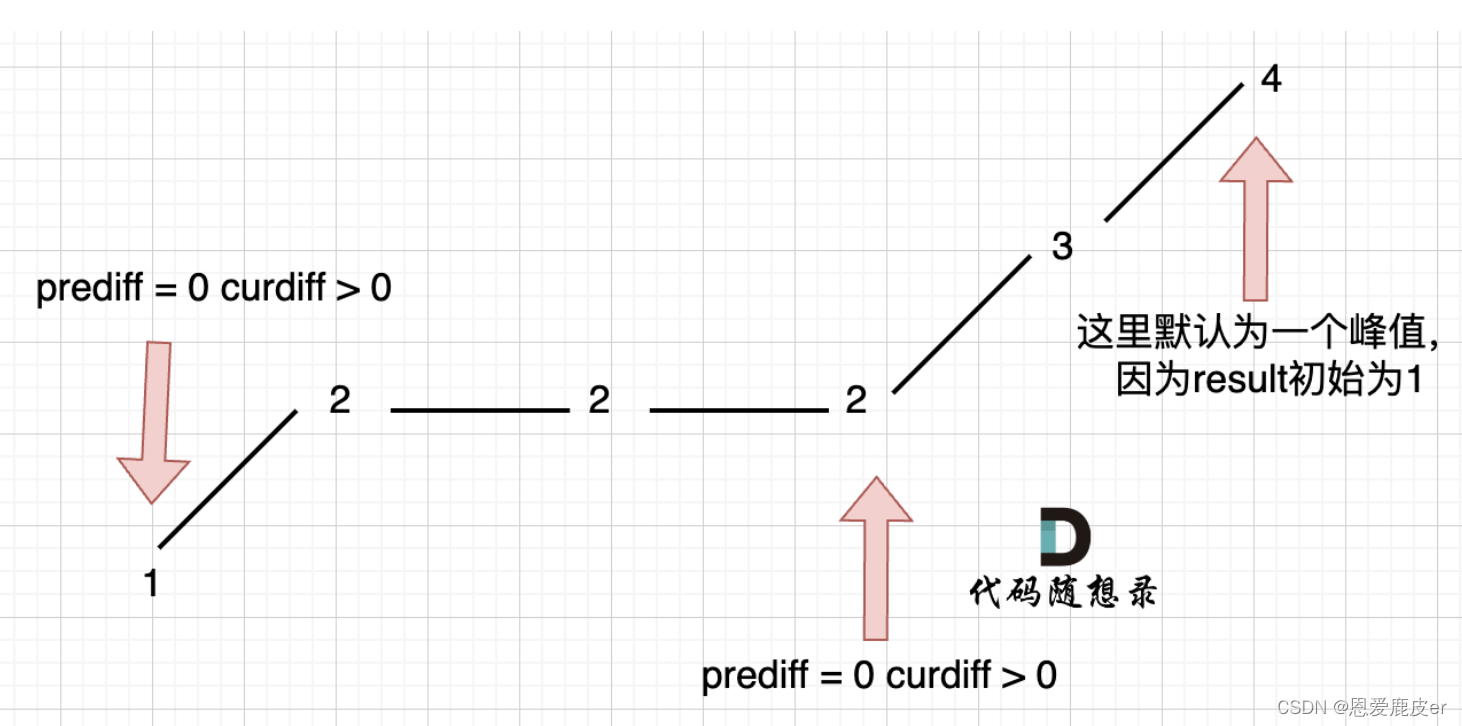
Leetcoder Day27| 贪心算法part01
语言:Java/Go 理论 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 什么时候用贪心?可以用局部最优退出全局最优,并且想不到反例到情况 贪心的一般解题步骤 将问题分解为若干个子问题找出适合的贪心策略求解每一个子…...

SpringBoot自动配置中bean的加载控制
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...

Linux系统运维脚本:根据菜单选择要登录到的Linux主机,方便维护多个linux服务器
目 录 一、要求 二、解决方案 (一)解决思路 (二)方案 三、脚本程序实现 (一)脚本代码和解释 1、定义hosts.txt文件 2、脚本代码 3、代码解释 (二)脚本验证 1…...

蓝桥杯练习题——二分
1.借教室 思路 1.随着订单的增加,每天可用的教室越来越少,二分查找最后一个教室没有出现负数的订单编号 2.每个订单的操作是 [s, t] 全部减去 d #include<iostream> #include<cstring> using namespace std; const int N 1e6 10; int d[…...
Java面试——Redis
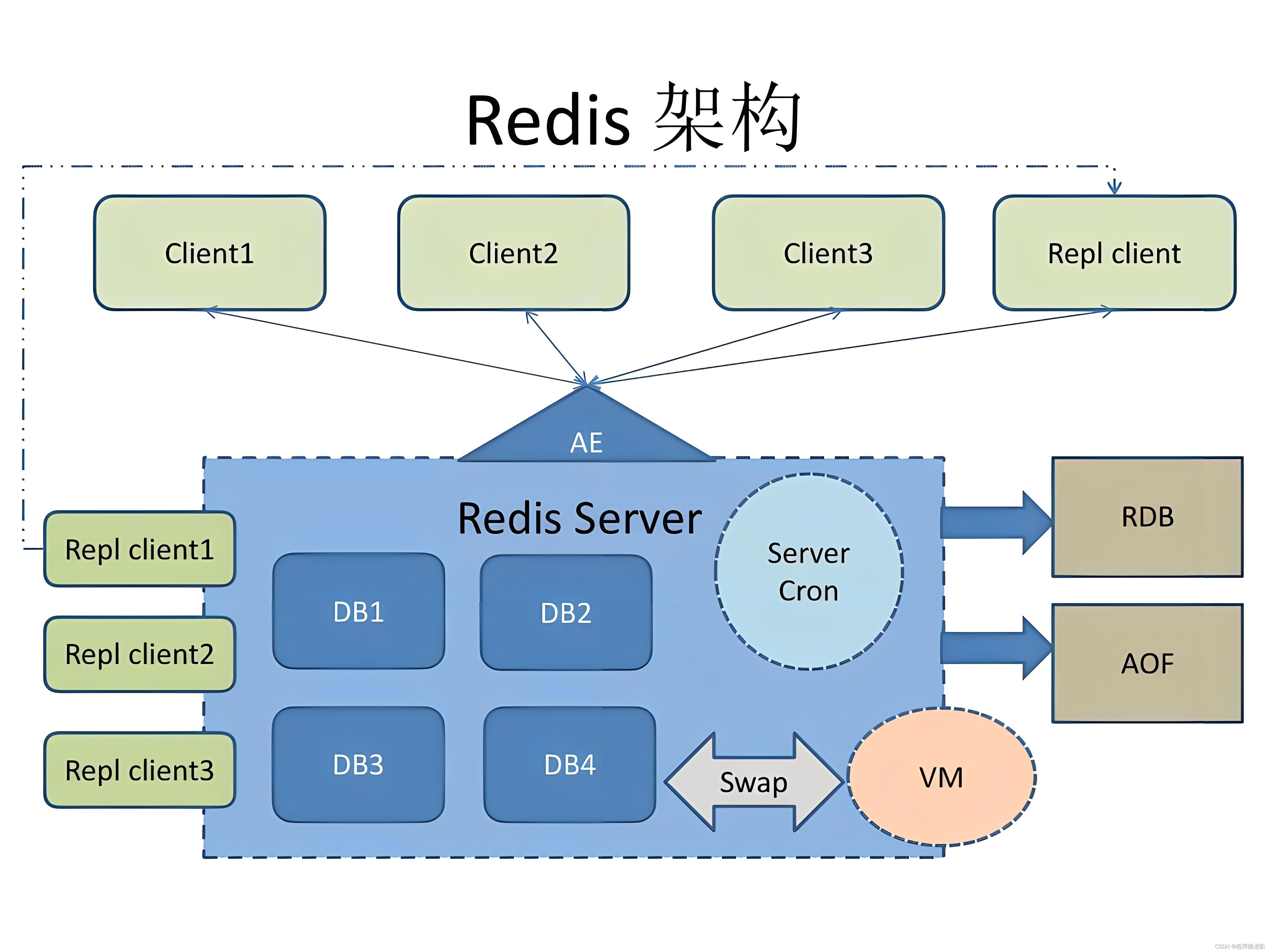
优质博文:IT-BLOG-CN 一、Redis 为什么那么快 【1】完全基于内存,绝大部分请求是纯粹的内存操作,非常快速。数据存在内存中。 【2】数据结构简单,对数据操作也简单,Redis中的数据结构是专门进行设计的。 【3】采用单线…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...