LeetCode受限条件下可到达节点的数目
题目描述
现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 ,共有 n - 1 条边。
给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。
在不访问受限节点的前提下,返回你可以从节点 0 到达的 最多 节点数目。
注意,节点 0 不 会标记为受限节点。
示例 1:
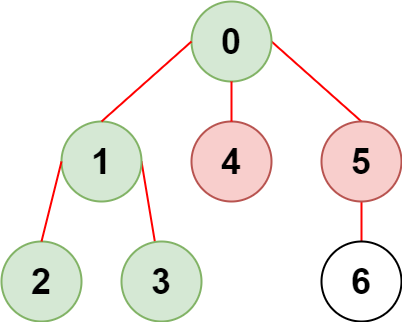
输入:n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5] 输出:4 解释:上图所示正是这棵树。 在不访问受限节点的前提下,只有节点 [0,1,2,3] 可以从节点 0 到达。
示例 2:
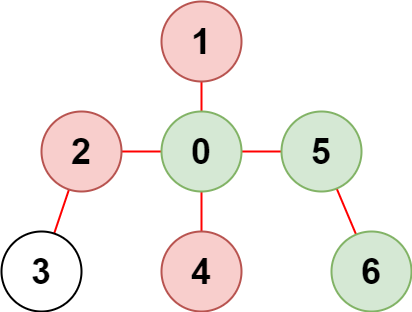
输入:n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1] 输出:3 解释:上图所示正是这棵树。 在不访问受限节点的前提下,只有节点 [0,5,6] 可以从节点 0 到达。
解题思路
本题并不难,解题主要是抓住题意,因为受限节点不可以访问,所以我们可以直接将受限节点涉及到的边直接排除在外,而后在验证节点是否受限时,如果一个个查显然时间复杂度过高,这时我们可以使用Set,减少查询的时间复杂度。而后进行一次dfs就可以了,而后我们还需要知道,因为这是一棵树,所以节点不会重复访问,所以我们直接++即可。
代码如下
class Solution {int cnt=0;public int reachableNodes(int n, int[][] edges, int[] restricted) {Set<Integer> set=new HashSet<Integer>();List<Integer> lists[]=new ArrayList[n];for(int i:restricted)//存入setset.add(i);for(int i=0;i<n;i++)lists[i]=new ArrayList<>();for(int i=0;i<n-1;i++){int x=edges[i][0];int y=edges[i][1];if(set.contains(x)||set.contains(y))//不进行边加入continue;lists[x].add(y);lists[y].add(x);}boolean flag[]=new boolean[n];flag[0]=true;dfs(0,lists,flag);return cnt;}public void dfs(int p,List<Integer> lists[],boolean flag[]){cnt++;//不会重复直接++List<Integer> list=lists[p];for(int i=0;i<list.size();i++){int l=list.get(i);if(!flag[l]){flag[l]=true;dfs(l,lists,flag);flag[l]=false;}}}
}相关文章:

LeetCode受限条件下可到达节点的数目
题目描述 现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 ,共有 n - 1 条边。 给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restr…...
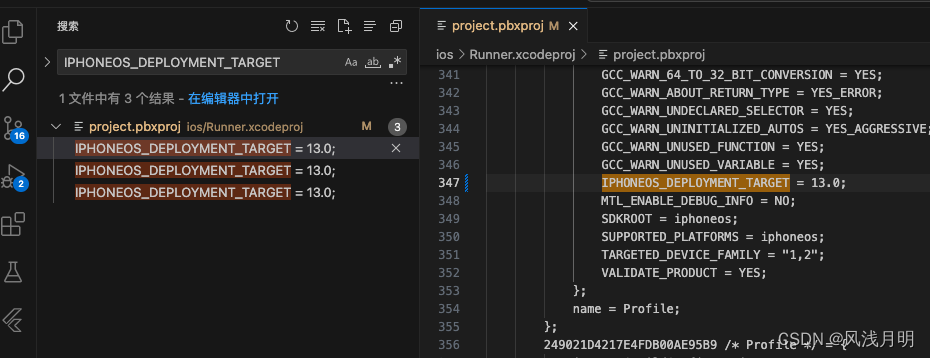
[Flutter]设置应用包名、名称、版本号、最低支持版本、Icon、启动页以及环境判断、平台判断和打包
一、设置应用包名 在Flutter开发中,修改应用程序的包名(也称作Application ID)涉及几个步骤,因为包名是在项目的Android和iOS平台代码中分别配置的。请按照以下步骤操作: 1.Android Flutter工程中全局搜索替换包名 …...
electron-release-server部署electron自动更新服务器记录
目录 一、前言 环境 二、步骤 1、下载上传electron-release-server到服务器 2、宝塔新建node项目网站 3、安装依赖 ①npm install ②安装并配置postgres数据库 ③修改项目配置文件 ④启动项目 ⑤修改postgres的认证方式 ⑥Cannot find where you keep your Bower p…...
贪心(基础算法)--- 区间选点
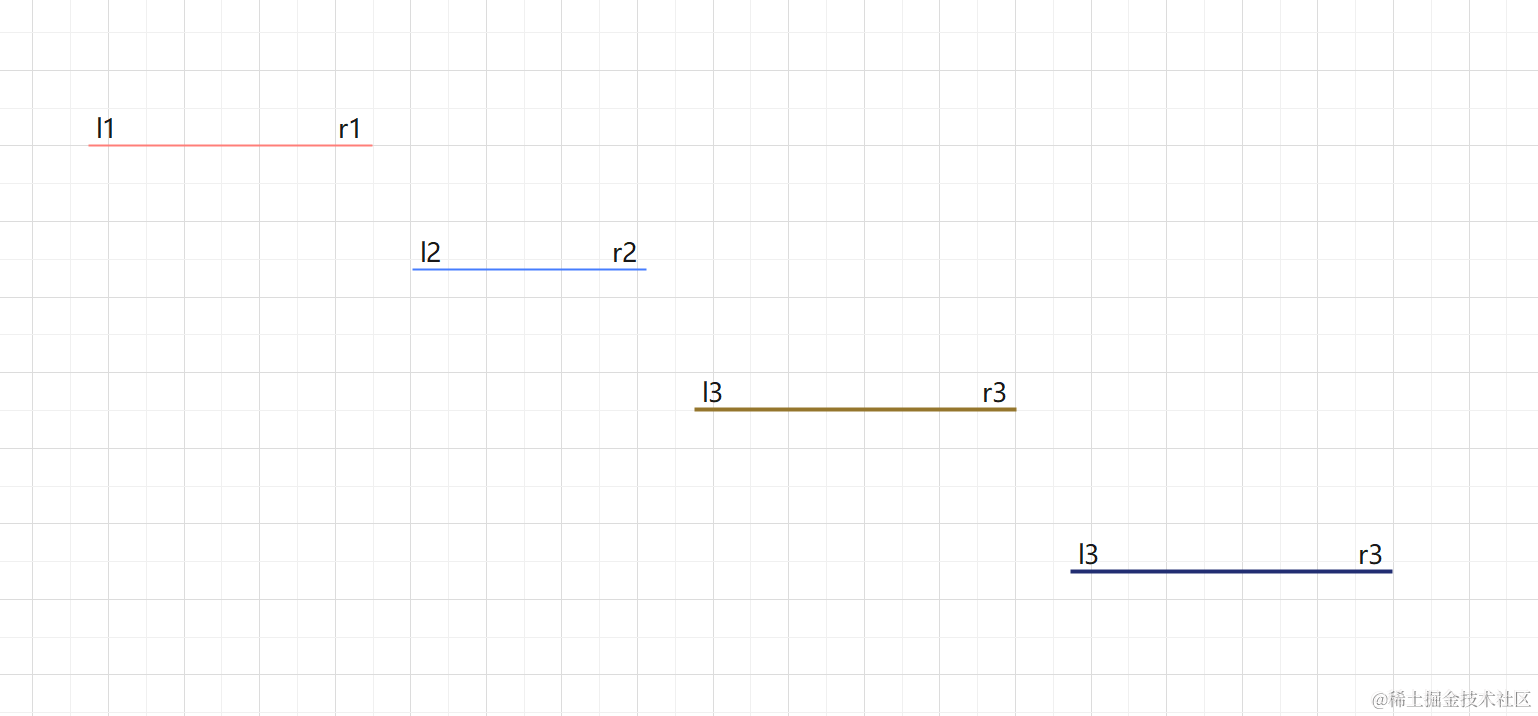
905. 区间选点 思路 (贪心)O(nlogn) 根据右端点排序 将区间按右端点排序 遍历区间,如果当前区间左端点不包含在前一个区间中,则选取新区间,所选点个数加1,更新当前区间右端点。如果包含,则跳…...
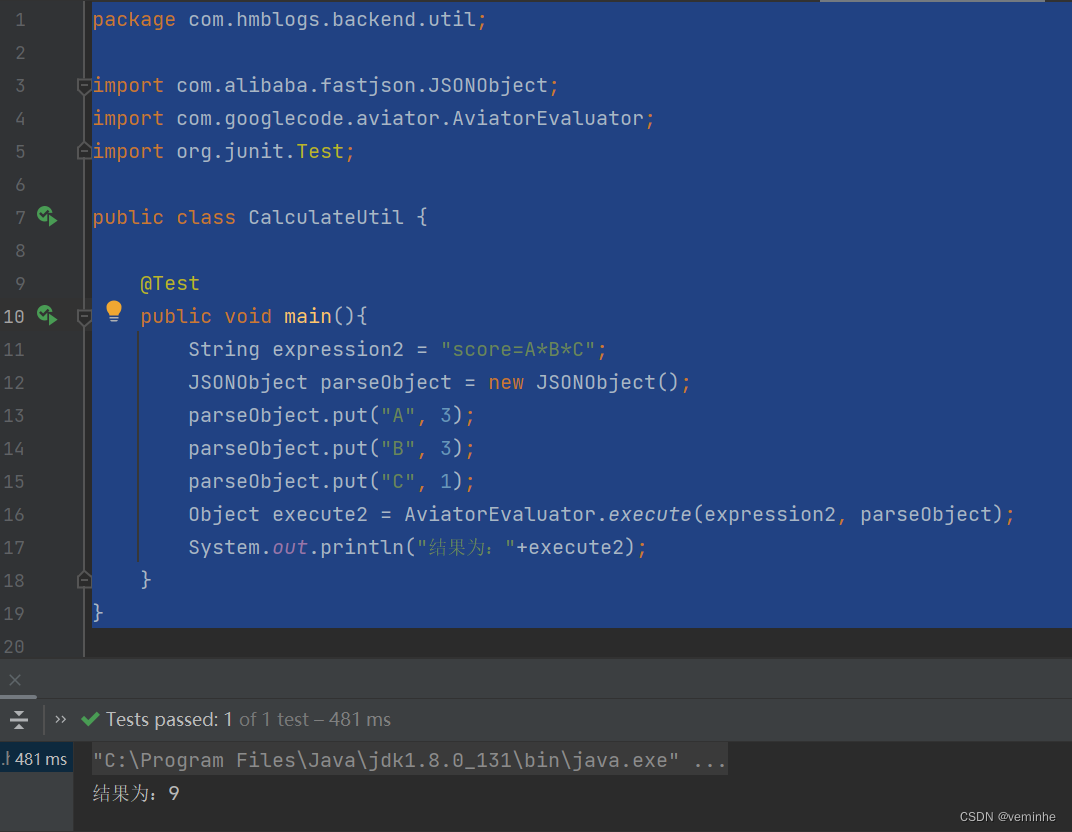
JAVA计算表达式
需求: 1、例如if(score>85){return 1;}else if(score>70){return 2;}else if(score>60){return 3;}else{return 4;}有这一串字符串,要执行这个字符串, 如果score为86分,则能得到1;如果score为30分ÿ…...
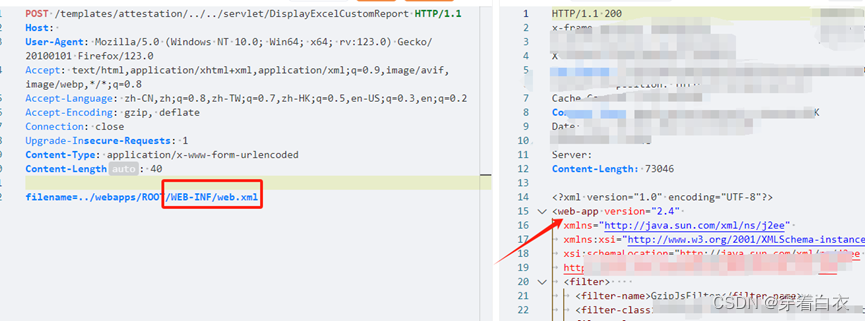
【复现】宏景HCM 任意文件读取漏洞_63
目录 一.概述 二 .漏洞影响 三.漏洞复现 1. 漏洞一: 四.修复建议: 五. 搜索语法: 六.免责声明 一.概述 宏景HCM 将人才标签技术应用于员工招聘、人才选拔等环节,通过多维度的标签体系,形成不同专业序列的人才画…...
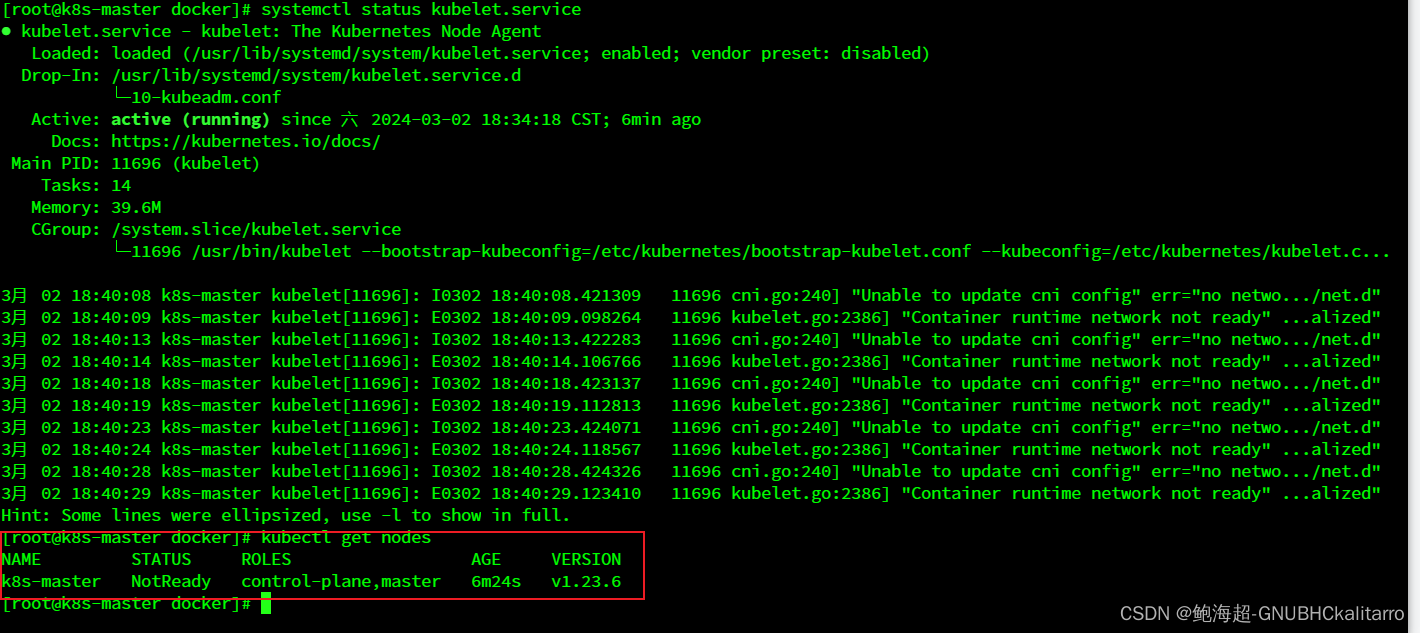
Linux:kubernetes(k8s)搭建mater节点(kubeadm,kubectl,kubelet)(2)
安装k8有多种方式如: minikube kubeadm 二进制安装 命令行工具 我这里就使用kubeadm进行安装 环境 3台centos7 master ip :192.168.113.120 2G运存 2内核 node1 ip :192.168.113.121 2G运存 2内核 node2 ip :192.168.1…...

Web应用安全威胁与防护措施
本文已收录至《全国计算机等级考试——信息 安全技术》专栏 由于极其容易出现漏洞、并引发安全事故,因此数据隐私的保护是目前绝大多数企业不可绕过的运维环节。不过,许多中小型企业往往会错误地认为只有大型企业才会成为黑客的目标。而实际统计数字却截…...

MySQL相关知识汇总
MySQL是一个广泛使用的开源关系型数据库管理系统,它以其高性能、稳定性和易用性而备受开发者喜爱。在软件开发领域,无论是大型项目还是小型应用,MySQL都扮演着重要的角色。本文将对MySQL的一些关键知识点进行汇总,帮助读者更好地了…...

【旧文搬运】为你的 Laravel 应用添加一个基于 Swoole 的 WebSocket 服务
做了一个基于 Swoole 的 WebSocket 扩展包,可以用来做实时状态推送,或者自定义消息处理实现 im,有需要的可以看看: [giorgio-socket] 使用方法 安装 安装扩展包 composer require wu/giorgio-socket发布配置文件 php artisan vendor:pu…...
vue项目从后端下载文件显示进度条或者loading
//API接口 export const exportDownload (params?: Object, peCallback?: Function) > {return new Promise((resolve, reject) > {axios({method: get,url: ,headers: {access_token: ${getToken()},},responseType: blob,params,onDownloadProgress: (pe) > {peC…...
[技巧]Arcgis之图斑四至点批量计算
前言 上一篇介绍了arcgis之图斑四至范围计算,这里介绍的图斑四至点的计算及获取,两者之间还是有差异的。 [技巧]Arcgis之图斑四至范围计算 这里说的四至点指的是图斑最东、最西、最南、最北的四个地理位置点坐标,如下图: 四至点…...

【java】20:枚举
枚举的二种实现方式 1) 自定义类实现枚举 2) 使用 enum 关键字实现枚举 自定义实现枚举: 1.不需要提供setXxx方法,因为枚举对象值通常为只读. 2.对枚举对象/属性使用final static共同修饰,实现底层优化. 3.枚举对象名通常使用全部大写&…...
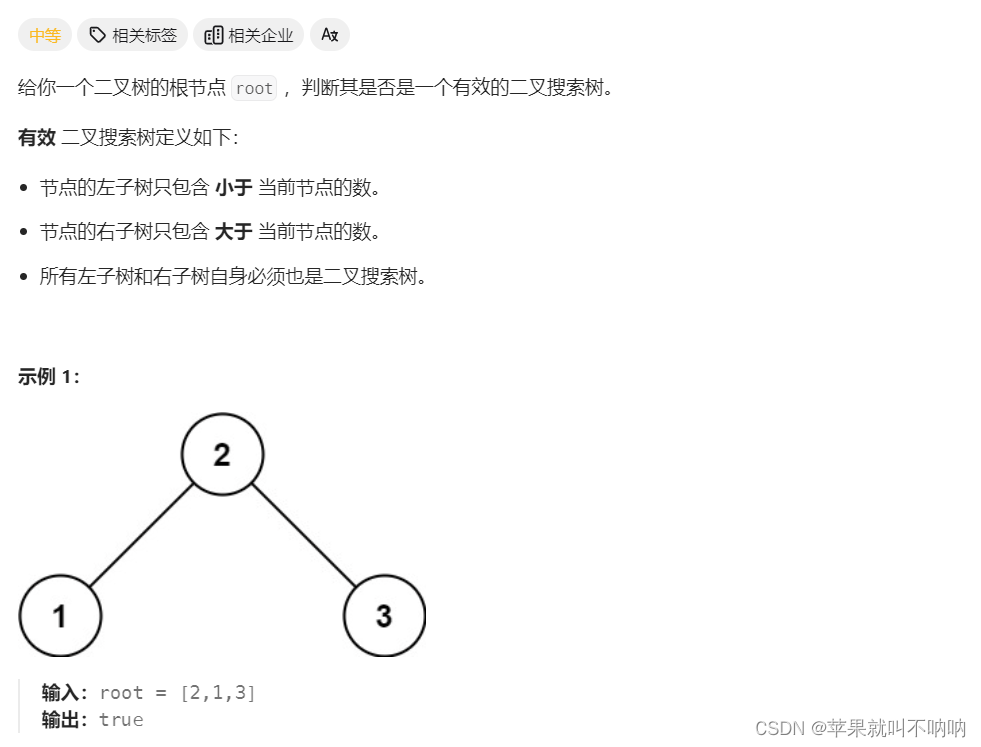
★【二叉搜索树(中序遍历特性)】【 ★递归+双指针】Leetcode 98. 验证二叉搜索树
★【二叉搜索树(中序遍历特性)】【 ★递归双指针】Leetcode 98. 验证二叉搜索树 二叉搜索树 98. 验证二叉搜索树解法1 笨 中序递归遍历为一个数组 然后判断数组是不是升序排列就可以★解法2 不使用数组 递归法 ---------------🎈Ἰ…...
方法实战指南)
打造无缝滚动体验:JavaScript中的scrollIntoView()方法实战指南
在现代Web开发中,提升用户体验是至关重要的。通过JavaScript的scrollIntoView()方法,我们可以为用户创造出流畅而令人愉悦的滚动体验。本文将深入研究scrollIntoView()的强大功能,并结合实例演示如何在项目中巧妙应用,以打造出无缝…...

实战:如何将Oracle单实例数据库转换成Oracle RAC数据库
导读 本文介绍如何将Oracle单实例数据库转换成Oracle RAC数据库 环境说明: 数据库节点2上有个单实例数据库zlxdb2,现在要将zlxdb2转换成RAC数据库,RAC数据库的两个实例分别是lzydb1和lzydb2。 以下是详细的操作步骤: 1、查看zlxdb…...

基于华为atlas的分类模型实战
分类模型选用基于imagenet训练的MobileNetV3模型,分类类别为1000类。 pytorch模型导出为onnx: 修改mobilenetv3.py中网络结构,模型选用MobileNetV3_Small模型,网络输出节点增加softmax层,将原始的return self.linear4…...

编程语言:SQL Server数据库使用教程,SQL Server增删改查语句
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「推荐专栏」:对网络安全感兴趣的小伙伴可以关注专栏《网络安全自学教程》 SQL Server是微软提供的一种关系型数据库,…...

【tableau学习笔记】tableau无法连接数据源
【tableau学习笔记】tableau无法连接数据源 背景: 学校讲到Tableau,兴奋下载Kaggle Excel,一看后缀CSV,导入Tableau发现报错“tableau无法连接数据源”,自作聪明改为后缀XLSX,bug依旧。 省流:…...
cetos7 Docker 安装 gitlab
一、gitlab 简单介绍和安装要求 官方文档:https://docs.gitlab.cn/jh/install/docker.html 1.1、gitlab 介绍 gitLab 是一个用于代码仓库管理系统的开源项目,使用git作为代码管理工具,并在此基础上搭建起来的Web服务平台,通过该平…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

linux设备重启后时间与网络时间不同步怎么解决?
linux设备重启后时间与网络时间不同步怎么解决? 设备只要一重启,时间又错了/偏了,明明刚刚对时还是对的! 这在物联网、嵌入式开发环境特别常见,尤其是开发板、树莓派、rk3588 这类设备。 解决方法: 加硬件…...

SFTrack:面向警务无人机的自适应多目标跟踪算法——突破小尺度高速运动目标的追踪瓶颈
【导读】 本文针对无人机(UAV)视频中目标尺寸小、运动快导致的多目标跟踪难题,提出一种更简单高效的方法。核心创新在于从低置信度检测启动跟踪(贴合无人机场景特性),并改进传统外观匹配算法以关联此类检测…...

可下载旧版app屏蔽更新的app市场
软件介绍 手机用久了,app越来越臃肿,老手机卡顿成常态。这里给大家推荐个改善老手机使用体验的方法,还能帮我们卸载不需要的app。 手机现状 如今的app不断更新,看似在优化,实则内存占用越来越大,对手机性…...

【前端实战】如何让用户回到上次阅读的位置?
目录 【前端实战】如何让用户回到上次阅读的位置? 一、总体思路 1、核心目标 2、涉及到的技术 二、实现方案详解 1、基础方法:监听滚动,记录 scrollTop(不推荐) 2、Intersection Observer 插入探针元素 3、基…...

World-writable config file /etc/mysql/mysql.conf.d/my.cnf is ignored
https://stackoverflow.com/questions/53741107/mysql-in-docker-on-ubuntu-warning-world-writable-config-file-is-ignored 修改权限 -> 重启mysql # 检查字符集配置 SHOW VARIABLES WHERE Variable_name IN (character_set_server, character_set_database ); --------…...
