40. 组合总和 II(力扣LeetCode)
文章目录
- 40. 组合总和 II
- 题目描述
- 回溯算法
40. 组合总和 II
题目描述
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
提示:
- 1 <= candidates.length <= 100
- 1 <= candidates[i] <= 50
- 1 <= target <= 30
回溯算法
// 定义一个Solution类,用于解决组合总和II问题
class Solution {
public:// 定义一个公共方法combinationSum2,它接受一个整数数组candidates和一个整数target,// 返回一个二维整数数组,里面包含了所有可以使数字和为target的组合。vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {// 首先对数组进行排序,这会帮助我们更容易地找到组合,并且能够跳过重复的组合sort(candidates.begin(),candidates.end());// 输出排序后的数组元素,这一步通常是为了调试for(int i=0;i<candidates.size();i++)cout<<candidates[i]<<" ";// 定义一个布尔向量used,用于标记candidates中的元素是否被用在当前的组合中vector<bool> used(candidates.size(),false);// 调用backstracking函数,开始回溯算法backstracking(candidates, target, 0, 0, used);// 返回所有找到的组合return result;}private:// 定义一个私有变量result,用于存储所有找到的组合vector<vector<int>> result;// 定义一个私有变量path,用于存储当前正在考虑的组合vector<int> path;// 定义一个私有函数backstracking,它实现了回溯算法void backstracking(vector<int>& candidates,int target,int sum,int start,vector<bool>& used){// 如果当前组合的数字和大于目标数target,则当前路径不可能为解,回溯if(sum>target)return;// 如果当前组合的数字和等于目标数target,则找到了一个解,将它添加到result中if(sum==target){result.push_back(path);return;}// 从start开始遍历candidates数组,尝试每个可能的元素for(int i=start;i<candidates.size();i++){// 跳过重复的数字,以避免重复的组合,这是因为数组已经排序if(i>0 && candidates[i]==candidates[i-1] && !used[i-1])continue;// 将candidates[i]添加到当前路径path.push_back(candidates[i]);// 标记该元素为已使用used[i]=true;// 将candidates[i]的值加到当前和上,并递归调用backstracking,注意新的start是i+1,因为每个数字只能使用一次sum+=candidates[i];backstracking(candidates, target, sum, i+1, used);// 回溯,将最后一个元素从路径中删除并从当前和中减去,取消标记该元素path.pop_back();used[i]=false;// 从当前和中减去candidates[i]的值,为下一次迭代准备sum-=candidates[i];}}
};代码主要由以下几个部分组成:
- combinationSum2 公共方法:对给定数组排序,初始化用于记录元素使用情况的布尔向量,开始回溯搜索,最后返回结果。
- backstracking 私有方法:实现了回溯算法的核心逻辑,通过递归尝试每个可能的元素,直到找到所有的组合或者终止搜索。
- result 和 path 私有变量:分别用于存储找到的所有组合结果和当前递归路径中的组合。
- used 布尔向量:用于标记数组 candidates 中的元素是否已经被使用过,以防止在同一路径中重复使用。
相关文章:
)
40. 组合总和 II(力扣LeetCode)
文章目录 40. 组合总和 II题目描述回溯算法 40. 组合总和 II 题目描述 给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。 注意ÿ…...
Ubuntu上Jenkins自动化部署Gitee上SpringBoot项目
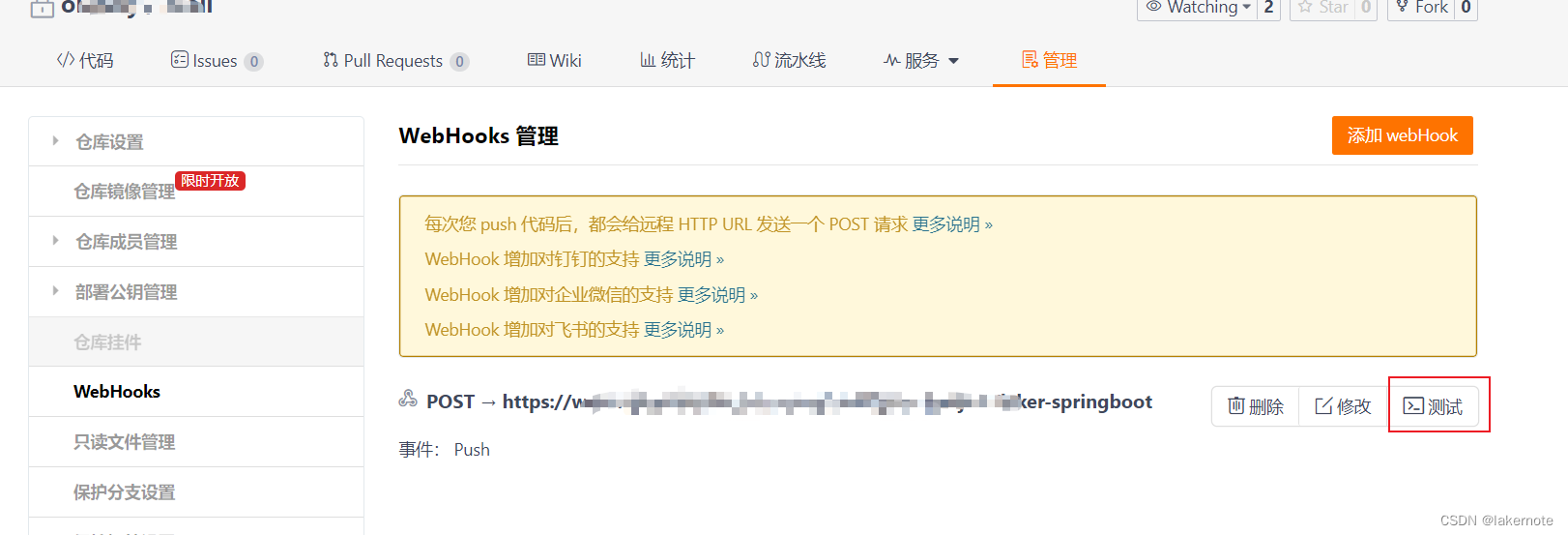
文章目录 安装安装JDK安装Maven安装GitNodeJS安装(可选)安装Jenkins 配置Jenkins为Jenkins更换插件源设置jenkins时区安装插件全局工具配置添加Gitee凭证Gitee项目配置 部署后端1.新建任务2.配置源码管理3.构建触发器4.到Gitee中添加WebHook5.构建环境6.…...

延迟任务基于DeyalQueue
一,延迟任务应用场景? 一般用于处理订单,将redis中的数据延迟存入数据库,实现异步存储减少DB的压力 二, 延迟任务的实现方案有很多 DelayQueue Redisson MQ 时间轮 原理 JDK自带延迟队列,基于阻塞队列…...

Linux 查询端口被占用命令
Linux 查询端口被占用命令 1、lsof -i:端口号 用于查看某一端口的占用情况,比如查看8000端口使用情况,lsof -i:8000 lsof -i:8080:查看8080端口占用 lsof abc.txt:显示开启文件abc.txt的进程 lsof -c abc:显示abc进…...
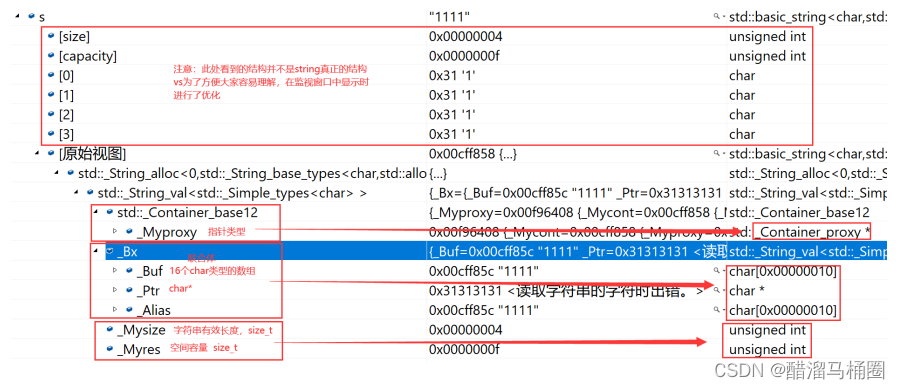
【c++】string类---标准库中的string类
1. 为什么要学习string类 1.1 C语言中的字符串 C语言中,字符串是以\0结尾的一些字符的集合,为了操作方便,C标准库中提供了一些str系列 库函数,但是这些库函数与字符串是分离开的,不太符合OOP的思想,而且…...
(五))
GO语言学习笔记(与Java的比较学习)(五)
Map 概念 map 是引用类型,可以使用如下声明: var map1 map[keytype]valuetype var map1 map[string]int 在声明的时候不需要知道 map 的长度,map 是可以动态增长的。 未初始化的 map 的值是 nil(即零值为nil)&…...
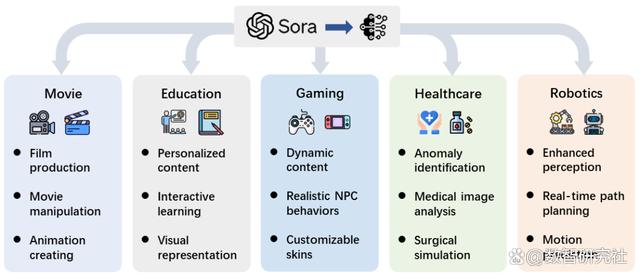
Sora:探索大型视觉模型的前世今生、技术内核及未来趋势
Sora,一款由OpenAI在2024年2月推出的创新性文生视频的生成式AI模型,能够依据文字说明,创作出既真实又富有想象力的场景视频,展现了其在模拟现实世界方面的巨大潜能。本文基于公开技术文档和逆向工程分析,全面审视了Sor…...
基于springboot实现图书馆管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现图书馆管理系统演示 摘要 电脑的出现是一个时代的进步,不仅仅帮助人们解决了一些数学上的难题,如今电脑的出现,更加方便了人们在工作和生活中对于一些事物的处理。应用的越来越广泛,通过互联网我们可以更方便地…...

MATLAB环境下基于高斯滤波器-广义拉普拉斯算子的细胞核自动检测
作为病理图像分析的基础,细胞核检测可为细胞形态、纹理等多种相关分析提供支持,对于临床诊断具有重要意义。但是细胞核的人工识别过程十分费时费力,并且不同医生之间存在主观标注差异。因此,利用计算机技术进行自动检测能够更为客…...

【探索AI】十一 深度学习之第1周:深度学习概述与基础
深度学习概述与基础 深度学习的发展历史与现状神经网络的基本原理前向传播与反向传播算法常见的激活函数与优化算法深度学习框架(如TensorFlow或PyTorch)进行基础操作 深度学习的发展历史与现状 深度学习的发展历史可以追溯到上世纪40年代,当…...

【简说八股】Spring事务失效可能是哪些原因?
Spring事务介绍 Spring事务是指在Spring框架中对数据库操作进行管理的一种机制,它确保一组数据库操作要么完全执行成功(提交),要么完全不执行(回滚),从而保持数据一致性和完整性。 Spring框架…...

【语音识别】- CTC损失计算的原理
文章目录 1.符号定义与目标函数2.前向计算 α s ( t ) \alpha_s(t) α...

MySQL字符集和比较规则
MySQL字符集和比较规则 字符集和比较规则简介 字符集: 描述字符与二进制数据的映射关系 比较规则:比较指定字符集中的字符的规则 字符集 我们知道,计算机无法直接存储字符串,实际存储的都是二进制数据。字符集是有限的ÿ…...
)
备忘录模式(Memento Pattern)
定义 备忘录模式(Memento Pattern)是一种行为设计模式,它允许在不破坏封装性的前提下捕获一个对象的内部状态,并在以后将对象恢复到该状态。备忘录模式通常用于实现撤销操作(Undo)或历史记录(H…...

LeetCode 刷题 [C++] 第121题.买卖股票的最佳时机
题目描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的…...
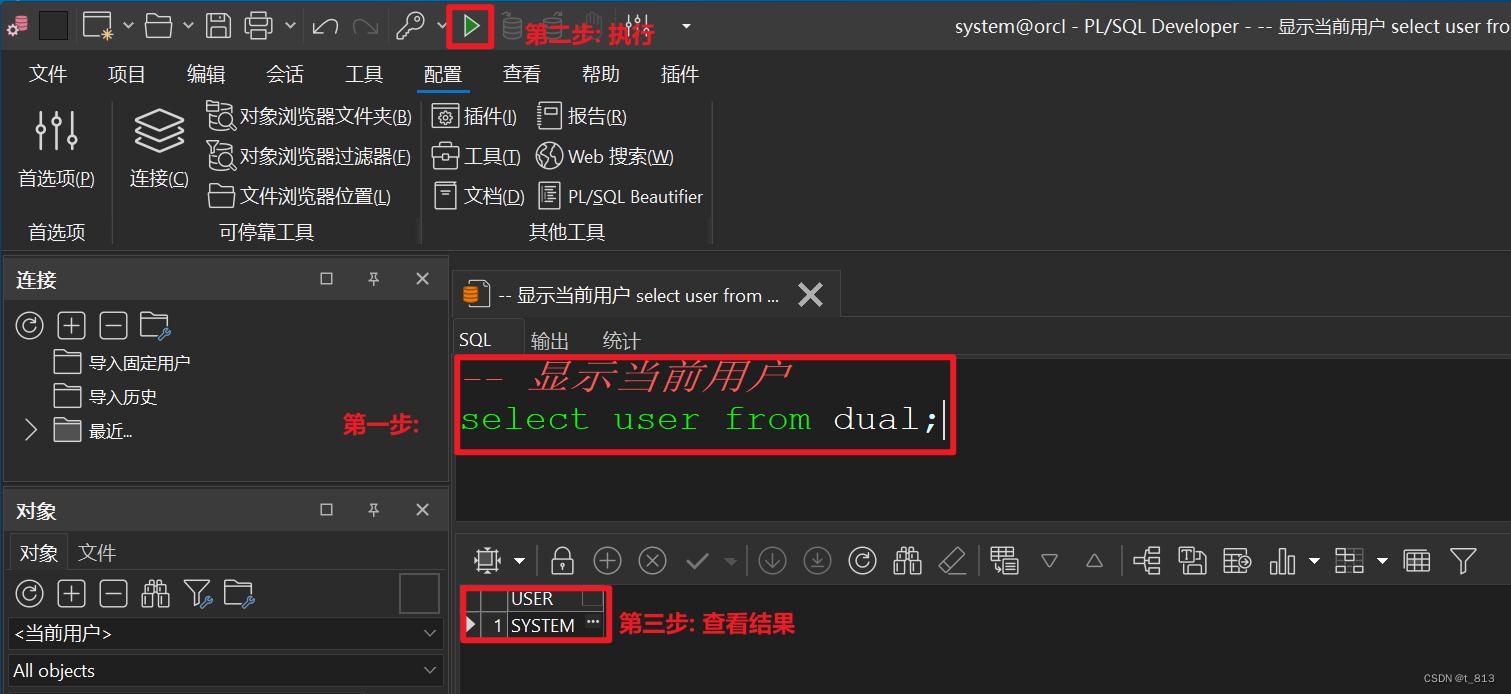
ORACLE 基础
一.ORACLE简介 1.1什么是oracle ORACLE 数据库系统是美国 ORACLE 公司(甲骨文)提供的以分布式数据库为核心的一组软件产品,是目前最流行的客户/服务器(CLIENT/SERVER)或 B/S 体系结构的数据库之一。 ORACLE 通常应用于大型系统的数据库产品。…...
Adobe illustrator CEP插件调试
1.创建插件CEP面板,可以参考:http://blog.nullice.com/%E6%8A%80%E6%9C%AF/CEP-%E5%BC%80%E5%8F%91%E6%95%99%E7%A8%8B/%E6%8A%80%E6%9C%AF-CEP-%E5%BC%80%E5%8F%91%E6%95%99%E7%A8%8B-Adobe-CEP-%E6%89%A9%E5%B1%95%E5%BC%80%E5%8F%91%E6%95%99%E7%A8%8…...

学会玩游戏,智能究竟从何而来?
最近在读梅拉妮米歇尔《AI 3.0》第三部分第九章,谈到学会玩游戏,智能究竟从何而来? 作者: [美] 梅拉妮米歇尔 出版社: 四川科学技术出版社湛庐 原作名: Artificial Intelligence: A Guide for Thinking Humans 译者: 王飞跃 / 李玉珂 / 王晓…...
Unity 常用操作
2D素材网站 https://craftpix.net/ https://itch.io/game-assets/tag-2d/tag-backgrounds 3D素材资源网址 https://www.mixamo.com/#/ 场景常用操作: 快捷键:QWER Q:Q键或鼠标中键,可以拉动场景。 W:选中物体后&…...
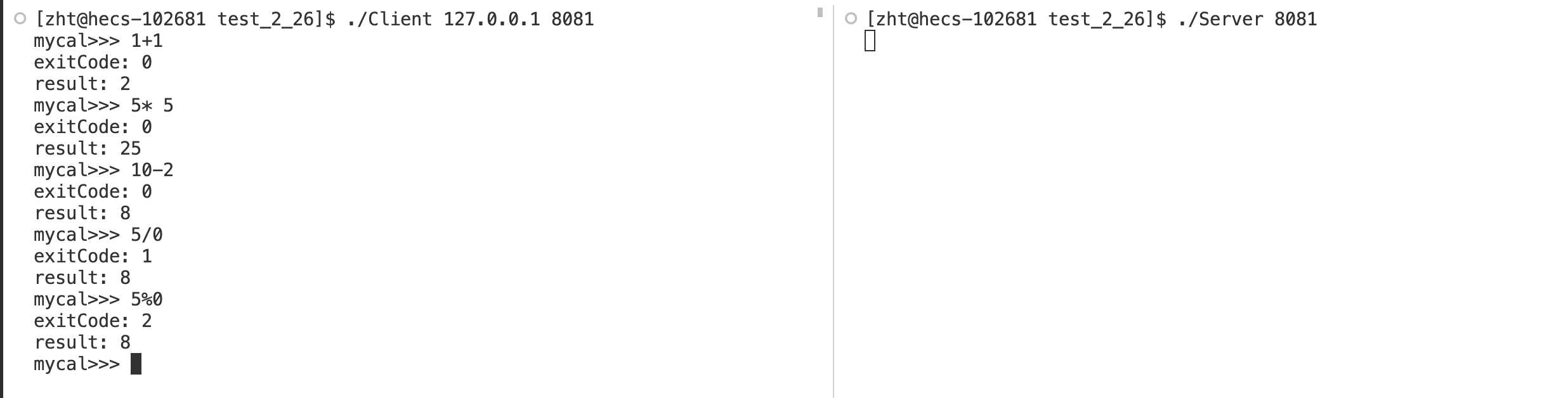
【计算机网络_应用层】协议定制序列化反序列化
文章目录 1. TCP协议的通信流程2. 应用层协议定制3. 通过“网络计算器”的实现来实现应用层协议定制和序列化3.1 protocol3.2 序列化和反序列化3.2.1 手写序列化和反序列化3.2.2 使用Json库 3.3 数据包读取3.4 服务端设计3.5 最后的源代码和运行结果 1. TCP协议的通信流程 在之…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
