搜索回溯算法(DFS)1------递归
目录
简介:
递归问题解题的思路模板
例题1:汉诺塔
例题2:合并两个有序链表
例题3:反转链表
例题4:两两交换链表中的节点
例题5:Pow(x,n)-快速幂
结语:
简介:
本系列将会带大家深入理解搜索中的一大分支深搜,深搜是离不开递归的和回溯思想的(优化需要剪枝),故我会在例题中详细指出解决这一系列问题的思考思路和解题技巧。
那么我们就从递归开始(深搜的基础)也就是本文中主要介绍的。
什么是递归?
简单来说就是函数自己调用自己。
为什么会用到递归?
大问题可以拆解成相同的子问题,且子问题的解法和大问题的一模一样,这是就可以用到递归。

在解决⼀个规模为n的问题时,如果满⾜以下条件,我们可以使用递归来解决:
a. 问题可以被划分为规模更⼩的⼦问题,并且这些⼦问题具有与原问题相同的解决⽅法。
b. 当我们知道规模更⼩的⼦问题(规模为n-1)的解时,我们可以直接计算出规模为n的问题的解。
c. 存在⼀种简单情况,或者说当问题的规模⾜够⼩时,我们可以直接求解问题。
⼀般的递归求解过程如下:
a. 验证是否满⾜简单情况。
b. 假设较⼩规模的问题已经解决,解决当前问题。
上述步骤可以通过数学归纳法来证明。
如何理解递归?
不要太在意细节,相信函数。
递归问题解题的思路模板
当然在设计递归函数之前最重要的是你要你的递归函数干嘛。
1.递归函数的作用
2.相同子问题------------函数头
3.只关心某一个子问题是如何解决的------------函数体
4.递归出口
建议友友在写递归类型的题目是一定要把这三个地方考虑清楚了再下手。
最后就是相信函数。
例题1:汉诺塔
链接:汉诺塔
题目简介:
递归问题非常经典的一道题目,在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。

解法:
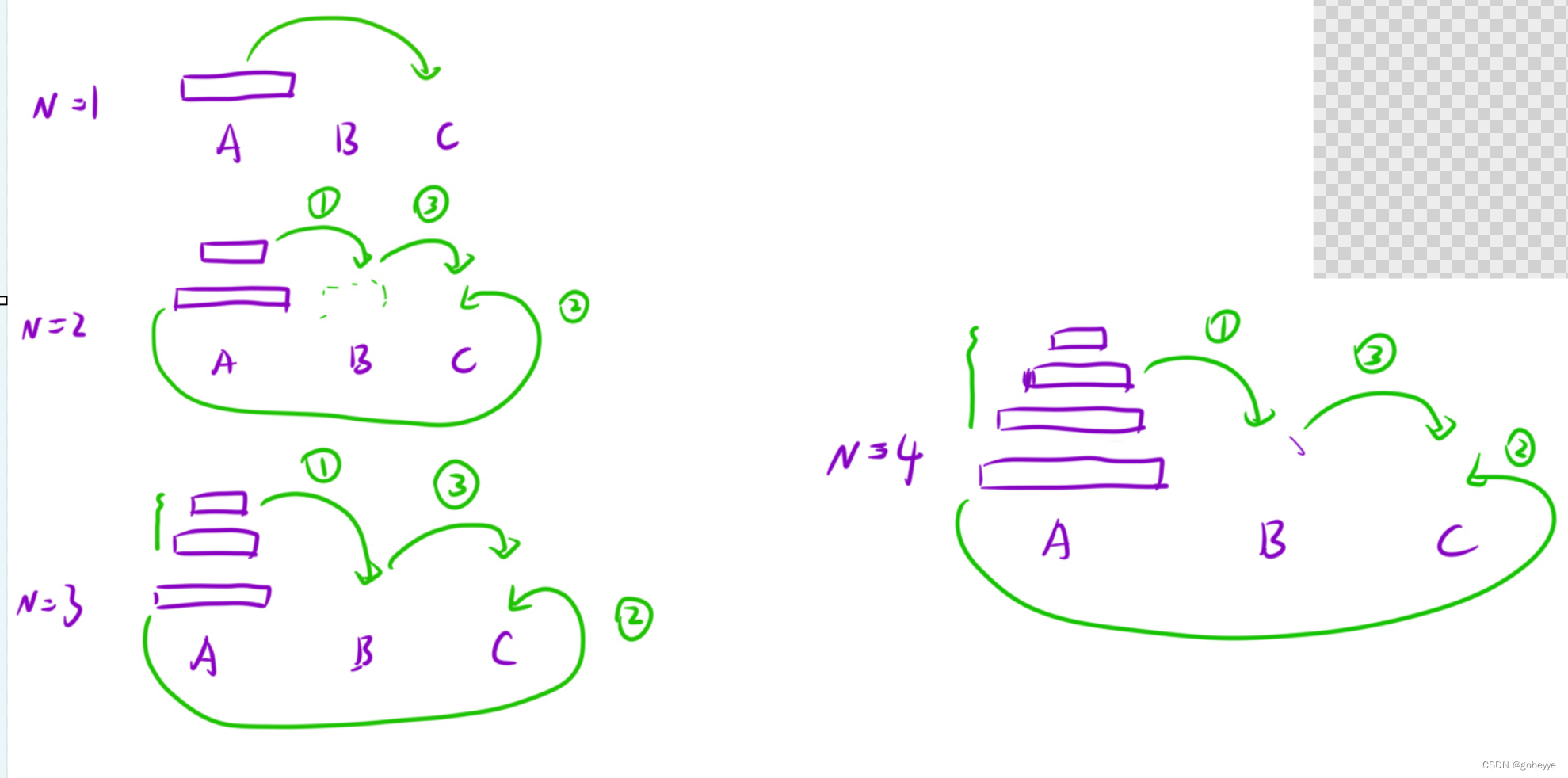
我们可以看到每次都可以把大问题分解成相同的子问题,且子问题的解决方法和大问题的一模一样故我们可以使用递归来处理。
1.递归函数的作用
函数作⽤:将A中的上⾯n个盘⼦挪到C中。这里的A和C是函数参数的A和C不是实际的(很重要)。
2.相同子问题(函数头)
我们要设计一个函数头来完成汉诺塔的递归过程,我们可以看到我们需要三根柱子和要记录下来还剩下几个盘子。故我们的函数头可以设计成public void dfs(List<Integer> a, List<Integer> b, List<Integer> c, int n)。关于List<Integer>如果友友还没有学到的话可以把他看成一个数组。
3.只关心某一个子问题是如何解决的(函数体)
我们取第三层汉诺塔来研究(大问题被拆成3层汉诺塔)。
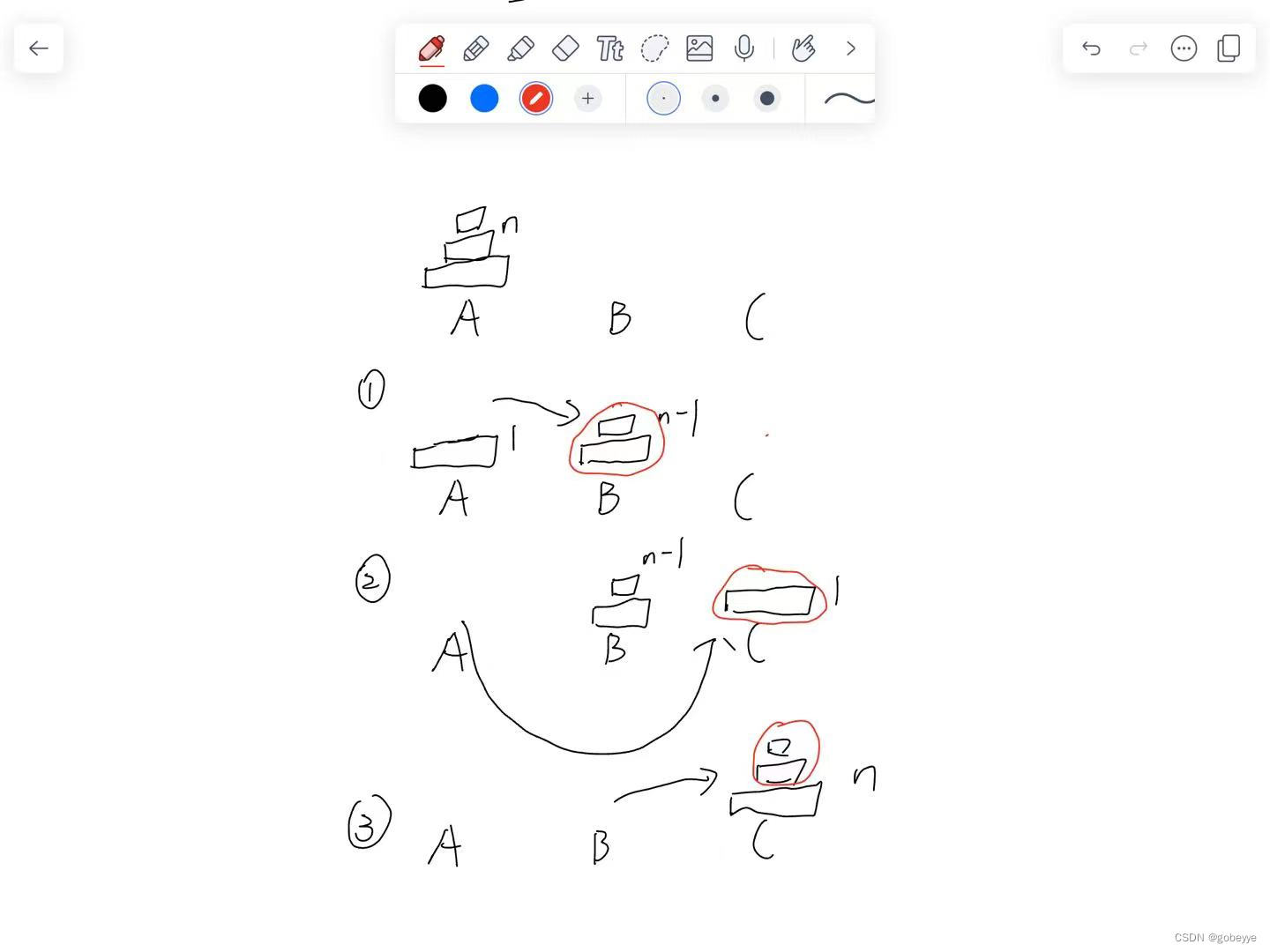
我们发现子问题刚来三件事
1.把A上面n - 1 个盘子通过C移动到B
2.把A上面最后一个盘中移动到C
3.把B上面n - 1个盘中通过A 移动到C
dfs(a, c, b, n - 1);
c.add(a.remove(a.size() - 1));//这里是因为给出的例题这样做就是把盘中从A移动到C(理解思路即可)
dfs(b, a, c, n - 1);
4.递归出口
当问题的规模变为n=1时,即只有⼀个盘⼦时,我们可以直接将其从A柱移动到C柱。
本例题代码实现如下:
class Solution {public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {dfs(A,B,C,A.size());}public void dfs(List<Integer> A, List<Integer> B, List<Integer> C,int n ){if(n == 1){C.add(A.remove(A.size() - 1));return;}dfs(A,C,B,n - 1);C.add(A.remove(A.size() - 1));dfs(B,A,C,n - 1);}
}关于本例题要注意的点:c.add(a.remove(a.size() - 1));可能有的友友会纠结为什么不是remove(0)呢,其实自己模拟一下即可,我们移走盘子是从最上面那个盘子开始移动的。
不用太深究函数的细节(陷入将无法自拔),如果是第一次的话可以去b站上看看递归的全过程细节(这里的不用深究是建立在已经对它的展开有一定理解了,第一次学汉诺塔的话我还是建议大家可以看看别人推的整个过程,理解更加深刻)。
例题2:合并两个有序链表
链接:合并两个有序链表
题目简介:
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
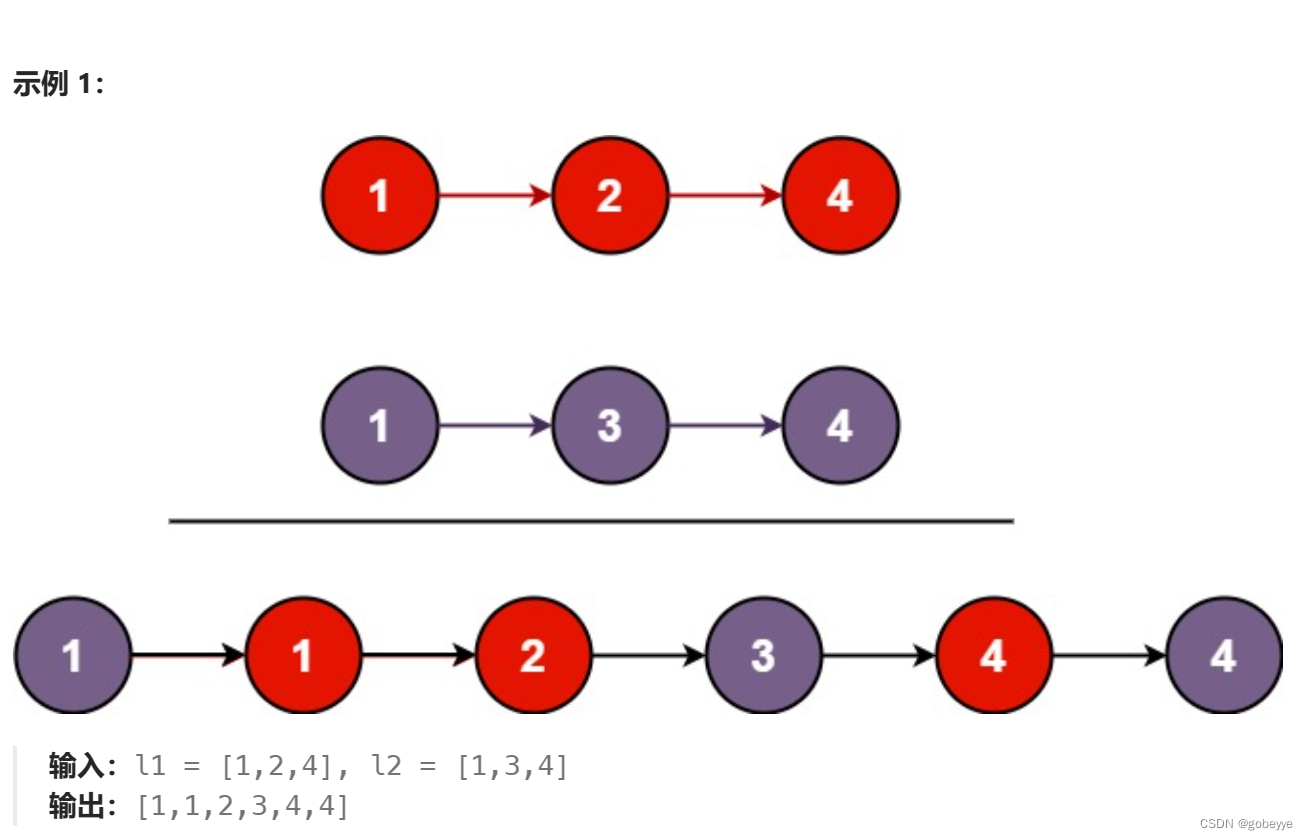
解法:
通过分析题目我们发现可以把大问题拆成下图的子问题,上面的1已经合并有序现在要让2,4和下面链表合并有序。
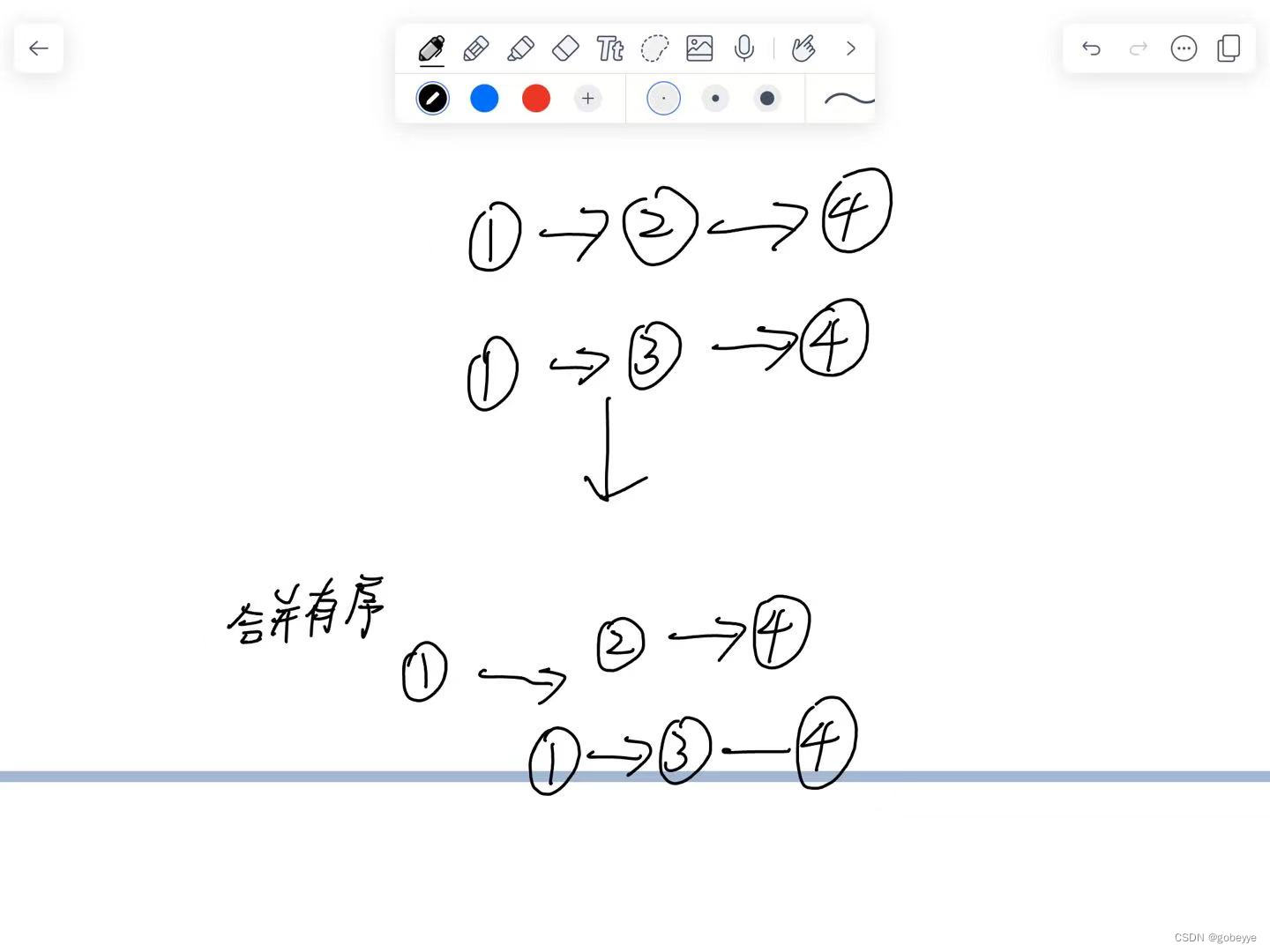
故我们可以用递归来解决这道问题。
1.递归函数的作用
交给你两个链表的头结点,你帮我把它们合并起来,并且返回合并后的头结点.
2.相同子问题(函数头)
由上图可以看到函数要包含两个链表还要能返回合并后的链表故函数头设定为:public ListNode mergeTwoLists(ListNode l1, ListNode l2)
3.只关心某一个子问题是如何解决的(函数体)
选择两个头结点中较小的结点作为最终合并后的头结点,然后将剩下的链表交给递归函数去处理。
4.递归出口
当某⼀个链表为空的时候,返回另外⼀个链表。
代码如下:
class Solution {public ListNode mergeTwoLists(ListNode list1, ListNode list2) {if(list1 == null){return list2;}if(list2 == null){return list1;}if(list1.val <= list2.val){list1.next = mergeTwoLists(list1.next,list2);return list1;}else{list2.next = mergeTwoLists(list1,list2.next);return list2;}}
}例题3:反转链表
链接:反转链表
题目简介:
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
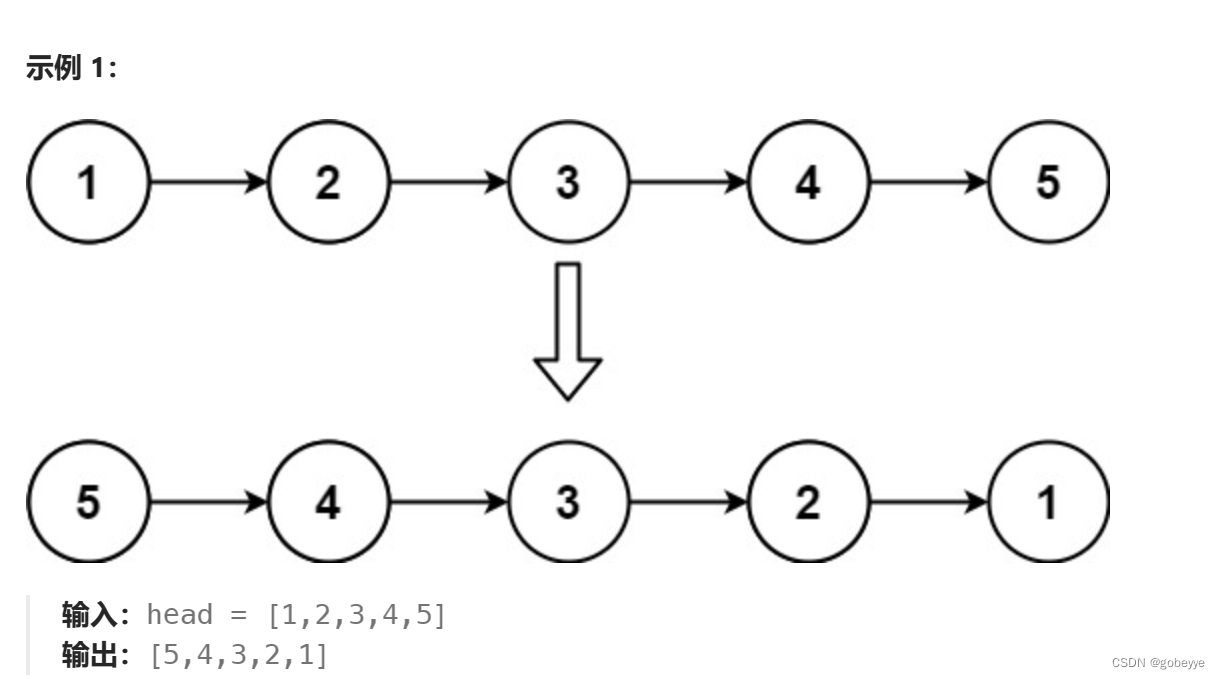
解法:
要想让1到5逆序,可以让5逆序后让1到4逆序一直这样下去我们不难发现这就是递归。
1.递归函数的作用
交给你⼀个链表的头指针,你帮我逆序之后,返回逆序后的头结点。
2.相同子问题(函数头)
需要传入链表,5节点逆序后要把逆序后的新头节点返回故将函数体设为public ListNode reverseList(ListNode head)
3.只关心某一个子问题是如何解决的(函数体)
先把当前结点之后的链表逆序,逆序完之后,把当前结点添加到逆序后的链表后⾯即可。
4.递归出口
当前结点为空或者当前只有⼀个结点的时候,不⽤逆序,直接返回。
代码如下:
class Solution {public ListNode reverseList(ListNode head) {ListNode newHead = head;if(head == null){return head;}ListNode cur = head.next;ListNode prev = head;head.next = null;while(cur != null){ListNode next = cur.next;cur.next = prev;prev = cur;cur = next;}return prev;}
}例题4:两两交换链表中的节点
链接:两两交换链表中的节点
题目简介:
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
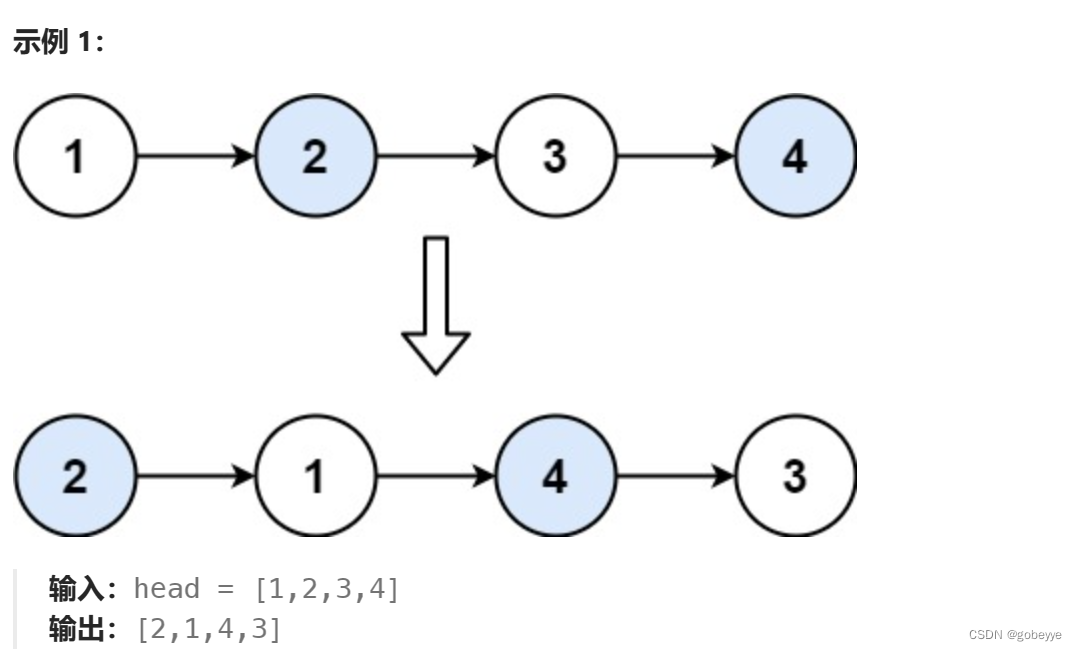
解法:
我们通过阅读题目可以发现要使整个链表两两交换 ,可以将大问题分为把1和2后面的节点两两交换,把一二交换即可,同理3和4也是同样的处理思路。
1.递归函数的作用
交给你⼀个链表,将这个链表两两交换⼀下,然后返回交换后的头结点;
2.相同子问题(函数头)
需要传入原始链表和返回新的头节点故设计为:public ListNode swapPairs(ListNode head)
3.只关心某一个子问题是如何解决的(函数体)
先去处理⼀下第⼆个结点往后的链表,然后再把当前的两个结点交换⼀下,连接上后面处理后的链表;
4.递归出口
当前结点为空或者当前只有⼀个结点的时候,不⽤交换,直接返回。
代码如下:
class Solution {public ListNode swapPairs(ListNode head) {if(head == null || head.next == null){return head;}ListNode newHead = head.next;head.next = swapPairs(head.next.next);newHead.next = head;return newHead;}
}例题5:Pow(x,n)-快速幂
链接:Pow(x,n)
题目简介:
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。

解法:
这题不能使用1个1个数的分离递归(会超时),我们这里要采用二分的思路,具体实现如下:
1.递归函数的作用
求出x 的n 次⽅是多少,然后返回;
2.相同子问题(函数头)
需要传入需要n次方的x和n还要将其返回public double pow(double x, int n)
3.只关心某一个子问题是如何解决的(函数体)
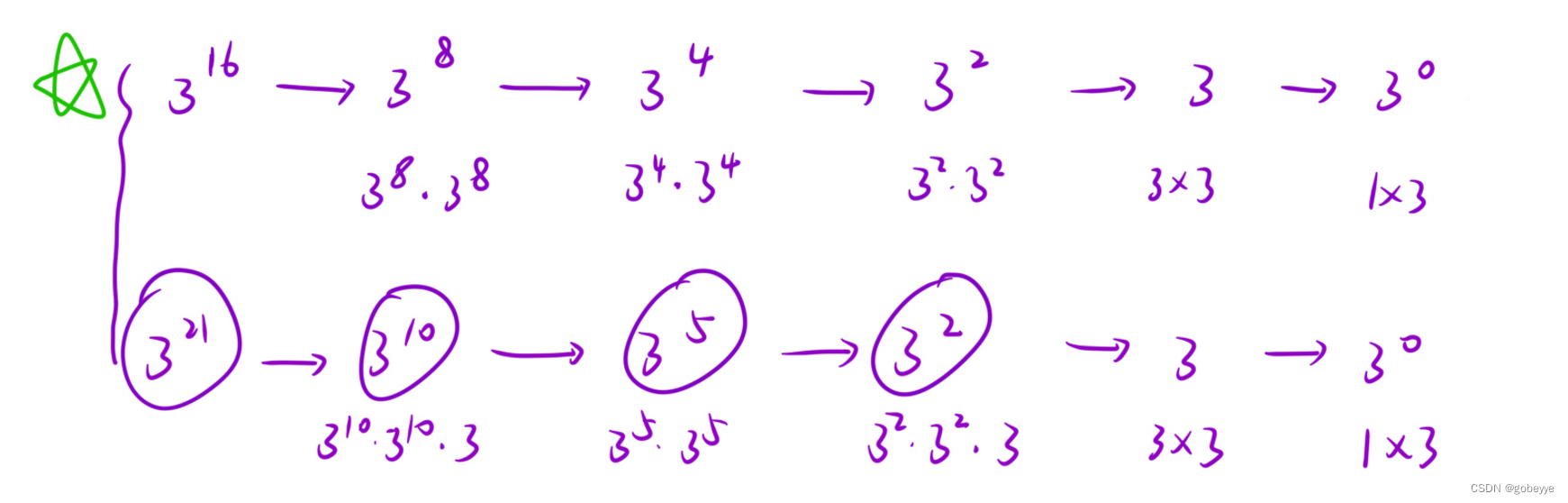
先求出x 的n / 2 次⽅是多少,然后根据n 的奇偶,得出x 的n 次⽅是多少;
4.递归出口
当n 为0 的时候,返回1 即可。
代码如下:
最上面要区分一下正负数的区别即可。
class Solution {public double myPow(double x, int n) {return (n < 0) ? 1.0 / pow(x, - n) : pow(x , n);}public double pow(double x,int n){if(n == 0){return 1.0;}double tmp = pow(x,n / 2);return (n % 2 == 0) ? tmp * tmp : tmp * tmp * x;}
}总结:本文章是搜索回溯的第一篇,带大家再复习了一下递归,后续的章节会带领大家深度理解深搜和回溯算法。
结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固自己的知识点,和一个学习的总结,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进,如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。
相关文章:
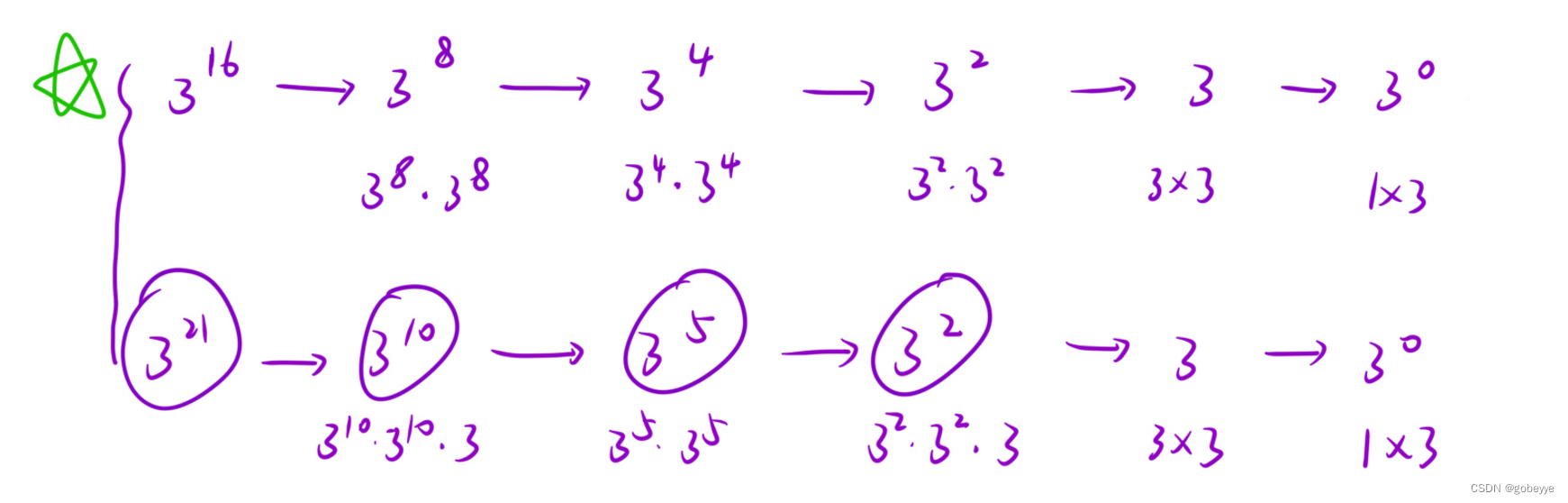
搜索回溯算法(DFS)1------递归
目录 简介: 递归问题解题的思路模板 例题1:汉诺塔 例题2:合并两个有序链表 例题3:反转链表 例题4:两两交换链表中的节点 例题5:Pow(x,n)-快速幂 结语: 简介&…...

workstation 用途
一 workstation 用途 强大的桌面虚拟化 允许创造多种操作系统可以不用重启就跨不同操作系统进行操作可以提供隔离的安全环境 连接到vsphere 可以远程登陆服务器管理物理主机和虚拟主机任何时间都可登陆提高虚拟机效率 为任何平台开发和测试 1)借助一台单一本地…...

【三维重建】【SLAM】SplaTAM:基于3D高斯的密集RGB-D SLAM(CVPR 2024)
题目:SplaTAM: Splat, Track & Map 3D Gaussians for Dense RGB-D SLAM 地址:spla-tam.github.io 机构:CMU(卡内基梅隆大学)、MIT(美国麻省理工) 总结:SplaTAM,一个新…...

Go Barrier栅栏
1. 简介 实现与pythonthreading.Barrier库类似的功能,多线程同时等待达到指定数量一起放行。 有待改进地方: wait方法没有支持context控制。 2. 代码 import ("context""golang.org/x/sync/semaphore""sync/atomic" …...

[蓝桥杯 2023 省 B] 冶炼金属
P9240 [蓝桥杯 2023 省 B] 冶炼金属 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 参考题解: #C3150——蓝桥杯2023年第十四届省赛真题-冶炼金属(分块)-Dotcpp编程社区 https://www.bilibili.com/video/BV1wc411x7KU/?spm_id_from333.1007.top_right_bar_windo…...

续Java的执行语句、方法--学习JavaEE的day07
day07 一、特殊的流程控制语句 break(day06) continue 1.理解: 作用于循环中,表示跳过循环体剩余的部分,进入到下一次循环 做实验: while(true){ System.out.println(“111”); System.out.println(“222”); if(true){ conti…...

公网IP怎么获取?
公网IP是网络中设备的唯一标识符,用于在Internet上进行通信和定位。对于普通用户来说,了解如何获取自己的公网IP是很有必要的,本文将介绍几种获取公网IP的方法。 方法一:通过路由器查询 大多数家庭和办公室使用的路由器都会有一个…...

连接未来:探索嵌入式系统的智能化之路
连接未来:探索嵌入式系统的智能化之路 嵌入式系统的智能化是连接未来的关键之一。以下是对这一主题的小点论述: 1. 嵌入式系统的定义和特点 嵌入式系统是一种特殊用途的计算机系统,通常嵌入在其他设备中,具有小巧、低功耗、实时…...
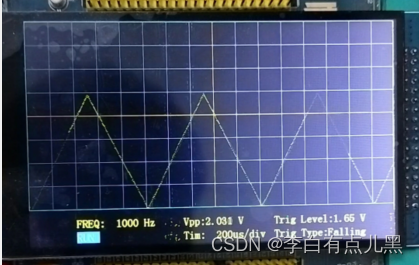
基于STM32制作的示波器(可对任意信号进行描点)
基于STM32制作的示波器(可对任意信号进行描点) 注意:用的屏幕是TFT-LCD(MCU 屏)正点原子同款屏幕 液晶显示器,即 Liquid Crystal Display,利用了液晶导电后透光性可变的特性,配合显…...

WEB APIs (5)
window对象 BOM(浏览器对象模型) 其为js操作浏览器提供了方法 window对象是一个全局变量,是BOM树根节点 BOM的属性和方法都是window的,如document、console.log()等 var定义在全局全局作用域中的变量、函数都会变成window对象…...

物联网常见协议篇
在物联网环境中,物联网协议承担着关键作用,而新手了解物联网协议如传输协议、通讯协议和行业协议等。 一、物联网协议 物联网协议是物联网环境中的关键组成部分,它承担着设备间通信和数据传输的重要任务。这些协议根据其作用的不同ÿ…...
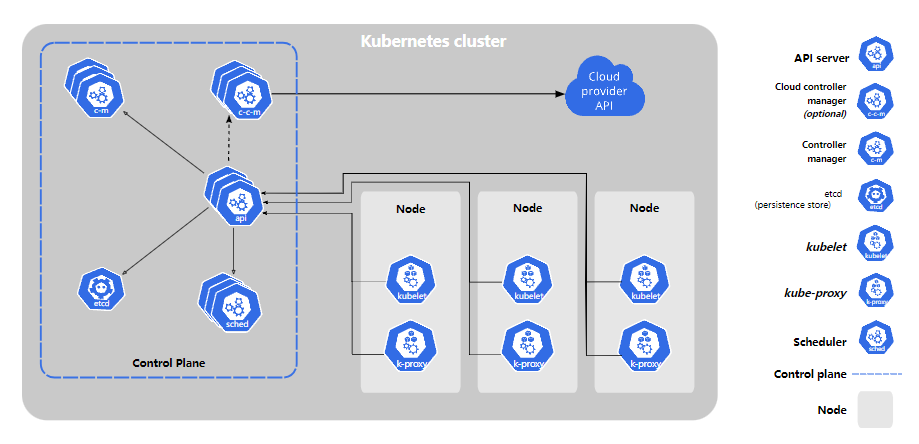
Kubernetes-1
学习Kubernetes第一天 k8s-11、什么是Kubernetes2、配置Kubernetes2.1、准备三台全新的虚拟机2.2、关闭防火墙和SElinux2.3、修改主机名2.4、升级操作系统(三台一起操作)2.5、配置主机hosts文件,相互之间通过主机名互相访问2.6、配置master和node之间的免密通道2.7、…...

SpringMVC框架②
三、RequestMapping注解 3、RequestMapping注解的value属性 必须设置 发送一个请求最直观的表示方式就是一个请求路径 altenter 进入接口方法 再用 alte7 查看里面的属性 value值可以是数组 value{"test","test1"} 只满足任何一个请求地址就会调用此方…...
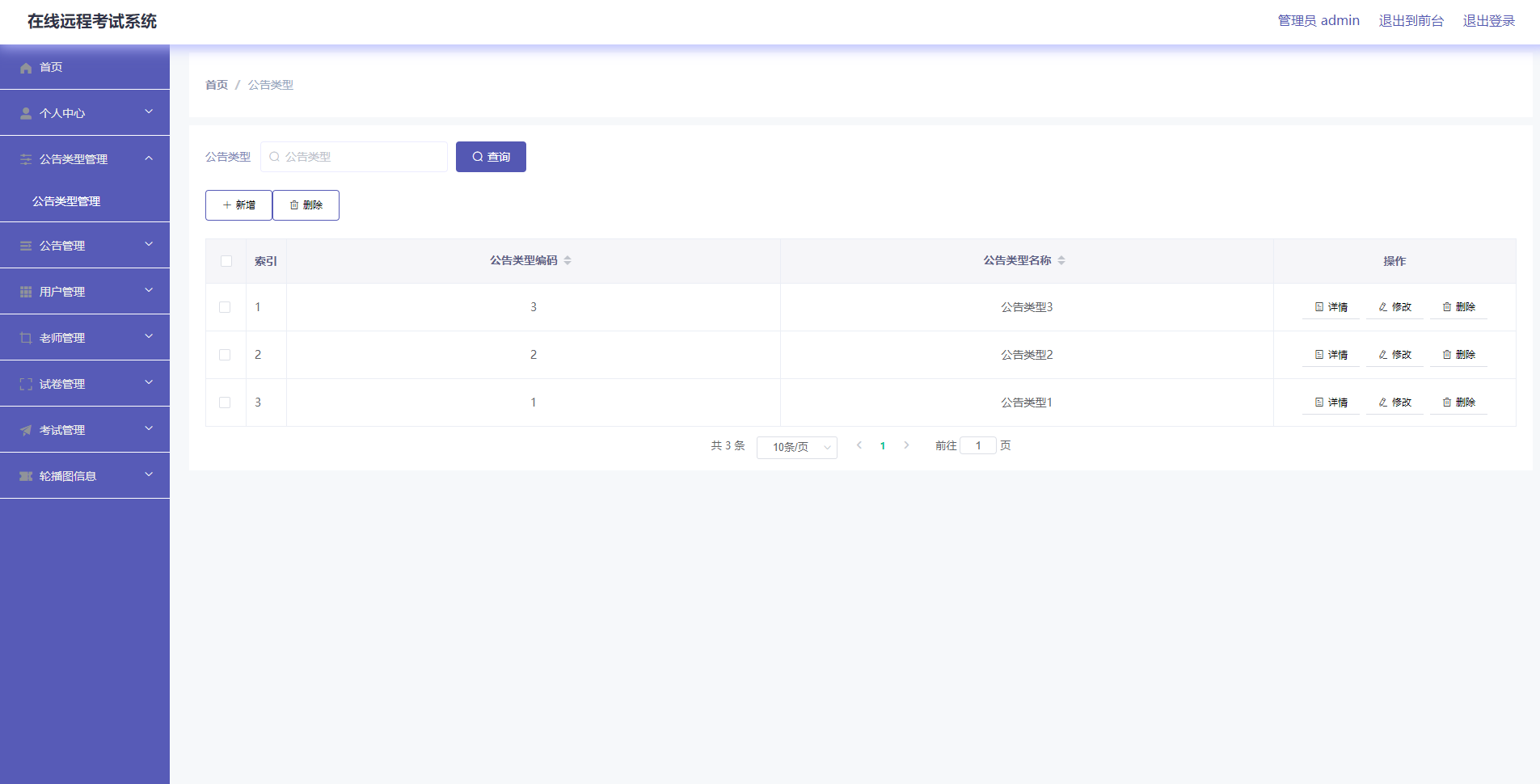
springboot230基于Spring Boot在线远程考试系统的设计与实现
在线远程考试系统设计与实现 摘 要 信息数据从传统到当代,是一直在变革当中,突如其来的互联网让传统的信息管理看到了革命性的曙光,因为传统信息管理从时效性,还是安全性,还是可操作性等各个方面来讲,遇到…...
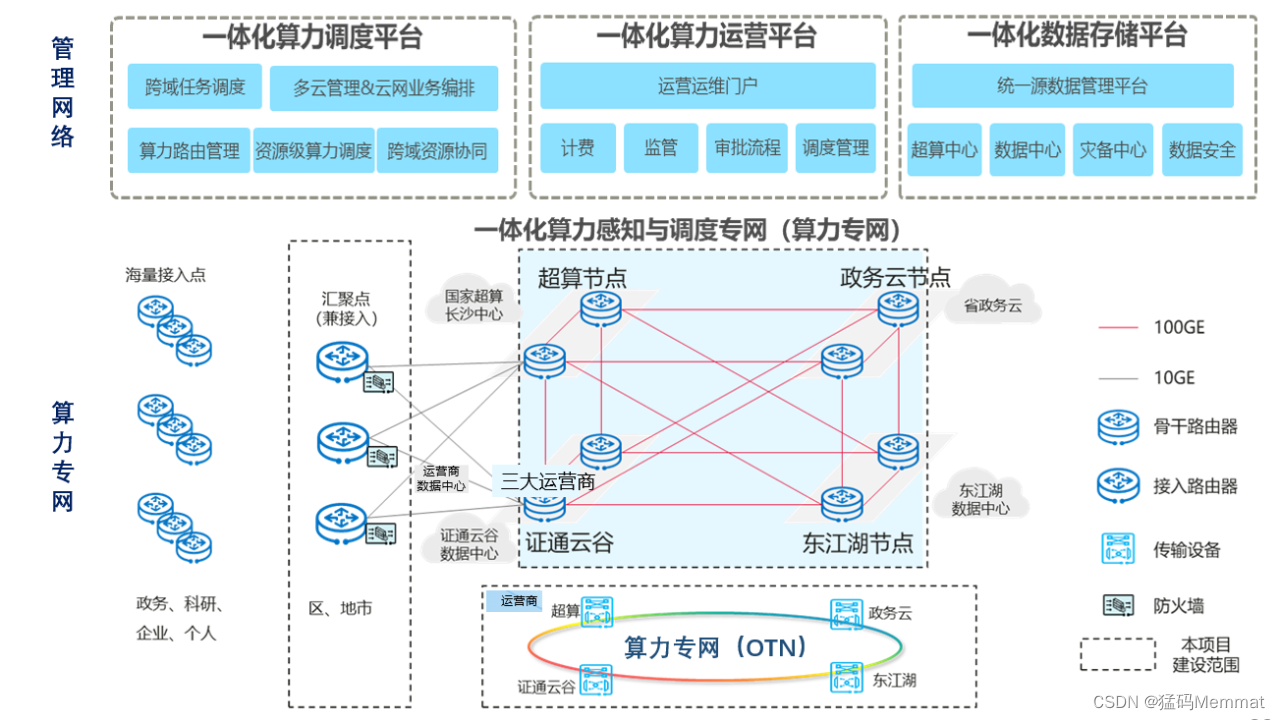
盘点:国家智能算力中心
文章目录 1. Main2. My thoughtsReference 1. Main 按照《中国算力白皮书(2022年)》的定义,算力主要分为四部分:通用算力、智能算力、超算算力、边缘算力。通用算力以CPU芯片输出的计算能力为主;智能算力以GPU、FPGA、…...

【C++】7-2 寻找完美数 分数 10
7-2 寻找完美数 分数 10 全屏浏览 切换布局 作者 李祥 单位 湖北经济学院 所有真因子之和小于其本身的数称为亏数。 如:4 的真因子 1、2 之和为 3,小于 4,是亏数。 所有真因子之和大于其本身的数称为盈数。 如:12 的真因子 1…...
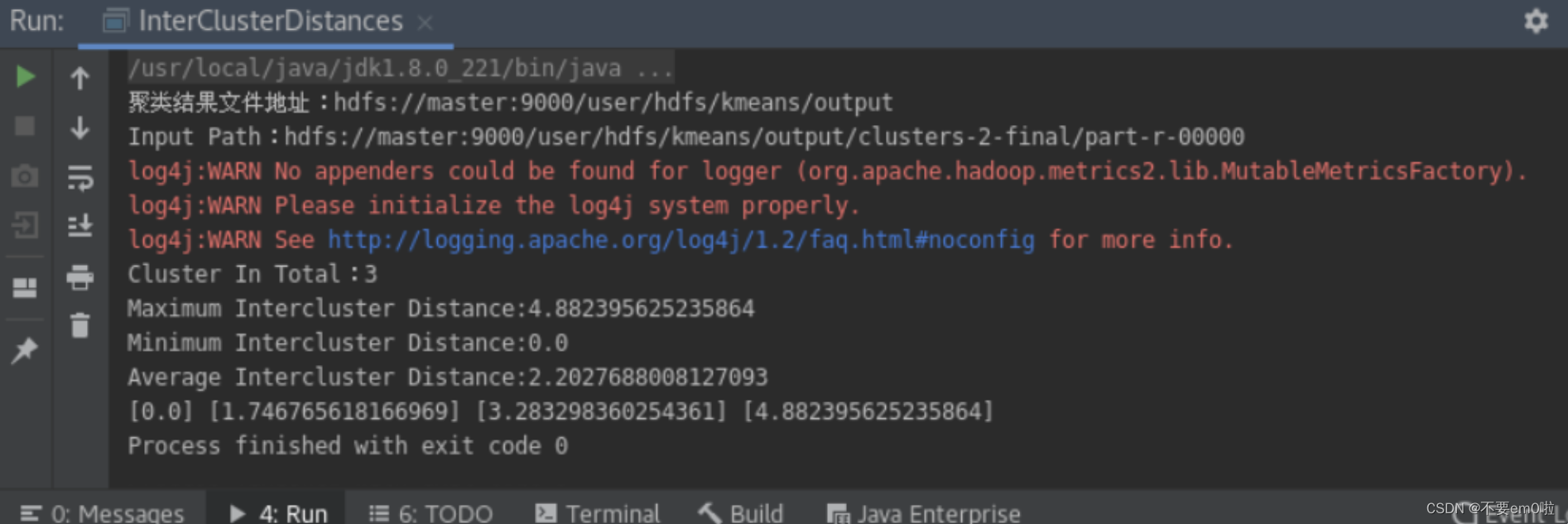
基于Mahout实现K-Means聚类
需求分析 需要对数据集进行预处理,选择合适的特征进行聚类分析,确定聚类的数量和初始中心点,调用Mahout提供的K-Means算法进行聚类计算,评估聚类结果的准确性和稳定性。同时,需要对Mahout的使用和参数调优进行深入学习…...
)
科技的成就(五十七)
535、Machine Learning "1959 年 7 月,塞缪尔首创 Machine Learning 一词。塞缪尔在“Some Studies in Machine Learning Using theGame of Checkers”一文中给 Machine Learning 下了个非正式定义:没有明确编程指令的情况下,能让计算机…...

动态IP代理技术在网络爬虫中的实际使用
目录 一、动态IP代理技术概述 二、动态IP代理技术的优势 三、动态IP代理技术的实际应用 四、注意事项 五、案例分析 六、结论 随着互联网的迅猛发展,网络爬虫成为了获取信息、分析数据的重要工具。然而,在进行大规模爬取时,爬虫常常面临…...

计算机网络:深入探索HTTP
引言: HTTP,全称超文本传输协议(Hypertext Transfer Protocol),是互联网上数据通信的基础。它定义了客户端(如浏览器)和服务器之间如何交互和传输数据。HTTP最初是为了支持Web浏览而设计的&…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
