求最短路径之迪杰斯特拉算法
对fill用法的介绍
1.用邻接矩阵实现
const int maxn=100;
const int INF=100000000;//无穷大,用来初始化边
int G[maxn][maxn];//用邻接矩阵存储图的信息
int isin[maxn]={false};//记录是否已被访问
int minDis[maxn];//记录到顶点的最小距离void Dijkstra(int s,int num){fill(minDis,minDis+num,INF);//先无穷大覆盖minminDis[s]=0;//令起始结点为0for(int i=0;i<num;i++){//记录最短距离及其对应下标:先初始化为最小int m=INF,centra=-1;for(int j=0;j<num;j++){//若未被访问且到顶点的最短距离最小if(isin[j]==false&&minDis[j]<m){//更新最短距离及其下标m=minDis[j];centra=j;}}//找不到最小的顶点了,说明此时剩余结点与顶点连通,无关INF,说明已结束if(centra==-1) return;isin[centra]=true;//开放与centra有关的顶点,并更新其当前到顶点的最小距离for(int k=0;k<num;k++){if(isin[k]==false&&G[centra][k]!=INF&&G[centra][k]+minDis[centra]<minDis[k])minDis[k]=G[centra][k]+minDis[centra];}}
}
记录最短路径
添加一个记录结点的数组即可,将它记录最短路径的结点的前一个结点
const int maxn=100;
const int INF=100000000;//无穷大,用来初始化边
int G[maxn][maxn];//用邻接矩阵存储图的信息
int isin[maxn]={false};//记录是否已被访问
int minDis[maxn];//记录到顶点的最小距离
int pre[maxn];//记录最短路径void Dijkstra(int s,int num){fill(minDis,minDis+num,INF);//先无穷大覆盖minminDis[s]=0;//令起始结点为0for(int i=0;i<num;i++)pre[i]=i;//初始化为自身for(int i=0;i<num;i++){//记录最短距离及其对应下标:先初始化为最小int m=INF,centra=-1;for(int j=0;j<num;j++){//若未被访问且到顶点的最短距离最小if(isin[j]==false&&minDis[j]<m){//更新最短距离及其下标m=minDis[j];centra=j;}}//找不到最小的顶点了,说明此时剩余结点与顶点连通,无关INF,说明已结束if(centra==-1) return;isin[centra]=true;//开放与centra有关的顶点,并更新其当前到顶点的最小距离for(int k=0;k<num;k++){if(isin[k]==false&&G[centra][k]!=INF&&G[centra][k]+minDis[centra]<minDis[k]){minDis[k]=G[centra][k]+minDis[centra];//记录最短距离pre[k]=u;//记录最短路径的前驱结点}}
}
void minPath(int begin,int now){//输出if(now==begin)//回溯到起点{cout<<begin;return;//跳到下一层}minPath(begin,pre[now]);cout<<now;//从起点后不断往外,输出结点}
2.用邻接表实现
#include <vector>
using namespace std;
const int maxn=100;
const int INF=10000000000;
bool isin[maxn]={false};
int path[maxn];
struct node{int id;//结点编号int value;//结点的边权
}nodes;
vector<node> v[maxn];void Dijisktra(int s,int num){int m,mp;fill(path,path+num,INF);path[s]=0;for(int i=0;i<num;i++){mp=INF;m=-1;for(int j=0;j<num;j++){if(isin[j]==false&&path[j]<mp){m=j;mp=path[j];}}if(m==-1) return;isin[m]=true;//只有这里与邻接矩阵不同,因为邻接表存储结点信息的方式不同 for(int k=0;k<num;k++){//v[m][k]-指的是顶点m中第k+1个与m相连的结点int index=v[m][k].id;if(isin[index]==false&&v[m][k].value+mp<path[index])path[index]=v[m][k].value+mp;}}
}
模拟简单实现
#include <iostream>
using namespace std;
const int maxn=100;
const int INF=10000000;
bool isin[maxn]={false};
int G[maxn][maxn],num,edge,begins;
int path[maxn];void Dijisktra(int s){fill(path,path+num,INF);path[s]=0;for(int i=0;i<num;i++){int m=-1,n=INF;for(int j=0;j<num;j++){if(isin[j]==false&&path[j]<n){m=j;n=path[j];}}if(m==-1) return;isin[m]=true;for(int k=0;k<num;k++){if(isin[k]==false&&G[m][k]!=INF&&G[m][k]+path[m]<path[k])path[k]=G[m][k]+path[m];}}
}
int main(){int v1,v2,weight;cin>>num>>edge>>begins;fill(G[0],G[0]+maxn*maxn,INF);//初始为无穷for(int i=0;i<edge;i++){cin>>v1>>v2>>weight;G[v1][v2]=weight;}Dijisktra(begins);for(int i=0;i<num;i++)if(i!=num-1)cout<<path[i]<<" ";else cout<<path[i]<<endl;return 0;
}
相关文章:

求最短路径之迪杰斯特拉算法
对fill用法的介绍 1.用邻接矩阵实现 const int maxn100; const int INF100000000;//无穷大,用来初始化边 int G[maxn][maxn];//用邻接矩阵存储图的信息 int isin[maxn]{false};//记录是否已被访问 int minDis[maxn];//记录到顶点的最小距离void Dijkstra(int s,in…...

python大学社团管理系统开发文档
项目介绍 一直想做一款大学社团管理系统,看了很多优秀的开源项目但是发现没有合适的。于是利用空闲休息时间开始自己写了一套管理系统。 在线体验 代码下载:https://github.com/geeeeeeeek/python_team演示地址:http://team.gitapp.cn/ &…...

leetcode 1328.破坏回文串
题目链接LeetCode1328 1.题目 给你一个由小写英文字母组成的回文字符串 palindrome ,请你将其中 一个 字符用任意小写英文字母替换,使得结果字符串的 字典序最小 ,且 不是 回文串。 请你返回结果字符串。如果无法做到,则返回一个…...
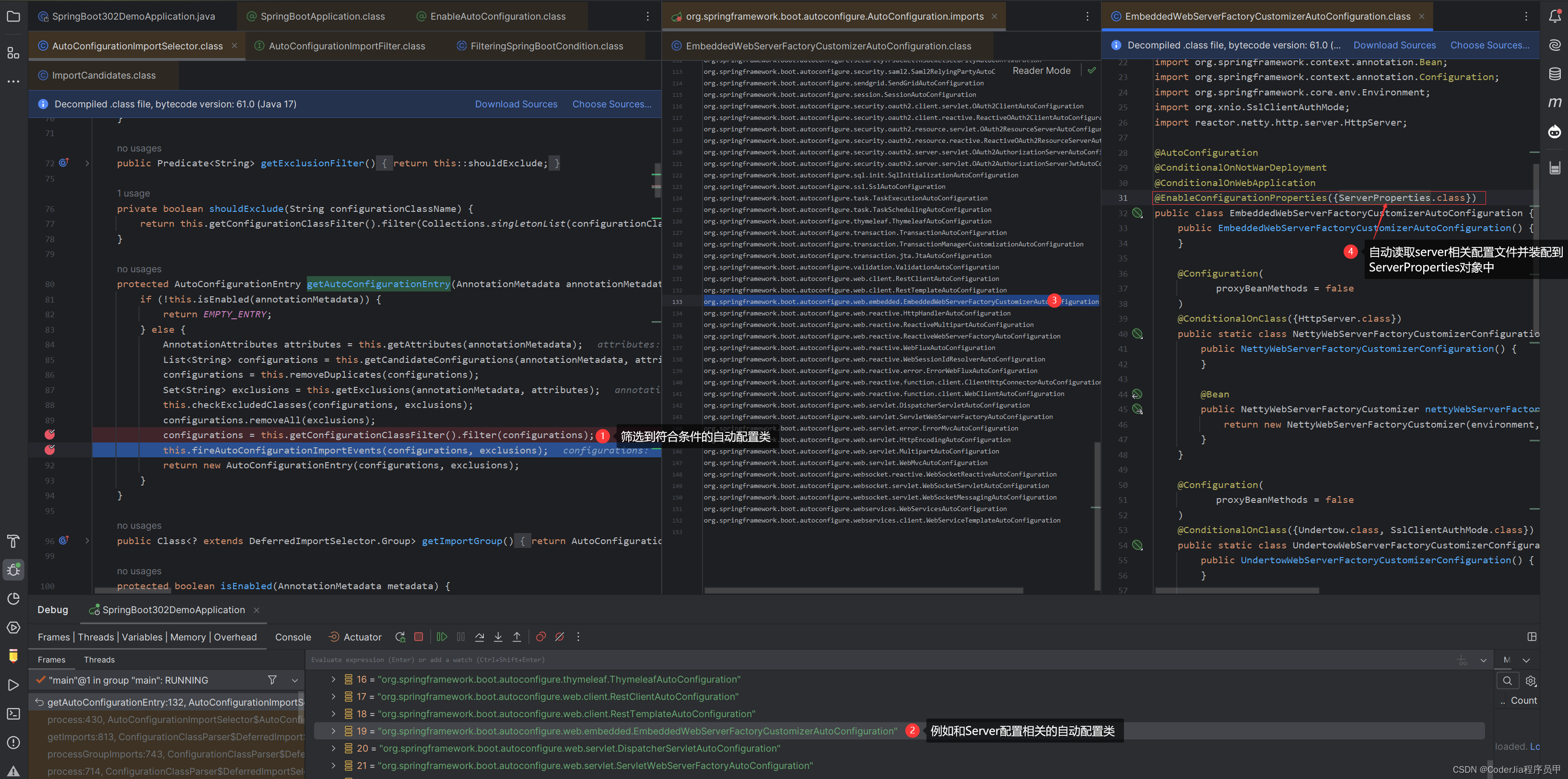
重学SpringBoot3-自动配置机制
重学SpringBoot3-自动配置机制 引言Spring Boot 自动配置原理示例:Spring Boot Web 自动配置深入理解总结相关阅读 引言 Spring Boot 的自动配置是其最强大的特性之一,它允许开发者通过最少的配置实现应用程序的快速开发和部署。这一切都得益于 Spring …...
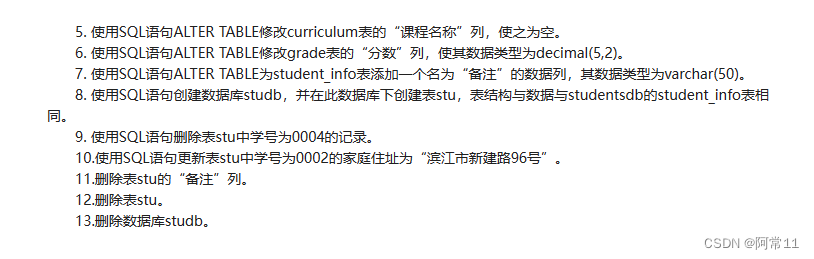
sql基本语法+实验实践
sql语法 注释: 单行 --注释内容# 注释内容多行 /* 注释内容 */数据定义语言DDL 查询所有数据库 show databases;注意是databases而不是database。 查询当前数据库 select database();创建数据库 create database [if not exists] 数据库名 [default charset 字符…...

Node.js中的并发和多线程处理
在Node.js中,处理并发和多线程是一个非常重要的话题。由于Node.js是单线程的,这意味着它在任何给定时间内只能执行一个任务。然而,Node.js的事件驱动和非阻塞I/O模型使得处理并发和多线程变得更加高效和简单。在本文中,我们将探讨…...

node.js 封装分页查询
node.js封装sql分页查询 方法: /*** 生成分页查询sql* param {string} table 表名* param {number} pageNum 分页页数 * param {number} pageSize 分页条数 * param {object} query 查询对象 例:{id:1,name:小明}* returns sql语句*/ const limit (ta…...

iptables 基本使用
iptables 主要用到两个表:filter 和 nat,其中 filter 表可以用来过滤数据包;nat 可以用来修改数据包的源地址和目的地址。 chain chain 是 table 中对数据包进行匹配的规则,对于 filter 来说 chain 有 INPUT & OUTPUT & …...
)
食品笔记()
吃东西有时不注意,就容易不舒服,记录下。 辣椒 辣椒真是个让人又爱又恨的东西。 看着想吃,吃着过瘾,吃完容易肚子疼。 主要是这东西本身就会刺激身体,即使是能吃辣的人,也容易造成肠胃发炎。 适量吃些即…...

C++入门和基础
目录 文章目录 前言 一、C关键字 二、命名空间 2.1 命名空间的定义 2.2 命名空间的使用 2.3 标准命名空间 三、C输入&输出 四、缺省参数 4.1 缺省参数的概念 4.2 缺省参数的分类 五、函数重载 5.1 函数重载的简介 5.2 函数重载的分类 六、引用 6.1 引用的…...
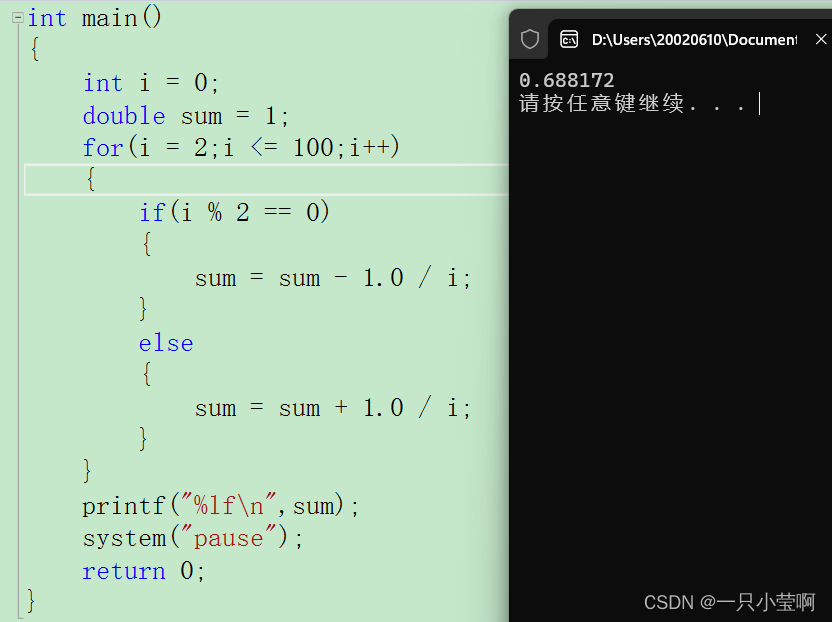
一些C语言知识
C语言的内置类型: char short int long float double C99中引入了bool类型,用来表示真假的变量类型,包含true,false。 这个代码的执行结果是什么?好好想想哦,坑挺多的。 #include <stdio.h>int mai…...
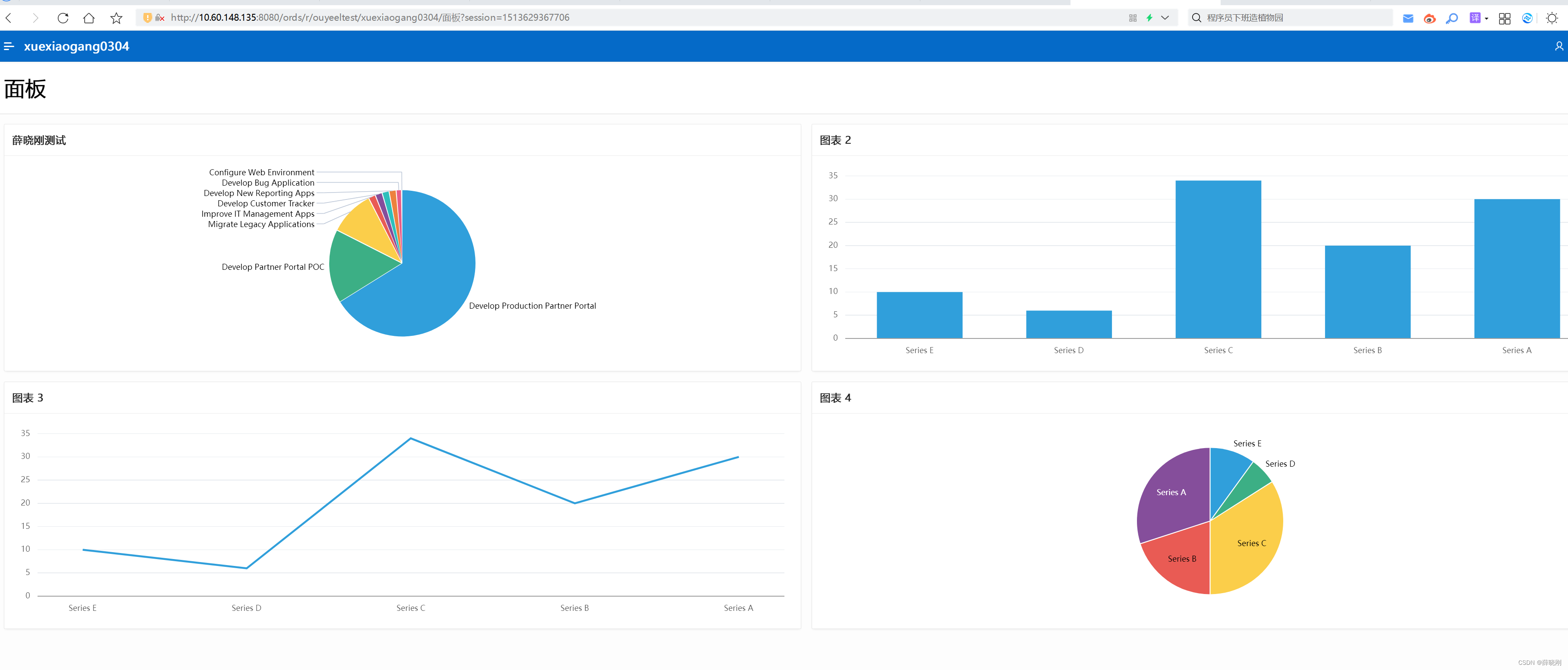
代码工具APEX的入门使用(未包含安装)
第一次使用APEX是2019年,这个技术成名已久只是我了解的比较晚。请看Oracle ACE的网站,这就是用APEX做的。实际上有一次我看O记的人操作他们的办公流程,都是用APEX做的。 那一年,我用APEX做了一个CMDB的管理系统。那时候还没有流行…...
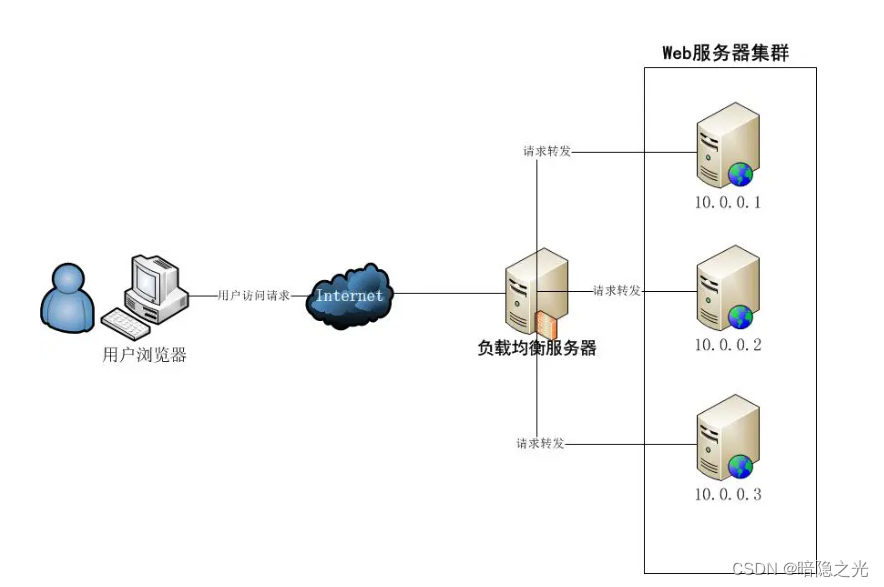
负载均衡.
简介: 将请求/数据【均匀】分摊到多个操作单元上执行,负载均衡的关键在于【均匀】。 负载均衡的分类: 网络通信分类 四层负载均衡:基于 IP 地址和端口进行请求的转发。七层负载均衡:根据访问用户的 HTTP 请求头、URL 信息将请求转发到特定的主机。 载体维度分类 硬…...

Git 指令深入浅出【2】—— 分支管理
Git 指令深入浅出【2】—— 分支管理 分支管理1. 常用分支管理指令2. 合并分支合并冲突合并模式 3. 实战演习 分支管理 1. 常用分支管理指令 # 查看本地分支 git branch# 查看远程分支 git branch -r# 查看全部分支 git branch -aHEAD 指向的才是当前的工作分支 # 查看当前分…...

工作流/任务卸载相关开源论文分享
decima-sim 概述: 图神经网络强化学习处理多工作流 用的spark的仿真环境,mit的论文,价值很高,高被引:663仓库地址:https://github.com/hongzimao/decima-sim论文:https://web.mit.edu/decima/co…...

为什么要用Python?
为什么要用Python? Python简单易用:提供大量的简单易用数据结构和内置库,语法结构也很简单易读,不需要使用括号来进行代码块分组,也不需要预声明变量或参数。Python开发效率高:简单易用的前提下࿰…...

北京大学发布,将试错引入大模型代理学习!
引言:探索语言智能的新边界 在人工智能的发展历程中,语言智能始终是一个核心的研究领域。随着大语言模型(LLM)的兴起,我们对语言智能的理解和应用已经迈入了一个新的阶段。这些模型不仅能够理解和生成自然语言&#x…...

Java 设计模式
编程设计模式六大原则 开闭原则(Open Close Principle):对扩展开放,对修改关闭。在程序需要进行拓展的时候,不能去修改原有的代码,实现一个热插拔的效果。简言之,是为了使程序的扩展性好&#…...

Kivy和BeeWare 开发APP的优缺点,及其发展历史
Kivy和BeeWare都是流行的Python框架,用于开发移动应用。它们各自有独特的特点和优势,同时也面临一些挑战和限制。下面是对这两个框架的开发优缺点及其发展历史的总结。 Kivy 发展历史 起源:Kivy诞生于2010年,旨在提供一个用于P…...

C++递推
统计每个月兔子的总数 #include<bits/stdc.h> using namespace std; int n,sum0; void f(int); int main() {int a[1000];cin>>n;a[1]1;a[2]2;for(int i3;i<1000;i){a[i]a[i-1]a[i-2];}cout<<a[n];return 0; } void f(int n){}猴子吃桃子 #include<b…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
