特征值和特征向量及其在机器学习中的应用
特征值和特征向量是线性代数中的概念,用于分析和理解线性变换,特别是由方阵表示的线性变换。它们被用于许多不同的数学领域,包括机器学习和人工智能。
在机器学习中,特征值和特征向量用于表示数据、对数据执行操作以及训练机器学习模型。
在人工智能中,特征值和特征向量用于开发图像识别、自然语言处理和机器人等任务的算法。
1. 特征值 (λ):方阵 A 的特征值是一个标量(单个数字)λ,使得存在一个非零向量 v(特征向量),其中以下等式成立:
AV = λv
换句话说,当您将矩阵 A 乘以特征向量 v 时,您会得到一个新向量,它只是 v 的缩放版本(按特征值 λ 缩放)。
2.特征向量:上面提到的向量v称为特征值λ对应的特征向量。特征向量仅在乘以矩阵 A 时改变尺度(大小);他们的方向保持不变。
从数学上讲,要找到特征值和特征向量,您通常可以求解以下方程来得到 λ 和 v:
(A — λI)v = 0
在哪里:
- A 是您要查找特征值和特征向量的方阵。
- λ 是您要查找的特征值。
- I 是单位矩阵(对角线上有 1,其他地方有 0 的对角矩阵)。
- v 是您要查找的特征向量。
求解该方程涉及找到使矩阵 (A — λI) 奇异(即其行列式为零)的 λ 值,然后找到相应的 v 向量。
特征值和特征向量在机器学习和人工智能中的使用:
- 降维 (PCA):在主成分分析 (PCA) 中,您可以计算数据协方差矩阵的特征向量和特征值。具有最大特征值的特征向量(主成分)捕获数据中的最大方差,可用于降低数据集的维数,同时保留重要信息。
- 图像压缩:特征向量和特征值用于图像压缩的奇异值分解 (SVD) 等技术。通过用特征向量和特征值来表示图像,您可以减少存储需求,同时保留基本的图像特征。
- 支持向量机:支持向量机 (SVM) 是一种机器学习算法,可用于分类和回归任务。SVM 的工作原理是找到一个将数据分为两类的超平面。SVM的核矩阵的特征值和特征向量可以用来提高算法的性能。
- 图论:特征向量在分析网络和图方面发挥着作用。它们可用于查找社交网络或其他互连系统中的重要节点或社区。
- 自然语言处理 (NLP):在 NLP 中,特征向量可以帮助识别大型文档术语矩阵中最相关的术语,从而支持用于文档检索和文本摘要的潜在语义分析 (LSA) 等技术。
- 机器学习算法:特征值和特征向量可用于分析机器学习算法的稳定性和收敛性,特别是在深度学习中处理神经网络中的权重矩阵时。
特征值和特征向量的示例
示例 1:主成分分析 (PCA)
PCA是机器学习和数据分析中广泛使用的降维技术。它利用特征向量和特征值来减少特征数量,同时保留尽可能多的信息。
假设您有一个包含两个变量 X 和 Y 的数据集,并且您希望将其减少到一维。您计算数据的协方差矩阵并找到其特征向量和特征值。假设您获得以下内容:
- 特征值 1 (λ₁) = 5
- 特征值 2 (λ2) = 1
- 特征向量 1 (v₁) = [0.8, 0.6]
- 特征向量 2 (v2) = [-0.6, 0.8]
在 PCA 中,您将选择与最大特征值对应的特征向量作为主成分。在这种情况下,它是 v₁。您将数据投影到该特征向量上以将其减少到一维,从而有效地捕获数据中的大部分方差。
示例 2:使用奇异值分解 (SVD) 进行图像压缩
SVD 是一种矩阵分解技术,利用特征值和特征向量进行图像压缩。
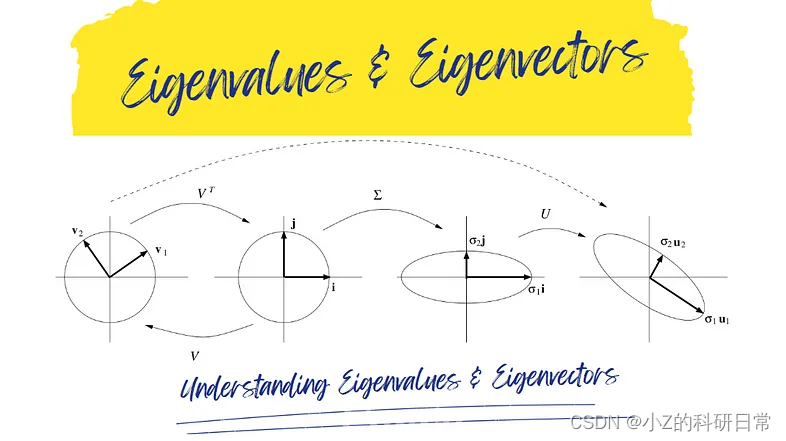
考虑表示为矩阵 A 的灰度图像。对此矩阵执行 SVD 以获得三个矩阵:U(左奇异向量)、Σ(奇异值对角矩阵)和 V^T(右奇异向量)。
- Σ 中的奇异值代表每个分量在重建图像中的重要性。
- U 和 V^T 的列是 A 的协方差矩阵的特征向量。
通过仅保留奇异值的子集(及其相应的特征向量),您可以在压缩图像的同时保留其基本特征。这通常用于图像存储和传输等应用。
示例 3:Google PageRank 算法
特征向量在 Google 的 PageRank 算法中发挥着重要作用,该算法决定了网页在搜索结果中的重要性。在此算法中,网页表示为图中的节点,页面之间的超链接创建一个矩阵。
该矩阵的主特征向量表示网页的 PageRank 分数。相应的特征值有助于确定网页的整体重要性。这使得谷歌可以根据重要性对网页进行排名,帮助用户找到相关内容。
相关文章:

特征值和特征向量及其在机器学习中的应用
特征值和特征向量是线性代数中的概念,用于分析和理解线性变换,特别是由方阵表示的线性变换。它们被用于许多不同的数学领域,包括机器学习和人工智能。 在机器学习中,特征值和特征向量用于表示数据、对数据执行操作以及训练机器学…...

【Vue3】Ref 和 ShallowRef 的区别
这里写自定义目录标题 什么是 Ref什么是 ShallowRef区别对比示例代码 什么是 Ref Ref 是 Vue 3 中的一个新的基本响应式数据类型,它允许我们包装任意的 JavaScript 值,并且在数据变化时发出通知。Ref 提供了一个 .value 属性来访问其内部的值࿰…...
Linux - 进程概念
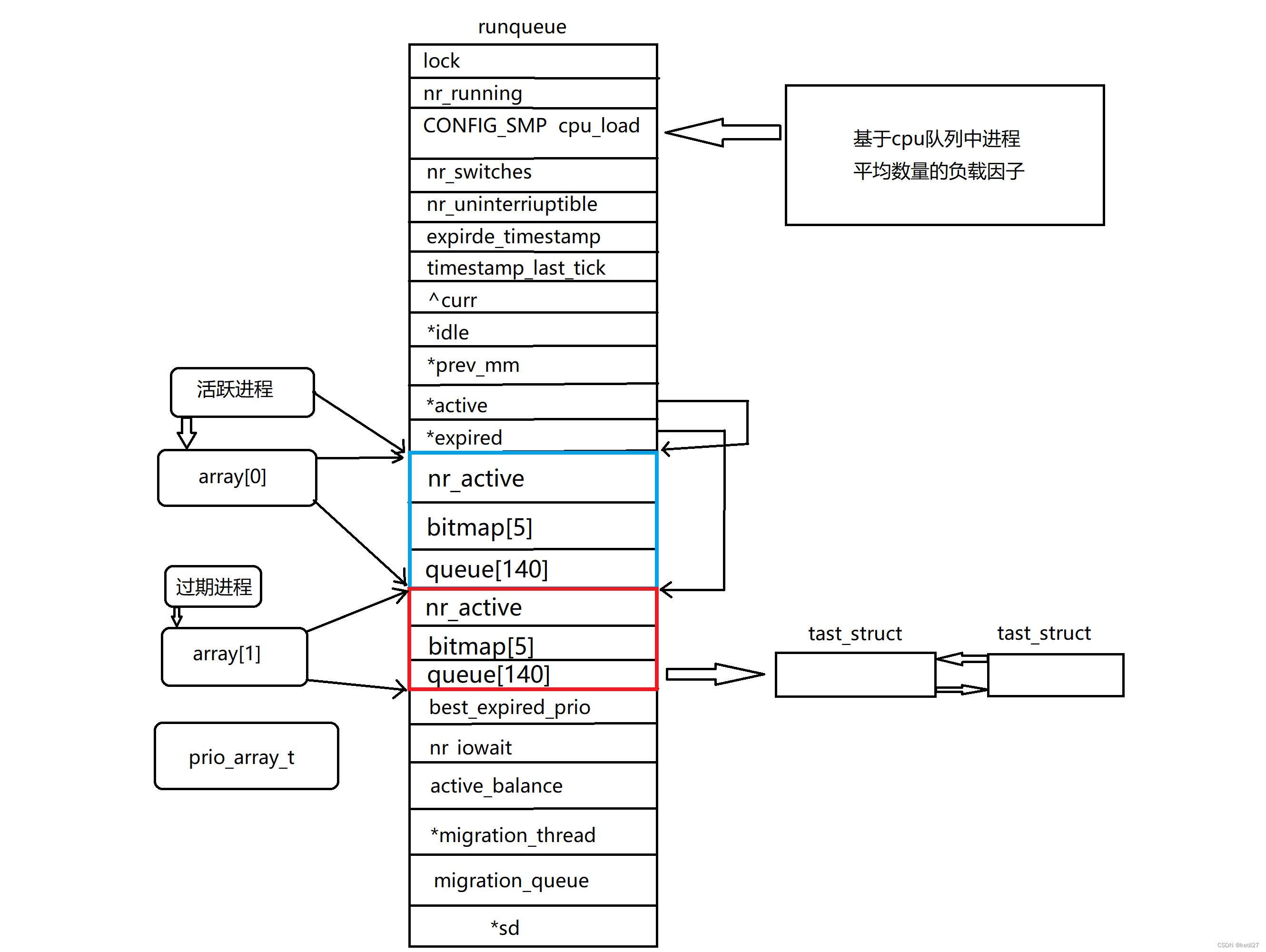
1、冯诺依曼体系结构 我们常见的计算机,如笔记本。我们不常见的计算机,如服务器,大部分都遵守冯诺依曼体系; 截至目前,我们所认识的计算机,都是有一个个的硬件组件组成: 输入单元:…...
H5小游戏,象棋
H5小游戏源码、JS开发网页小游戏开源源码大合集。无需运行环境,解压后浏览器直接打开。有需要的,私信本人,发演示地址,可以后再订阅,发源码,含60+小游戏源码。如五子棋、象棋、植物大战僵尸、开心消消乐、扑鱼达人、飞机大战等等 <!DOCTYPE html PUBLIC "-//W3C/…...
LLM春招准备(1)
llm排序 GPT4V GPT-4V可以很好地理解直接绘制在图像上的视觉指示。它可以直接识别叠加在图像上的不同类型的视觉标记作为指针,例如圆形、方框和手绘(见下图)。虽然GPT-4V能够直接理解坐标,但相比于仅文本坐标,GPT-4V在…...

网络安全知识点总结
1、常见的网络攻击有哪些? 答:(1)口令攻击:也就是窃取用户的账户和密码,普通用户习惯于设置简单的密码,且多个系统用同一套密码,黑客可以使用字典攻击(常用密码库&#…...

服务完善的智能组网系统?
智能组网是现代信息技术的重要组成部分,它通过将各种设备和计算机连接起来,实现高效的数据传输和远程通信。在一个全球化、高度互联的时代背景下,智能组网已经成为了各行各业的必需品。传统的组网方案往往面临着许多问题和挑战。为了解决这些…...
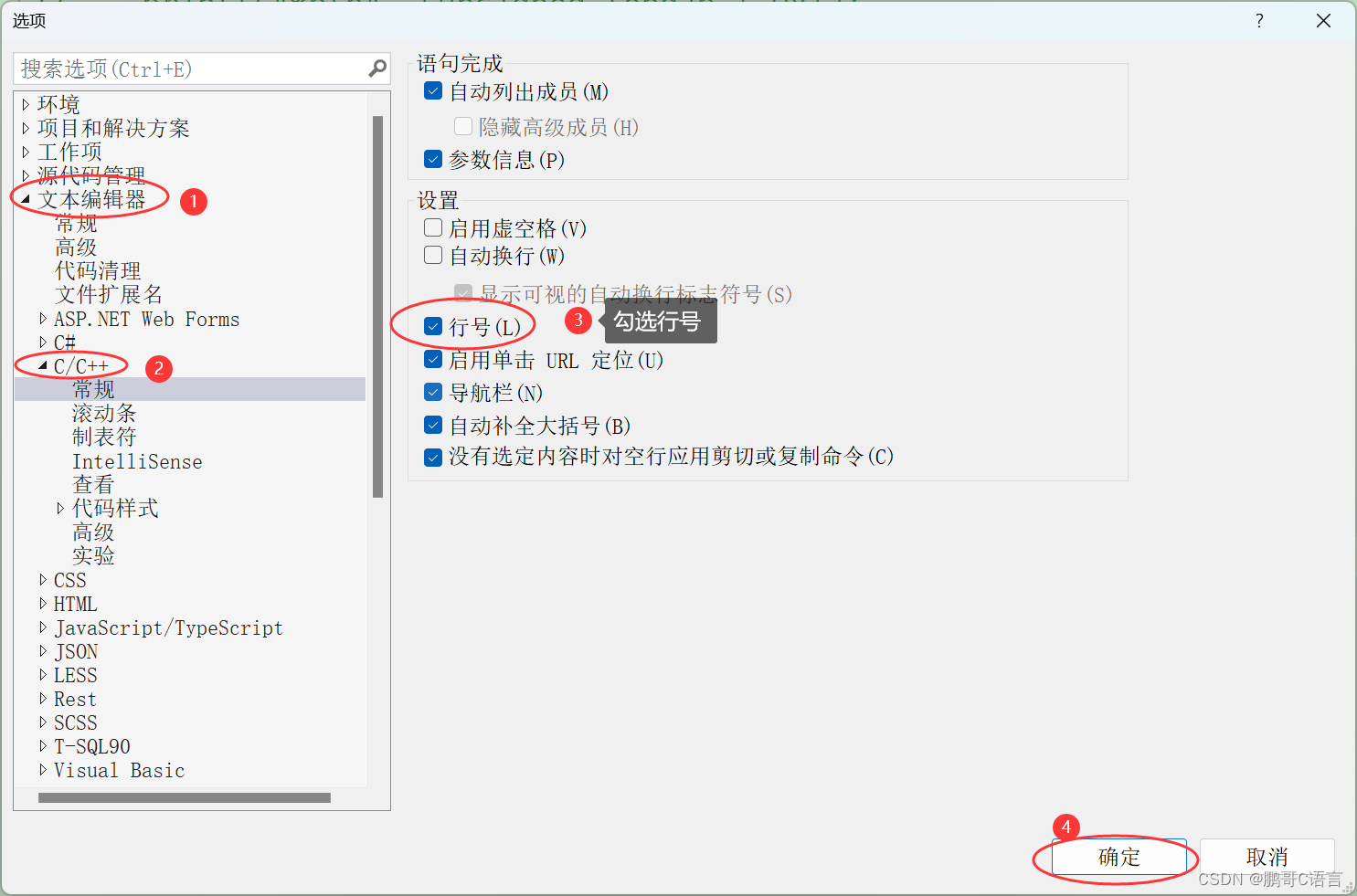
VS2022如何添加行号?(VS2022不显示行号解决方法)
VS2022不显示行号解决方法 VS2022是非常好用的工具,很多同学在初学C/C的时候,都会安装,默认安装好VS2022后,写代码时,在编辑框的窗口左边就有显示行号,如下图所示: 但是有些同学安装好后&#…...

125.验证回文字符串
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。 字母和数字都属于字母数字字符。 给你一个字符串 s,如果它是 回文串 ,返回 true ;否则&#…...
)
Spring Boot的启动流程(个人总结,仅供参考)
SpringBoot应用程序的启动流程主要包括初始化SpringApplication和运行SpringApplication两个过程。 1.初始化SpringApplication包括配置基本的环境变量、资源、构造器和监听器,初始化阶段的主要作用是为运行SpringApplication实例对象启动环境变量准备以及进行必要的…...
用BIO实现tomcat
一、前言 本课程的难度较高,需要将Servlet原理和IO课程全部学完。 二、当前项目使用方式 (1).自定义servlet 自定义servlet需要实现WebServlet并且实现name和urlMapping 重启进行访问 http://localhost:8090/myServlet (2).自定义html 重启进行访问 http://loc…...
JS逆向进阶篇【去哪儿旅行登录】【下篇-逆向Bella参数JS加密逻辑Python生成】
目录: 每篇前言:引子——本篇目的1、 代码混淆和还原(1)单独替换:(2)整个js文件替换: 2、算法入口分析3、 深入分析(0)整体分析:(1&am…...
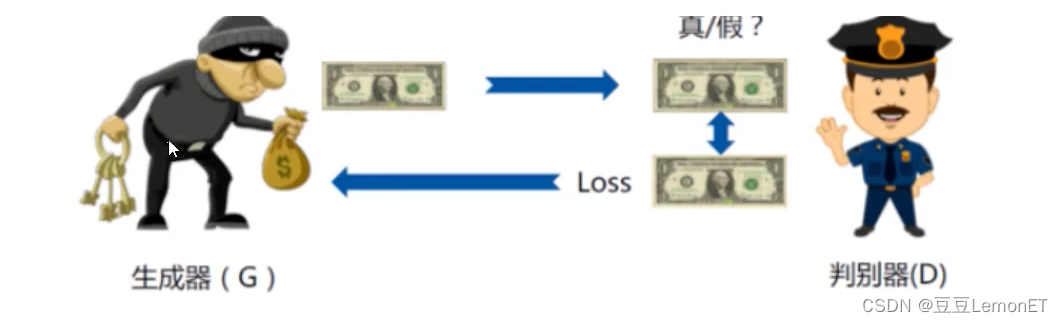
【机器学习】生成对抗网络GAN
概述 生成对抗网络(Generative Adversarial Network,GAN)是一种深度学习模型架构,由生成器(Generator)和判别器(Discriminator)两部分组成,旨在通过对抗训练的方式生成逼…...
centos7安装kafka、zookeeper
安装jdk 安装jdk8 安装zookeeper 在指定目录执行下载命令 我是在/newdisk/zookeeper目录下 wget https://archive.apache.org/dist/zookeeper/zookeeper-3.5.8/apache-zookeeper-3.5.8-bin.tar.gz --no-check-certificate下载好后并解压 tar -zxvf apache-zookeeper-3.5…...
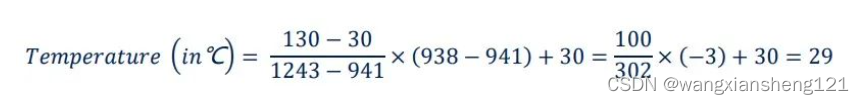
基于 STM32U5 片内温度传感器正确测算温度
目录预览 1、引言 2、问题 3、小结 01 引言 STM32 在内部都集成了一个温度传感器,STM32U5 也不例外。这个位于晶圆上的温度传感器虽然不太适合用来测量外部环境的温度,但是用于监控晶圆上的温度还是挺好的,以防止芯片过温运行。 02 问题…...
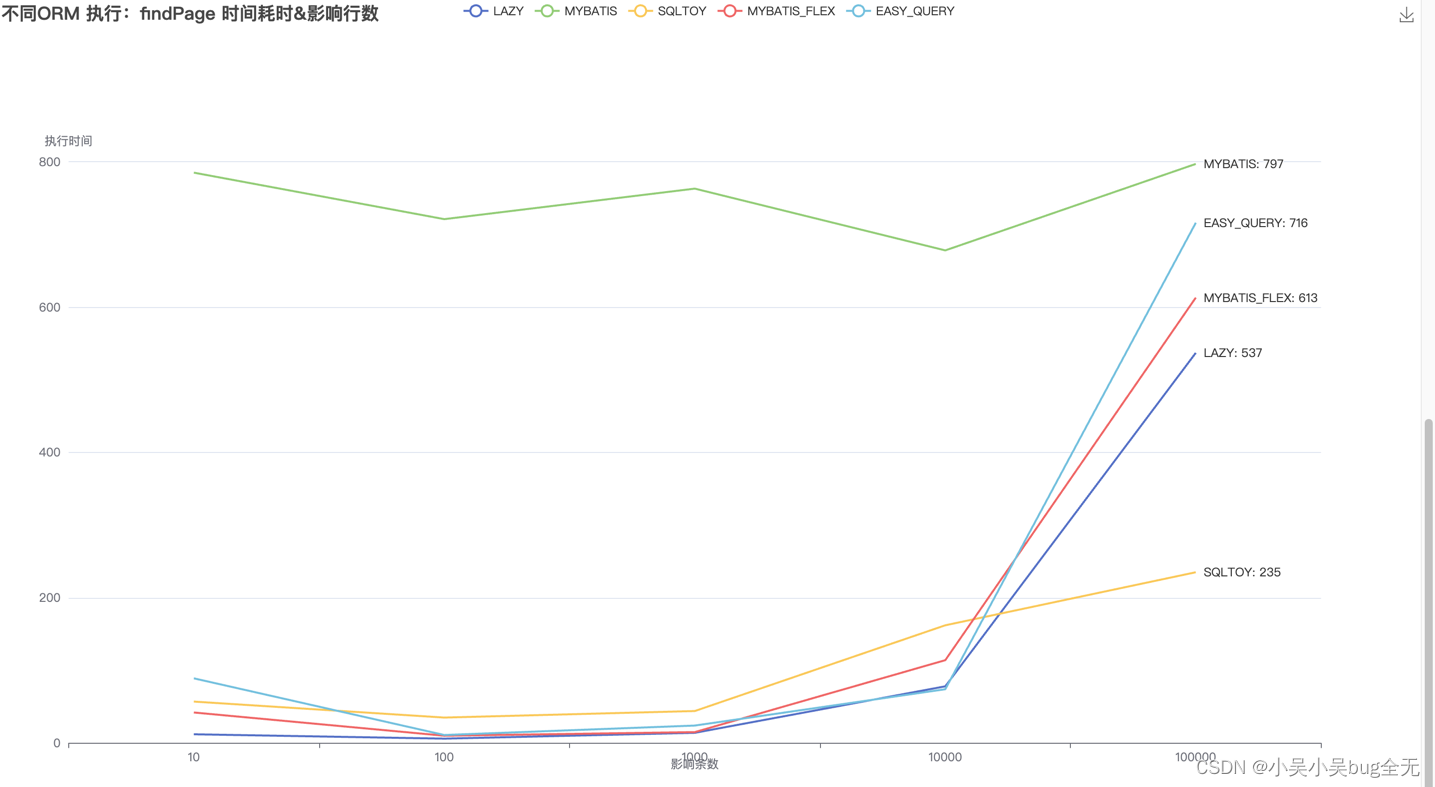
【比较mybatis、lazy、sqltoy、mybatis-flex、easy-query操作数据】操作批量新增、分页查询(三)
orm框架使用性能比较 比较mybatis、lazy、sqltoy、mybatis-flex、easy-query操作数据 环境: idea jdk17 spring boot 3.0.7 mysql 8.0测试条件常规对象 orm 框架是否支持xml是否支持 Lambda对比版本mybatis☑️☑️3.5.4sqltoy☑️☑️5.2.98lazy✖️☑️1.2.4…...

Leetcode 3068. Find the Maximum Sum of Node Values
Leetcode 3068. Find the Maximum Sum of Node Values 1. 解题思路2. 代码实现 题目链接:3068. Find the Maximum Sum of Node Values 1. 解题思路 这一题虽然标记为一道hard的题目,但其实就是一个脑筋急转弯的题目。 我们只需要想明白一点即可&…...

用 Dockerfile为镜像添加SSH服务
1、基础镜像ubuntu:18.04 2、替换为国内的安装源 3、安装openssh-server 4、允许root用户远程登陆 5、暴露端口22 6、服务开机自启动 1.创建目录 [rootopenEuler-node1 db]# mkdir sshd_ubuntu 2.创建 Dockerfile、 run.sh 、authorized_keys、vim aliyun.list 文件 [rootop…...

Maven能解决什么问题?为什么要用?
如果没有maven,我们在开发一个应用的时候,需要自己先确定要引入哪些第三方的jar包,并且要去找到这些jar包,把他们导入到项目中,而且最痛苦的时候各个jar包之间的兼容性和冲突的问题。 jar包弄好了之后,我们…...

【Golang星辰图】探索网络和HTTP的奇妙世界:使用Go语言打造高性能应用
提升Web开发效率:学会使用Go语言的网络和HTTP库 前言 随着互联网的快速发展,网络和HTTP成为了现代应用开发中必不可少的部分。Go语言作为一门快速、可靠和高效的编程语言,提供了丰富的网络编程和HTTP处理库,使得构建高性能的网络…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...
