python实现常见一元随机变量的概率分布
一. 随机变量
随机变量是一个从样本空间 Ω \Omega Ω到实数空间 R R R的函数,比如随机变量 X X X可以表示投骰子的点数。随机变量一般可以分为两类:
- 离散型随机变量:随机变量的取值为有限个。
- 连续型随机变量:随机变量的取值是连续的,有无限多个。
scipy.stat模块中包含了多种概率分布的随机变量,包含离散型随机变量和连续型随机变量。离散型随机变量的常见接口如下:
| 方法名 | 功能 |
|---|---|
| rvs | 生成该分布的随机序列 |
| pmf | 概率质量函数 |
| cdf | 累计概率分布函数 |
| stats | 计算该分布的均值,方差,偏度,峰度。[Mean(‘m’), variance(‘v’), skew(‘s’), kurtosis(‘k’)] |
连续型随机变量的常见接口如下:
| 方法名 | 功能 |
|---|---|
| rvs | 生成该分布的随机序列 |
| 概率密度函数 | |
| cdf | 累计概率分布函数 |
| stats | 计算该分布的均值,方差,偏度,峰度。[Mean(‘m’), variance(‘v’), skew(‘s’), kurtosis(‘k’)] |
二. 常见离散分布
1. 二项分布
如果随机变量 X X X的分布律为 P ( X = k ) = C n k p k q n − k , k = 0 , 1 , . . . n , P(X=k) = C^k_np^kq^{n-k},k = 0,1,...n, P(X=k)=Cnkpkqn−k,k=0,1,...n,其中 p + q = 1 p + q = 1 p+q=1 ,则称 X X X服从参数为 n , p n,p n,p的二项分布,记为 X ∼ B ( n , p ) X \sim B(n,p) X∼B(n,p)。
- 期望: E ( X ) = n p E(X) = np E(X)=np
- 方差: D ( X ) = n p ( 1 − p ) D(X) = np(1 - p) D(X)=np(1−p)
-
画出不同参数下的二项分布, n , p n, p n,p分别为 ( 10 , 0.3 ) , ( 10 , 0.5 ) , ( 10 , 0.7 ) (10,0.3),(10,0.5),(10,0.7) (10,0.3),(10,0.5),(10,0.7)
import numpy as np from scipy.stats import binom import matplotlib.pyplot as pltplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(3, 1, figsize = (10, 10))# 调整子图间距fig.subplots_adjust(hspace = 0.5)params = [(10, 0.3), (10, 0.5), (10, 0.7)]for i in range(len(params)):n = params[i][0]p = params[i][1]x = np.arange(0, n + 1)y = binom(n, p).pmf(x)# 计算随机变量的期望,方差mean, var = binom.stats(n, p, moments='mv')ax[i].scatter(x, y, color = 'blue', marker = 'o')ax[i].set_title('n = {}, p = {}'.format(n, p))ax[i].set_xticks(x)ax[i].text(1, 0.2, '期望: {:.2f}\n方差: {:.2f}'.format(mean, var))ax[i].grid()plt.show()运行结果:

-
生成服从不同参数二项分布的随机数组(采样100000次),然后查看数组的频率分布
import numpy as np from scipy.stats import binom import matplotlib.pyplot as pltplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(3, 1, figsize = (10, 10))# 调整子图间距fig.subplots_adjust(hspace = 0.5)params = [(10, 0.3), (10, 0.5), (10, 0.7)]for i in range(len(params)):n = params[i][0]p = params[i][1]x = np.arange(0, 11)# 抽样10万次sample = binom.rvs(n = n, p = p, size = 100000)print(sample)ax[i].hist(sample, color = 'blue', density=True, bins = 50)ax[i].set_title('n = {}, p = {}'.format(n, p))ax[i].set_xticks(x)ax[i].grid()plt.show()运行结果:

2. 几何分布
若随机变量 X X X的分布律为 P ( X = k ) = ( 1 − p ) k − 1 p , k = 1 , 2 , . . . , P(X = k) = (1 - p)^{k - 1}p,k = 1, 2, ..., P(X=k)=(1−p)k−1p,k=1,2,...,其中 0 < p < 1 0 < p < 1 0<p<1,则称 X X X服从参数为 p p p的几何分布,记为 X ∼ G e ( p ) X \sim Ge(p) X∼Ge(p)。
- 期望: E ( X ) = 1 p E(X) = \frac{1}{p} E(X)=p1
- 方差: D ( X ) = 1 − p p 2 D(X) = \frac{1 - p}{p^2} D(X)=p21−p
-
画出不同参数下的几何分布, p p p分别为 ( 0.3 , 0.5 , 0.7 ) (0.3,0.5,0.7) (0.3,0.5,0.7)
import numpy as np from scipy.stats import geom import matplotlib.pyplot as pltplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(3, 1, figsize = (10, 10))# 调整子图间距fig.subplots_adjust(hspace = 0.5)params = [0.3,0.5,0.7]for i in range(len(params)):p = params[i]x = np.arange(1, 15)y = geom(p = p).pmf(x)print(y)# 计算随机变量的期望,方差mean, var = geom.stats(p = p, moments='mv')ax[i].scatter(x, y, color = 'blue', marker = 'o')ax[i].set_title('p = {}'.format(p))ax[i].set_xticks(x)ax[i].text(5, 0.2, '期望: {:.2f}\n方差: {:.2f}'.format(mean, var))ax[i].grid()plt.show()运行结果:

-
生成服从不同参数几何分布的随机数组(采样100000次),然后查看数组的频率分布
import numpy as np from scipy.stats import geom import matplotlib.pyplot as pltplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(3, 1, figsize = (10, 10))# 调整子图间距fig.subplots_adjust(hspace = 0.5)params = [0.3, 0.5, 0.7]for i in range(len(params)):p = params[i]x = np.arange(0, 15)# 抽样sample = geom.rvs(p = p, size = 100000)print(sample)ax[i].hist(sample, color = 'blue', density=True, bins = 50)ax[i].set_title('p = {}'.format(p))ax[i].set_xlim(0,15)ax[i].set_xticks(x)ax[i].grid()plt.show()运行结果:

3. 泊松分布
若随机变量 X X X的分布律为 P ( X = k ) = λ k k ! e − λ , k = 0 , 1 , 2... , P(X=k) = \frac{\lambda^k}{k!}e^{-\lambda},k = 0, 1, 2 ..., P(X=k)=k!λke−λ,k=0,1,2...,其中 λ > 0 , \lambda > 0, λ>0,则称 X X X服从参数为 λ \lambda λ的泊松分布,记为 X ∼ P ( λ ) X \sim P(\lambda) X∼P(λ)。
- 期望: E ( X ) = λ E(X) = \lambda E(X)=λ
- 方差: D ( X ) = λ D(X) = \lambda D(X)=λ
-
画出不同参数下的泊松分布, λ \lambda λ分别为 ( 2 , 6 , 8 ) (2,6,8) (2,6,8)
import numpy as np from scipy.stats import poisson import matplotlib.pyplot as pltplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(3, 1, figsize = (10, 10))# 调整子图间距fig.subplots_adjust(hspace = 0.5)params = [2,6,8]for i in range(len(params)):numda = params[i]x = np.arange(1, 15)y = poisson(numda).pmf(x)# 计算随机变量的期望,方差mean, var = poisson.stats(numda, moments='mv')ax[i].scatter(x, y, color = 'blue', marker = 'o')ax[i].set_title('lambda = {}'.format(numda))ax[i].set_xticks(x)ax[i].set_yticks([0, 0.1, 0.2, 0.3, 0.4])ax[i].text(5, 0.2, '期望: {:.2f}\n方差: {:.2f}'.format(mean, var))ax[i].grid()plt.show()运行结果:

-
生成服从不同参数泊松分布的随机数组(采样100000次),然后查看数组的频率分布
import numpy as np from scipy.stats import poisson import matplotlib.pyplot as pltplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(3, 1, figsize = (10, 10))# 调整子图间距fig.subplots_adjust(hspace = 0.5)params = [2, 6, 8]for i in range(len(params)):numda = params[i]x = np.arange(0, 16)# 抽样sample = poisson.rvs(numda, size = 1000000)print(sample)ax[i].hist(sample, color = 'blue', density=True, bins = 50)ax[i].set_title('lamdba = {}'.format(numda))ax[i].set_xticks(x)ax[i].set_xlim(0, 16)ax[i].grid()plt.show()运行结果:

三. 常见连续分布
1. 正太分布
若随机变量 X X X的概率密度函数为 f ( x ) = 1 2 π δ e − ( x − μ ) 2 2 δ 2 , ( − ∞ < x < + ∞ ) f(x) = \frac{1}{\sqrt{2\pi}\delta}e^{- \frac{(x - \mu)^2}{2\delta^2}},( -\infty< x < +\infty) f(x)=2πδ1e−2δ2(x−μ)2,(−∞<x<+∞),则称 X X X服从参数为 ( μ , δ 2 ) (\mu,\delta^2) (μ,δ2)的正太分布,记为 X ∼ N ( μ , δ 2 ) X \sim N(\mu,\delta^2) X∼N(μ,δ2)。当 μ = 0 , δ = 1 \mu =0,\delta = 1 μ=0,δ=1时称 X X X服从标准正太分布。
- 期望: E ( X ) = μ E(X) = \mu E(X)=μ
- 方差: D ( X ) = δ 2 D(X) = \delta^2 D(X)=δ2
-
画出不同参数下的正太分布, μ , δ \mu,\delta μ,δ分别为 ( 0 , 1 ) , ( 0 , 3 ) (0, 1), (0, 3) (0,1),(0,3)
import numpy as np from scipy.stats import norm import matplotlib.pyplot as pltplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(figsize=(10, 8))params = [(0, 1, 'red'), (0, 3, 'blue')]x = np.linspace(-20, 20, 1000)for i in range(0, len(params)):loc = params[i][0]scale = params[i][1]color = params[i][2]mean, var = norm.stats(loc, scale, moments='mv')ax.plot(x, norm(loc = loc, scale = scale).pdf(x), color = color, label = 'loc={},scale={},均值={},方差={}'.format(loc, scale,mean,var))ax.set_xticks(np.arange(-20, 21))ax.grid()ax.legend()plt.show()运行结果:

-
生成服从不同参数正太分布的随机数组(采样100000次),然后查看数组的频率分布
import numpy as np from scipy.stats import norm import matplotlib.pyplot as pltplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(2, 1, figsize=(10, 8))params = [(0, 1, 'red'), (0, 3, 'blue')]x = np.linspace(-20, 20, 1000)# 采样for i in range(0, len(params)):loc = params[i][0]scale = params[i][1]color = params[i][2]# 画出分布图ax[i].plot(x, norm(loc = loc, scale = scale).pdf(x), color = color, label = 'loc={},scale={}'.format(loc, scale))# 画出随机抽样的频率分布直方图ax[i].hist(norm(loc = loc, scale = scale).rvs(size = 100000), density=True, bins = 100)ax[i].set_xticks(np.arange(-20, 21))ax[i].grid()ax[i].legend()plt.show()运行结果:

2. 指数分布
若随机变量 X X X的概率密度函数为 f ( x ) = { λ e − λ x x ≥ 0 0 x < 0 ( λ > 0 ) f(x) = \begin{cases} {\lambda}e^{-{\lambda}x} & x \ge 0\\0 & x < 0\end{cases} (\lambda > 0) f(x)={λe−λx0x≥0x<0(λ>0),则称 X X X服从参数为 λ \lambda λ的指数分布,记为 X ∼ E ( λ ) X \sim E(\lambda) X∼E(λ)。
- 期望: E ( X ) = 1 λ E(X) = \frac{1}{\lambda} E(X)=λ1
- 方差: D ( X ) = 1 λ 2 D(X) = \frac{1}{{\lambda}^2} D(X)=λ21
scipy中指数分布expon的参数传入 λ \lambda λ的倒数。
A common parameterization for expon is in terms of the rate parameter lambda, such that pdf = lambda * exp(-lambda * x). This parameterization corresponds to using scale = 1 / lambda.
-
画出不同参数下的指数分布, λ \lambda λ分别为 ( 0.5 , 1 , 1.5 ) (0.5,1,1.5) (0.5,1,1.5)
import numpy as np import matplotlib.pyplot as plt from scipy.stats import exponplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(figsize = (10, 8))params = [(0.5, 'red'), (1, 'blue'), (1.5, 'green')]x = np.linspace(0, 15, 1000)for i in range(0, len(params)):numda = params[i][0]color = params[i][1]mean, var = expon.stats(loc = 0, scale = 1 / numda, moments='mv')ax.plot(x, expon(scale = 1 / numda).pdf(x), color = color, label = 'lambda = {:.2f}, 均值:{:.2f}, 方差: {:.4f}'.format(numda, mean, var))ax.grid()ax.legend()plt.show()运行结果:

-
生成服从不同参数指数分布的随机数组(采样100000次),然后查看数组的频率分布
import numpy as np import matplotlib.pyplot as plt from scipy.stats import exponplt.rcParams["font.family"] = "SimHei" # 设置字体 plt.rcParams["axes.unicode_minus"] = False # 正常显示负号if __name__ == '__main__':fig, ax = plt.subplots(3, 1, figsize = (10, 8))params = [(0.5, 'red'), (1, 'blue'), (1.5, 'green')]x = np.linspace(0, 15, 1000)# 采样for i in range(0, len(params)):numda = params[i][0]color = params[i][1]ax[i].plot(x, expon(scale = 1/numda).pdf(x), color = color, label = 'lambda={}'.format(numda))ax[i].hist(expon(scale = 1/numda).rvs(size = 10000), density=True, bins = 100)ax[i].set_xticks(np.arange(0, 15))ax[i].set_xlim(0, 15)ax[i].grid()ax[i].legend()plt.show()运行结果:

相关文章:

python实现常见一元随机变量的概率分布
一. 随机变量 随机变量是一个从样本空间 Ω \Omega Ω到实数空间 R R R的函数,比如随机变量 X X X可以表示投骰子的点数。随机变量一般可以分为两类: 离散型随机变量:随机变量的取值为有限个。连续型随机变量:随机变量的取值是连…...
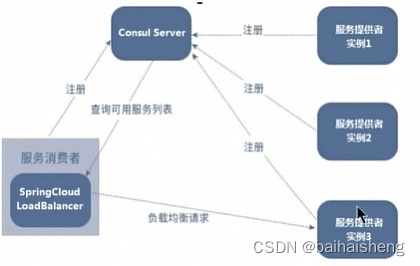
微服务学习
SpringCloud组成 服务注册与发现:consul 阿里Nacos 服务调用和负载均衡:OpenFeign LoadBalance 分布式事务:阿里Seata 服务熔断和降级:阿里Sentinel Circuit Breaker 服务链路追踪:Micrometer Tracing 服务网关:GateWa…...

【.NET Core】深入理解IO - 读取器和编写器
【.NET Core】深入理解IO - 读取器和编写器 文章目录 【.NET Core】深入理解IO - 读取器和编写器一、概述二、BinaryReader和BinaryWriter2.1 BinartReader类2.2 BinaryWriter类 三、StreamReader和StreamWriter3.1 StreamReader类3.1 StreamWriter类StreamWriter类构造函数Str…...
【Java项目介绍和界面搭建】拼图小游戏——添加图片
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【Java】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏 …...

「MySQL」基本操作类型
🎇个人主页:Ice_Sugar_7 🎇所属专栏:数据库 🎇欢迎点赞收藏加关注哦! 数据库的操作 创建、显示数据库 使用 create 创建一个数据库 create database goods;然后可以用 show databases 来查看已经创建的数…...

Android 14 权限
问题Android 14 按照视频播放类的应用 无法获取到权限。 原因是从 Android 13 开始,如果你的应用程序 targetSdk 指定到了 33 或以上,那么 READ_EXTRERNAL_STORGE 权限就完全失去了作用,申请它将不会产生任何效果。 与此相对应的,…...

Springboot整合SSE实现实时消息推送
SSE详细介绍传送门:SSE实时消息推送 简单描述一下SSE推送在实际项目中应用的常见场景 1,项目页面中有消息通知板块,当信息有变化时,只有手动刷新页面,才会看到最新的数据,这里可以采用SSE技术实时推送最新…...

在pytorch中利用GPU训练神经网络时代码的执行顺序并提高训练效率
在pytorch中利用GPU训练神经网络时代码的执行顺序并提高训练效率 在 PyTorch 中,大多数操作在 GPU 上默认是异步执行的,但这并不意味着它们是并行执行的。要理解代码是同步还是异步执行,以及是串行还是并行执行,我们需要考虑几个…...
vue3学习
距离vue2学习已经一年度了,现在开始vue3的学习。 一、webpack (1)创建列表隔行变色项目及webpack使用: 新建项目空白目录,并运行npm init -y命令,初始化包管理配置文件package.json; 新建sr…...

毫秒生成的时间戳如何转化成东八区具体时间
假设现在有一个时间是1709101071419L 后端代码实现 Java代码(东八区时间) 在Java代码中,我们将时区从UTC调整为东八区(UTC8): import java.time.Instant; import java.time.ZoneId; import java.time.Z…...
02. Nginx入门-Nginx安装
Nginx安装 yum安装 编辑yum环境 cat > /etc/yum.repos.d/nginx.repo << EOF [nginx-stable] namenginx stable repo baseurlhttp://nginx.org/packages/centos/$releasever/$basearch/ gpgcheck1 enabled1 gpgkeyhttps://nginx.org/keys/nginx_signing.key module_…...

leetcode73. 矩阵置零
链接见:https://leetcode.cn/problems/set-matrix-zeroes/description/ 题目描述 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 AC代码 class Solution { public:void setZeroes(vec…...
【中间件】RabbitMQ入门
📝个人主页:五敷有你 🔥系列专栏:中间件 ⛺️稳中求进,晒太阳 MQ的优劣: 优势 应用解耦:提升了系统容错性和可维护性异步提速:提升用户体验和系统吞吐量消峰填谷࿱…...
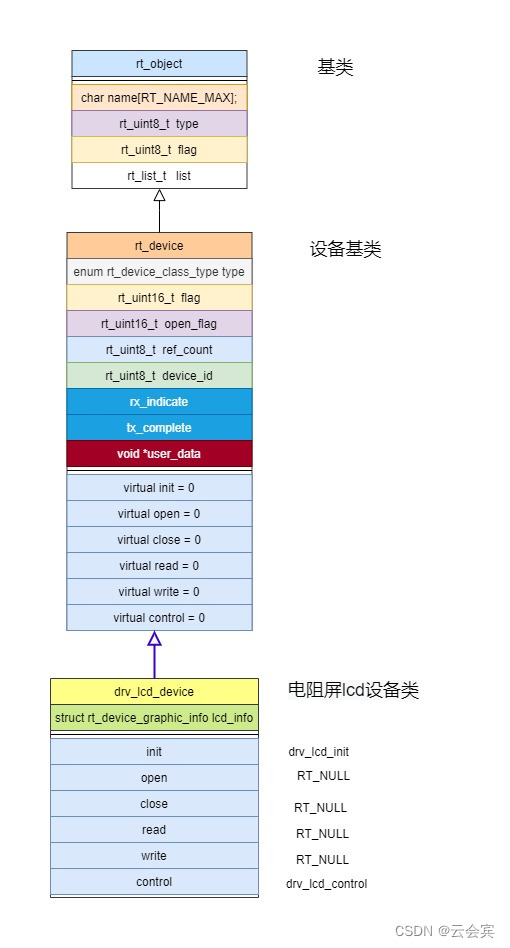
rtt的io设备框架面向对象学习-电阻屏LCD设备
目录 1.8080通信的电阻屏LCD设备1.1 构造流程1.2 使用2.i2c和spi通信的电阻屏LCD 电阻屏LCD通信接口有支持I2c、SPI和8080通信接口的。 1.8080通信的电阻屏LCD设备 lcd这块不像其他设备类,rtt没有实现的设备驱动框架层,那么是在驱动层直接实现的。 以…...
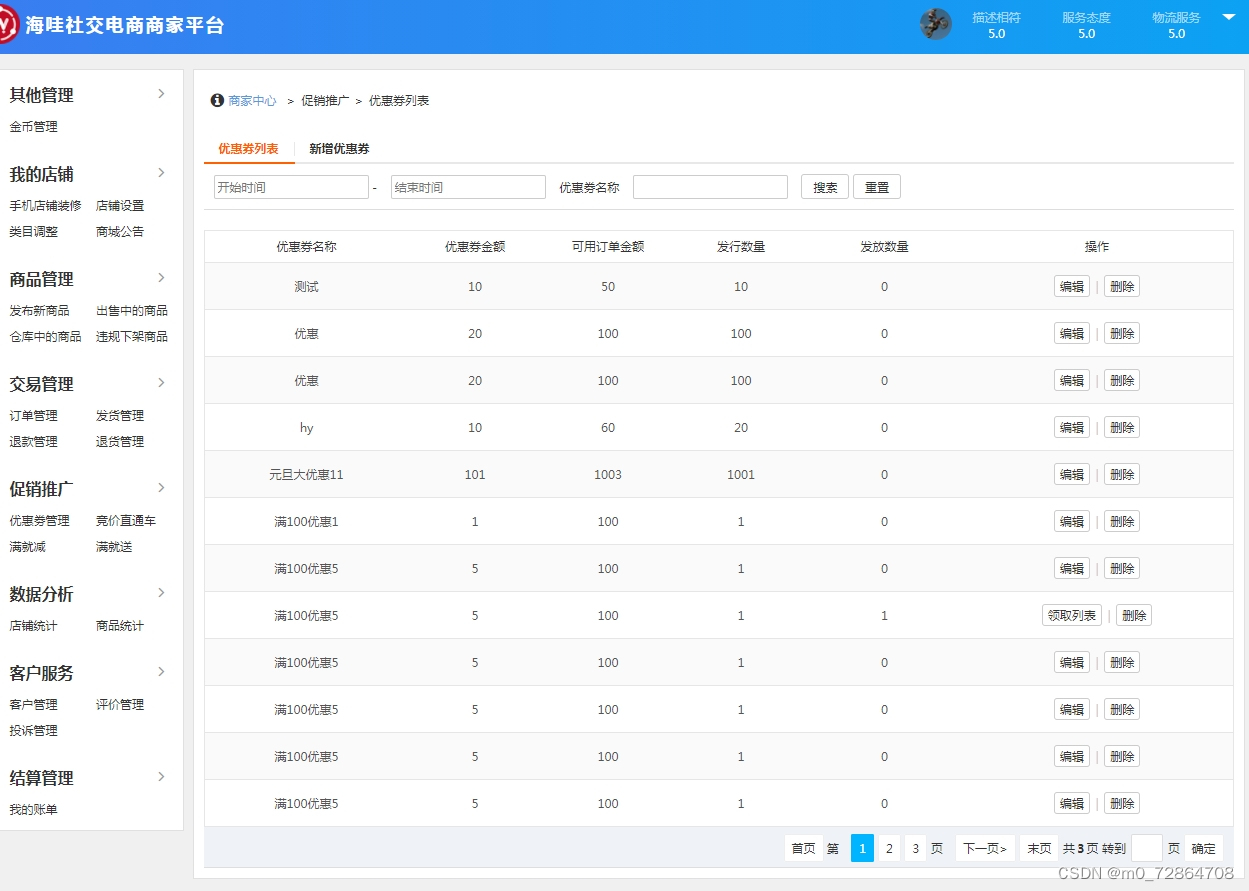
商城免费搭建之java商城 java电子商务Spring Cloud+Spring Boot+mybatis+MQ+VR全景
1. 涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis 3. 前端框架…...

蓝桥杯刷题--python-16
562. 壁画 - AcWing题库 Tint(input()) j1 while(j<T): N int(input()) ainput() s [0]*(N1) # 求前戳和 for i in range(1, N 1): s[i] int(a[i-1]) s[i - 1] # 枚举 # 区间 max_ float(-inf) k (N 2 - 1) // 2 for i in …...

闰年计算中的计算机Bug
不知道你有没有看过凯瑟琳泽塔琼斯主演的《偷天陷阱》,里面主题思想是用银行结算系统的千年虫bug,精心设计,盗取银行几十亿的精彩动作片。所谓2000 年千禧年的千年虫,其实就是计算机计算闰年的bug。 这个闰年计算的历史源远流长&…...
python水表识别图像识别深度学习 CNN
python水表识别,图像识别深度学习 CNN,Opencv,Keras 重点:项目和文档是本人近期原创所作!程序可以将水表图片里面的数据进行深度学习,提取相关信息训练,lw1.3万字重复15%,可以直接上交那种&…...
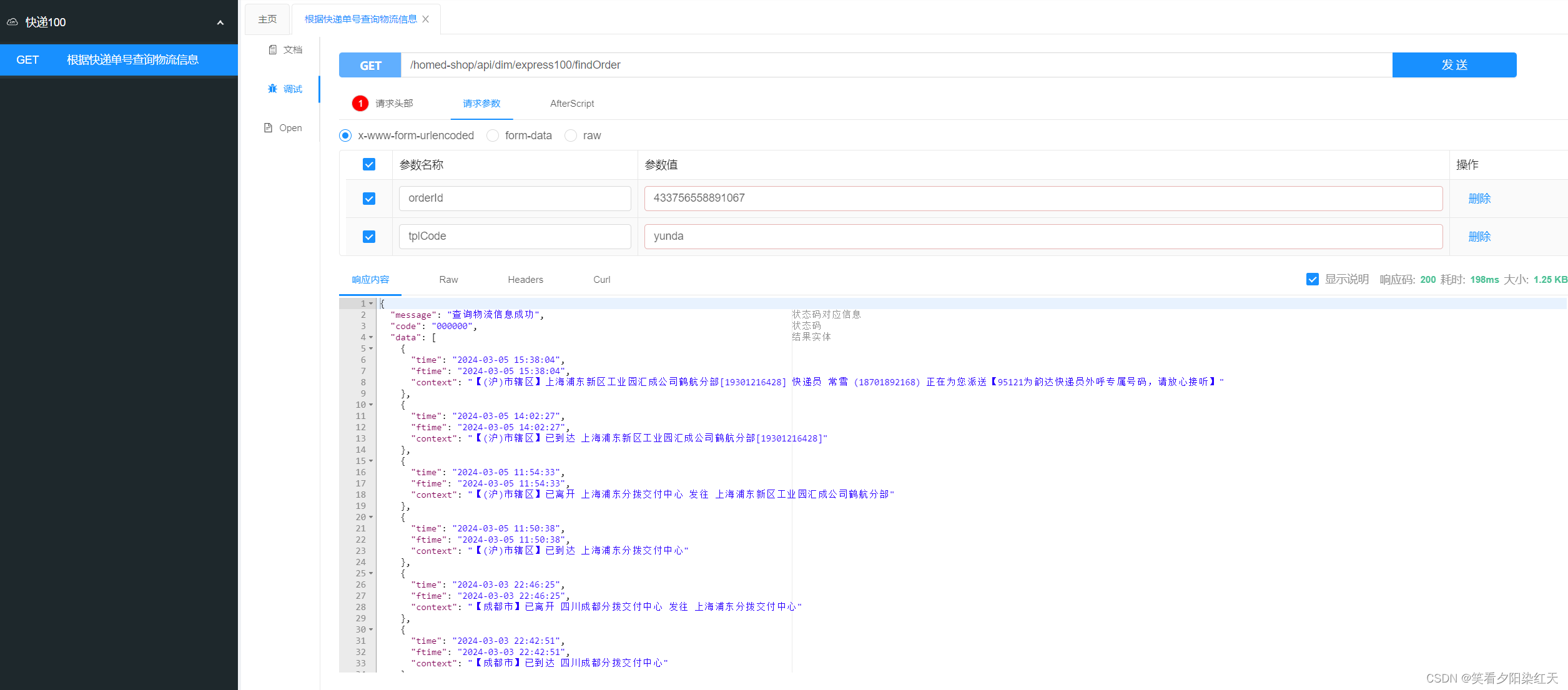
Java对接快递100实时快递单号查询API接口
目录 1.引入依赖 2.定义配置信息 3.模块结构 4.Controller 5.Service实现类 6.返回数据dto以及dto中的数据dto 7.测试运行 今天也是接到了这个任务,官网有小demo,可以下载下来参考test中代码 官方文档地址: 实时快递查询接口技术文档…...
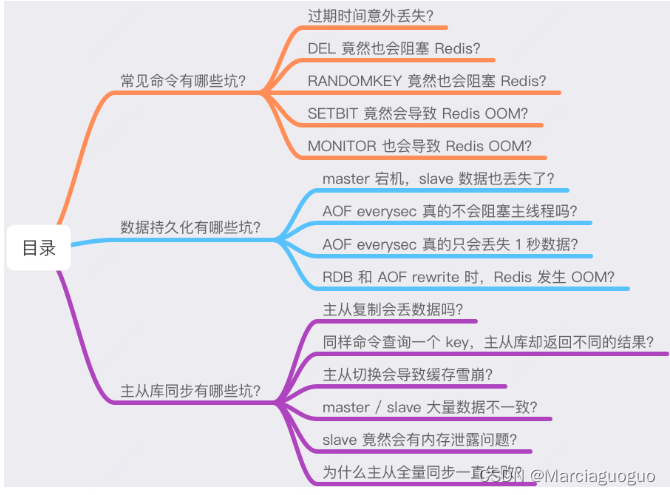
Redis常见的15个【坑】,避坑指南
一、常见命令 1.1 过期时间意外丢失 原因: SET命令如果不设置过期时间,那么Redis会自动【擦除】这个key的过期时间 1.2 DEL命令阻塞redis key是String类型时,DEL时间复杂度是O(1)key是List/Hash/Set/ZSet类型,DEL时间复杂度是…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...

标注工具核心架构分析——主窗口的图像显示
🏗️ 标注工具核心架构分析 📋 系统概述 主要有两个核心类,采用经典的 Scene-View 架构模式: 🎯 核心类结构 1. AnnotationScene (QGraphicsScene子类) 主要负责标注场景的管理和交互 🔧 关键函数&…...

STM32 低功耗设计全攻略:PWR 模块原理 + 睡眠 / 停止 / 待机模式实战(串口 + 红外 + RTC 应用全解析)
文章目录 PWRPWR(电源控制模块)核心功能 电源框图上电复位和掉电复位可编程电压监测器低功耗模式模式选择睡眠模式停止模式待机模式 修改主频一、准备工作二、修改主频的核心步骤:宏定义配置三、程序流程:时钟配置函数解析四、注意…...
