由数据范围反推算法复杂度以及算法内容
一般ACM或者笔试题的时间限制是1秒或2秒。
在这种情况下,C++代码中的操作次数控制在 1 0 7 ∼ 1 0 8 10^7\sim10^8 107∼108为最佳。
下面给出在不同数据范围下,代码的时间复杂度和算法该如何选择:
- n ≤ 30 n\leq30 n≤30,指数级别, d f s + dfs+ dfs+剪枝,状态压缩 d p dp dp;
- n ≤ 100 ⇒ O ( n 3 ) n\leq100\rArr O(n^3) n≤100⇒O(n3), f l o y d floyd floyd, d p dp dp,高斯消元;
- n ≤ 1000 ⇒ O ( n 2 ) n\leq1000\rArr O(n^2) n≤1000⇒O(n2), O ( n 2 l o g n ) O(n^2logn) O(n2logn), d p dp dp,二分,朴素版 D i j k s t r a Dijkstra Dijkstra,朴素版 P r i m Prim Prim, B e l l m a n − F o r d Bellman-Ford Bellman−Ford;
- n ≤ 10000 ⇒ O ( n ∗ x ) n\leq10000\rArr O(n*\sqrt{x}) n≤10000⇒O(n∗x),块状链表、分块、莫队;
- n ≤ 100000 ⇒ O ( n l o g n ) ⇒ n\leq100000\rArr O(nlogn)\rArr n≤100000⇒O(nlogn)⇒,各种 s o r t sort sort,线段树、树状数组、 s e t / m a p set/map set/map、 h e a p heap heap、拓扑排序、 d i j k s t r a + h e a p dijkstra+heap dijkstra+heap、 p r i m + h e a p prim+heap prim+heap、 K r u s k a l Kruskal Kruskal、 s p f a spfa spfa、求凸包、求半平面交、二分、 C D Q CDQ CDQ分治、整体二分、后缀数组、树链剖分、动态树;
- n ≤ 1000000 ⇒ O ( n ) n\leq1000000\rArr O(n) n≤1000000⇒O(n),以及常数较小的 O ( n l o g n ) O(nlogn) O(nlogn)算法 ⇒ \rArr ⇒ 单调队列、 h a s h hash hash、双指针扫描、 B F S BFS BFS、并查集、 k m p kmp kmp、 A C AC AC自动机,常数比较小的 O ( n l o g n ) O(nlogn) O(nlogn)的做法: s o r t sort sort、树状数组、 h e a p heap heap、 d i j k s t r a dijkstra dijkstra、 s p f a spfa spfa;
- n ≤ 10000000 ⇒ O ( n ) n\leq10000000\rArr O(n) n≤10000000⇒O(n),双指针扫描、 k m p kmp kmp、 A C AC AC自动机、线性筛素数;
- n ≤ 1 0 9 ⇒ O ( n ) n\leq10^9\rArr O(\sqrt{n}) n≤109⇒O(n),判断质数;
- n ≤ 1 0 18 ⇒ O ( l o g n ) n\leq10^{18}\rArr O(logn) n≤1018⇒O(logn),最大公约数,快速幂,数位DP;
- n ≤ 1 0 1000 ⇒ O ( ( l o g n ) 2 ) n\leq10^{1000}\rArr O((logn)^2) n≤101000⇒O((logn)2),高精度加减乘除;
- n ≤ 1 0 100000 ⇒ O ( l o g k × l o g l o g k ) n\leq10^{100000}\rArr O(logk\times loglogk) n≤10100000⇒O(logk×loglogk), k k k表示位数,高精度加减, F F T / N T T FFT/NTT FFT/NTT。
相关文章:

由数据范围反推算法复杂度以及算法内容
一般ACM或者笔试题的时间限制是1秒或2秒。 在这种情况下,C代码中的操作次数控制在 1 0 7 ∼ 1 0 8 10^7\sim10^8 107∼108为最佳。 下面给出在不同数据范围下,代码的时间复杂度和算法该如何选择: n ≤ 30 n\leq30 n≤30,指数级别…...

js监听F11触发全屏事件
当用户使用 F11 键进行浏览器全屏时,由于此时并非通过浏览器提供的 Fullscreen API 进入全屏模式,因此无法通过 fullscreenchange 事件来监听全屏状态的变化。在这种情况下,可以通过监听 resize 事件来检测浏览器窗口大小的变化,从…...

Seata 2.x 系列【1】专栏导读
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 3.1.0 本系列Seata 版本 2.0.0 源码地址:https://gitee.com/pearl-organization/study-seata-demo 文章目录 1. 背景2. 简介3. 适用人群4. 环境及版本5. 文章导航5…...
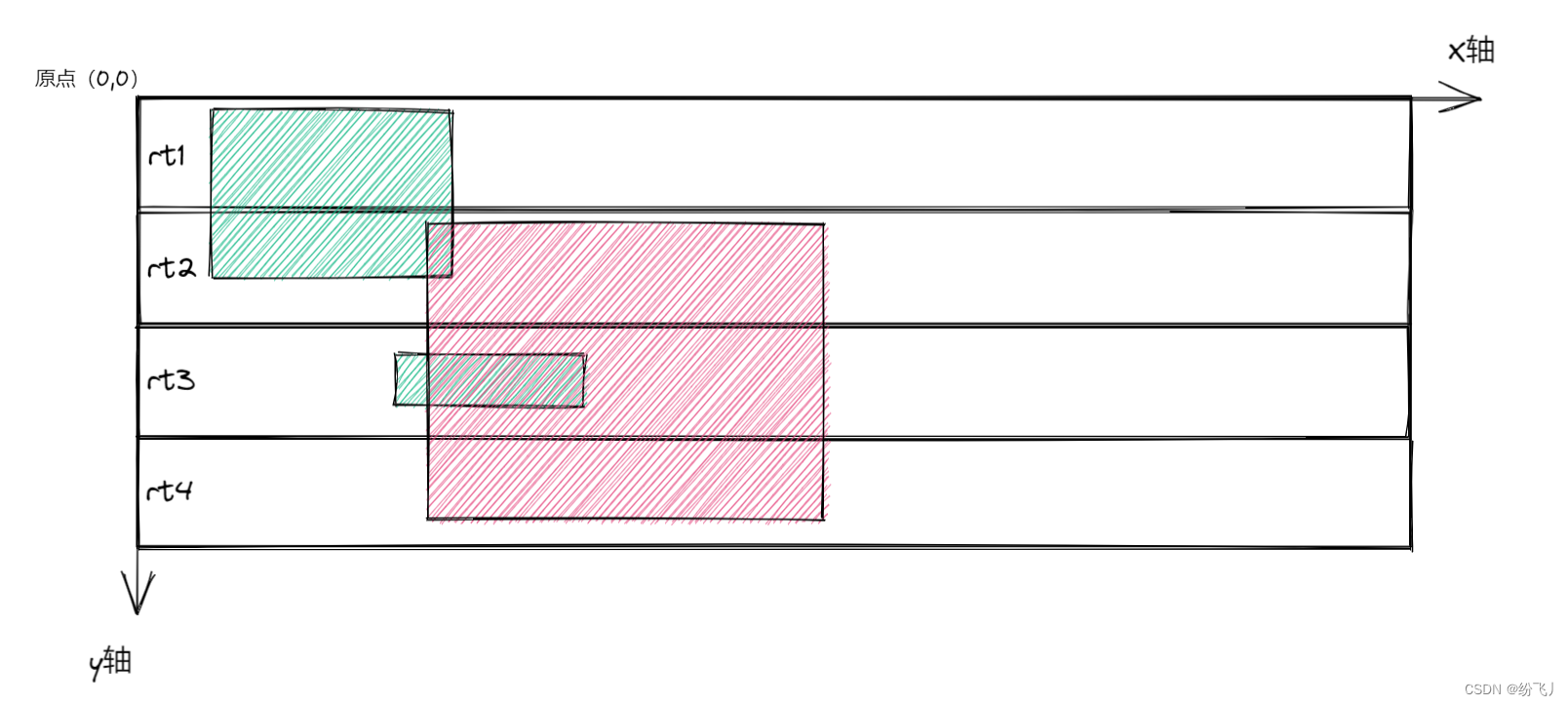
fly-barrage 前端弹幕库(3):滚动弹幕的设计与实现
项目官网地址:https://fly-barrage.netlify.app/; 👑🐋🎉如果感觉项目还不错的话,还请点下 star 🌟🌟🌟。 Gitee:https://gitee.com/fei_fei27/fly-barrage&a…...
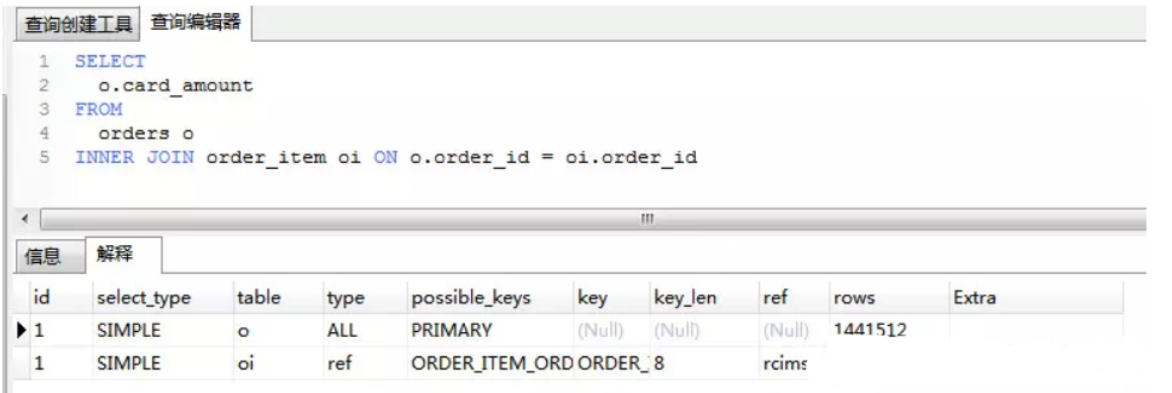
Mysql面试总结
基础 1. 数据库的三范式是什么? 第一范式:强调的是列的原子性,即数据库表的每一列都是不可分割的原子数据项。第二范式:要求实体的属性完全依赖于主关键字。所谓完全 依赖是指不能存在仅依赖主关键字一部分的属性。第三范式&…...

【深圳五兴科技】Java后端面经
本文目录 写在前面试题总览1、java集合2、创建线程的方式3、对spring的理解4、Spring Boot 和传统 Spring 框架的一些区别5、springboot如何解决循环依赖6、对mybatis的理解7、缓存三兄弟8、接口响应慢的处理思路9、http的状态码 写在前面 关于这个专栏: 本专栏记录…...
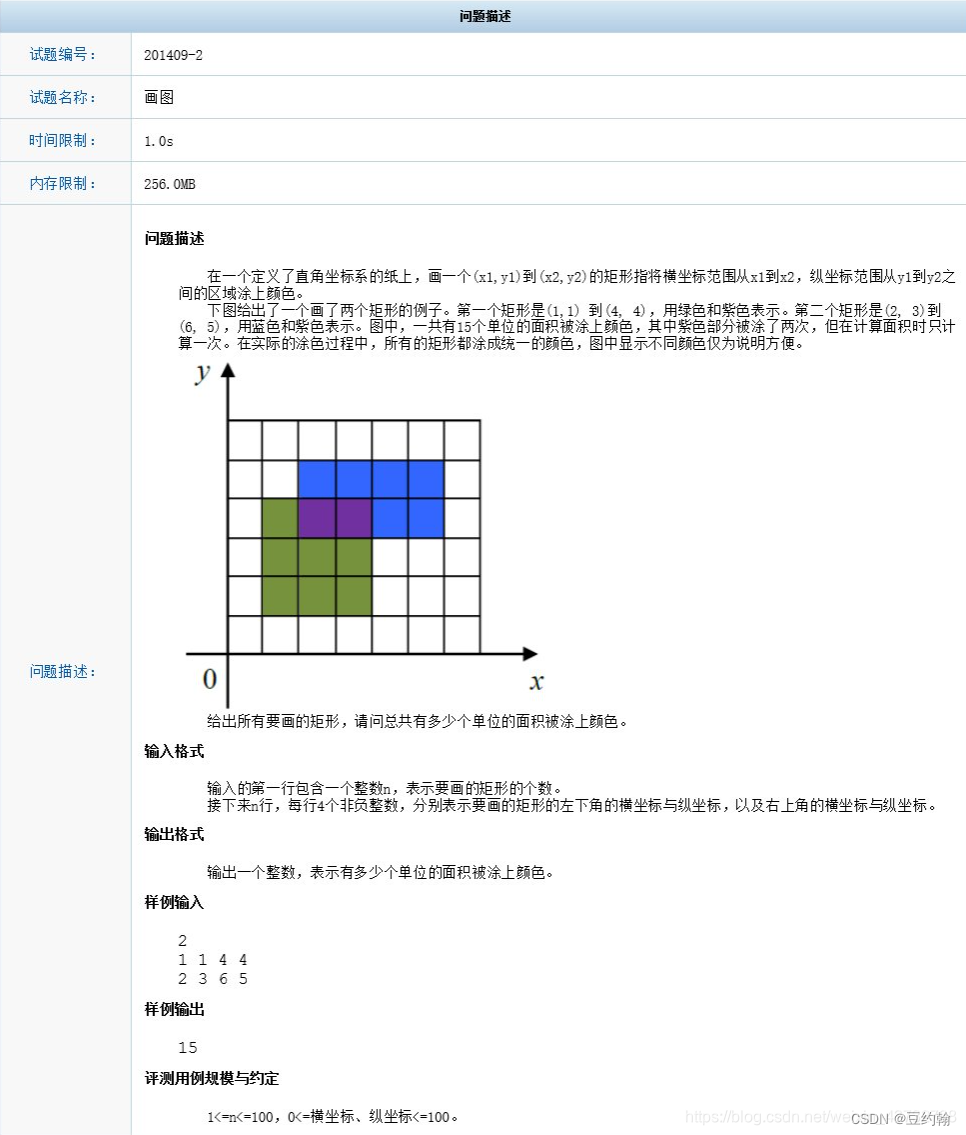
画图(ccf201409-2)解题思路
解题思路 填充100*100二维数组,范围内的元素修改成1,最后累积求和。...
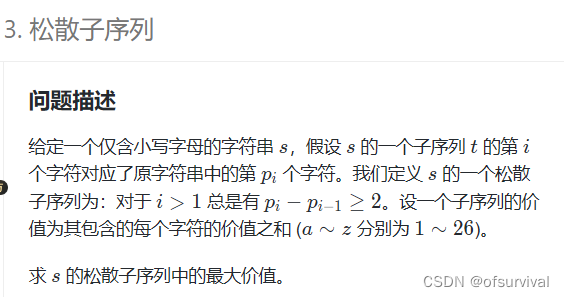
蓝桥杯刷题(一)
一、 import os import sys def dps(s):dp [0] * len(s)dp[0] ord(s[0]) - 96if len(s) 1:return dp[-1]dp[1] max(ord(s[0]) - 96, ord(s[1]) - 96)for i in range(2, len(s)):dp[i] max(dp[i - 1], dp[i - 2] (ord(s[i])) - 96)return dp[-1] s input() print(dps(s))…...

设计模式:策略模式 ⑥
一、策略模式思想 简介 策略模式(Strategy Pattern)属于对象的行为模式。其用意是针对一组算法,将每一个算法封装到具有共同接口的独立的类中,从而使得它们可以相互替换。策略模式使得算法可以在不影响到客户端的情况下发生变化。…...

数据结构从入门到精通——顺序表
顺序表 前言一、线性表二、顺序表2.1概念及结构2.2 接口实现2.3 数组相关面试题2.4 顺序表的问题及思考 三、顺序表具体实现代码顺序表的初始化顺序表的销毁顺序表的打印顺序表的增容顺序表的头部/尾部插入顺序表的头部/尾部删除指定位置之前插入数据和删除指定位置数据顺序表元…...

001-CSS-水平垂直居中布局
水平垂直居中布局 方案一:弹性盒子布局方案二:绝对定位 transform方案三:margin 绝对定位,四个方向为零方案四:绝对定位 margin方案五:绝对定位 calc 方案一:弹性盒子布局 💡 T…...
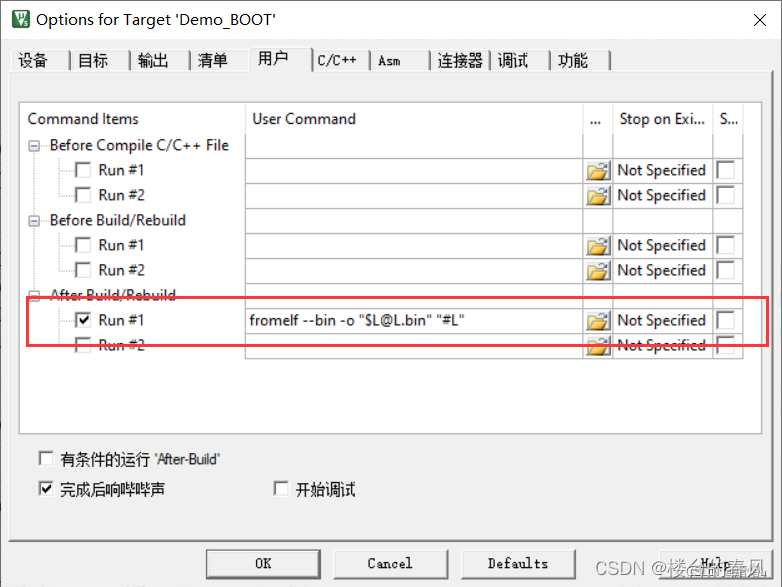
【[STM32]标准库-自定义BootLoader】
[STM32]标准库-自定义BootLoader BootloaderBootloader的实现BOOTloader工程APP工程 Bootloader bootloader其实就是一段启动程序,它在芯片启动的时候最先被执行,可以用来做一些硬件的初始化或者用作固件热更新,当初始化完成之后跳转到对应的…...
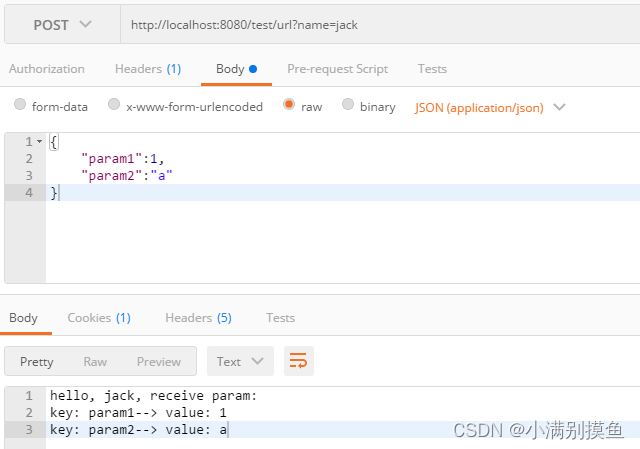
Spring Boot项目中不使用@RequestMapping相关注解,如何动态发布自定义URL路径
一、前言 在Spring Boot项目开发过程中,对于接口API发布URL访问路径,一般都是在类上标识RestController或者Controller注解,然后在方法上标识RequestMapping相关注解,比如:PostMapping、GetMapping注解,通…...

Vue中有哪些优化性能的方法?
Vue是一款流行的JavaScript框架,用于构建交互性强的Web应用程序。在前端开发中,性能优化是一个至关重要的方面,尤其是当应用程序规模变大时。Vue提供了许多优化性能的方法,可以帮助开发人员提升应用程序的性能,从而提升…...

Python pandas遍历行数据的2种方法
背景 pandas在数据处理过程中,除了对整列字段进行处理之外,有时还需求对每一行进行遍历,来处理每行的数据。本篇文章介绍 2 种方法,来遍历pandas 的行数据 小编环境 import sysprint(python 版本:,sys.version.spli…...

Spring之@Transactional源码解析
前言 我们在日常开发的时候经常会用到组合注解,比如:EnableTransactionManagement Transactional、EnableAsync Async、EnableAspectJAutoProxy Aspect。今天我们就来抽丝剥茧,揭开Transactional注解的神秘面纱 EnableTransactionManagement注解的作用 当我们看到类似Ena…...

第三届国际亲子游泳学术峰会,麒小佑为亲游行业提供健康解决方案
第三届国际亲子游泳学术峰会大合影 2024年2月26—28日,第三届国际亲子游泳学术峰会在中国青岛成功召开。 第三届国际亲子游泳学术峰会是中国婴幼游泳行业最高标准的学术性会议,由亲游圈主办,旨在为本行业搭建一个高端圈层,帮助机…...

Python光速入门 - Flask轻量级框架
FlASK是一个轻量级的WSGI Web应用程序框架,Flask的核心包括Werkzeug工具箱和Jinja2模板引擎,它没有默认使用的数据库或窗体验证工具,这意味着用户可以根据自己的需求选择不同的数据库和验证工具。Flask的设计理念是保持核心简单,…...

C/C++ 说说引用这玩仍是干啥的
引用的本质就是给某个实例对象起个外号。生活中李逵,也叫黑旋风。诸葛亮,又叫孔明。 引用的方式: 类型& 引用名对象名 举个例子 int i0; int& ki;//这种方式就是引用----->i有了自己的小名,从次叫k了 std::cout<…...
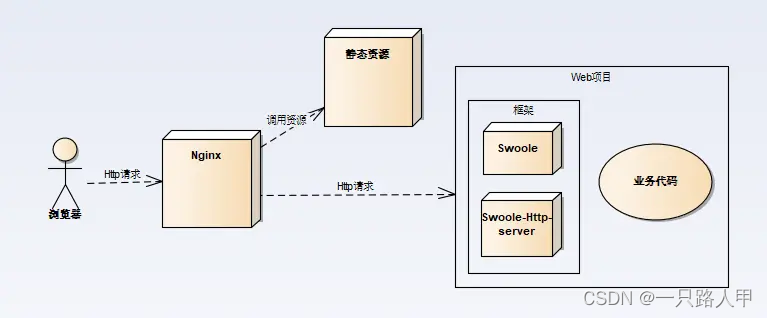
swoole
php是单线程。php是靠多进程来处理任务,任何后端语言都可以采用多进程处理方式。如我们常用的php-fpm进程管理器。线程与协程,大小的关系是进程>线程>协程,而我们所说的swoole让php实现了多线程,其实在这里来说,就是好比让php创建了多个进程,每个进程执行一条…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...
