leetcode470 用Rand7()实现Rand10()
力扣470
第一步:根据Rand7()函数制作一个可以随机等概率生成0和1的函数rand_0and1
调用Rand7()函数,随机等概率生成1,2,3,4,5,6,7
这时我们设置:生成1,2,3(也就是小于4)的时候,我们的rand_0and1函数就返回0
生成4,5,6(也就是小于4)的时候,我们的rand_0and1函数就返回1
如果生成7,那我们继续再调用一次Rand7()函数
public int rand_0and1(){ int temp=rand7();int result=0;if(temp<4){result=0;}else if(result>=4&&result<7){result=1;}else//temp=7{while(temp!=7){temp=rand7();}//跳出循环说明终于得到一个不为7的随机数,1,2,3,4,5,6其中之一result=temp<4?0:1;}reurn result;}第二步:要生成的是1~10,我们先生成0~9(然后加1即可),怎么由我们第一步得到的0~1生成0~9呢?
1个二进制位可以保证等概率返回0,1
2个二进制位可以保证等概率返回0,1,2,3
3个二进制位可以保证等概率返回0,1,2,3,4,5,6,7
4个二进制位就可以保证等概率返回(最小是0000,最大是1111十五)0,1,2,3,4,5,6,7.......15
当发现返回的大于9,那就重新生成一个新的数,直到生成一个0~9之间的数
记rand_0and1()产生的值为temp

class Solution extends SolBase
{public int rand10(){int result=0;result=(rand_0and1())+(rand_0and1()<<1)+(rand_0and1()<<2)+(rand_0and1()<<3);if(result<10){return result+1;}else{while(result>=10){result=(rand_0and1())+(rand_0and1()<<1)+(rand_0and1()<<2)+(rand_0and1()<<3);}//跳出循环,说明终于生成了一个比10小的数,符合要求return result+1;}}public int rand_0and1(){int result=0;result=rand7();if(result<4){return 0;}else if(result>=4&&result<7){return 1;}else//result=7{while(result==7){result=rand7();}//跳出循环说明终于得到一个不为7的随机数return result<4?0:1;}}
}通过rand5()生成rand7()也是一样的,
第一步:先通过rand5()函数制作一个可以随机等概率生成0和1的函数rand_0and1(生成1,2就返回0,生成3,4就返回1,生成5就重新再生成1个数,直到生成不等于5的数返回0或者1)
第二步:通过rand_0and1随机等概率生成0~6
result=(rand_0and1())+(rand_0and1()<<1)+(rand_0and1()<<2);
生成大于6的数,就重新生成,直到生成一个小于等于6的数
相关文章:

leetcode470 用Rand7()实现Rand10()
力扣470 第一步:根据Rand7()函数制作一个可以随机等概率生成0和1的函数rand_0and1 调用Rand7()函数,随机等概率生成1,2,3,4,5,6,7 这时我们设置:生成1,2&a…...

JSON数据解析商品详情API
大家有探讨稳定获取商品主图、jiage、标题,及sku的完整解决方案。这个引起了我技术挑战的兴趣,然后各种网上资料查询,最终还是不负努力,找到更好的解决方案,不再出现任何滑块验证码,完全绕过,实…...

服务端开发Java面试复盘篇1
上周投了一些简历,约了8-9家面试,其中完成了3家的第一轮面试,由于面试的是Java 的实习生,感觉问的题目都比较基础,不过有些问题回答的不是很好,在这里对回答的不太好的题目做一下总结和复盘。 目录 一、后…...

Android框架WiFi架构
同学,别退出呀,我可是全网最牛逼的 WIFI/BT/GPS/NFC分析博主,我写了上百篇文章,请点击下面了解本专栏,进入本博主主页看看再走呗,一定不会让你后悔的,记得一定要去看主页置顶文章哦。 一、wpa_supplicant:wpa_supplicant本身开源项目源码,被谷歌收购之后加入Android移…...

rt-thread 移植调试记录
rt-thread 移植调试记录 记录rt-thread移植的过程。这里移植仅仅是利用rt-thread源码目录已经移植好的文件,组建自己的工程,不需要自己编写汇编完成底层移植。 1. 搭建基础工程 这里使用的是正点原子的潘多拉开发板,MCU为stm32l475。需要先…...

红外线额温枪与红外线温度传感器的原理分析
额温枪主要针对测量人体额温基准而设计,使用也非常简单方便。测体温可以达到一秒即可准确测量。并且不需要接触人体,隔着空气即可一键测温。非常适合家庭、学校、企业等场所。 但是由于其精度原因(一般为 0.2 ℃,也有更低的&#…...

2023牛客寒假算法集训营4
目录A. [清楚姐姐学信息论](https://ac.nowcoder.com/acm/contest/46812/A)(数学)B. [清楚姐姐学构造](https://ac.nowcoder.com/acm/contest/46812/B)(数学 构造)C. [清楚姐姐学01背包(Easy Version)](https://ac.nowcoder.com/…...
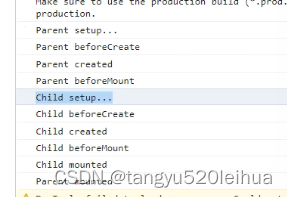
vue组合式API及生命周期钩子函数
一、组合式API 什么是组合式API? vue3中支持vue2的选项式、支持新的编程模式–函数式编程(没有this指针)做了一个兼容,可以在一个组件中使用函数式编程和OOP编程(选项式) setup()函数 可以使用setup属性…...

Python|每日一练|数组|回溯|二分查找|排序和顺序统计量|.update方法 |单选记录:组合总和|寻找峰值|编程通过键盘输入每一位运动员
1、组合总和(数组、回溯) 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的数字可以无限制重复被选取。 说明: 所有数字(包括 t…...
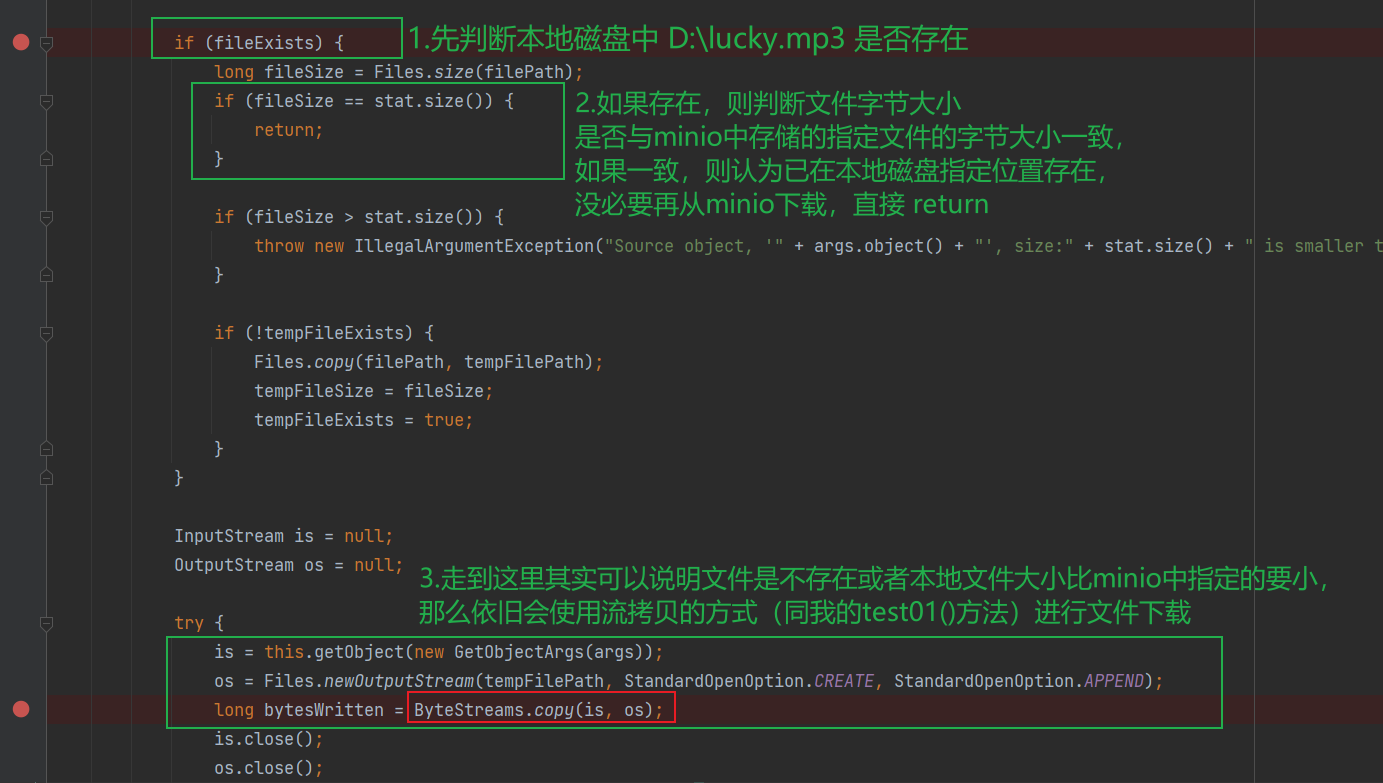
minio下载文件速度很慢的原因分析与说明
文章目录1.实战背景2.问题描述3.问题分析4.问题解决1.实战背景 最近在做一个项目,需要用到minio来搭建文件系统,先简单说一下我在项目中设置的上传文件流程: 前端将分块文件逐一传给后端,后端再存储到 linux服务器的minio 当中。…...

基于comsol软件弯曲单模光纤模拟仿真
在本节中,主要基于实验室实际光纤单模圆柱光纤进行模拟,与comsol案例库文件在分析过程和建模有些差异: 模拟主要通过以下三个步骤进行:模型的几何构建、物理场的添加研究、结构处理分析来进行。 下面是第一步骤:几何…...

如何开启多个独立Chrome浏览器
一、简介 作为测试或者开发人员,有些情况下会用到 Chrome 浏览器,但有时是同一个 Chrome 浏览器无法为我们提供隔离开的不同环境。这样 我们就需要清理 cache 、切换账号等,降低了我们的工作效率。今天的主题是如何开启多个独立的 Chrome 浏…...

erp5开源制造业erp主要业务会计分录处理
erp5开源制造业erp主要业务会计分录处理 采购业务的会计分录 收到发票时 借:材料采购 (1201) 应交税费-应交增值税(进项税)(21710101) 贷:应付账款 (2121) 付款时 借:应付账款 (2121) 贷:银行存款 (1002) 入…...
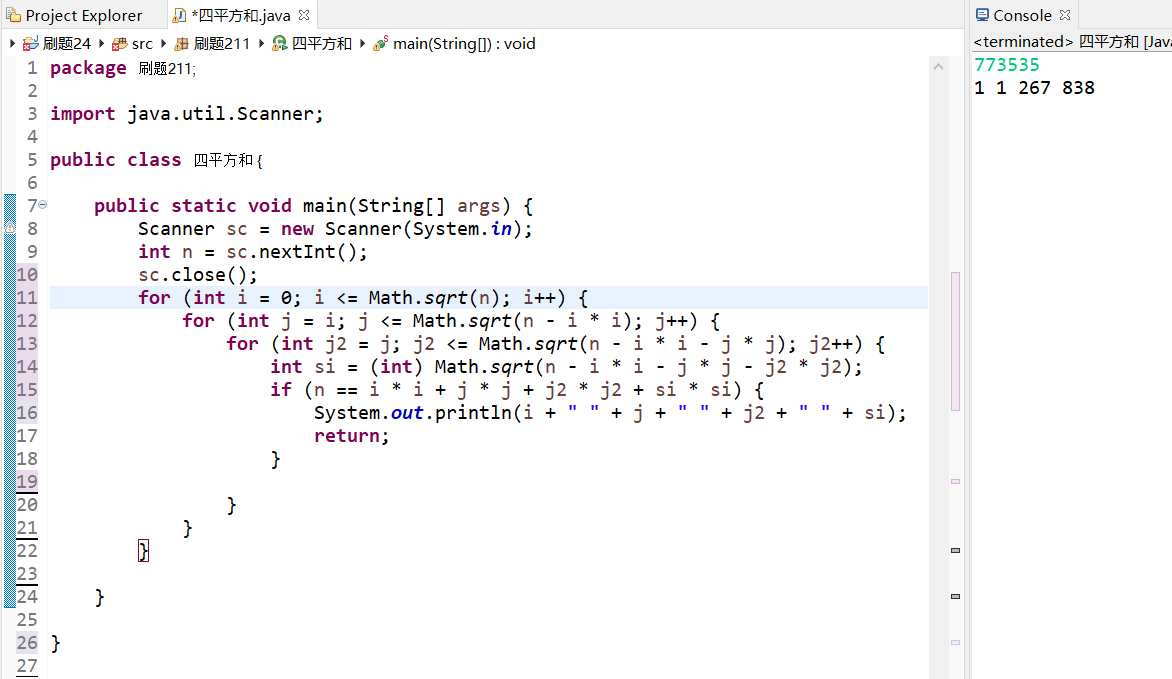
技能树基础——17四平方和(拉格朗日定理,嵌套循环)
题目:四平方和定理,又称为拉格朗日定理:每个正整数都可以表示为至多4个正整数的平方和。如果把0包括进去,就正好可以表示为4个数的平方和。比如:5 0^ 2 0^ 2 1^ 2 2^27 1^ 2 1^ 2 1^ 2 2^2 (^符号表…...

JPA、EJB、事物管理---相关内容整理
目录 ■前言 ■实现原理:容器管理事务 ■代码实现简单描述: 1.JPA ■定义 ■1.1.配置文件 ■1.2.OSS jar ■1.3.一些OPA的类(举例) ■1.4. jpa 框架在实体类(Entity)中添加非数据库字段的属性--…...
C语言学习笔记(一):了解C语言
什么是C语言 C语言是一种高级编程语言,最早由丹尼斯里奇在1972年开发。它是一种通用编程语言,提供了高级编程语言的方便和易用性,同时又有较低级别的编程语言的灵活性和效率。C语言在许多操作系统、编译器和应用程序开发中广泛使用ÿ…...

回头看——《智能家居项目小结》
openAI兴起,于是拿着之前小组合作的项目(承认优化较差),交给AI试着帮忙优化下1.功能函数(TCP_SER_INIT)优化源代码:int TCP_SER_INIT(int *tcpsocket, const char *ip, const char *…...
社交登陆OAuth2.0
QQ、微博、github 等网站的用户量非常大,别的网站为了 简化自我网站的登陆与注册逻辑,引入社交登陆功能; 步骤: 1)、用户点击 QQ 按钮 2)、引导跳转到 QQ 授权页 3)、用户主动点击授权ÿ…...
C++005-C++选择与分支2
文章目录C005-C选择与分支2条件语句C实现else if 语句题目描述 根据成绩输出成绩等级ABCDEif嵌套语句题目描述 输出三个数中的最大值题目描述 模拟游戏登录switch语句三元运算符题目描述 输出三个数中的最大值-基于3元运算符题目描述 根据1-7输出星期1-星期日案例练习题目描述 …...

IPFS 简介及概述
文章目录 IPFS 简介IPFS 包含的协议内容及其理解IPFS 和 BitTorrent 区别IPFS 简介 星际文件系统(InterPlanetary File System). IPFS 是一个分布式的网络文件系统, 点到点超媒体协议. 可以让我们的互联网速度更快, 更加安全, 并且更加开放. IPFS协议的目标是取代传统的互联网…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
