49.在ROS中实现local planner(2)- 实现Purepersuit(纯跟踪)算法
48.在ROS中实现local planner(1)- 实现一个可以用的模板实现了一个模板,接下来我们将实现一个简单的纯跟踪控制,也就是沿着固定的路径运动,全局规划已经规划出路径点,基于该路径输出相应的控制速度
1. Pure Pursuit
Pure Pursuit路径跟随便是基于受约束移动机器人圆周运动的特性所开发出来的运动控制方式。原理十分简单,如图所示,移动机器人有一个前视的搜索半径,与机器人规划的路径有一个焦点,假设机器人从当前位置到路径焦点的运动为圆周运动。其中的前视距离便是图1中的L。根据几何关系便可以计算机器人的运动半径。

受约束的机器人模型(不能横向运动)可由两个控制量组成,即运动参考点的线速度v与角速度w。在极短的运行周期中,机器人都是以固定的线速度与角速度运动。因此机器人的运动可以视为圆周运动(w=0时为直线运动)。
2. 运动半径推算
如图所示的机器人便是绕着一个旋转中心进行圆周运动,于是移动机器人的运动控制可视为求解其在运动过程中的实时旋转半径。图中,r为移动机器人的旋转半径。
我们以base坐标系为例,及当前机器人为坐标原点,x轴为前方,y轴为左方,即ROS的坐标系,(x,y)为目标点, L为距离目标点的距离(前视距离),如下计算,容易求得旋转半径r
由图可得d=r−yd = {r - y} d=r−y
d2+x2=r2d^2+x^2 = r^2 d2+x2=r2
即:r2−2ry+y2+x2=r2r^2-2ry+y^2+x^2 = r^2 r2−2ry+y2+x2=r2
即:x2+y2=2ryx^2+y^2 = 2ry x2+y2=2ry
即:L2=2ryL^2 = 2ry L2=2ry
即:r=L2/2yr = L^2/2y r=L2/2y
即运动半径=前视距离的平方/两倍的y
我们知道r=v/w 即我们只需要给定v/w为固定的值即可
因v与L相关 我们取一次关系
令v=aL a为长数项
可得w=v/r=a*2y/L
3. 坐标转换
我们知道setPlan下发的坐标一般使用的是map坐标系,我们计算的时候需要转换为base坐标系
我们可以使用init接口提供的tf::TransformListener即可完成, (1.14.0版本后接口更新,使用新的接口)
geometry_msgs::PoseStamped PurepursuitPlanner::goalToBaseFrame(const geometry_msgs::PoseStamped& goal_pose_msg) {#if ROS_VERSION_GE(ROS_VERSION_MAJOR, ROS_VERSION_MINOR, ROS_VERSION_PATCH, 1, 14, 0)geometry_msgs::PoseStamped goal_pose, base_pose_msg;goal_pose = goal_pose_msg;goal_pose.header.stamp = ros::Time(0.0);try {base_pose_msg = tf_->transform(goal_pose, "base_link");} catch (tf2::TransformException& ex) {ROS_WARN("transform err");return base_pose_msg;}#elsegeometry_msgs::PoseStamped base_pose_msg;tf::Stamped<tf::Pose> goal_pose, base_pose;poseStampedMsgToTF(goal_pose_msg, goal_pose);goal_pose.stamp_ = ros::Time();try {tf_->transformPose(costmap_ros_->getBaseFrameID(), goal_pose, base_pose);} catch (tf::TransformException& ex) {ROS_WARN("transform err");return base_pose_msg;}tf::poseStampedTFToMsg(base_pose, base_pose_msg);#endifreturn base_pose_msg;}4. 前视距离
我们不断根据当前位置,更新前视距离,通过前面的接算,给定速度
4.1 前视距离大小设置
前世距离可以根据V我们预设速度相关
-
如果前世距离较大,相当于路径采样间隔较大,跟踪路径与规划路径的偏差会大。
-
如果前世距离较小,机器人容易抖动
4.2 前视距离更新策略
如果当前距离路径中前视距离的点后的n个点的距离小于前世距离,则更新前视距离
即如果当前前视距离的点在路径索引为n,则判断n+m索引距离当前点位置是否小于预设前视距离值
5. 速度限制
一般机器人小车,线速度是>0的即,只能前进,无法后退。这就需要我们新增当前前视点角度判断, 如果角度超过90,即在车的后方。可以对速度修正强制旋转
auto target_yaw_diff = atan2(goal.pose.position.y, goal.pose.position.x); // 当前目标点相对机器人的角度.... // 计算半径 速度// 当前目标点相对机器人的角度 相差较大(即目标点在机器人后面), 需要直发角速度(即原地旋转), 转向目标点if (target_yaw_diff > PI*0.5) {cmd_vel.linear.x = 0;cmd_vel.angular.z = 0.8;} else if (target_yaw_diff < -PI*0.5) {cmd_vel.linear.x = 0;cmd_vel.angular.z = -0.8;}
6. 完成判断
我们在前视点到达规划路径的最后一个时,且当前点与该最后一点距离差小于预设的容忍差,强制输出0速度
if (got && l < GOAL_TOERANCE_XY) {goal_reached_ = true;cmd_vel.angular.z = 0;cmd_vel.linear.x = 0;}
7. 测试
- 修改
move_base配置文件move_base_params.yaml
# base_local_planner: "dwa_local_planner/DWAPlannerROS"
base_local_planner: pure_pursuit_local_planner/PurepursuitPlanner
dwa_local_planner/DWAPlannerROS—>pure_pursuit_local_planner/PurepursuitPlanner
- 启动模拟器
pibot_simulator
- 启动rviz
pibot_view

相关文章:

49.在ROS中实现local planner(2)- 实现Purepersuit(纯跟踪)算法
48.在ROS中实现local planner(1)- 实现一个可以用的模板实现了一个模板,接下来我们将实现一个简单的纯跟踪控制,也就是沿着固定的路径运动,全局规划已经规划出路径点,基于该路径输出相应的控制速度 1. Pur…...
Allegro如何设通孔Pin和Via的消盘操作指导
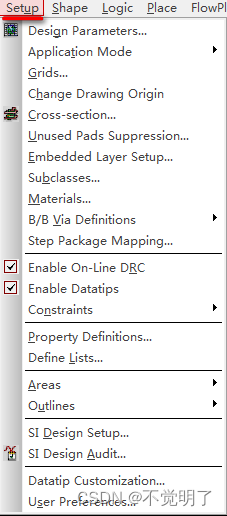
Allegro如何设通孔Pin和Via的消盘操作指导 用Allegro做PCB设计的时候,除了可以在光绘设置里面设置内层通孔Pin和Via的消盘,在设计过程中,同样也可以设置消盘效果,以便实时显示,如下图 如何设置,具体操作如下 点击Setup点击Unused Pads Suppression...
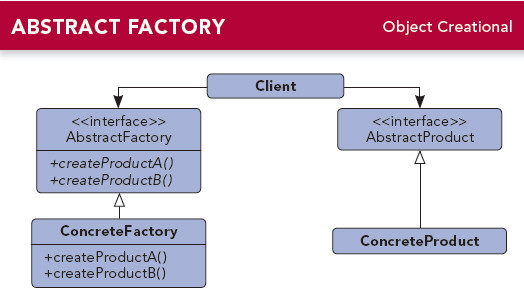
Android工厂模式
工厂模式分为三种 :简单工厂模式 、工厂方法模式 、抽象工厂模式 。 目录 简单工厂模式 UML图 实现 使用场景: 优点 : 缺点: 工厂方法模式 UML图 实现 使用场景: 优点: 缺点: 抽象工厂模式 UM…...

神经网络硬件加速器-架构篇
架构设计 常规架构通常包括两种: 1、全流水线架构,顾名思义,将整个神经网络进行平铺,并对每一层进行优化设计,优点:实现高吞吐率和低延时。缺点:消耗大量硬件资源,通常无法跨网络或…...
)
Python raise用法(超级详细,看了无师自通)
是否可以在程序的指定位置手动抛出一个异常?答案是肯定的,Python 允许我们在程序中手动设置异常,使用 raise 语句即可。 大家可能会感到疑惑,即我们从来都是想方设法地让程序正常运行,为什么还要手动设置异常呢&#…...
1.SpringSecurity快速入门
*SpringScurity的核心功能: 认证:验证当前访问系统的是不是本系统的用户,并且要确认具体是哪个用户 授权:经过认证后判断当前用户是否有权限进行某个操作 *第一步:创建springboot工程 *第二步:引入SpringSecurity依赖 *第三步:写controller,访问对应的url:localhos…...
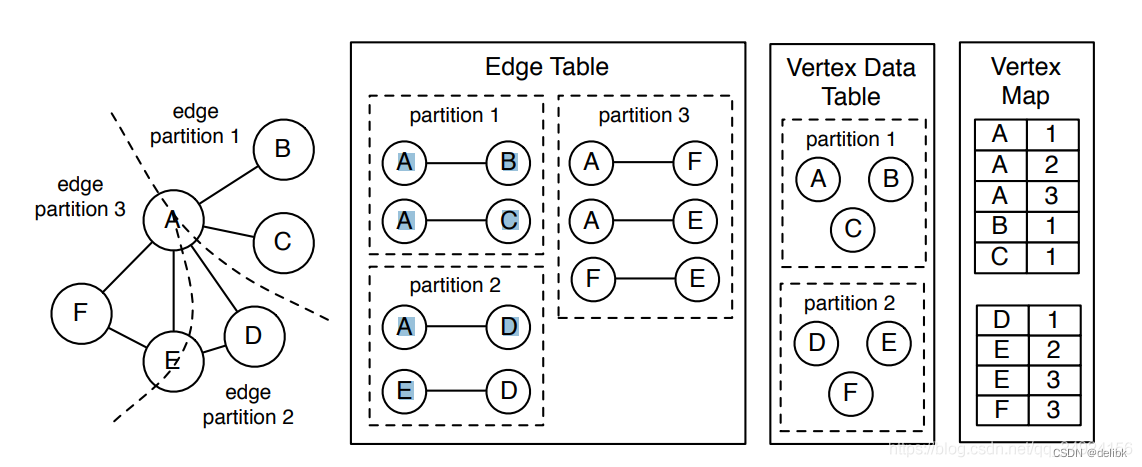
Graph Partition: Edge cut and Vertex cut
Graph PartitionEdge cut and Vertex cutEdge cutVertex cut实际如何进行点分割和边分割的呢?Graph store format情况1:按照边列表存储:情况2:按照邻接表存储:Edge cut and Vertex cut 图结构描述了数据流动ÿ…...

Javascript周学习小结(初识,变量,数据类型)
JS的三大书写方式行内式如图所示:几点说明:JS的行内式写在HTML的标签内部,(常以on开头),如onclick行内式常常使用单引号括住字符串以区分HTML的双引号可读性差,不建议使用引号易出错,不建议使用特殊情况下使…...
C语言-基础了解-10-C函数
C函数 一、C函数 函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() ,所有简单的程序都可以定义其他额外的函数。 您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定的,但在逻辑上&…...
【LeetCode】剑指 Offer(16)
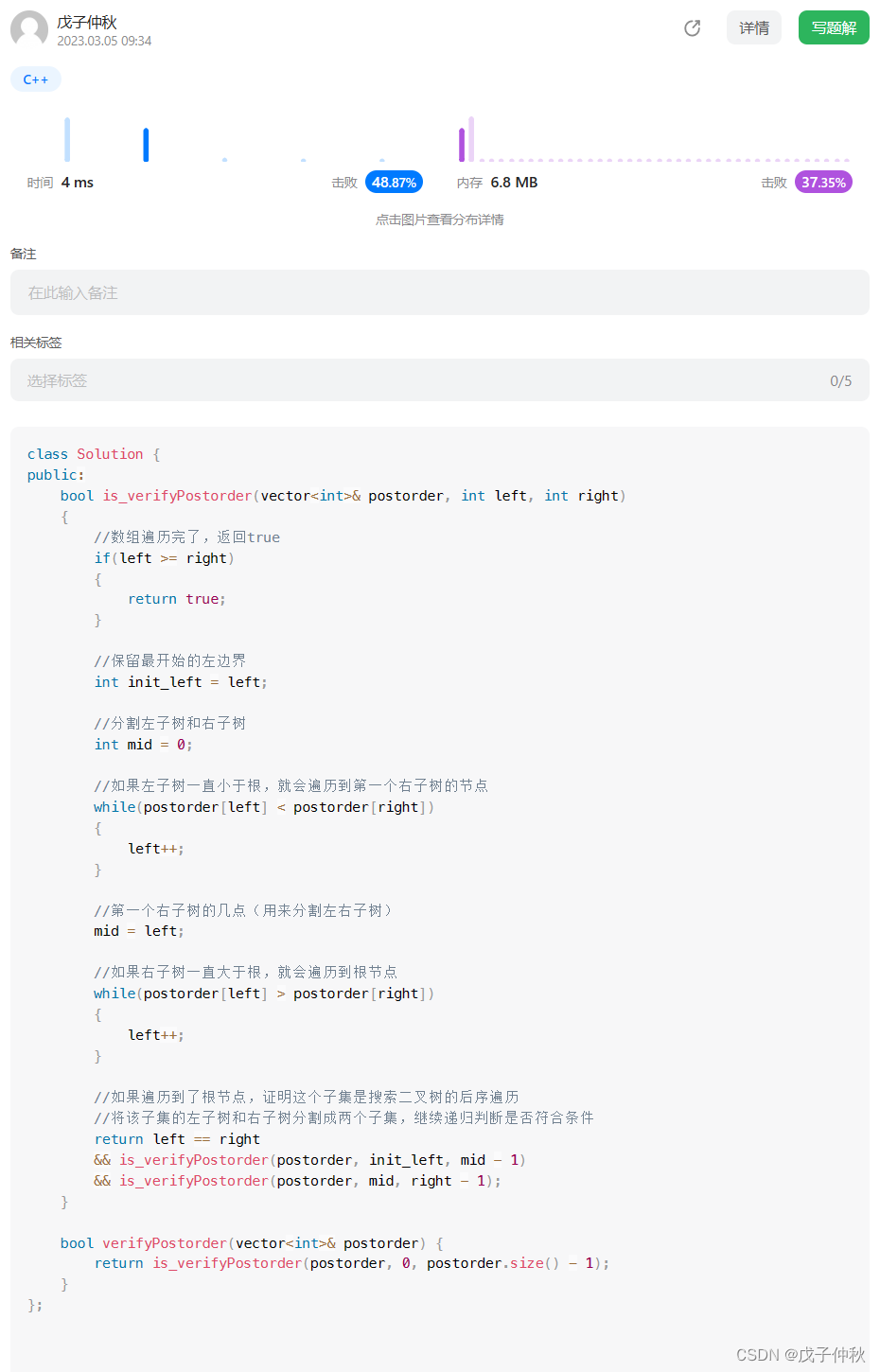
目录 题目:剑指 Offer 33. 二叉搜索树的后序遍历序列 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer …...
)
第三十九章 linux-并发解决方法二(互斥锁mutex)
第三十九章 linux-并发解决方法二(互斥锁mutex) 文章目录第三十九章 linux-并发解决方法二(互斥锁mutex)互斥锁的定义与初始化互斥锁的DOWN操作互斥锁的UP操作用count1的信号量实现的互斥方法还不是Linux下经典的用法,…...

脚本方式本地仓库jar包批量导入maven私服
脚本内容,将以下内容保存为mavenimport.sh,放置于需要上传的目录下,可以是顶层目录,或者某个分包的目录,若私服已有待上传的包,则执行会被替换 #!/bin/bash # copy and run this script to the root of th…...

【c++】引用的学习
引用的定义和声明 引用是一种别名,它允许使用与原变量相同的内存位置。在C中,引用是使用&符号来定义的。引用必须在定义时初始化,并且可以与原变量分别使用。 int a 10; int& b a; // 定义了一个引用b,它指向a引用的作用…...

linux 软件安装及卸载
1.联网在线安装及卸载ubuntu环境下:使用apt-get 工具apt-get install - 安装软件包apt-get remove - 移除(卸载)软件包CentOS环境下:使用yum工具 (银河麒麟系统属于centos)yum install - 安装软件包yum rem…...
XShell连接ubuntu20.04.LTS
1 下载XshellXShell官方下载地址打开XSHELL官方下载地址,我们可以选择【家庭和学校用户的免费许可证】,输入邮箱之后即可获得下载链接安装非常简单,跟着提示进行即可。2 连接ubuntu2.1 查看ubuntu的ip地址输入命令查看ip地址ifconfig刚开始可…...

【FPGA】Verilog:MSI/LSI 组合电路之解码器 | 多路分解器
写在前面:本章将理解编码器与解码器、多路复用器与多路分解器的概念,通过使用 Verilog 实现多样的解码器与多路分解器,通过 FPGA 并使用 Verilog 实现。 Ⅰ. 前置知识 0x00 解码器与编码器(Decoder / Encoder) 解码器…...

深入理解JDK动态代理原理,使用javassist动手写一个动态代理框架
文章目录一、动手实现一个动态代理框架1、初识javassist2、使用javassist实现一个动态代理框架二、JDK动态代理1、编码实现2、基本原理(1)getProxyClass0方法(2)总结写在后面一、动手实现一个动态代理框架 1、初识javassist Jav…...
一、策略模式的使用
1、策略模式定义: 策略模式(Strategy Pattern)定义了一组策略,分别在不同类中封装起来,每种策略都可以根据当前场景相互替换,从而使策略的变化可以独立于操作者。比如我们要去某个地方,会根据距…...

Verilog使用always块实现时序逻辑
这篇文章将讨论 verilog 中一个重要的结构---- always 块(always block)。verilog 中可以实现的数字电路主要分为两类----组合逻辑电路和时序逻辑电路。与组合逻辑电路相反,时序电路电路使用时钟并一定需要触发器等存储元件。因此,…...
面向对象设计模式:行为型模式之迭代器模式
一、迭代器模式,Iterator Pattern aka:Cursor Pattern 1.1 Intent 意图 Provide a way to access the elements of an aggregate object sequentially without exposing its underlying representation. 提供一种按顺序访问聚合对象的元素而不公开其基…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
