当前位置： 首页 > news >正文

德鲁特金属导电理论（Drude）

news 2026/2/7 19:36:33

德鲁特模型的重要等式

首先我们建立德鲁特模型的重要等式

\vec F_e =m_e \frac{d\vec v}{dt}=-e\vec E-m_e\frac{\vec v}{\tau}

我们把原子对于电子的阻碍作用，用一个冲量近似表示出来

在式子\frac{d\vec v}{dt}=-\frac{e \vec E}{m_e}-\frac{\vec v}{ \tau}

首先定义一个等效加速度

\frac{e\vec E}{m_e}=\frac{\vec v_d}{\tau}

由于

\vec j=-ne\vec v=-ne\vec v_d=ne(\frac{e\vec E \tau}{m_e})=\sigma_0 \vec E 

我们可以得到电导率的微观表达式\sigma_0 =\frac{ne^2 \tau } { m_e }

在交流电环境中

电场的表达式E(t)=E(\omega)e^{i\omega t}

 借鉴上一问的公式

我们可以列出这样的表达式

m\frac{d\vec v(t)}{dt}=-eE(t)-m_e \frac{\vec v(t)}{\tau}，代入电场的表达式，我们可以得到

m\frac{E(\omega) de^{-i\omega t}}{dt}=-eE(\omega) de^{-i\omega t}-m_e \frac{\vec v(\omega)e^{-i\omega t}}{\tau}

左边求导数，我们可以得到

-i\omega m_e E(\omega) e^{-i\omega t}=-eE(\omega) de^{-i\omega t}-m_e \frac{\vec v(\omega)e^{-i\omega t}}{\tau}

化简可以得到

m_e \vec v(\omega)e^{-i\omega t}(-i\omega +\frac{1}{\tau})=-e\vec E e^{-i\omega t}

我们解得

m_e \vec v(\omega)=-\frac{e\vec E(\omega)}{(\frac{1}{\tau}-i\omega)}

\vec v(\omega)=-\frac{e\vec E(\omega)}{m_e (\frac{1}{\tau}-i\omega)}

解得

\vec j=-ne\vec v= \frac{ne^{2} }{m_e (\frac{1}{\tau}-i\omega)}\vec E(\omega)

我们可以得到

\sigma(\omega)=\frac{ne^{2} }{m_e (\frac{1}{\tau}-i\omega)}

这个式子的重要应用就是EM波，电磁波在金属中的传播

\sigma(\omega)=\frac{ne^{2} }{m_e (\frac{1}{\tau}-i\omega)}=\frac{\sigma_0}{(1-i\omega \tau)}

在电磁波的传播中要记住这么几个等式

首先是色散关系表达式

k^2=\frac{\omega^2}{c^2}\varepsilon(\omega),\varepsilon(\omega)=1+\frac{i\sigma_0}{\varepsilon_0 \omega(1-i\omega \tau)}

我们定义plasma frequency

\omega_p=\sqrt{\frac{n e^2}{ m_e \varepsilon_0}}

我们可以得到

\varepsilon(\omega)=1+\frac{\omega_p^{2}}{\omega(\frac{1}{i\tau}-\omega)}

\varepsilon(\omega)=1-\frac{\omega_p^{2}}{i\frac{\omega}{\tau}+\omega^2}

if \ \ \ \omega \tau>>1,\omega^2>>\frac{\omega}{\tau}

\varepsilon(\omega)=1-\frac{\omega_p^{2}}{i\frac{\omega}{\tau}+\omega^2}=1-\frac{\omega_p^2}{\omega^2}

if \ \ \ \omega =\omega_p,\varepsilon(\omega)=0,k=0,\lambda =\frac{2 \pi}{k}=\infty

the propagation mode with \omega_p对应于均匀震荡电子气在金属中，这个模式称为等离子震荡模式

 给出了电磁波的金属中的传播条件

 

相关文章：

德鲁特金属导电理论（Drude）

德鲁特模型的重要等式 首先我们建立德鲁特模型的重要等式 我们把原子对于电子的阻碍作用，用一个冲量近似表示出来 在式子 首先定义一个等效加速度 由于 我们可以得到电导率的微观表达式 在交流电环境中 电场的表达式 借鉴上一问的公式 我们可以列出这样的表达式…...

编程日记 2023/5/12 11:45:44

（十一）python网络爬虫（理论+实战）——html解析库：BeautfulSoup详解

系列文章： python网络爬虫专栏 目录 序言 本节学习目标 特别申明...

编程日记 2023/5/12 11:45:36

四轮两驱小车（五）：蓝牙HC-08通信

前言： 在我没接触蓝牙之前，我觉得蓝牙模块应用起来应该挺麻烦，后来发觉这个蓝牙模块的应用本质无非就是一个串口 蓝牙模块： 这是我从某宝上买到的蓝牙模块HC-08，价格还算可以，而且可以适用于大多数蓝牙调试…...

编程日记 2023/5/12 11:45:30

华为OD机试题 - 对称美学（JavaScript）| 机考必刷

华为OD机试题 最近更新的博客使用说明本篇题解：对称美学题目输入输出示例一输入输出说明示例二输入输出备注Code解题思路华为OD其它语言版本最近更新的博客 华为od 2023 | 什么是华为od，od 薪资待遇，od机试题清单华为OD机试真题大全，用 Python 解华为机试题 | 机试宝典...

编程日记 2023/5/12 11:45:24

Web Spider案例 网洛克 第四题 JSFuck加密 练习(八)

声明 此次案例只为学习交流使用，抓包内容、敏感网址、数据接口均已做脱敏处理，切勿用于其他非法用途； 文章目录声明一、资源推荐二、逆向目标三、抓包分析 & 下断分析逆向3.1 抓包分析3.2 下断分析逆向拿到混淆JS代码3.3 JSFuck解决方式…...

编程日记 2023/5/12 11:45:19

【JavaScript速成之路】JavaScript数组

📃个人主页：「小杨」的csdn博客 🔥系列专栏：【JavaScript速成之路】 🐳希望大家多多支持🥰一起进步呀！ 文章目录前言1，初识数组1.1，数组1.2，创建数组1.3&…...

编程日记 2023/5/12 11:45:10

路由传参含对象数据刷新页面数据丢失

目录 一、问题描述 二、 解决办法 一、问题描述 【1】众所周知，在veu项目开发过程中，我们常常会用到通过路由的方式在页面中传递数据。但是用到this.$route.query.ObjectData的页面，刷新后会导致this.$route.query.ObjectData数据丢失。 …...

编程日记 2023/5/12 11:44:59

大数据flink框架入门分享(起源与发展、实时与离线计算、场景、处理流程、相关概念、特性普及、入门Demo)

文章目录起源与发展flink在github上的现状实时计算VS离线计算实时计算离线计算实时计算常用的场景框架流处理流程flink电商场景下的业务图示例flink中一些重要特性有界数据和无界数据时间语义、水位线事件时间处理时间水位线flink窗口概念理想中的数据处理含有延迟数据的数据处…...

编程日记 2023/5/12 11:44:49

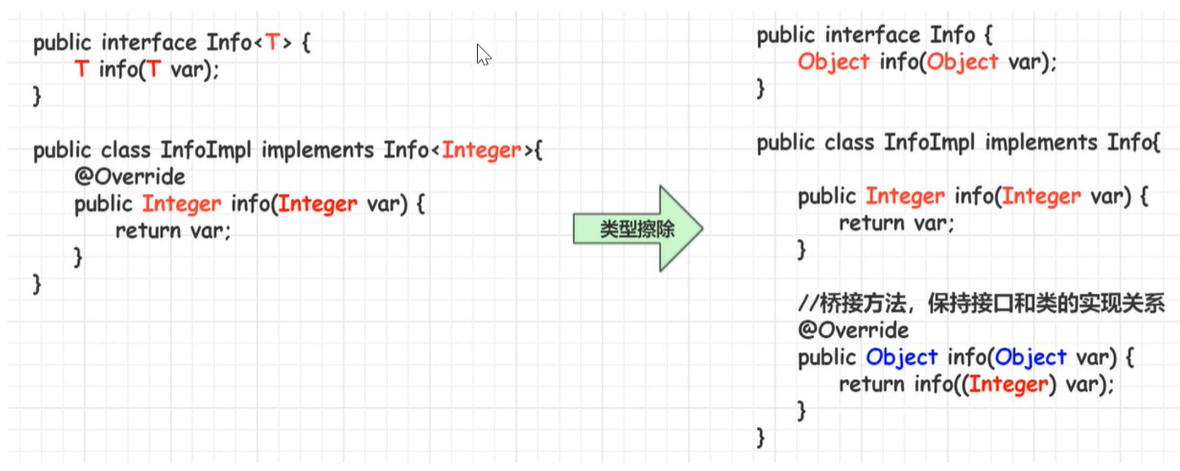
由点到面贯穿整个Java泛型理解

泛型概述 Java泛型(generics)是DK5中引入的一个新特性，泛型提供了编译时类型安全监测机制，该机制允许我们在编译时检测到非法的类型数据结构。 泛型的本质就是参数化类型，也就是所操作的数据类型被指定为一个参数。 如我们经常使用的Array…...

编程日记 2023/5/12 11:44:40

北斗RTK高精度定位在AI领域的应用

随着北斗高精度定位技术越来越成熟，通过GNSS高精度定位与机器人结合，越来越多的智能机器人走进我们生活中。像驾培机器人、智能除草机器人、智能巡检机器人、北斗划线机器人等智能机器人已经广泛的投入使用。驾培机器人驾培机器人：通考车安装…...

编程日记 2023/5/12 11:44:28

2023年再不会 IOC 源码，就要被淘汰了

👏作者简介：大家好，我是爱敲代码的小黄，独角兽企业的Java开发工程师，CSDN博客专家，阿里云专家博主📕系列专栏：Java设计模式、数据结构和算法、Kafka从入门到成神、Kafka从成神到升仙…...

编程日记 2023/5/12 11:44:23

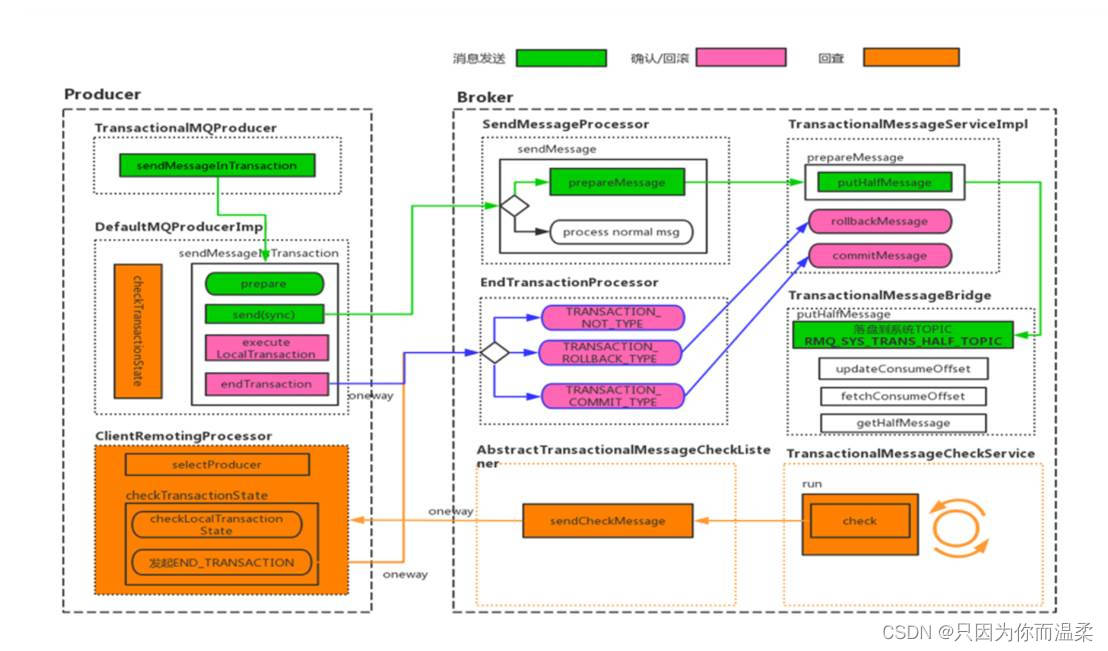
MQ面试题

1、为什么使用消息队列？ 其实就是问问你消息队列都有哪些使用场景，然后你项目里具体是什么场景，说说你在这个场景里用消息队列是什么？ 面试官问你这个问题，期望的一个回答是说，你们公司有个什么业务场景&…...

编程日记 2023/5/12 11:44:11

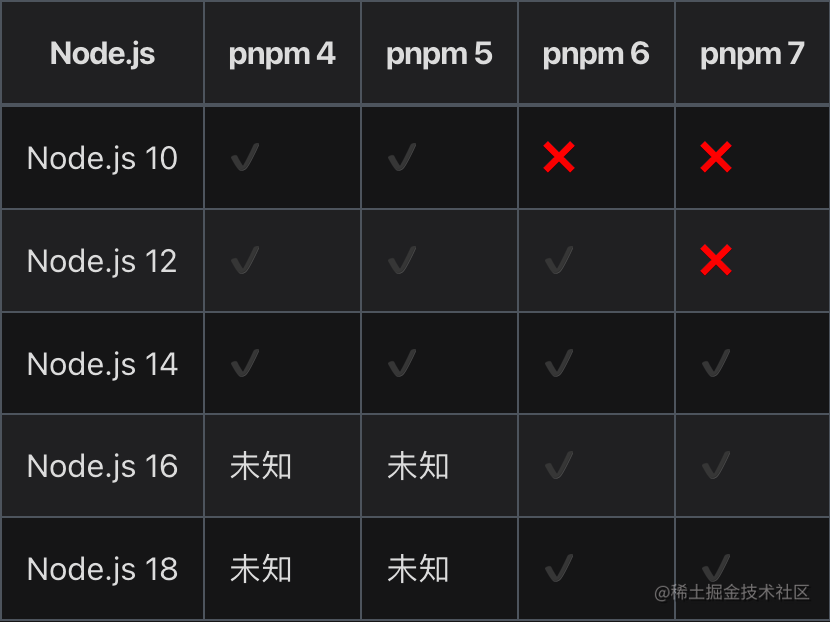
pnpm 基本详细使用（安装、卸载、使用）

一、简介 官网地址、GitHub地址、官方安装文档、官方卸载文档。 pnpm 全称 performant npm，意思为 高性能的 npm。pnpm 由 npm/yarn 衍生而来，解决了 npm/yarn 内部潜在的 bug，极大的优化了性能，扩展了使用场景。被誉为 最先进的…...

编程日记 2023/5/12 11:44:00

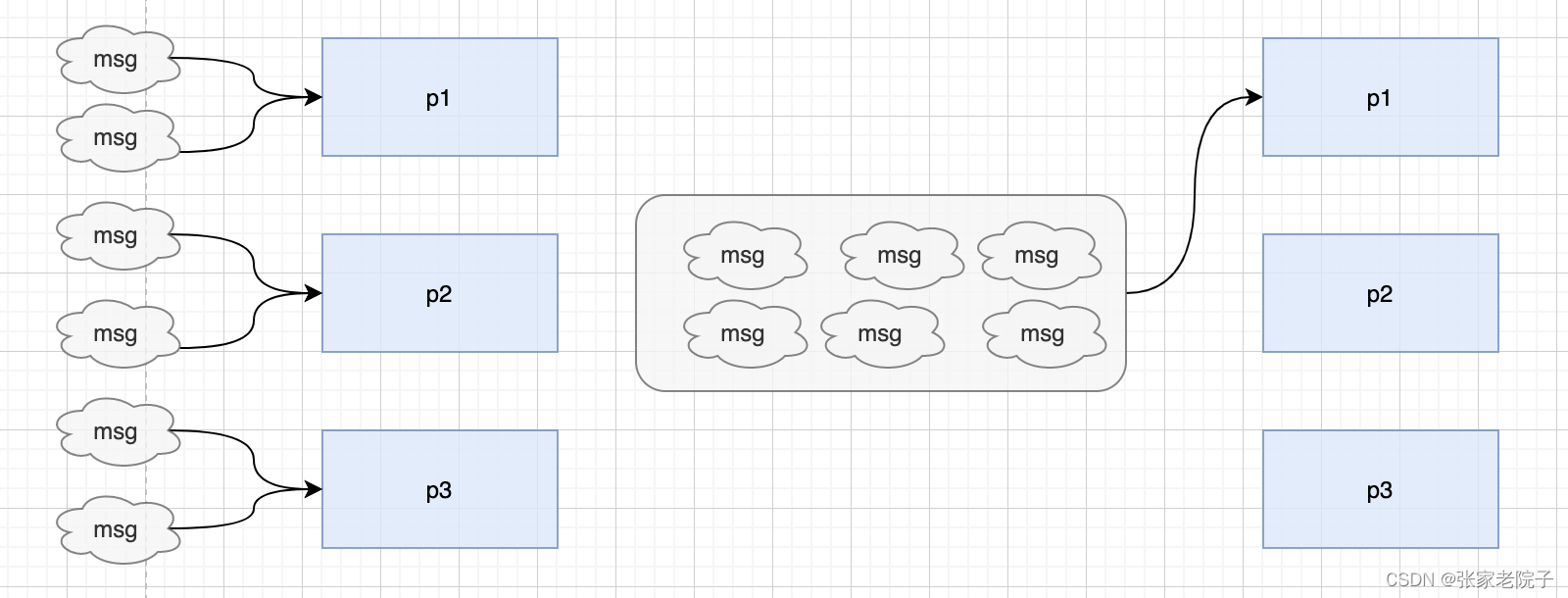
Kafka生产者的粘性分区算法

分区算法分类 kafka在生产者投递消息时，会根据是否有key采取不用策略来获取分区。 存在key时会根据key计算一个hash值，然后采用hash%分区数的方式获取对应的分区。 而不存在key时采用随机算法选取分区，然后将所有的消息封装到这个batch上直…...

编程日记 2023/5/12 11:43:52

java基础篇

1.基础篇注释注释是在程序指定位置添加的说明性信息注释不参与程序运行，仅起到说明作用单行注释 格式：// 注释信息多行注释 格式：/* 注释信息 */关键字关键字：就是被Java语言赋予了特定含义的单词java中共有53个关键字1.全部有小写…...

编程日记 2023/5/12 11:43:43

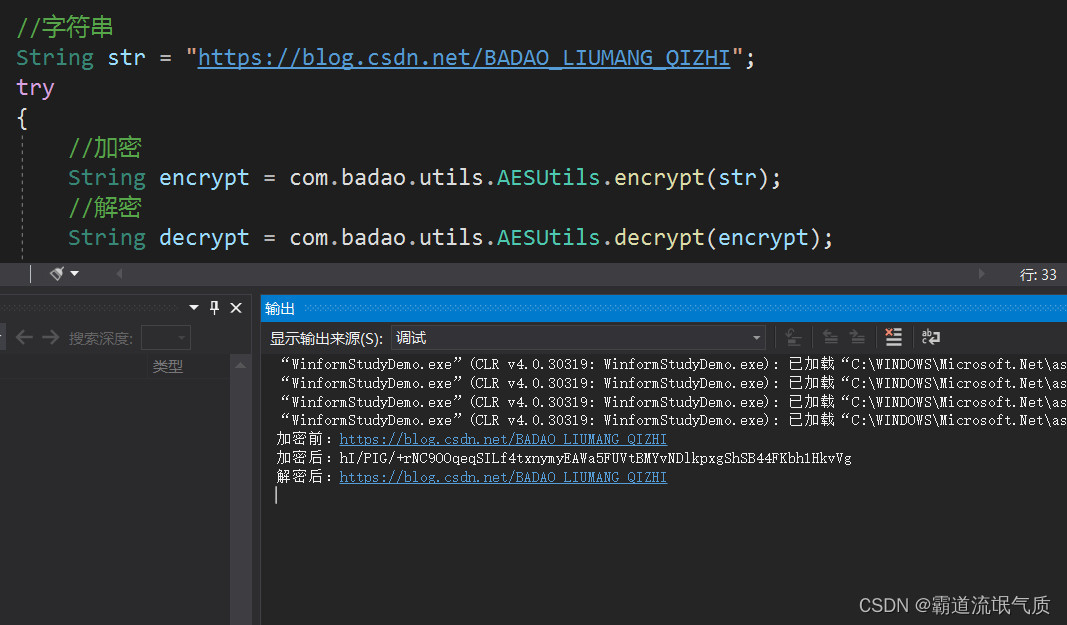
Java与Winform进行AES加解密数据传输的工具类与对应关系和示例

场景 AndroidJava中使用Aes对称加密的工具类与使用： AndroidJava中使用Aes对称加密的工具类与使用_霸道流氓气质的博客-CSDN博客 上面讲的Java与安卓进行数据传输时使用AES加解密的示例工具类。 如果Java需要与其他第三方平台比如Winform程序进行数据传递时也需…...

编程日记 2023/5/12 11:43:33

OpenAI模型的API调用与使用-测试（2）

OpenAI模型的API调用与使用-测试（2）1. 参考Quick start搭建一个demo1.1 安装openai包1.2 demo测试11.3 demo测试2参考资料1. 参考Quick start搭建一个demo 1.1 安装openai包 注意关掉科学上网工具，下载openai包 pip install openai安装好后…...

编程日记 2023/5/12 11:43:27

【LeetCode】剑指 Offer 22. 链表中倒数第k个节点 p136 -- Java Version

题目链接：https://leetcode.cn/problems/lian-biao-zhong-dao-shu-di-kge-jie-dian-lcof/ 1. 题目介绍（22. 链表中倒数第k个节点） 输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数&…...

编程日记 2023/5/12 11:43:06

经典卷积模型回顾7-轻量化模型MobileNet实现图像分类（matlab）

MobileNet是一种轻量级卷积神经网络，适用于较小的设备和低功耗环境。在MATLAB中，可以使用Deep Learning Toolbox进行MobileNet的图像分类训练。 使用预先训练好的MobileNet模型对自定义数据集进行微调训练： matlab % 导入数据集 imds im…...

编程日记 2023/5/12 11:42:59

程序员压力大？用 PyQt 做一个美*女GIF设置桌面，每天都有好心情

嗨害大家好鸭！我是小熊猫~ 要说程序员工作的最大压力不是来自于工作本身， 而是来自于需要不断学习才能更好地完成工作， 因为程序员工作中面对的编程语言是在不断更新的， 同时还要学习熟悉其他语言来提升竞争力… 好了&#xff0c…...

编程日记 2023/5/12 11:42:51

反向工程与模型迁移：打造未来商品详情API的可持续创新体系

在电商行业蓬勃发展的当下，商品详情API作为连接电商平台与开发者、商家及用户的关键纽带，其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息（如名称、价格、库存等）的获取与展示，已难以满足市场对个性化、智能…...

编程新知 2025/9/15 5:56:53

Nginx server_name 配置说明

Nginx 是一个高性能的反向代理和负载均衡服务器，其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机（Virtual Host）。 1. 简介 Nginx 使用 server_name 指令来确定…...

编程新知 2025/9/6 16:47:17

ETLCloud可能遇到的问题有哪些？常见坑位解析

数据集成平台ETLCloud，主要用于支持数据的抽取（Extract）、转换（Transform）和加载（Load）过程。提供了一个简洁直观的界面，以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

编程新知 2026/2/3 12:56:31

PL0语法，分析器实现！

简介 PL/0 是一种简单的编程语言，通常用于教学编译原理。它的语法结构清晰，功能包括常量定义、变量声明、过程（子程序）定义以及基本的控制结构（如条件语句和循环语句）。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言，由 Niklaus Wirth 设计，用于展示编译原理的核…...

编程新知 2026/1/29 17:06:33

学习STC51单片机32（芯片为STC89C52RCRC）OLED显示屏2

每日一言 今天的每一份坚持，都是在为未来积攒底气。 案例：OLED显示一个A 这边观察到一个点，怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 ： 如果代码里信号切换太快（比如 SDA 刚变，SCL 立刻变&#…...

编程新知 2026/2/6 0:50:24

Java线上CPU飙高问题排查全指南

一、引言 在Java应用的线上运行环境中，CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时，通常会导致应用响应缓慢，甚至服务不可用，严重影响用户体验和业务运行。因此，掌握一套科学有效的CPU飙高问题排查方法&…...

编程新知 2025/11/2 5:30:15

AI，如何重构理解、匹配与决策？

AI 时代，我们如何理解消费？ 作者｜王彬 封面｜Unplash 人们通过信息理解世界。 曾几何时，PC 与移动互联网重塑了人们的购物路径：信息变得唾手可得，商品决策变得高度依赖内容。 但 AI 时代的来…...

编程新知 2026/1/30 2:33:11

A2A JS SDK 完整教程：快速入门指南

目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库&#xff…...

编程新知 2025/12/12 8:42:24

CSS | transition 和 transform的用处和区别

省流总结： transform用于变换/变形，transition是动画控制器 transform 用来对元素进行变形，常见的操作如下，它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

编程新知 2025/10/17 20:59:57

iview框架主题色的应用

1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题，无需引入，直接可…...

编程新知 2026/1/31 9:29:45