【刷题笔记】笔记一
1.自守数
牛客链接
解析:
1.自守数的结尾肯定是 0,1,5,6
2.把数字转换为string类(方便比较)
3.直接find在s2 里面 使用find查找另一个即可。
#include <iostream>
#include<string>
using namespace std;int fun(int n)
{int ret =0;for(int i=0;i<=n;i++){if(i%10 == 0 || i%10 == 5 ||i%10 == 6 ||i%10 ==1){long j =i*i;string s1 = to_string(i);string s2 = to_string(j);int pos = s2.size() - s1.size();if(s2.find(s1,pos) != string::npos){ret++;}} }return ret;
}
int main() {int n;while (cin >> n) { cout<<fun(n)<<endl;}return 0;
}知识点:
1,to_string()函数。
2,find的返回值 string::npos
2.返回小于 N 的质数个数
题目链接
#include <iostream>
using namespace std;
bool fun(int n){for(int i = 2; i*i <= n; i++){if(n%i == 0){return false;}}return true;
}int main() {int n;int ret = 0; while(cin>>n){ret =0;for(int i = 3; i<n; i+=2){if(fun(i)){ret++;}}}cout<<ret+1;return 0;
}知识点:
1,除了2 质数只能是奇数。
1,验证N是否是质数的时候只需要从2验证到N开根号即可。
3.只出现一次的数字
oj链接
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for(auto n :nums){ret ^= n;}return ret;}
};4.杨辉三角(vector)
oj链接
class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> vv;vv.resize(numRows);//不给初始化值,就会调用vector<int> 的默认构造。for(size_t i =0; i<vv.size();i++){vv[i].resize(i+1, 0);vv[i][0] = vv[i][vv[i].size()-1] = 1;}for(int i =0; i< vv.size(); i++){for(int j=0; j< vv[i].size(); j++){if(vv[i][j] == 0){vv[i][j] = vv[i-1][j] +vv[i-1][j-1];}}}return vv;}
};这里使用c++ vector 很方便 比 C语言简单的多。
注意区分和c语言的区别。
5.电话号码的字母组合(递归)
oj题目
class Solution {string _numstr[10] = {"","","abc","def","ghi","jkl","mno", "pqrs", "tuv","wxyz"};
public:void combine(const string& digits,size_t i , vector<string>& ret, string tmp){if(i == digits.size()){ret.push_back(tmp);return;}size_t num = digits[i] - '0';for(auto ch :_numstr[num]){combine(digits, i+1, ret, tmp+ch);}}vector<string> letterCombinations(string digits) {//digits存放的是数字字符串vector<string> ret;//返回的值if(digits.empty()){return ret;}string tmp;//记录此深度的字符串组合size_t i =0;combine(digits,i,ret,tmp);return ret;}
};深度体会递归的思想
这个题主要是,那些不够直观。
本质是一个二叉树的深度遍历
6.删除有序数组中的重复项
题目链接
class Solution {
public:int removeDuplicates(vector<int>& nums) {int i =0;for(auto n : nums)if(n != nums[i]) nums[++i] = n;return i+1;}
};其实就是快慢指针(双指针)
7.只出现一次的数字 II
题目oj
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for(int i = 0 ;i< 32; i++){int val =0;for(auto j : nums){val += (j>>i)&1;}if(val % 3 ){ret += (1<<i);}}return ret;}
};//法二:
class Solution {
public:int singleNumber(vector<int>& nums) {sort(nums.begin(),nums.end());int i = 0;while(i < nums.size()-1){if(nums[i] == nums[i+1] && nums[i+1]== nums[i+2]){i += 3;}else{return nums[i];}}return nums[i];}
};
8.只出现一次的数字 III
题目oj
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {vector<int> ret;int val = 0;for(int i : nums){val ^= i;}int i=0;for( i = 0; i <32 ;i++){if((val >> i )& 1 == 1){break;}}vector<int> v1;vector<int> v2;for(int a : nums){if((a>>i)&1 == 1){v1.push_back(a);}else{v2.push_back(a);}}int b =0;for(int a: v1){b^=a;}ret.push_back(b);b=0;for(int a: v2){b^= a;}ret.push_back(b);return ret;}
};9.数组中出现次数超过一半的数字
题目链接
class Solution {
public:int MoreThanHalfNum_Solution(vector<int> numbers) {sort(numbers.begin(), numbers.end());return numbers[numbers.size()/2];}
};学完vector后这个题目就很简单了,直接排序,取中即可。
10.最小的K个数
题目oj
class Solution {
public:vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {vector<int> ret ;sort(input.begin(),input.end());for(int i =0;i<k;i++){ret.push_back(input[i]);}return ret;}
};知识点:
典型的topk问题,可以使用快排(sort的底层就是快排),堆排序(建立大小堆的问题)。
相关文章:

【刷题笔记】笔记一
1.自守数牛客链接解析:1.自守数的结尾肯定是 0,1,5,62.把数字转换为string类(方便比较)3.直接find在s2 里面 使用find查找另一个即可。#include <iostream> #include<string> using namespace …...

浏览器主页被hao123劫持的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理…...
| 含代码编写思路)
华为OD机试题 - 热点网络统计(JavaScript)| 含代码编写思路
华为OD机试题 最近更新的博客使用说明本篇题解:热点网络统计题目输入输出描述示例一输入输出示例二输入输出Code解题思路华为OD其它语言版本最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华…...

IT项目经理的自我修养手册
在不断进步的时代,任何岗位职责都是一个责任、权力与义务的综合体,有多大的权力就应该承担多大的责任,有多大的权力和责任应该尽多大的义务,任何割裂开来的做法都会发生问题。那么作为IT项目经理的岗位职责,我大概列举…...

2023年软考中级电子商务设计师考什么?
首先,电子商务设计师属于软考中级,因此难度也不是特别大。但并不是说就完全没有难度,难度还是有的,像上午题一般把基本知识点掌握了,是没什么问题的,重点就在于下午题会比较难。 接下来我们来剖析一下考试…...
现在的00后太强了,几个问题差点给我问懵了
前言 我们公司刚入职一个00后小伙,今天在办公室交流了一下,他问我会不会自动化测试,我说懂一点,然后直接问了我几个自动化测试问题,差点直接给我问懵了! 问题如下: 我们在制定自动化测试实施…...
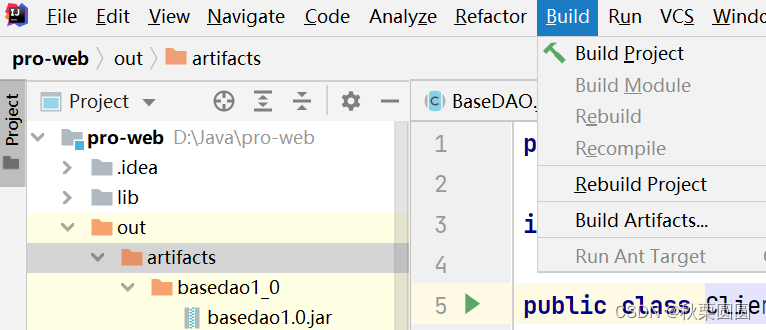
$3 : 水项目实战 - 水果库存系统
javase知识点复习: final关键字:http://t.csdn.cn/bvFgu 接口的定义,特性,实现,继承:http://t.csdn.cn/tbXl3 异常:http://t.csdn.cn/VlS0Z DAO的概念和角色(设计理念)&a…...

毕业设计 基于STM32单片机无线ZIGBEE智能大棚土壤湿度光照检测
基于STM32单片机无线ZIGBEE智能大棚土壤湿度光照检测1、项目简介1.1 系统构成1.2 系统功能2、部分电路设计2.1 STM32F103C8T6核心系统电路设计2.2 光敏采集电路设计2.3 温度采集电路设计3、部分代码展示3.1 读取DS18B20温度值3.2 定时器初始化1、项目简介 选题指导,…...
)
华为OD机试真题Java实现【相对开音节】真题+解题思路+代码(20222023)
相对开音节 题目 相对开音节构成的结构为辅音+元音(aeiou)+辅音(r除外)+e,常见的单词有bike、cake等。 给定一个字符串,以空格为分隔符,反转每个单词中的字母,若单词中包含如数字等其他非字母时不进行反转。 反转后计算其中含有相对开音节结构的子串个数(连续的子串…...
)
【C++】30h速成C++从入门到精通(STL容器listvector)
listlist的介绍list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中通过指针指向其前一个元素和后一个元素。list与…...

操作系统---存储管理
存储管理 操作系统将外存的文件调入到内存中,以便CPU调用,如果调用的内容不在内存中,则会产生缺页中断;产生缺页中断后,这事需要从外存调数据到内存中,然后CPU接着从断点继续调用内存中的数据;在…...
| 含思路)
华为OD机试题 - 好朋友(JavaScript)| 含思路
华为OD机试题 最近更新的博客使用说明本篇题解:好朋友题目输入输出示例一输入输出说明示例二输入输出说明Code解题思路华为OD其它语言版本最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典...
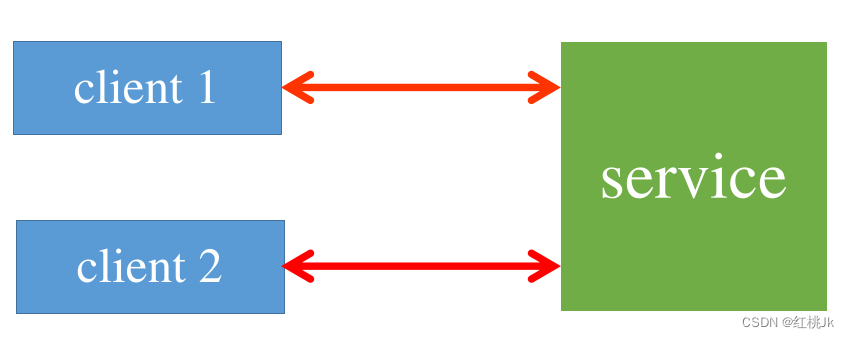
socket本地多进程通信基本使用方法和示例
目录 前言: socket是什么 socket基本原理框图 socket基本函数 1 socket() 函数 2 bind()函数 3 connect()函数 4 listen() 函数 5 accept() 函数 6 read() write() send() recv()函数 7 close()函数 8 字节序转换(hton) 示例代码 …...
Python 算法交易实验51 Step2 Signals 信号生成
说明 不可不读书 先从经典的一些超简单信号开始 使用移动平均指标SMA(算术) 给出了信号的产生方法,还有一些测算结果,反正看起来都是盈利的 首先使用离线方法实验一组结果,然后就使用ADBS来进行类似的处理。 内容 1 原理分析…...
app上架专用软著认证电子版权在主流应用商店的使用说明2023年最新版
软著认证电子版权在主流应用商店的使用说明 目录 一、 华为应用商店 二、 腾讯应用宝 三、 小米开放平台 小米应用提交: 小米游戏提交: 四、 OPPO开放平台 OPPO应用提交: OPPO游戏(App)提交: OPPO小游戏(快应…...

[Mybatis2]Mapper代理开发
文章目录 问题情境 代理开发 遵循的三条原则 1.定义与SQL映射文件同名的Mapper接口,并且将Mapper接口和SQL映射文件放置在同一目录下 2.设置SQL映射文件的namespace属性为Mapper接口的全限定名 3.在Mapper接口中定义方法,方法名就是SQL映射文件中sql…...

第十一届蓝桥杯大赛青少组国赛Python真题2
第十一届蓝桥杯大赛青少组Python 真题 第二题 提示信息: 杨辉三角形,是二项式系数在三角形中的一种几何排列。中国南宋数学家杨辉在 1261 年所著的《详 解九章算法》一书有明确记载。欧洲数学家帕斯卡在 1654 年发现这一规律,所以又叫做帕斯卡…...
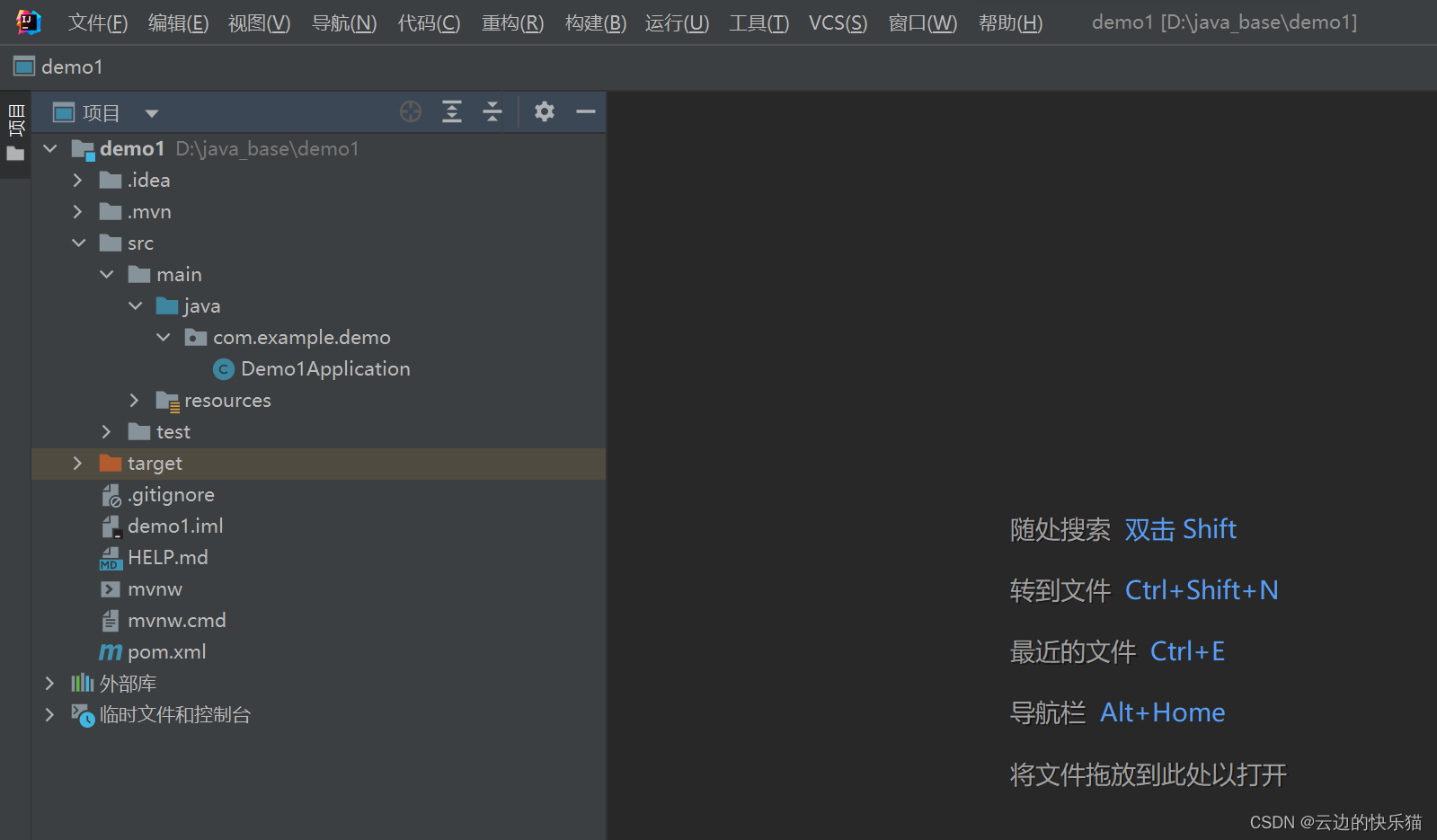
创建springboot项目文件报红
目录 一、遇到问题 二、出现这个问题的原因 三、解决办法 三种方法 四、操作步骤 一、遇到问题 创建springboot项目的时候,会发现一些重要文件都变成红色了,但是不影响程序的运行。只是看起来会有点不舒服。 二、出现这个问题的原因 因为这个spr…...
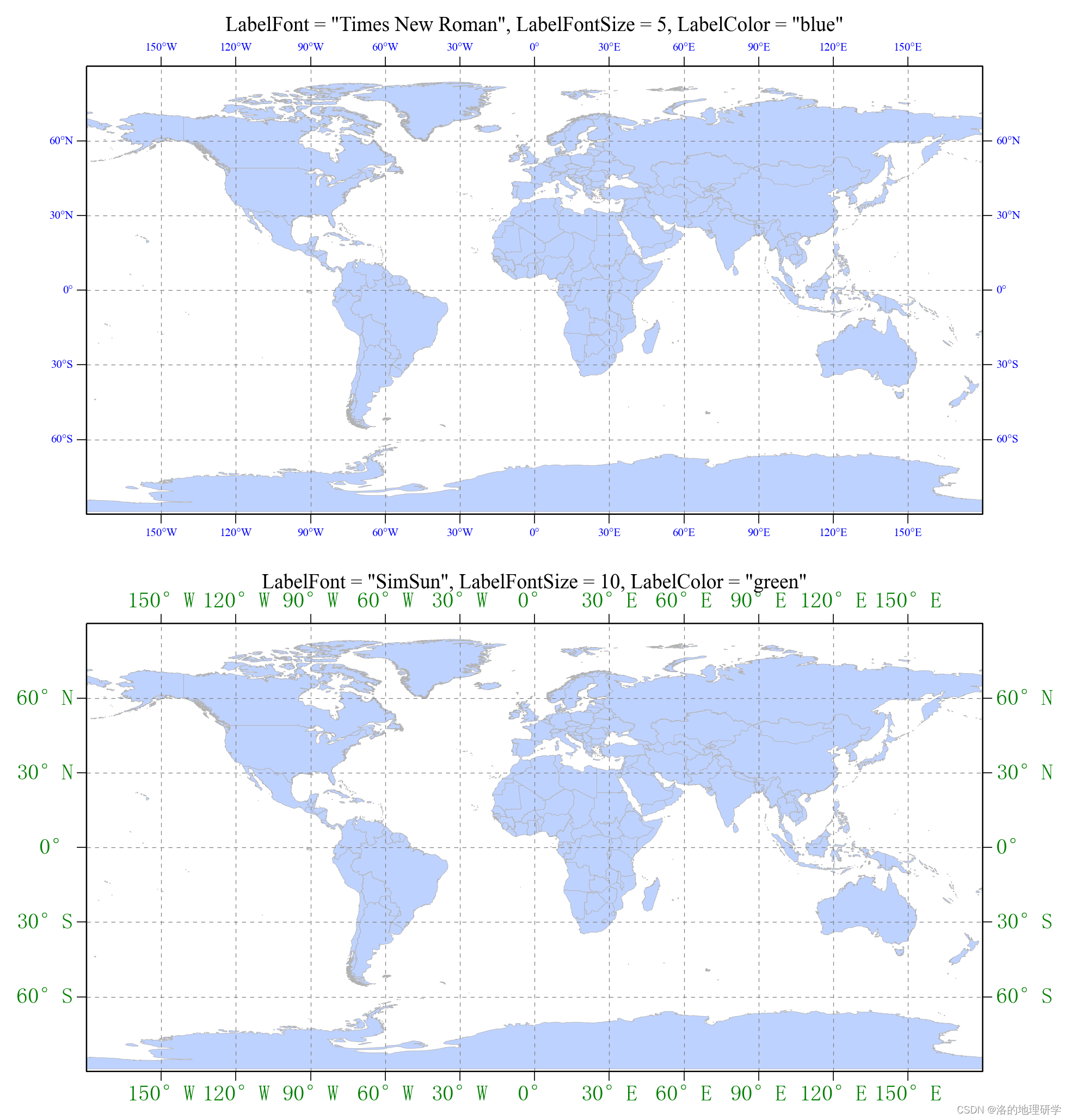
gma 地理空间绘图:(1) 绘制简单的世界地图-3.设置地图框
内容回顾 gma 地理空间绘图:(1) 绘制简单的世界地图-1.地图绘制与细节调整 gma 地理空间绘图:(1) 绘制简单的世界地图-2.设置经纬网 方法 SetFrame(FrameColor ‘black’, FrameWidth 0.6, ShowFrame True, ShowLeft True, ShowBottom True, Sho…...
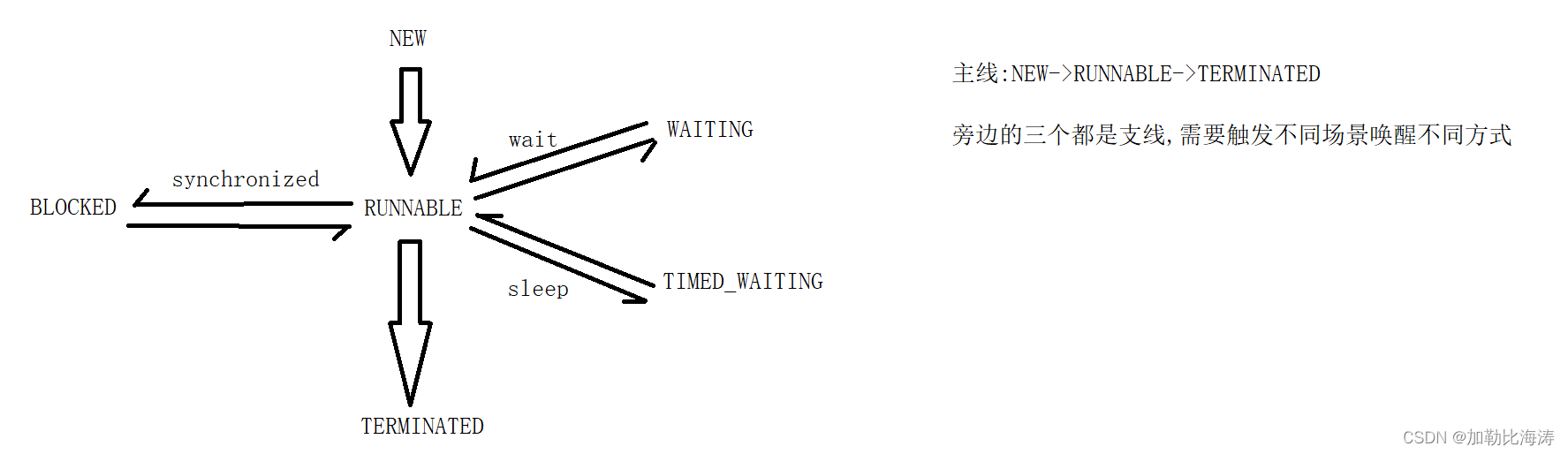
Java Web 实战 03 - 多线程基础(2)
Java Web 实战 03 - 多线程基础篇 2二 . Thread类常见方法2.1 Thread 的常见构造方法2.2 Thread 的几个常见属性getId()getName()getState()getPriority()isDaemon()案例 : 实现 getId()、getName()、 getState()、getPriority()、isDaemon()、isAlive()2.3 启动一个线程-start…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
