python 基础知识点(蓝桥杯python科目个人复习计划59)
今日复习内容:做题
例题1:建造房屋
问题描述:
小蓝和小桥是两位年轻的建筑师,他们正在设计一座新的城市。
在这个城市中,有N条街道,每条街道上有M个位置可以建造房屋(一个位置只能建造一个房屋),建造一个房屋的费用是1元,小蓝和小桥共有k元的建造预算。
现在,他们想知道,一共有多少种建造方案,满足以下要求:
在每条街道上,至少建造一座房屋;
建造的总成本不能超过k元。
由于方案数可能很大,他们只需要输出答案对10^9 + 7取模的结果。
输入格式:
一行3个整数N,M(1 = N,M <= 30)和K(1 <= K <= N * M),分别表示街道数,街道位置数和预算。
输出格式:
一个整数,表示满足条件的方案数对10^9 + 7取模的结果。
参考答案:
mod = int(1e9) + 7
n,m,k = map(int,input().split())
f = [[0] * (k + 1) for i in range(n + 1)]
for i in range(k + 1):f[0][i] = 1
for i in range(1,n + 1):for j in range(k + 1):for z in range(1,m + 1):if j >= z:f[i][j] = (f[i][j] + f[i - 1][j - z]) % mod
print(f[n][k])运行结果:

以下是我对此题的理解:
这道题涉及动态规划,目标的计算在给定预算下,满足建造要求的方案数。
1.定义了一个二维数组f,其中f[i][j]表示在前i条街道上,总成本为j的方案数。
2.初始化数组f[0][i],表示在0条街道上,总成本为i的方案数,初始化为1,因为无论预算多少,都有一种方案(不建造任何房屋)。
3.使用3层循环,其中第一层循环遍历街道,第二层循环遍历总成本,第3层循环遍历每个街道上可建造的位置。
4.在内层循环中,检查当前总成本j是否大于街道上可建造的位置数z。如果满足条件,则需要更新f[i][j],加上之前街道i - 1上总成本为j - z的方案数。
5.最终输出结果为f[n][k],表示在前n条街道上,总成本为k的方案数。
n,m,k = map(int,input().split()):从标准输入读取三个整数,分别表示街道数n,街道位置数m和预算k
f = [[0] * (k + 1) for i in range(n + 1):这一行代码创建了一个二维列表f,其中包含n + 1行,每行包含k + 1个元素,初始值都为0,这个列表用于存储动态规划过程中的中间结果。
for i in range(k + 1):这个循环遍历了k + 1个预算值,用于初始化第0条街道上的方案数。
f[0][i] = 1:这一行将第0条街道上总成本为i的方案数记为1,因为无论预算多少,都要一个方案,不建造任何房屋。
for i in range(1,n + 1):这个循环遍历了1到n条街道
for j in range(k + 1):这个循环遍历了k + 1个总成本值,,用于计算每条街道上的方案数
for z in range(1,m + 1):这个循环遍历了每个街道上可建造的位置数,从1到m
if j >= z:这个条件判断语句检查当前总成本j是否大于等于当前街道上可建造的位置数z
f[i][j] = (f[i][j] + f[i - 1][j - z]) % mod:这一行更新了当前街道上总成本为j的方案数。它将之前街道i - 1上总成本为j - z的方案数加到当前街道上,并对结果取模。
print(f[n][k]):最后输出结果,表示前n条街道上,总成本为k的方案数。
例题2:破损的楼梯
问题描述:
小蓝来到了一座高耸的楼梯前,楼梯共有N级台阶,从第0级台阶出发。小蓝可以迈上1或2级台阶。但是,楼梯上的第a1级,第a2级,第a3级,以此类推,共M级台阶的台阶面坏掉了,不能踩上去。
现在,小蓝想要到达楼梯的顶端,也就是第N级台阶,但他不能踩到坏了的台阶上,请问他有多少种不能踩到坏了的楼梯但是能到达第N级台阶的方案数?
由于方案数很大,请输出其对10^9 + 7的结果。
输入格式:
第一行包含两个正整数N(1 <= N <= 10^5)和M(0 <= M <= N),表示台阶总数和坏了的台阶级数。
接下来来N行,包含N个整数a1,a2,...,aM,(1 <= a1 < a2 <... < aM <= N),表示坏掉的台阶编号。
输出格式:
输出一个整数,表示小蓝到达楼梯顶层的方案数,对10^9 + 7取模。
参考答案:
mod = int(1e9) + 7
n,m = map(int,input().split())
mm = list(map(int,input().split()))
vis = [0] * (n + 1)
for i in mm:vis[i] = 1
f = [0] * (n + 1)
f[0] = 1
f[1] = 1 - vis[1]
for i in range(2,n + 1):if not vis[i]:f[i] = (f[i - 1] + f[i - 2]) % mod
print(f[n])运行结果:
以下是我对此题的理解:
这个题是一个很经典的冬天规划问题,以下是我的思路:
n,m = map(int,input().split()):从标准输入中读取两个整数,分别表示台阶总数和坏了的台阶数。
mm = list(map(int,input().split())):从输入中读取坏了的台阶的编号,并将它们储存在列表mm中
vis = [0] * (n + 1):创建了一个长度为n + 1的列表,用于标记每个台阶是否坏掉。如果台阶i坏了,则vis[i]的值为1,否则为0.
for i in mm:vis[i] = 1:这个循环将坏掉的台阶编号所对应的vis列表中的值记为1,表示这些台阶坏了。
f = [0] * (n + 1):用于存储动态规划过程中的中间结果,f[i]表示到达第i级台阶的方案数
f[0] = 1:初始第0级 台阶的方案数为0,因为小蓝从第0级台阶出发。
f[1] = 1 - vis[1]:初始化第一级台阶的方案数,如果第一级台阶坏了,则方案数为0,否则为1.
for i in range(2,n + 1):遍历剩下的台阶
if not vis[i]:用于判断此台阶是否坏了,如果没有,就继续执行下面的代码
f[i] = (f[i - 1] + f[i - 2]) % mod:这一行更新了到达第i级台阶的方案数,如果第i - 1级台阶坏了,只能通过第i - 2级台阶才能到达第i级台阶,这里需要考虑台阶的可行性。
print(f[n]):最终输出结果
例题3:拍照
问题描述:
小椒是个摄影爱好者。恰逢班级合照,他受邀帮忙拍照(站成一排)。这本是一件简单的事,但由于啾啾是个完美主义者,他希望拍的照片必须符合美学,即存在一个身高较大值,使得较大值无论往左还是往右身高都是递减的,数学上可以表示为:a[1] <= ... <= a[i] >= a[i + 1] >= ...>= a[n]。同学们已经站好了,但是不符合美学,你需要找出尽可能少的同学出列重新进行排列。请问最少需要出列几个同学?
输入格式:
第一行输入n,表示有n个同学,接下来的n行,输入校友身高,其中第i行输入a[i]( 1 <= i <= n),输入编号为i的校友的身高(单位是毫米)。
(1 <= n <= 100,1500 <= a[i] <= 1900)
输出格式:
输出一个整数,表示最少需要出队多少个同学。
参考答案:
n = int(input())
a = list(map(int, input().split()))
dp1 = [0] * (n + 1)
dp2 = [0] * (n + 1)for i in range(1, n + 1):dp1[i] = 1for j in range(1, i):if a[i - 1] >= a[j - 1]:dp1[i] = max(dp1[i], dp1[j] + 1)for i in range(n, 0, -1):dp2[i] = 1for j in range(n, i, -1):if a[i - 1] >= a[j - 1]:dp2[i] = max(dp2[i], dp2[j] + 1)ans = 0
for i in range(1, n + 1):ans = max(ans, dp1[i] + dp2[i] - 1)print(n - ans)运行结果:
以下是我对此题的理解:
n = int(input()):从标准输入读取同学的数量n
a = list(map(int,input().split())):从标准输入读取每个同学的身高,并将它们存储在列表a中
dp1和dp2分别代表从左到右和从右到左的动态规划数组。它们的长度都是n + 1,用于存储每个位置的最长符合美学要求的子序列长度。
对于dp1数组,dp1[i]表示以同学i为结束的最长符合美学要求的子序列长度,初始化所有值为1,因为每个同学本身就是一个符合美学要求的子序列
对于dp2数组,dp2[i]表示以同学i为开始的最长符合美学要求的子序列长度,初始化所有值为1,因为每个同学本身就是一个符合美学要求的子序列。
对于每个同学i,在dp1中遍历所有在i之前的同学j,之后就是比较,再输出答案就可以了。
OK,前几天写比赛论文去了,没时间复习,从今天开始,必须挤时间了。
那这篇就这样了,下一篇继续!
相关文章:

python 基础知识点(蓝桥杯python科目个人复习计划59)
今日复习内容:做题 例题1:建造房屋 问题描述: 小蓝和小桥是两位年轻的建筑师,他们正在设计一座新的城市。 在这个城市中,有N条街道,每条街道上有M个位置可以建造房屋(一个位置只能建造一个房…...
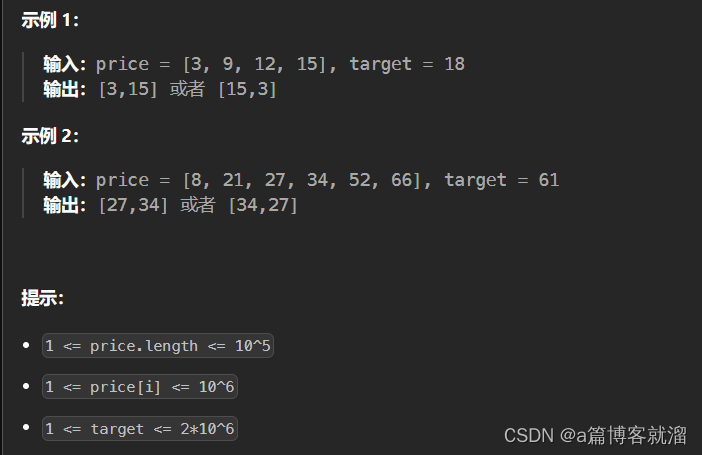
LCR 179. 查找总价格为目标值的两个商品 - 力扣
1. 题目 购物车内的商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况,返回任一结果即可。 2. 示例 3. 分析 题目有说明为递增数组,所以可以利用单调性双指针解决。跟611. 有效的三角形个数为一类题…...
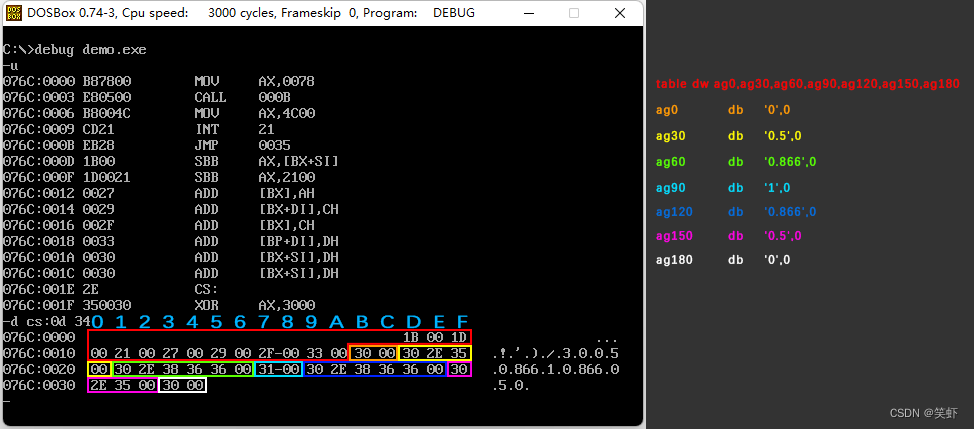
《汇编语言》- 读书笔记 - 第16章-直接定址表
《汇编语言》- 读书笔记 - 第16章-直接定址表 16.1 描述了单元长度的标号(数据标号)检测点 16.1 16.2 在其他段中使用数据标号assume通过标号取地址检测点 16.2 16.3 直接定址表(Direct Addressing Table)例1分析代码效果 例2分析…...

ChatGPT 新增朗读功能,支持 37 种语言
3 月 5 日消息,OpenAI 为其广受欢迎的聊天机器人 ChatGPT 推出了名为「朗读」(Read Aloud) 的新功能。该功能可以让 ChatGPT 用五种不同的声音朗读其回复,旨在为用户提供更加便捷的交互体验。目前,「朗读」功能已上线 ChatGPT 的网页端、iOS …...
洛谷 P8816 [CSP-J 2022] 上升点列(T4)
目录 题目传送门 算法解析 最终代码 提交结果 尾声 题目传送门 [CSP-J 2022] 上升点列 - 洛谷https://www.luogu.com.cn/problem/P8816 算法解析 k 0 且 xi, yi 值域不大时,这题是非常简单的 DP,类似「数字三角形」。 记 dp(x,y) 为「以 (x,y) …...
python爬虫(2)
继上节 查看数组维数 可以使用数组的ndim属性 代码示例如下: import numpy as np c np.random.randint(1,9,5) print(c.ndim) 结果如下: 当然这些也可以结合前面的各种用法来使用 1、选取数组元素 (1)一维数组的元素…...
外包干了8天,技术退步明显。。。。。
先说一下自己的情况,本科生,19年通过校招进入杭州某软件公司,干了接近3年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
浅谈去耦电容的作用、选择、布局及其它电容的区别!
在一些文章资料中,去耦电容器被认为是旁路电容器。在其他资料中,去耦电容和旁路电容的区别在于:“旁路电容以输入信号中的干扰为滤波对象,而去耦电容以输出信号的干扰为滤波对象,防止干扰信号返回到输出端。”力量。”…...
抖音视频评论批量采集软件|视频下载工具
《轻松搞定!视频评论批量采集软件,助您高效工作》 在短视频这个充满活力和创意的平台上,了解用户评论是了解市场和观众心声的重要途径之一。为了帮助您快速获取大量视频评论数据,我们推出了一款操作便捷、功能强大的软件ÿ…...

javaSE-----继承和多态
目录 一.初识继承: 1.1什么是继承,为什么需要继承: 1.2继承的概念与语法: 二.成员的访问: 2.1super关键字 2.2this和super的区别: 三.再谈初始化: 小结: 四.初识多态: 4.1多…...

数据库之Oracle数据导入导出
目录 一、单表导出和导入1、单表导出数据2、单表导入数据二、全表导出和导入1、远程导出全表数据2、导入本地数据三、密码带特殊字符的写法1、Windows OS写法2、Linux/Unix OS写法 四、总结 一、单表导出和导入 1、单表导出数据 --导出远程服务上的表数据 exp 用户名/密码IP…...

nRF52832——GPIOTE与外部中断
这里写目录标题 GPIOTE 原理分析GPIOTE 输入事件应用GPIOTE 事件寄存器应用GPIOTE 事件组件的应用(库函数)GPIOTE PORT 事件应用 GPIOTE 任务应用GPIOTE 任务触发 LED 寄存器操作组件方式进行任务配置 GPIOTE 原理分析 GPIO 任务和时间(GPIO…...
根据用户名称实现单点登录
一、参数格式 二、后端实现 Controller层 public class IAccessTokenLoginController extends BaseController {Autowiredprivate ISysUserService sysUserService;Autowiredprivate ISingleTokenServiceImpl tokenService;/*** 登录方法** return 结果*/PostMapping("/l…...

【设计】855. 考场就座
855. 考场就座 这段代码实现了一个考场安排座位的算法。在这个算法中,考场被模拟成一个从0到n-1的数轴,其中每个位置代表一个座位。目的是在每次学生入座时,找到一个使得所有学生之间距离最大化的座位,并在学生离开时更新座位信息…...
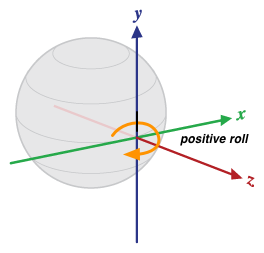
Android中的传感器类型和接口名称
本文将介绍传感器坐标轴、基础传感器和复合传感器(动作传感器、姿势传感器、未校准传感器和互动传感器)。 1. 传感器坐标轴 许多传感器的传感器事件值在相对于设备静止的特定坐标系中表示。 1.1 移动设备坐标轴 Sensor API 仅与屏幕的自然方向相关&a…...

解析进程 /proc/pid/maps 和 /proc/pid/smaps
目录 /proc//maps 背景 具体描述 代码实现 实践 /proc/pid/smaps smaps各子项详解 代码实现 代码调用的路径如下: 小结 /proc/<pid>/maps 背景 相对于/proc/meminfo和dumpsys meminfo可以看到系统整体的内存信息,我们还需要能够具体到…...
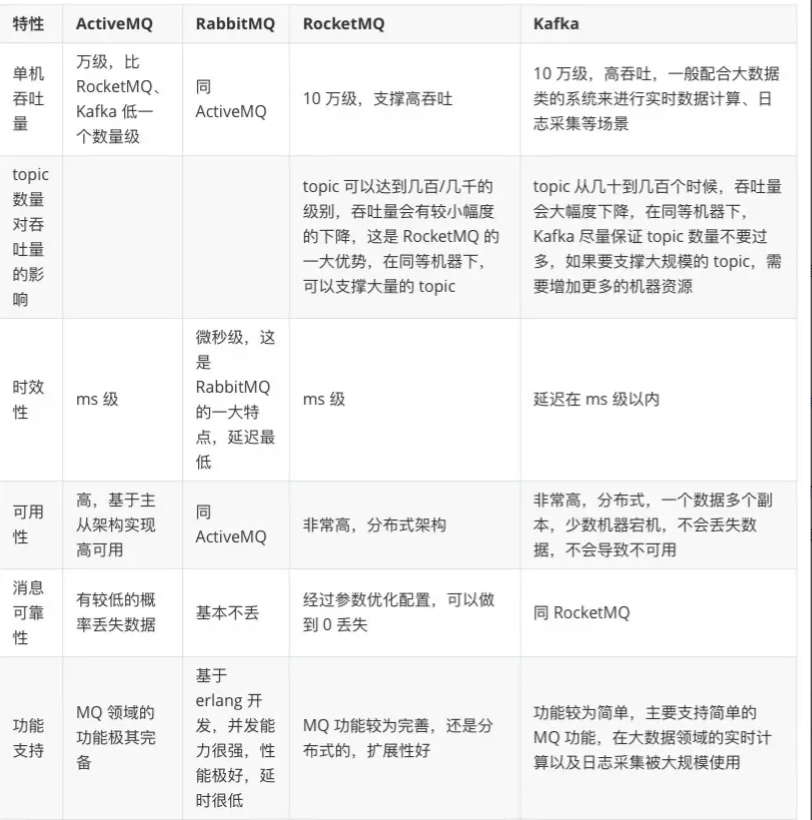
【MQ】消息队列概述
📝个人主页:五敷有你 🔥系列专栏:MQ ⛺️稳中求进,晒太阳 定义 消息队列:一般我们简称为MQ(Message Queue) Message Queue :消息队列中间件,很多初学者认为,MQ通过消息的发送…...
交友盲盒系统PHP开源的盲盒源码
源码介绍: 交友盲盒系统是一款基于PHP开发的开源免费盲盒系统,旨在为用户提供一个充满乐趣和惊喜的社交体验。该系统具有丰富的功能和灵活的扩展性,可以轻松地满足各种线上交友、抽奖活动等场景的需求。 安装说明: PHP版本&…...

【Flutter 面试题】什么是异步编程 Flutter中如何处理异步操作?
【Flutter 面试题】什么是异步编程 Flutter中如何处理异步操作? 文章目录 写在前面解答补充说明从网络API异步获取数据并解析 写在前面 关于我 ,小雨青年 👉 CSDN博客专家,GitChat专栏作者,阿里云社区专家博主&#x…...

处理error: remote origin already exists.及其Gitee文件上传保姆级教程
解决error: remote origin already exists.: 删除远程 Git 仓库 git remote rm origin 再添加远程 Git 仓库 git remote add origin (HTTPS) 比如这样: 然后再push过去就ok了 好多人可能还是不熟悉怎么将文件上传 Gitee:我…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
