[递归、搜索、回溯]----递归
前言
作者:小蜗牛向前冲
专栏:小蜗牛算法之路
专栏介绍:"蜗牛之道,攀登大厂高峰,让我们携手学习算法。在这个专栏中,将涵盖动态规划、贪心算法、回溯等高阶技巧,不定期为你奉上基础数据结构的精彩算法之旅。一同努力,追逐技术的星辰大海。"
目录
一、递归
1、什么是递归
2、为什么会用到递归
3、如何去理解递归
4、如何求写递归
二、搜索
1、深度和宽度
2、搜索
3、拓展搜索
三、回溯和剪枝
四、刷题时刻
1、汉诺塔问题
a、算法原理
b、代码实现
2、合并两个有序链表(easy)
a、算法原理
b、代码实现
3、反转链表(easy)
a、算法原理
b、代码实现
四、 两两交换链表中的节点(medium)
a、算法原理
b、代码实现
五、Pow(x, n)- 快速幂(medium)
a、算法原理
b、代码实现
这里是主讲算法刷题,一些概念可以看博主以前写的博客,下面会带链接。后面就不会在提醒了,大家开心刷题吧!
一、递归
1、什么是递归
简单的来说就是函数自调用自己。
在C语言的学习我们就接触了,然后在数据结构中的二叉数,快排,归并都有其身影。
不清楚看这里:
详解函数递归
[数据结构]~二叉树
[数据结构]-玩转八大排序(二)&&冒泡排序&&快速排序
[数据结构]-玩转八大排序(三)&&归并排序&&非比较排序
2、为什么会用到递归
本质是为由主问题拆分到子问题,再由相似的子问题拆分到相同的子问题。
如二叉树的遍历

快排
归并排序

3、如何去理解递归
初学可以画递归展开图
在求做二叉树的简单题目
最后宏观的看到递归过程:
- 不在拘泥于递归展开图
- 把递归想象为一个黑盒
- 让黑盒求完成任务
4、如何求写递归
- 先找到相同的子问题---->想函数的头。
- 只关心子问题是如何解决的---->写出函数主体
- 注意递归函数的出口
二、搜索
1、深度和宽度
深度优先遍历vs 深度优先搜索(dfs)
深度优先遍历
其中深度优先表示从根节点开始,沿着每个分支尽可能深入,直到达到树或图的最底部,然后回溯到上一层,继续遍历其他分支。在这个过程中,我们尽可能深入地探索一个分支,直到无法继续为止,然后回溯。
深度优先搜索(Depth-First Search,DFS):
用于描述在图或树等数据结构上进行搜索的算法。DFS 是一种算法,通过深度优先的方式遍历或搜索图或树。它通常与递归或使用栈的迭代方法结合使用。DFS 通常用于解决图的连通性问题、拓扑排序、路径查找等问题。
这二个概念其实在某种程度是是一样的:我们只要记住他就是一条路走到黑。
宽度优先遍历vs 宽度优先搜索(bfs)
宽度优先遍历(Breadth-First Traversal):
宽度优先遍历从根节点开始,逐层地访问节点,先访问距离根节点最近的节点,然后是相邻的、同一层级的节点,依此类推,直到遍历完整个数据结构。
宽度优先搜索(Breadth-First Search,BFS):
它从根节点开始,逐层地探索图中的节点,先探索距离起始节点最近的节点,然后是相邻的、同一层级的节点,依此类推,直到找到目标节点或者遍历完整个数据结构。
这二个概念其实在某种程度是是一样的:我们只要记住他就一层层走的。
2、搜索
简单的来说就是暴力枚举一遍所以数据。
通过dfs或者bfs .
3、拓展搜索
其实搜索不仅仅局限鱼树或图等数据结构问题求解,只要一个问题的子问题可以全排列为,一课树状图的问题都可以用搜索解决。
比如对于1,2,3进行全排列
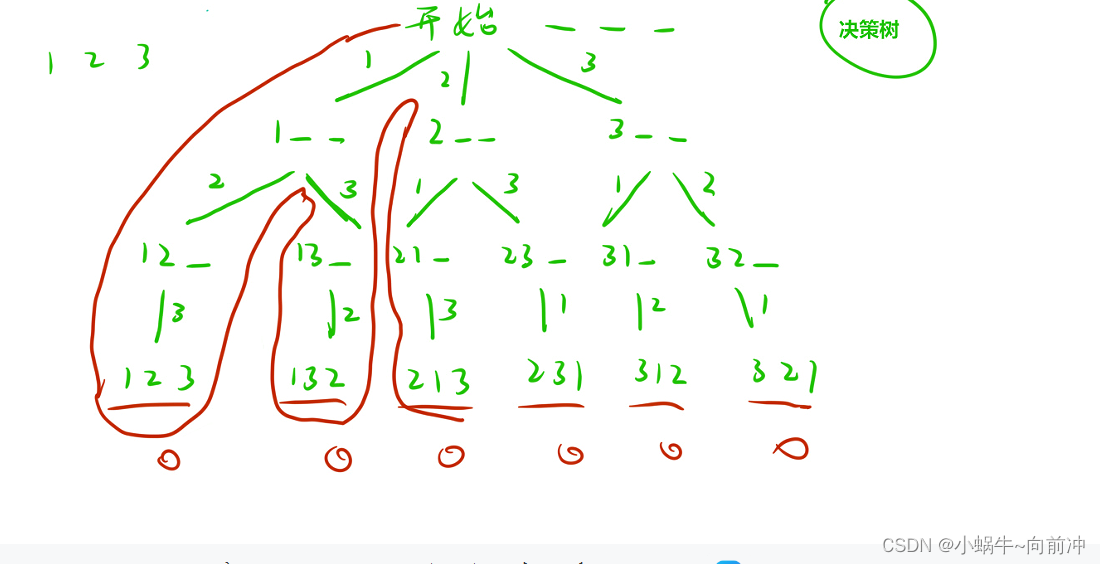
三、回溯和剪枝
回溯本质就是深搜,剪枝的本质就是将回溯过后发现不对的部分去掉。
拿下面的走迷宫举例:
=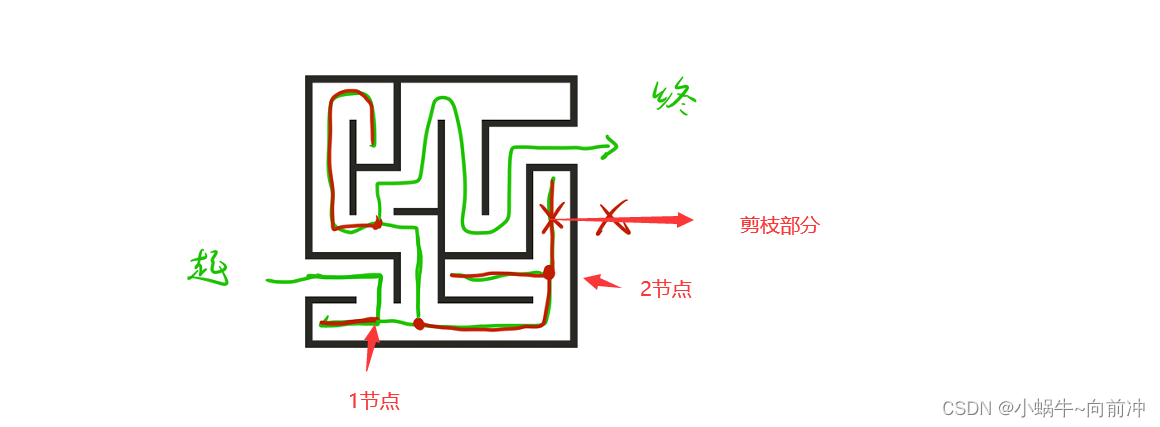
首先我们从起点出发通过深度搜索来都到1节点,有二条路,走向红色那一条,碰壁后返回的1节点的过程就是回溯。在来看2节点, 发现二路都不对,回溯后将那二条路去掉的过程就是剪枝。
四、刷题时刻
1、汉诺塔问题
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = [] 输出:C = [2, 1, 0]示例2:
输入:A = [1, 0], B = [], C = [] 输出:C = [1, 0]提示:
- A中盘子的数目不大于14个。
class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {}
};a、算法原理
拿到一个题目,我们完成对题意的理解后,首先会想:
怎么去解决这个问题?

一般情况:我们都是按照题意先试试着去模拟。
当N==1时:我们直接把一个盘子从A移动C
当N==2时:我们要想把大盘上面的小盘,放在B,在把大盘放在C后,将小盘移动过来C。
当N==3时:我们把大盘上面的部分想办法移动到B,然后在把大便移动到C,最后想办法将小盘部分移动到C就可以了、
当N==n,时候,重复上图序号的过程就可以了
这种情况不就,我们将一个大问题,转换为一个子问题,子问题在转换为,同类型的子问题。所以这就切合递归。
递归解题思路:
1、重复问题---函数头
重复问题:将x柱子上面的盘子,借助y柱子,移动到z柱子上
函数头: void dfs(x,y,z,n)
2、只关系子问题在做什么
这里以N==3来切入思考:
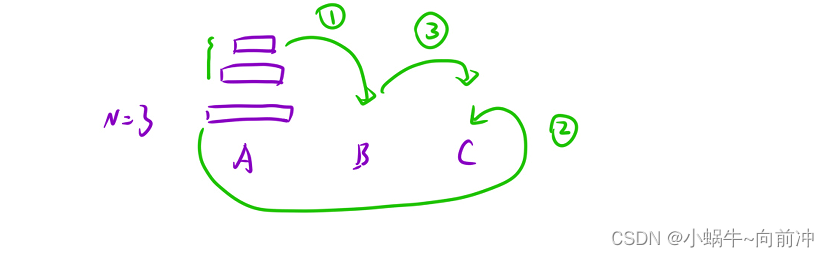
dfs(x,z,y,n-1) --- B 将大盘上面的盘子移走(1)
x.back() ---C 将大盘子移动到z柱子上(2)
dfs(y ,x,z)--->C 将小盘部分移动到z柱子上(3)
这里自己可以简单画图理解!
3、递归的出口在哪里
N==1的时候,我们就不要在借助其他盘子了,直接移动到z柱子上就可以了。
x.back() ---z;
b、代码实现
class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C){int n = A.size();dfs(A, B, C, n);}void dfs(vector<int>& x, vector<int>& y, vector<int>& z, int n){//递归出口if (n == 1){z.push_back(x.back());x.pop_back();return;}//函数体dfs(x, z, y, n - 1);z.push_back(x.back());x.pop_back();dfs(y, x, z, n - 1);}
};LeetCode测试:

2、合并两个有序链表(easy)
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]示例 2:
输入:l1 = [], l2 = [] 输出:[]示例 3:
输入:l1 = [], l2 = [0] 输出:[0]提示:
- 两个链表的节点数目范围是
[0, 50]-100 <= Node.val <= 100l1和l2均按 非递减顺序 排列1
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {}
};a、算法原理
合并二个升序的链表,我们只要先从二个链表头结点选出,最小的那个结点拿出来,其余形成二个新的链表,我们让函数dfs帮我们合成一个链表,在链接最小的那个结点。这不就相同的子问题吗?

所以我们这里可以用递归解决:
函数头:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
函数体:相同的子问题:
从二个链表头结点选出最小的那个list1(假设为最小)
list1->next = mergeTwoLists(list1->next, list2) ;
return list1;
递归结束:
那个链表为空就返回另外一个链表。
b、代码实现
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2){if (list1 == nullptr)return list2;if (list2 == nullptr)return list1;if (list1->val < list2->val){list1->next = mergeTwoLists(list1->next, list2);return list1;}else{list2->next = mergeTwoLists(list1, list2->next);return list2;}}
};LeetCode测试:

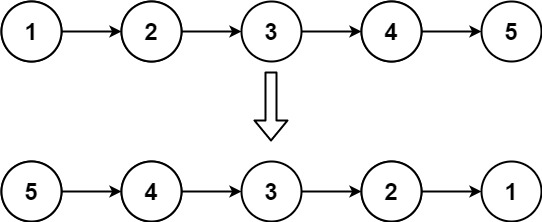
3、反转链表(easy)
给你单链表的头节点
head,请你反转链表,并返回反转后的链表。示例 1:
输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]示例 2:
输入:head = [1,2] 输出:[2,1]示例 3:
输入:head = [] 输出:[]提示:
- 链表中节点的数目范围是
[0, 5000]-5000 <= Node.val <= 5000进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {}
};a、算法原理
既然这道题目可以用递归解决问题,那么翻转整体链表,就可以分为一个子问题。
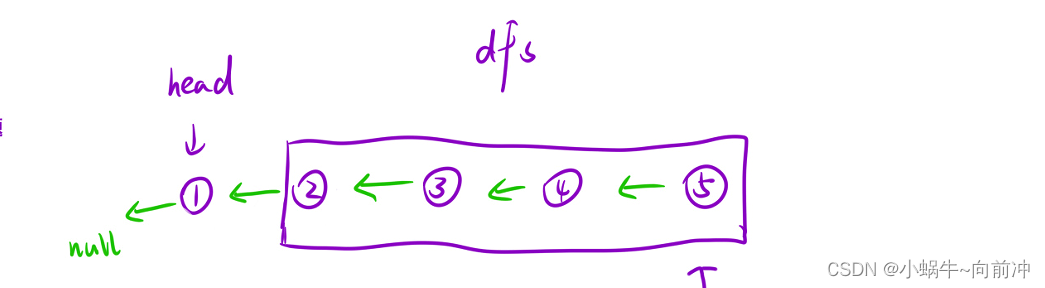
视角一:从宏观视角看
我们要翻转链表,可以分为:
- 让当前结点后面的结点链表进行逆置,返回头结点就好了
- 让当前结点添加到后面逆置链表即可
视角二:将链表看成一颗树
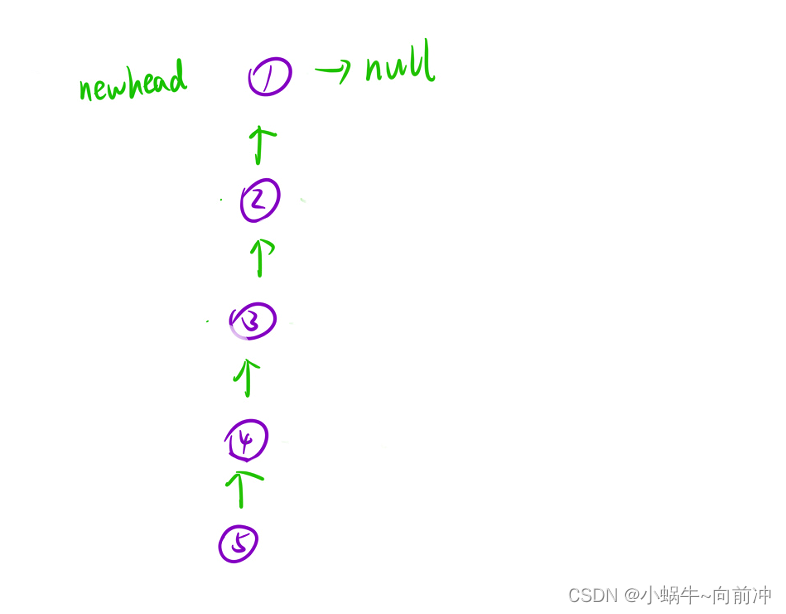
那不就只进行一次dfs遍历就好了(树的后序遍历)
递归实现:
函数头
ListNode* reverseList(ListNode* head)
子问题
ListNode* newhead = reverseList(head->next);
//将当前结点连接到逆置链表
head->next->next = head;
head->next = nullptr;
递归的出口在哪里
当head==nullptr 或者head->next==nullptr;
return head;
b、代码实现
class Solution {
public:ListNode* reverseList(ListNode* head){//一个结点或者没有结点就不需要逆置//细节不要这样会报错if(head->next==nullptr||head==nullptr)//表达式是有顺序的这样会先判断:head->next==nullptr//但是要是head为nullptr就是空指针的引用了if (head == nullptr || head->next == nullptr)return head;//子问题//返回逆置当前结点后面链表,返回新头结点ListNode* newhead = reverseList(head->next);//将当前结点连接到逆置链表head->next->next = head;head->next = nullptr;//返回新的头结点return newhead;}
};LeetCode测试:

四、 两两交换链表中的节点(medium)
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
输入:head = [1,2,3,4] 输出:[2,1,4,3]示例 2:
输入:head = [] 输出:[]示例 3:
输入:head = [1] 输出:[1]提示:
- 链表中节点的数目在范围
[0, 100]内0 <= Node.val <= 100
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {}
};a、算法原理
对于链表类问题,大家一定要画图前理解。

首先站宏观的视角看待,我们要将相邻二个结点交换,我们可以分为前二个结点,和后面一段,后面一段我们交给一个函数swapPairs我相信他一定能完成对里面结点进行交换,怎么完成的我们不关心。
然后在如图进行连接。
那递归结束的条件是什么:
当我们的结点为空或者只有一个节点就返回head.
b、代码实现
class Solution {
public:ListNode* swapPairs(ListNode* head){if (head == nullptr || head->next == nullptr)return head;ListNode* tmp = swapPairs(head->next->next);ListNode* newhead = head->next;newhead->next = head;head->next = tmp;return newhead;}
};LeetCode测试:

五、Pow(x, n)- 快速幂(medium)
实现 pow(x, n) ,即计算
x的整数n次幂函数(即,xn)。示例 1:
输入:x = 2.00000, n = 10 输出:1024.00000示例 2:
输入:x = 2.10000, n = 3 输出:9.26100示例 3:
输入:x = 2.00000, n = -2 输出:0.25000 解释:2-2 = 1/22 = 1/4 = 0.25
class Solution {
public:double myPow(double x, int n) {}
};a、算法原理
这道题目最容易想到是暴力,就是遍历相乘就好了,但是这样肯定是会超时的。
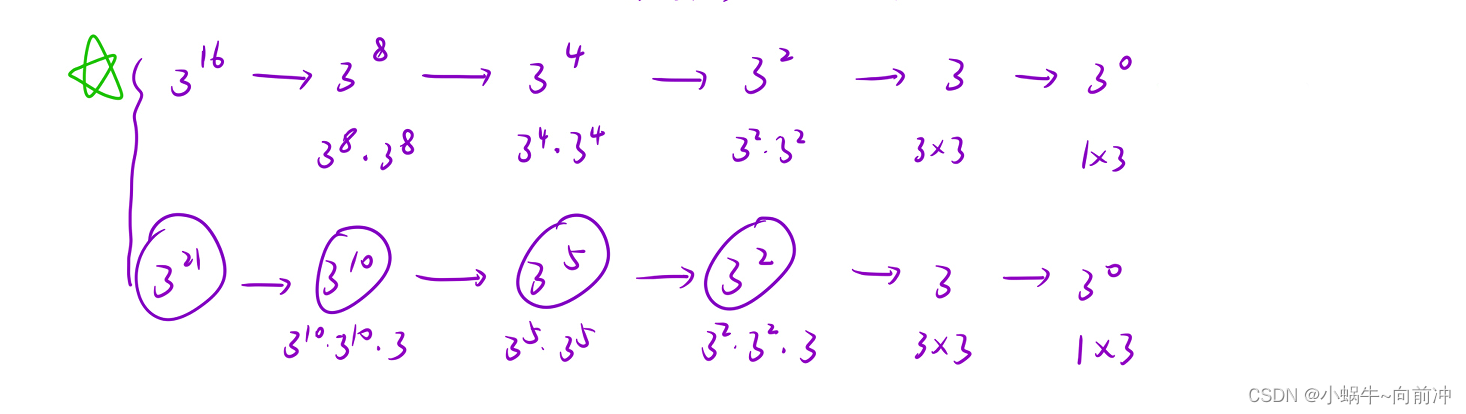
我们可以思考一下:当我们 x和n为上面二种情况的时候,我们通过不断划分子问题,从而求出结果,这不就是递归吗?
函数头:int pow(x,n)我们相信这函数可以帮助我们进行幂计算
函数体:只关系子问题做了什么
tmp = pow(x,n/2);
return n%2==0? tmp*tmp:tmp*tmp*x
递归出口:n==0时return 1;
细节问题:
n可能出现负数:
也就是说可能出现3^(-2) 那我们的计算结果应该是1/(3^(2))
n可能为
:
如果我们把他转换为正数处理,int是存放不下的,所以我们要用long long去存(进行强转)
b、代码实现
class Solution {
public:double myPow(double x, int n){return n > 0 ? Pow(x, n) : 1.0 / Pow(x, -(long long)n);}double Pow(double x, long long n){if (n == 0)return 1.0;double tmp = Pow(x, n / 2);return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;}
};
相关文章:

[递归、搜索、回溯]----递归
前言 作者:小蜗牛向前冲 专栏:小蜗牛算法之路 专栏介绍:"蜗牛之道,攀登大厂高峰,让我们携手学习算法。在这个专栏中,将涵盖动态规划、贪心算法、回溯等高阶技巧,不定期为你奉上基础数据结构…...

XS2100S:IEEE 802.3af/at 兼容、用电设备接口控制器,集成功率MOSFET V1.0.3
XS2100S:IEEE 802.3af/at 兼容、用电设备接口控制器,集成功率MOSFET V1.0.3 北京冠宇铭通 肖小姐 概述 XS2100S 为用电设备 (PD) 提供符合以太网供电 (PoE)系统 IEEE802.3af/at 标准的完整接口。 XS2100S 为 PD 提供检测信号、分级信号以及带有浪…...

智慧城市如何助力疫情防控:科技赋能城市安全
目录 一、引言 二、智慧城市与疫情防控的紧密结合 三、智慧城市在疫情防控中的具体应用 1、智能监测与预警系统 2、智慧医疗与健康管理 3、智能交通与物流管理 4、智慧社区与基层防控 四、科技赋能城市安全的未来展望 五、结论 一、引言 近年来,全球范围内…...
Chromium内核浏览器编译记(四)Linux版本CEF编译
转载请注明出处:https://blog.csdn.net/kong_gu_you_lan/article/details/136508294 本文出自 容华谢后的博客 0.写在前面 本篇文章是用来记录编译Linux版本CEF的步骤和踩过的坑,以防止后续再用到的时候忘记,同时也希望能够帮助到遇到同样问…...
NextJs教程系列(一):介绍安装
什么是 Next.js Next.js 是一个用于构建全栈 Web 应用程序的 React 框架。您可以使用 React 组件来构建用户界面,并使用 Next.js 来构建其他功能和优化。 Next.js 的特点 构建全栈 Web 应用程序的 React 框架。为 React 提供了开箱即用的服务器端渲染。为 React …...
python界面开发 - Menu (popupmenu) 右键菜单
文章目录 1. python图形界面开发1.1. Python图形界面开发——Tkinter1.2. Python图形界面开发——PyQt1.3. Python图形界面开发——wxPython1.4. Python图形界面开发—— PyGTK:基于GTK1.5. Python图形界面开发—— Kivy1.6. Python图形界面开发——可视化工具1.7. …...
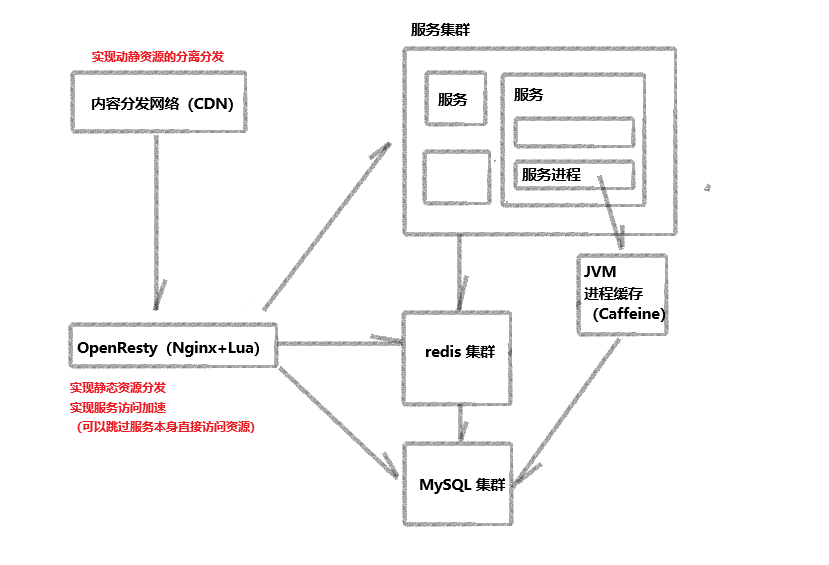
微服务架构 | 多级缓存
INDEX 通用设计概述2 优势3 最佳实践 通用设计概述 通用设计思路如下图 内容分发网络(CDN) 可以理解为一些服务器的副本,这些副本服务器可以广泛的部署在服务器提供服务的区域内,并存有服务器中的一些数据。 用户访问原始服务器…...
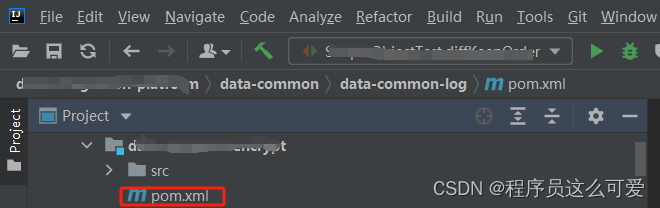
怎么将pom在文件放到src下方
今天在IDEA从git拉取项目的时候,发现pom.xml文件在文件夹src的上方,平时看惯了项目的pom.xml文件在文件夹src的下方,应该怎么去设置呢? 点击设置——>点击Folder Always on Top 即可 参考:http://t.csdnimg.cn/s34…...

浅谈网络爬虫与Web安全
网络爬虫(Web Crawler),又称网络蜘蛛(Web Spider)或网络机器人(Web Robot),是一种按照一定的规则自动抓取万维网资源的程序或者脚本,已被广泛应用于互联网领域。搜索引擎使用网络爬虫抓取Web网页、文档甚至图片、音频、视频等资源,…...
C++vector的使用方法
文章目录 一、vector的介绍1. 文档链接2. 简要介绍 二、vector的使用1.vector的定义(1)构造函数(2)拷贝构造函数(2)赋值重载 2. vector 增删查改(1)operator [](2&#x…...
视频生成模型Sora的全面解析:从AI绘画、ViT到ViViT、DiT、VDT、NaViT、VideoPoet
视频生成模型Sora的全面解析:从AI绘画、ViT到ViViT、DiT、VDT、NaViT、VideoPoet 真没想到,举例视频生成上一轮的集中爆发才过去三个月,没想OpenAI一出手,该领域又直接变天了自打2.16日OpenAI发布sora以来,不但把同时…...

4.1k star,官方出品的redis桌面管理工具——redislnsight
导航 令人抓狂的大key加载RedisInsight 简介RedisInsight的亮点GitHub 地址安装和使用RedisInsight 下载安装 使用RedisInsight redis数据库可视化直观的CLI(Command-Line Interface)日志分析和命令分析 结语参考 令人抓狂的大key加载 工欲善其事必先利…...
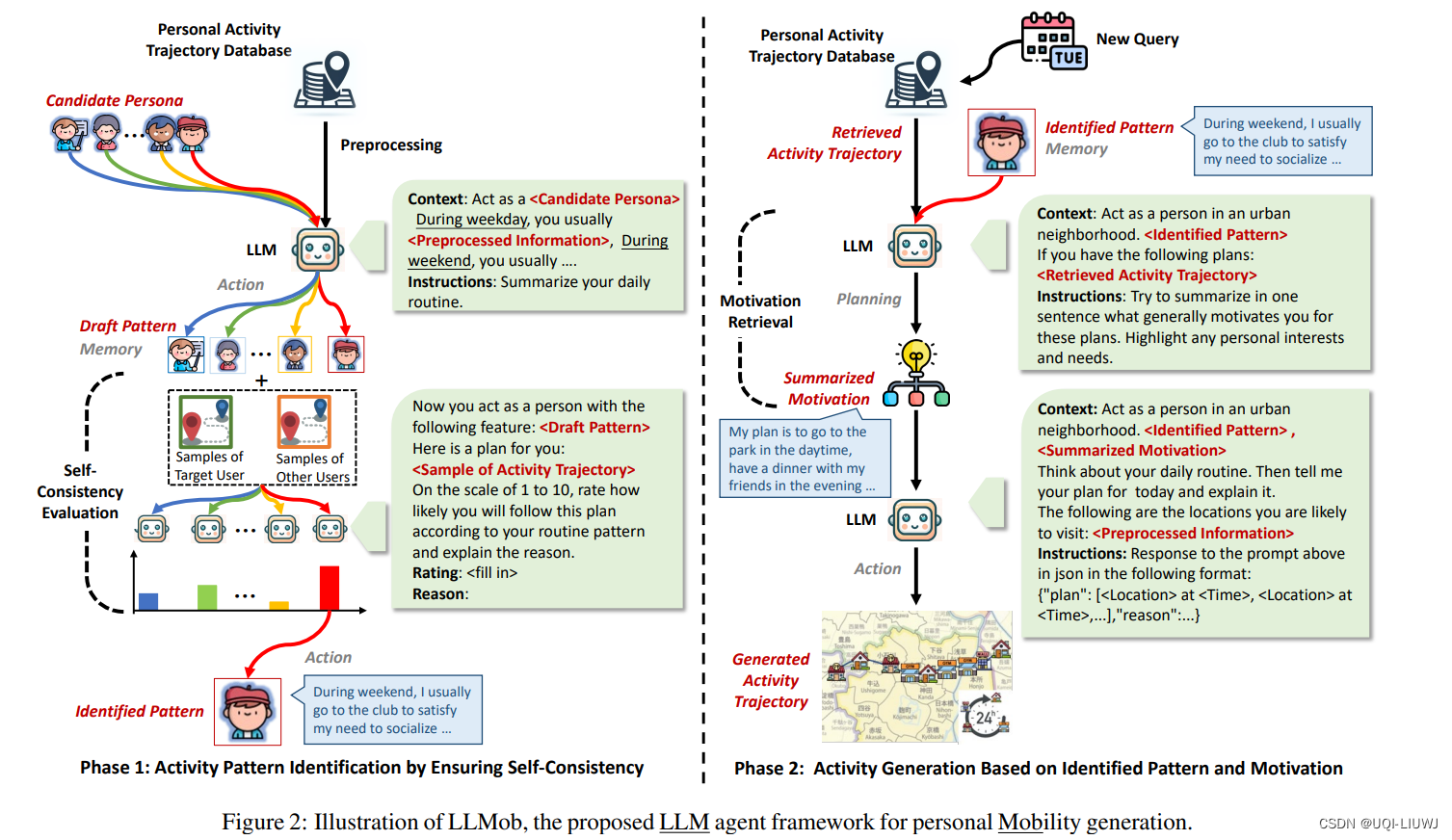
论文目录3:大模型时代(2023+)
1 instruction tuning & in context learning 论文名称来源主要内容Finetuned Language Models Are Zero-Shot Learners2021 机器学习笔记:李宏毅ChatGPT Finetune VS Prompt_UQI-LIUWJ的博客-CSDN博客 早期做instruction tuning的work MetaICL: Learning to …...
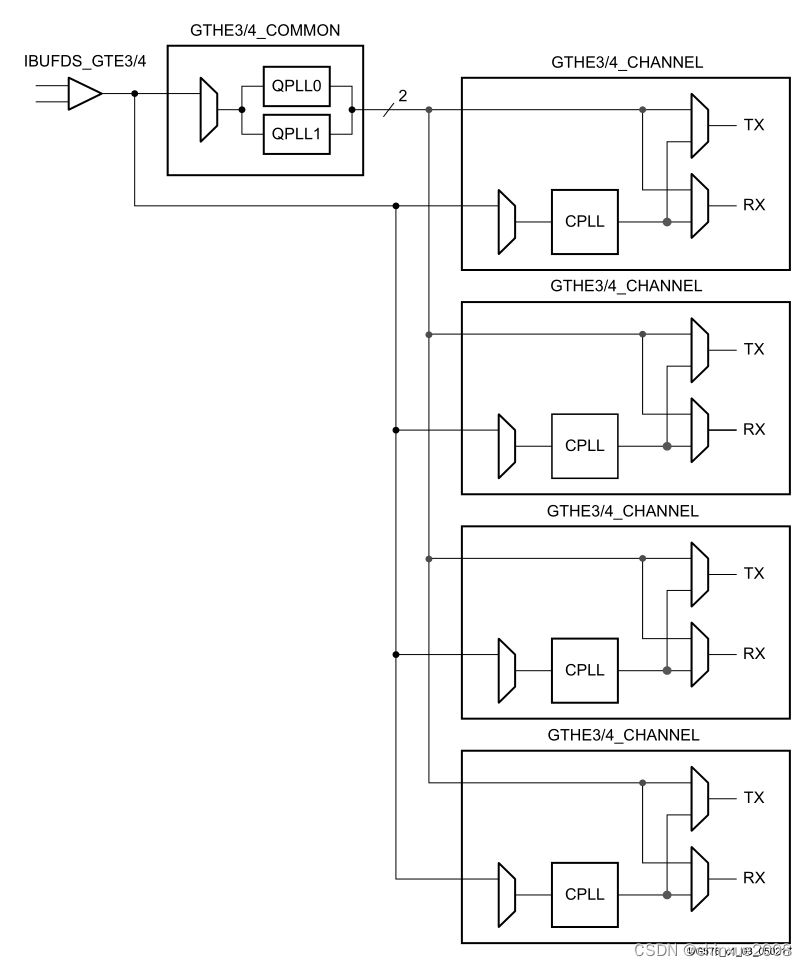
FPGA IBUFG
IBUFG和IBUFGDS的输入端仅仅与芯片的专用全局时钟输入管脚有物理连接,与普通IO和其它内部CLB等没有物理连接。 所以,IBUFG输入的不能直接接另外信号。 GTH transceiver primitives are called GTHE3_COMMON and GTHE3_CHANNEL in UltraScale FPGAs, an…...
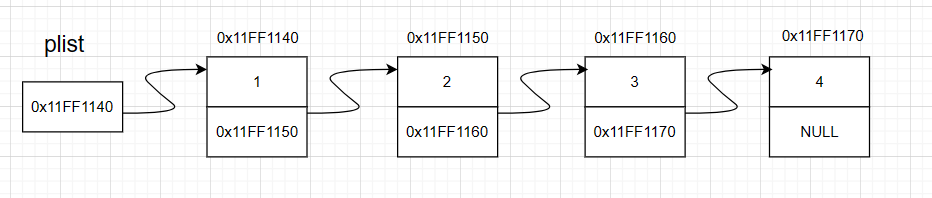
探索数据结构:单链表的实战指南
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:数据结构与算法 贝蒂的主页:Betty‘s blog 前言 在上一章节中我们讲解了数据结构中的顺序表,知道了顺序…...
短视频矩阵系统----矩阵系统源码搭建(技术门槛?)
短视频矩阵是什么意思?短视频矩阵的含义可以理解为全方位的短视频账号,通过不同的账号实现全方位的品牌展示。实际上是指一个短视频账号,通过不同的链接实现品牌展示,在不同的粉丝流量账号中互相转发同一个品牌,在主账…...

Spring事务注解@Transactional的流程和源码分析
Spring事务简介 Spring事务有两种方式: 编程式事务:编程式事务通常使用编程式事务管理API实现,比如Spring提供的PlatformTransactionManager接口,使用它手工编码去操控事务。声明式事务:注解式事务使用AOP࿰…...
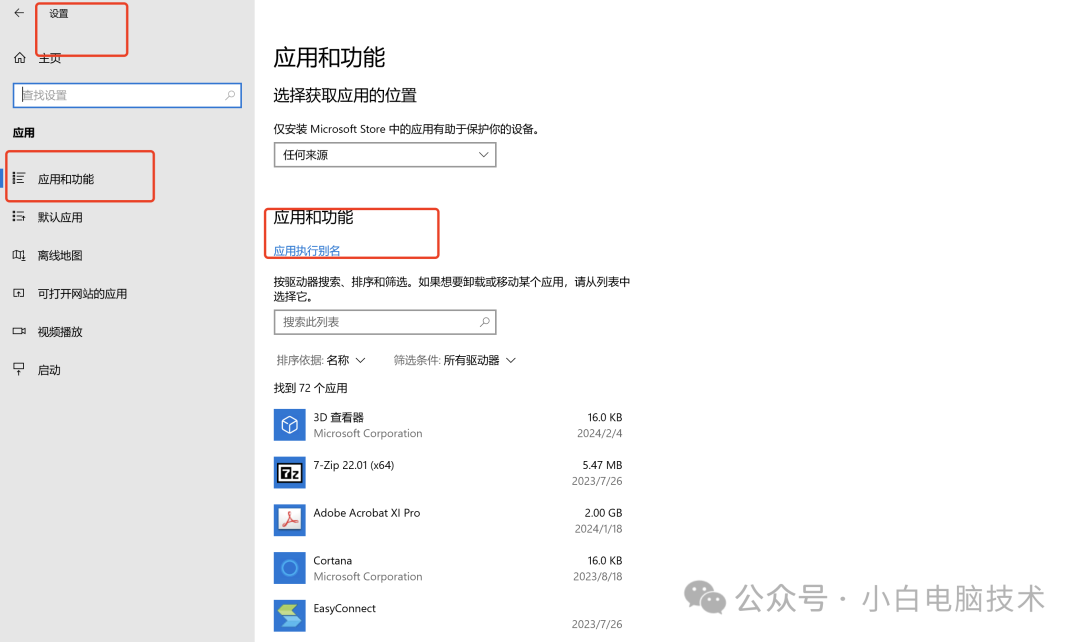
在别的地方下载的二次封装Windows镜像怎么安装?GHO镜像详细安装教程
前言 在系统之家或者其他地方下载的镜像文件怎么装到电脑上? 首先要知道系统之家下载的Windows镜像文件基本上都是.iso结尾的,要进入到对应镜像包才能看出系统镜像是什么格式。 如何分辨镜像的格式 选择对应的.iso镜像,点击【鼠标右键】-【装…...

使用Lerna + Yarn Workspace管理Monorepo项目
1.前言 通常,我们会根据自身业务的实际情况,将通用的组件、逻辑等提取成NPM包,方便以后复用。但这些提取出来的NPM包可能互相之间存在依赖,如果仍然采用 Multirepo 的形式进行管理,则在包的版本管理、依赖管理、调试等…...
读取压缩包文件内容)
如何将gzip后缀压缩包重命名任意后缀名并依然通过gzip.open()读取压缩包文件内容
在 Python 中,gzip.open() 用于解压缩 .gz 后缀的文件。因此,如果您将文件的后缀从 .gz 更改为其他后缀,例如 .diy,然后尝试使用 gzip.open() 打开它,会导致失败,因为 Python 会尝试使用 gzip 解压缩它&…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...