算法->位运算
有关位运算的操作符
>><<&|^~
常见位运算操作
给定一个数,确定它的二进制中第x位是0还是1
(n >> x) & 1;
将一个数n的二进制中第x位修改为1
n |= (1 << x)
将一个数n的二进制中第x位修改为0
n &= (~(1 << x))
提取一个数二进制中最右侧的1
n & (-n)
去掉一个数中二进制最右侧的1
n & (n-1)
异或运算律
- a ^ a = 0
- a ^ 0 = a
- a ^ b ^ c = a ^ (b ^ c)
191. 位1的个数 - 力扣(LeetCode)
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
示例 1:
输入: n = 00000000000000000000000000001011
输出: 3
解释: 输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入: n = 00000000000000000000000010000000
输出: 1
解释: 输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入: n = 11111111111111111111111111111101
输出: 31
解释: 输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
解题思路
n & (n-1)每次可以干掉二进制中最右侧的1
代码实现
class Solution {
public:int hammingWeight(uint32_t n) {int ret = 0;while(n != 0){n &= n-1;ret++;}return ret;}
};
338. 比特位计数 - 力扣(LeetCode)
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入: n = 2
输出: [0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
示例 2:
输入: n = 5
输出: [0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
解题思路
利用n&(n-1)从最高位开始统计位1的个数,将结果存放到vector中即可。时间复杂度O(n^2)
代码实现
class Solution
{
public:vector<int> countBits(int n) {vector<int> ans(n+1);while(n >= 0){int ret = 0,tmp = n;while(tmp != 0){tmp = tmp & (tmp-1);ret++;}ans[n--] = ret;}return ans;}
};
461. 汉明距离 - 力扣(LeetCode)
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
输入: x = 1, y = 4
输出: 2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
解题思路
异或后求二进制位1的个数即可
代码实现
class Solution
{
public:int hammingDistance(int x, int y) {//异或,求异或后二进制1的个数即可int ret = x ^ y;int sum = 0;while(ret != 0){ ret &= (ret-1);sum++;}return sum;}
};
136. 只出现一次的数字 - 力扣(LeetCode)
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入: nums = [2,2,1]
输出: 1
示例 2 :
输入: nums = [4,1,2,1,2]
输出: 4
示例 3 :
输入: nums = [1]
输出: 1
解题思路
- a^0 = a;
- a^a = 0;
- abc = a(bc)
- 41212 = 4(11)(22)
- 空间复杂度要求O(n) 不能使用哈希表
代码实现
class Solution
{
public:int singleNumber(vector<int>& nums) {//a^0 = a;//a^a = 0;//a^b^c = a^(b^c)//4^1^2^1^2 = 4^(1^1)^(2^2)int ret = 0;for(auto &e : nums){ret ^= e;}return ret;}
};
面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode)
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:
输入: s = "leetcode"
输出: false
示例 2:
输入: s = "abc"
输出: true
限制:
0 <= len(s) <= 100s[i]仅包含小写字母- 如果你不使用额外的数据结构,会很加分。
解题思路
- 哈希表。
- 字符串中仅包含小写字母,使用数组模拟哈希表即可。时间复杂度O(n);
- 位运算
- 位图思想 26个比特位即可(一个字节即可)
代码实现
class Solution
{
public:bool isUnique(string astr) {if(astr.size() > 26){return false;}//哈希表// int hash[26] = {0};// for(size_t i = 0; i < astr.size(); ++i)// {// hash[astr[i] - 'a']++;// }// for(auto e : hash)// {// if(e >= 2 ) return false;// }// return true;// 位图int bit_map = 0;for(auto e : astr){int index = e - 'a';//判断是否在位图中。if((bit_map >> index) & 1 == 1) return false;//加入位图bit_map |= (1 << index);}return true;}
};
268. 丢失的数字 - 力扣(LeetCode)
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入: nums = [3,0,1]
输出: 2
解释: n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入: nums = [0,1]
输出: 2
解释: n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入: nums = [9,6,4,2,3,5,7,0,1]
输出: 8
解释: n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入: nums = [0]
输出: 1
解释: n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
解题思路
- 哈希表
- 高斯求和
- 异或运算符
class Solution
{
public:int missingNumber(vector<int>& nums) {//哈希表// int hash[10000] = {0};// //存放到哈希表中// for(size_t i = 0; i < nums.size();++i)// {// hash[nums[i]]++;// }// //遍历哈希表// for(size_t i =0 ; i < 10000; i++)// {// if(hash[i] ==0 ) return i;// }// return 0;//高斯求和// size_t n = nums.size();// int sum = 0;// for(size_t i = 0; i < n ; ++i)// {// sum += nums[i];// }// return ((n) * (n +1) / 2 ) - sum;//位运算(异或运算律)int ret = 0;for(auto e : nums){ret ^= e;}for(int i = 0; i < nums.size() + 1 ; ++i){ret ^= i;}return ret;}};
相关文章:

算法->位运算
有关位运算的操作符 >> <<&|^~ 常见位运算操作 给定一个数,确定它的二进制中第x位是0还是1 (n >> x) & 1; 将一个数n的二进制中第x位修改为1 n | (1 << x) 将一个数n的二进制中第x位修改为0 n & (~(1 << x)) 提…...

【Python】成功解决ModuleNotFoundError: No module named ‘matplotlib‘
【Python】成功解决ModuleNotFoundError: No module named ‘matplotlib’ 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程👈…...

centos7中python3.10找不到openssl解决方案
如果有用其他方法安装了其他版本openssl,记得卸载其他的openssl,删除其他的openssl相关文件。 yum remove openssl* rm -rf ***下载最新版的openssl文件 按照官网安装方法安装openssl 官方安装地址https://docs.python.org/3/using/unix.html#on-linu…...

【Spring Boot `@Autowired` Annotation】
文章目录 1. 使用Qualifier注解2. 使用Primary注解3. 手动注入(较少推荐) 在Spring Boot中,Autowired注解用于自动装配bean。默认情况下,它按照类型进行装配。当存在多个相同类型的bean时,就会出现以下错误:…...
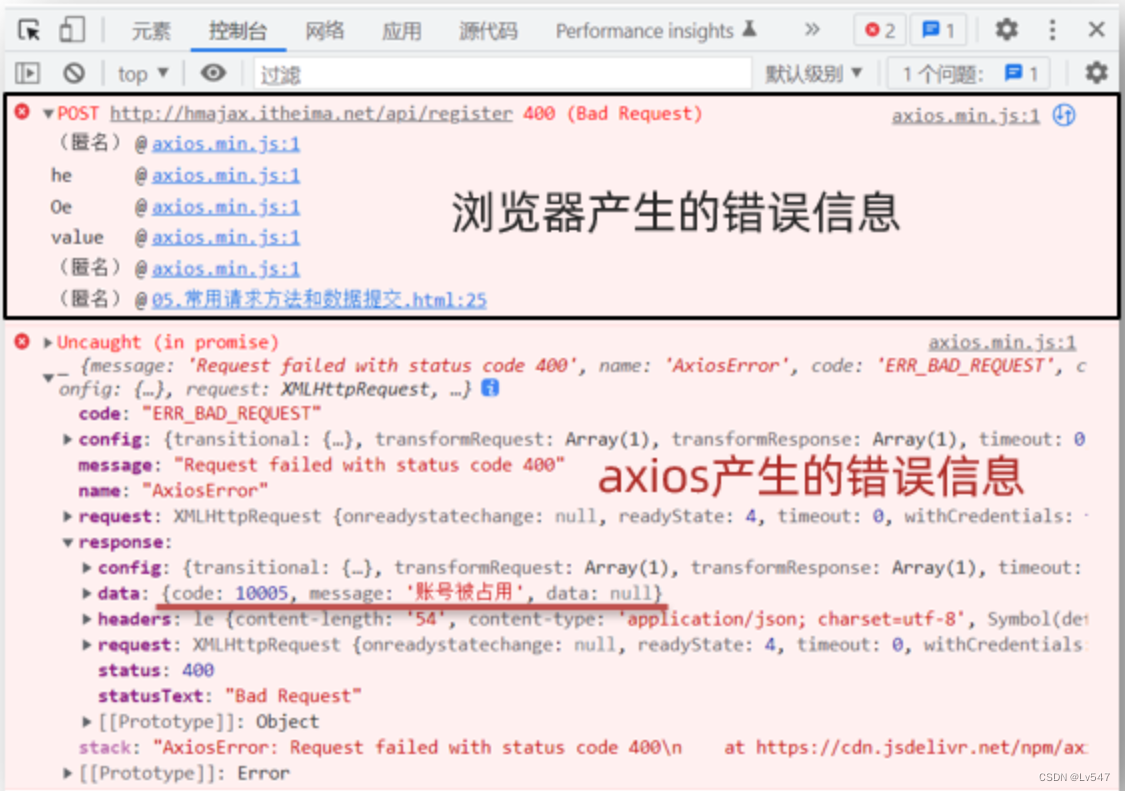
03.axios数据提交和错误处理
一.axios常用请求方法和数据提交 1. 想要提交数据,先来了解什么是请求方法 请求方法是一些固定单词的英文,例如:GET,POST,PUT,DELETE,PATCH(这些都是http协议规定的)&am…...
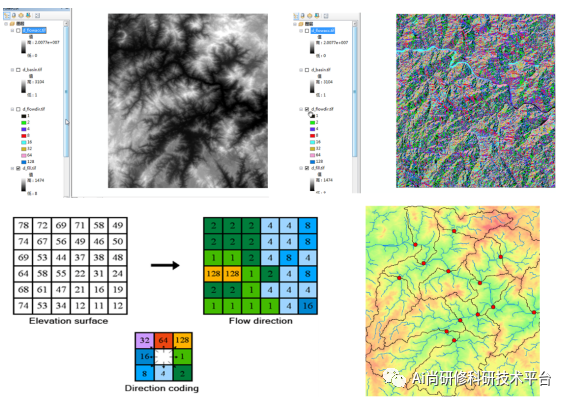
无人机生态环境监测、图像处理与GIS数据分析
构建“天空地”一体化监测体系是新形势下生态、环境、水文、农业、林业、气象等资源环境领域的重大需求,无人机生态环境监测在一体化监测体系中扮演着极其重要的角色。通过无人机航空遥感技术可以实现对地表空间要素的立体观测,获取丰富多样的地理空间数…...

centos7.9升级ssh和openssl
一、环境 [roottmp179 package]# ssh -V OpenSSH_7.4p1, OpenSSL 1.0.2k-fips 26 Jan 2017 [roottmp179 package]# cat /etc/redhat-release CentOS Linux release 7.9.2009 (Core) 二、 升级前准备 mkdir /opt/package cd /opt/package wget https://www.openssl.org/source…...
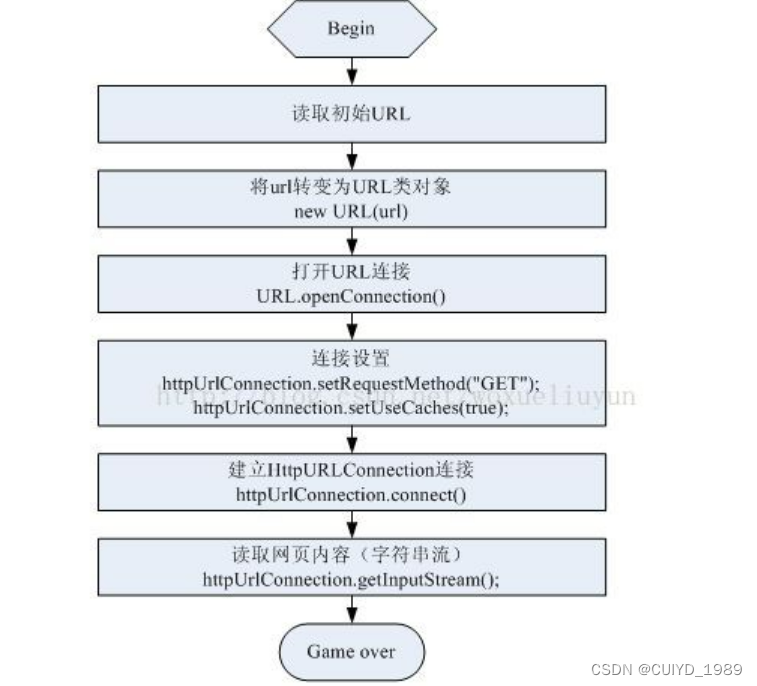
HttpURLConnection详解及使用
HttpURLConnection 请求响应流程 设置连接参数的方法 setAllowUserInteractionsetDoInputsetDoOutputsetIfModifiedSincesetUseCachessetDefaultAllowUserInteractionsetDefaultUseCaches 发送URL请求 建立实际连接之后,就是发送请求,把请求参数传到…...

npm下载时下载失败解决方法
1.清楚缓存 npm cache clean --force2.切换下载镜像 1.查看当前使用的镜像地址命令 npm config get registry切换为淘宝镜像命令(安装一些package容易报错) npm config set registry https://registry.npm.taobao.org或官方: npm config…...

Python实战:浅析Python输入输出理解数据交换的基本原理
在Python编程中,输入输出是数据交换的基础。本文将深入探讨Python中的输入输出功能,包括标准输入输出、文件输入输出、格式化输出等。我们将通过具体的代码示例来展示如何使用Python进行数据输入和输出,并理解其背后的工作原理。 1. 标准输入…...

MySQL--explain执行计划详解
什么是执行计划? SQL的执行计划,通俗来说就是SQL的执行情况,一条SQL语句扫描哪些表,那个子查询先执行,是否用到了索引等等,只有当我们知道了这些情况之后才知道,才可以更好的去优化SQL…...
)
【NERF】入门学习整理(一)
【NERF】入门学习整理 1. 【NERF】入门学习整理1.1 基础含义输入输出2.位置编码含义3.代码中实际网路结构4.Volume Render部分(64个采样点处理)5.Volume Render部分(64个采样点处理)【NERF】及其变种(二) 1. 【NERF】入门学习整理 1.1 基础含义输入输出 深度学习模型中…...

基于ZYNQ PS-SPI的Flash驱动开发
本文使用PS-SPI实现Flash读写,PS-SPI的基础资料参考Xilinx UG1085的文档说明,其基础使用方法是,配置SPI模式,控制TXFIFO/RXFIFO,ZYNQ的IP自动完成发送TXFIFO数据,接收数据到RXFIFO,FIFO深度为12…...

Linux Shell:local关键字
Linux Shell:local关键字 在 Bash 中,local 是一个用于声明局部变量的关键字。当在函数内部使用 local 声明变量时,该变量只能在函数内部使用,并且不会对函数外部的同名变量产生影响。这样可以确保在函数内部定义的变量不会意外地…...

如何开发python毕业设计
开发Python毕业设计需要以下步骤: 选择项目主题: 选择一个与你的兴趣和专业相关的主题。确保主题具有一定的挑战性,但又不至于过于复杂,以确保你能够在规定时间内完成项目。 制定项目计划: 制定一个清晰的项目计划&…...
D*算法超详解 (D星算法 / Dynamic A*算法/ Dstar算法)(死循环解决--跟其他资料不一样奥)
所需先验知识(没有先验知识可能会有大碍,了解的话会对D*的理解有帮助):A*算法/ Dijkstra算法 何为D*算法 Dijkstra算法是无启发的寻找图中两节点的最短连接路径的算法,A*算法则是在Dijkstra算法的基础上加入了启发函数…...
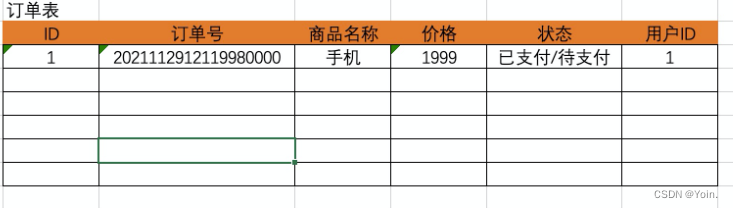
django学习记录07——订单案例(复选框+ajax请求)
1.订单的数据表 1.1 数据表结构 1.2 数据表的创建 models.py class Order(models.Model):"""订单号"""oid models.CharField(max_length64, verbose_name"订单号")title models.CharField(max_length64, verbose_name"名称&…...

Qt 定时器事件
文章目录 1 定时器事件1.1 界面布局1.2 关联信号槽1.3 重写timerEvent1.4 实现槽函数 启动定时器 2 定时器类 项目完整的源代码 QT中使用定时器,有两种方式: 定时器类:QTimer定时器事件:QEvent::Timer,对应的子类是QTi…...

LLM 推理优化探微 (2) :Transformer 模型 KV 缓存技术详解
编者按:随着 LLM 赋能越来越多需要实时决策和响应的应用场景,以及用户体验不佳、成本过高、资源受限等问题的出现,大模型高效推理已成为一个重要的研究课题。为此,Baihai IDP 推出 Pierre Lienhart 的系列文章,从多个维…...
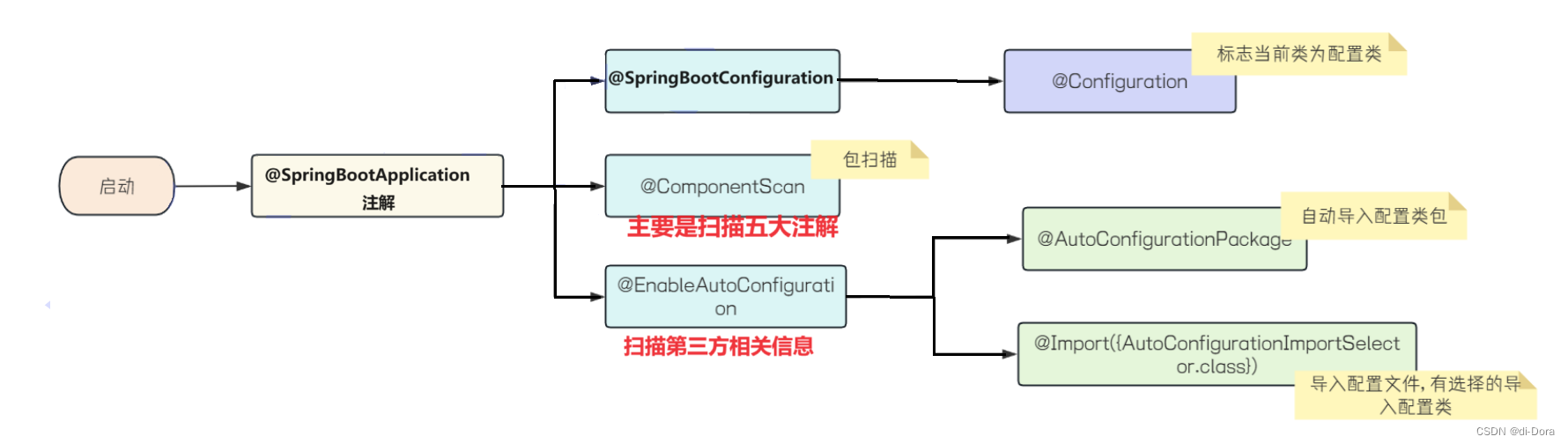
JavaEE进阶(15)Spring原理:Bean的作用域、Bean的生命周期、Spring Boot自动配置(加载Bean、SpringBoot原理分析)
接上次博客:JavaEE进阶(14)Linux基本使用和程序部署(博客系统部署)-CSDN博客 目录 关于Bean的作用域 概念 Bean的作用域 Bean的生命周期 源码阅读 Spring Boot自动配置 Spring 加载Bean 问题描述 原因分析 …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
