Redis的HyperLogLog原理介绍
Redis 的 HyperLogLog 数据结构实现了一种基于概率的基数估算算法,用于在占用极小内存的情况下估算一个集合中不重复元素(唯一值)的数量。以下是 HyperLogLog 算法的基本原理:
-
哈希函数:
- HyperLogLog 使用一个强散列函数将输入的元素映射为固定长度的二进制串。
-
位前导零统计:
- 对每个元素经过哈希后的二进制串,统计从最高位开始连续零的个数(即前导零个数)。这个值反映了元素哈希值的稀有程度,间接表示了元素的独特性。
-
存储与计数:
- Redis 中的 HyperLogLog 结构内部维护了一个大小固定的桶数组,默认大小为 2^14 = 16384 个桶。
- 每个桶用于存储对应的元素哈希值所观察到的最大前导零个数。
- 当添加新的元素时,它会被哈希并找到对应的桶来更新该桶中的最大前导零计数值。
-
基数估算:
- 利用统计的所有桶中最长的前导零序列,通过预定义的公式计算出一个近似的基数(唯一元素数量),这个估算值通常会非常接近实际基数,但不是精确值。
- 标准误差大约是 0.81%,这意味着对于大量数据,HyperLogLog 能够以相对较小的误差估计基数。
-
空间效率:
- 即使可以处理多达 2^64 个不同的元素,Redis 中单个 HyperLogLog 键只需要大约 12KB 的固定内存空间。
- 在初始阶段或基数较小的时候,HyperLogLog 使用稀疏存储模式,随着基数增加,当满足一定条件后会转换为稠密存储模式,即上述的固定大小的桶数组。
-
合并操作:
- HyperLogLog 还支持多个集合的合并操作(
pfmerge命令),允许将多个 HyperLogLog 键合并成一个新的键,同时正确估算所有源键包含的唯一元素总数,这对于分布式环境下的基数统计尤为有用。
- HyperLogLog 还支持多个集合的合并操作(
总之,HyperLogLog 是一种高效的空间优化型算法,适合于在有限资源下进行大规模数据集的去重计数任务。
Redis 的 HyperLogLog 原理可以用一个简单的比喻来通俗易懂地解释:
想象一下你在一个巨大的、无限大的公园里随机扔硬币。每次扔出的硬币落地时,我们只关心它正面朝上还是反面朝上,并且记录下第一次出现正面朝上的次数(比如,扔了5次才见到第一个正面,就记为5)。由于硬币是随机的,这个“第一次正面”的次数与公园中人的数量有一定的关系:人越多,每个区域平均需要扔更多次才能看到正面的概率越大。
HyperLogLog 就像是这样一种神奇的计数器,不过它不是真的扔硬币,而是对输入元素(如用户ID、网页访问等)进行哈希处理,将这些元素映射到一个很大的虚拟空间内,就好比在不同的区域内扔硬币。每个哈希值对应的就是一次“扔硬币”,而观察到的最长连续零位(前导零个数)就代表了需要多少次“扔”才能见到“正面”。
在 Redis 中,HyperLogLog 用一个固定大小的桶数组(默认大小为2^14个桶)来存储各个桶对应的最长前导零个数。通过统计所有桶中的最大前导零计数值,并结合一个数学公式,就可以估算出不重复元素的大致数量,尽管实际上并没有存储每个具体的唯一元素。
所以,虽然 HyperLogLog 不会记住每一个独特的元素,但它能用极小的空间开销(仅需约12KB),相对准确地估计高达2^64个不同元素的数量。当然,这是一种概率算法,因此结果存在一定的误差,但其标准误差率相当低,在0.81%左右。
HyperLogLog 在实际开发中主要用于需要统计大量唯一值数量但又对内存占用敏感的场景,它可以提供一个非常接近真实基数的估算值,同时占用极小的存储空间。以下是一些具体的应用场景:
-
网站独立访客(UV)统计:
- 通过记录用户访问时的标识符(如 IP 地址、Cookie 或用户ID),使用 HyperLogLog 进行去重计数,可以快速估算一天内或一段时间内的独立访客数量。
-
广告点击独立用户统计:
- 在在线广告系统中,为了评估广告效果,需要统计每个广告被多少不同的用户点击过。HyperLogLog 可以用来估算每条广告的独立点击用户数。
-
社交网络分析:
- 社交网络中的粉丝数、关注数等指标可以通过 HyperLogLog 来进行估算,尤其是在大数据量下不需要知道具体的粉丝列表,只需估计大致的数量。
-
实时事件流处理:
- 对于日志收集和分析平台,HyperLogLog 可用于实时统计每天或每小时发生的不同类型的事件数量,例如异常请求次数、不同设备型号的活跃用户数等。
-
数据库索引优化:
- 在数据导入预处理阶段,可利用 HyperLogLog 预估某个字段的唯一值数量,以便更准确地选择合适的索引策略。
-
分布式环境下的去重计算:
- 在分布式系统中,数据可能分布在多个节点上。每个节点本地维护一个 HyperLogLog 结构,然后通过
pfmerge命令将各个节点的 HyperLogLog 合并,最终得到全系统的唯一值数量。
- 在分布式系统中,数据可能分布在多个节点上。每个节点本地维护一个 HyperLogLog 结构,然后通过
总之,只要涉及到在海量数据下高效估算唯一元素数量的需求,都可能是 HyperLogLog 大显身手的地方。
相关文章:

Redis的HyperLogLog原理介绍
Redis 的 HyperLogLog 数据结构实现了一种基于概率的基数估算算法,用于在占用极小内存的情况下估算一个集合中不重复元素(唯一值)的数量。以下是 HyperLogLog 算法的基本原理: 哈希函数: HyperLogLog 使用一个强散列函…...

微信小程序开发系列(二十六)·小程序运行机制(启动、前后台状态、挂起、销毁)和小程序更新机制
目录 1. 小程序运行机制 1.1 启动 1.2 前台和后台状态 1.3 挂起 1.4 销毁 2. 小程序更新机制 1. 小程序运行机制 1.1 启动 小程序启动可以分为两种情况,一种是冷启动,一种是热启动。 冷启动:如果用户首次打开,或小…...

百度信息流
计划: 流量选择 - 四个维度: 百度信息流 ; 整合了百度APP、WAP、PC各频道信息流和内容详情页的流量资源,广告和信息流内容资讯穿插展现;适合所有产品呢 好看视频; 汇集海量优质的视频内容,通过智能推荐算法为用户推送最适合的视频广告,视频广告在列表页有声…...
——设计模式)
JAVA后端开发面试基础知识(十)——设计模式
创建型模式 创建型模式的作用就是创建对象,说到创建一个对象,最熟悉的就是 new 一个对象,然后 set 相关属性。但是,在很多场景下,我们需要给客户端提供更加友好的创建对象的方式,尤其是那种我们定义了类&am…...

红帽认证知识储备-Linux安全
Linux安全 内置安全机制 常见的系统用的centos中用的是SELinux,ubuntu用的是AppArmor,deepin什么都没用 SELINUX 定义 SELinux 是一个 Linux 内核安全模块,它增强了系统的安全性,通过实施强制访问控制策略来限制程序和用户对系…...

Rust 语言中的 dyn 关键字
在 Rust 中,&dyn Error 是一个指向动态类型的 Error trait 对象的引用。这里的 dyn 关键字用于表示一个动态分派的 trait 对象。动态分派允许你在运行时确定实际的对象类型,而不是在编译时。 dyn 关键字在 Rust 中用于替换早期版本中的 & 符号&…...
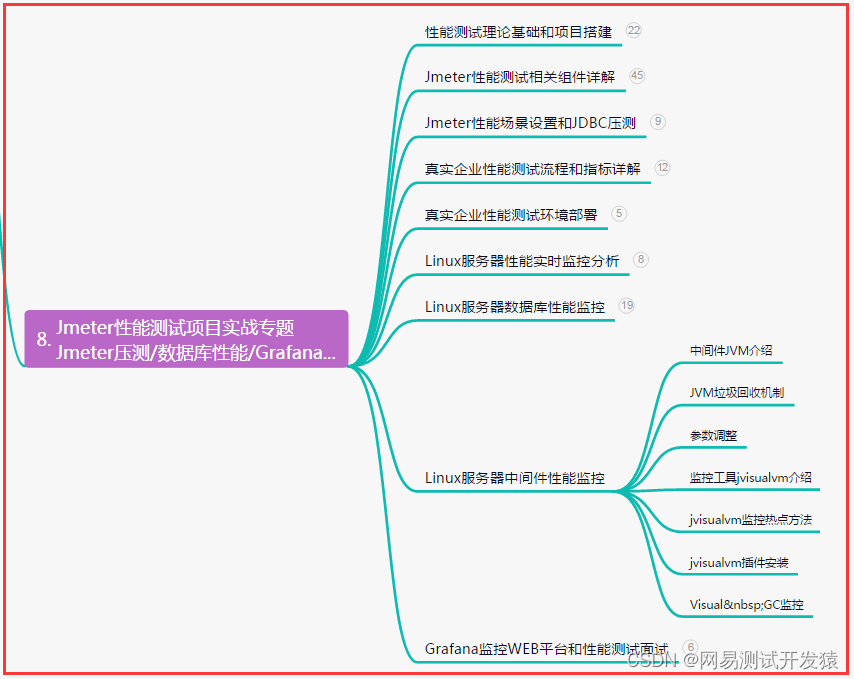
软件测试实战,Web项目网页bug定位详细分析总结(详全)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、前置条件 1&a…...

清除Mac OS上Xcode占用的空间
最近自己的Mac OS存储空间严重不足,想了一下,大概是从安装 Xcode 之后出现,在系统下通过 du 命令分析各目录大小,发现大概下面几个目录占用空间比较大,所以针对这几个名目录作了一下清理,释放了几十个G的空…...

开源的Java图片处理库介绍
在 Java 生态系统中,有几个流行的开源库可以用于图片处理。这些库提供了丰富的功能,如图像缩放、裁剪、颜色调整、格式转换等。以下是几个常用的 Java 图片处理库的介绍,包括它们的核心类、主要作用和应用场景,以及一些简单的例子…...
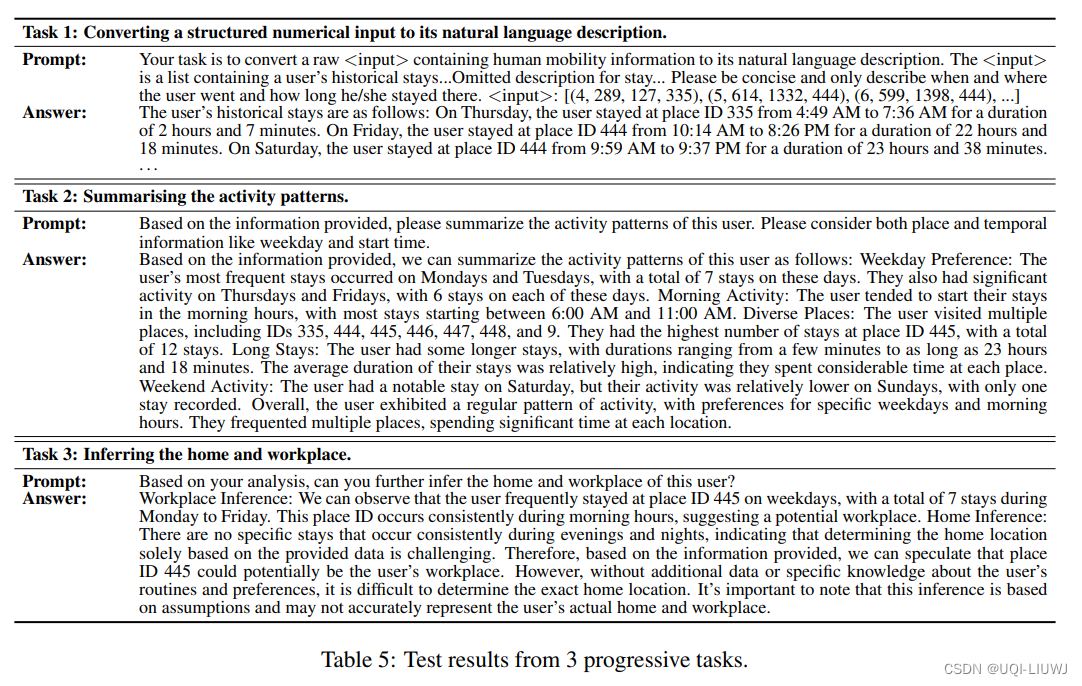
论文笔记 Where Would I Go Next? Large Language Models as Human Mobility Predictor
arxiv 2023 08的论文 1 intro 1.1 人类流动性的独特性 人类流动性的独特特性在于其固有的规律性、随机性以及复杂的时空依赖性 ——>准确预测人们的行踪变得困难近期的研究利用深度学习模型的时空建模能力实现了更好的预测性能 但准确性仍然不足,且产生的结果…...
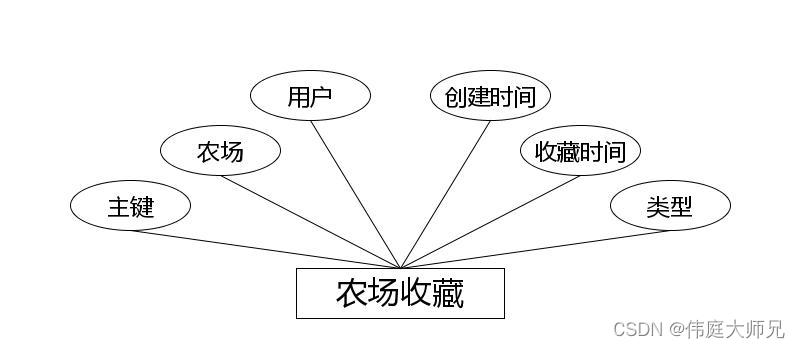
农场管理小程序|基于微信小程序的农场管理系统设计与实现(源码+数据库+文档)
农场管理小程序目录 目录 基于微信小程序的农场管理系统设计与实现 一、前言 二、系统设计 三、系统功能设计 1、用户信息管理 2、农场信息管理 3、公告信息管理 4、论坛信息管理 四、数据库设计 五、核心代码 七、最新计算机毕设选题推荐 八、源码获取&#x…...
【前端】vscode快捷键和实用Api整理
vscode的快捷键 创建a.html 生成模板 !回车 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" …...

抖音商家活动信息未在商详展示会有哪些处罚?
一、什么是「违规玩法-活动信息未在商详展示」? 什么是「违规玩法-活动信息未在商详展示」?由于当前平台未提供官方营销工具(例如免单、返现等),但是创作者在进行商品推广(不仅限口播、画面、标题文案等)宣传该类营销玩法,未在商品商详页展示说明&…...

智慧公厕方案_智慧公厕解决方案_智慧公厕整体解决方案
一、什么是智慧公厕? 在现代城市化进程中,公共厕所是不可或缺的基础设施之一。然而,传统的公厕管理模式已经无法满足市民对高效、便捷厕所服务的需求。为了实现公共厕所的信息化管理,智慧公厕整体解决方案应运而生。智慧公厕具体…...

【Python】成功解决IndexError: list index out of range
【Python】成功解决IndexError: list index out of range 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程👈 希望得到您的订…...
=E(X)E(Y))
对于两个独立随机变量X,Y, E(XY)=E(X)E(Y)
两个独立随机变量X,Y的期望分别是E(X), E(Y), 其乘积XY的期望是多少? 我们可以利用期望的性质来求得XY的期望。由于X、Y是独立随机变量,因此它们的协方差为0,即: cov(X, Y) E(XY) - E(X)E(Y) 0 因此, …...

以题为例 浅谈前缀和算法
前缀求和算法是什么 前缀和算法就是以空间去换取时间,可用于快速求数组的区间和,它可以用于一维数组和二维数组,但我现在只接触了一维数组并没有接触二维数组,所以在这里先介绍一维数组前缀和相关的知识 前缀和典型代码 for(int…...

【Python】进阶学习:OpenCV--一文详解cv2.namedWindow()
【Python】进阶学习:OpenCV–一文详解cv2.namedWindow() 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程👈 希望…...

【嵌入式】字体极限瘦身术:Fontmin在嵌入式UI中的魔法应用(附3500常用汉字)
🧑 作者简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟。提供嵌入式方向的学习指导、简历面…...

蓝桥杯递推与递归法|斐波那契数列|数字三角形|42点问题|数的计算|数的划分(C++)
递归是用来做dfs,是搜索算法的基础 递推是用来做dp部分,及部分其他算法,复杂度较低,不会出现爆栈问题递推法: 递推法是一种在数学和其他领域广泛应用的重要方法,它在计算机科学中被用作一种关键的数值求解…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
