【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM
论文地址:https://arxiv.org/pdf/2310.11453.pdf
相关博客
【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM
【自然语言处理】BitNet b1.58:1bit LLM时代
【自然语言处理】【长文本处理】RMT:能处理长度超过一百万token的Transformer
【自然语言处理】【大模型】MPT模型结构源码解析(单机版)
【自然语言处理】【大模型】ChatGLM-6B模型结构代码解析(单机版)
【自然语言处理】【大模型】BLOOM模型结构源码解析(单机版)
一、简介
语言模型的规模不断扩大,这对部署带来了巨大的挑战。本文设计了一种可扩展且稳定的1-bit Transformer架构来实现大语言模型,称为BitNet。具体来说,使用BitLinear作为标准nn的替代品。实验结果表明BitNet能够显著减少存储占用和能力消耗,并且与最先进的8-bit量化和FP16 Transformer能力相当。此外,BitNet也表现出了类似于全精度Transformer的scaling law,这也表明其有潜力在保持效率和性能的同时,能够更加有效的扩展至更大的语言模型。
二、BitNet

BitNet采用与Transformer相同的布局,但是采用BitLinear而不是标准的矩阵乘法,其他组件仍保持高精度。原因如下:(1) 残差连接和Layer Normalization的计算代价对于LLM可以忽略不计;(2) 随着模型增大,QKV变换的计算代价远小于投影;(3) 保留输入/输出嵌入层的精度,因为语言模型必须使用高精度来执行采样。
1. BitLinear
在二值化前将权重中心化为0均值来增加有限数值范围的容量,然后使用sign函数将权重二值化为+1或-1。二值化后使用缩放因子 β \beta β来降低实值权重和二值化权重之间的 l 2 l2 l2误差。因此,二值化权重 W ∈ R n × m W\in\mathcal{R}^{n\times m} W∈Rn×m可以形式化为:
W ~ = Sign ( W − α ) (1) \widetilde{W}=\text{Sign}(W-\alpha) \tag{1} \\ W =Sign(W−α)(1)
Sign ( W i j ) = { + 1 , if W i j > 0 − 1 , if W i j l e q 0 (2) \text{Sign}(W_{ij})=\begin{cases} +1,&&\text{if}\;W_{ij}>0 \\ -1,&&\text{if}\;W_{ij}leq 0 \\ \end{cases} \tag{2} \\ Sign(Wij)={+1,−1,ifWij>0ifWijleq0(2)
α = 1 n m ∑ i j W i j (3) \alpha=\frac{1}{nm}\sum_{ij}W_{ij} \tag{3} \\ α=nm1ij∑Wij(3)
接下来使用absmax将激活量化至b-bit,即乘以 Q b Q_b Qb再除以输入矩阵的最大绝对值,从而将激活缩放至 [ − Q b , Q b ] ( Q b = 2 b − 1 ) [-Q_b,Q_b](Q_b=2^{b-1}) [−Qb,Qb](Qb=2b−1):
x ~ = Quant ( x ) = Clip ( x × Q b γ , − Q b + ϵ , Q b − ϵ ) (4) \tilde{x}=\text{Quant}(x)=\text{Clip}(x\times\frac{Q_b}{\gamma},-Q_b+\epsilon,Q_b-\epsilon) \tag{4}\\ x~=Quant(x)=Clip(x×γQb,−Qb+ϵ,Qb−ϵ)(4)
Clip ( x , a , b ) = max ( a , min ( b , x ) ) , γ = ∥ x ∥ ∞ (5) \text{Clip}(x,a,b)=\max(a,\min(b,x)),\quad\gamma=\parallel x\parallel_\infty \tag{5} \\ Clip(x,a,b)=max(a,min(b,x)),γ=∥x∥∞(5)
其中 ϵ \epsilon ϵ是防止裁剪时溢出的小浮点数。
对于非线性函数之前的激活,通过减去输入中的最小值将其缩放至 [ 0 , Q b ] [0,Q_b] [0,Qb],从而使得所有值均为非负:
x ~ = Quant ( x ) = Clip ( ( x − η ) × Q b γ , ϵ , Q b − ϵ ) , η = min i , j x i j (6) \tilde{x}=\text{Quant}(x)=\text{Clip}((x-\eta)\times\frac{Q_b}{\gamma},\epsilon,Q_b-\epsilon),\quad\eta=\min_{i,j}x_{ij}\tag{6} \\ x~=Quant(x)=Clip((x−η)×γQb,ϵ,Qb−ϵ),η=i,jminxij(6)
本文中将激活量化至8-bit。此外,为了稳定性和效率,在训练期间按张量执行量化,而在推理时则按token执行量化。
基于上面的量化等式,矩阵乘法可以写作:
y = W ~ x ~ (7) y=\widetilde{W}\tilde{x}\tag{7} \\ y=W x~(7)
假设 W W W中的元素和 x x x是独立同分布的。那么,输出 y y y的方差可以估计为:
Var ( y ) = n Var ( w ~ x ~ ) = n E [ w ~ 2 ] E [ x ~ 2 ] = n β 2 E [ x ~ 2 ] ≈ E [ x ~ 2 ] \begin{align} \text{Var}(y)&=n\text{Var}(\tilde{w}\tilde{x}) \tag*{(8)} \\ &=nE[\tilde{w}^2]E[\tilde{x}^2] \tag*{(9)} \\ &=n\beta^2E[\tilde{x}^2]\approx E[\tilde{x}^2] \tag*{(10)} \end{align} \\ Var(y)=nVar(w~x~)=nE[w~2]E[x~2]=nβ2E[x~2]≈E[x~2](8)(9)(10)
对于全精度计算,若使用标准数据化方法,输出方差 Var ( y ) \text{Var}(y) Var(y)则为1,对于训练稳定性有益。为了在量化后保持方差,在激活量化前引入了LayerNorm函数。这样,输出 y y y的方差估计为 Var ( y ) ≈ E [ LN ( x ~ ) 2 ] = 1 \text{Var}(y)\approx E[\text{LN}(\tilde{x})^2]=1 Var(y)≈E[LN(x~)2]=1,其大小与全精度 Var ( y ) \text{Var}(y) Var(y)是相同量级。在标准的Transformer中,这种方式称为SubLN。利用SubLN和上述量化方法,得到BitLinear:
y = W ~ x ~ = W ~ Quant ( LN ( x ) ) × β γ Q b (11) y=\widetilde{W}\tilde{x}=\widetilde{W}\text{Quant}(\text{LN}(x))\times\frac{\beta\gamma}{Q_b}\tag{11} \\ y=W x~=W Quant(LN(x))×Qbβγ(11)
LN ( x ) = x − E ( x ) Var ( x ) + ϵ , β = 1 n m ∥ W ∥ 1 (12) \text{LN}(x)=\frac{x-E(x)}{\sqrt{\text{Var}(x)+\epsilon}},\quad\beta=\frac{1}{nm}\parallel W\parallel_1 \tag{12} \\ LN(x)=Var(x)+ϵx−E(x),β=nm1∥W∥1(12)
在SubLN操作之后,使用absmax函数对激活进行量化。然后1-bit权重和量化后的激活之间执行矩阵乘法。输出的激活使用 { β , γ } \{\beta,\gamma\} {β,γ}进行重新缩放,从而反量化至原始精度。
基于分组量化和规范化的模型并行。训练大语言模型的一项重要技术是模型并行,其在多个设备上划分矩阵乘法。现有模型并行方法的先决条件是张量在划分维度上是独立的。然而,所有参数 α \alpha α、 β \beta β、 γ \gamma γ和 η \eta η是从整个张量计算出来的,打破了独立性条件。为此,本文提出了一种简单且高效的模型并行方案。将权重和激活分为多个组,然后独立地估计每个组的参数。通过这种方式,可以在不需要额外通信的情况下本地计算这些参数。这种方法称为分组量化(Group Quantization),形式化为:
对于权重矩阵 W ∈ R n × m W\in\mathcal{R}^{n\times m} W∈Rn×m,将其沿着划分维度分为 G G G组,每个组的尺寸为 n G × m \frac{n}{G}\times m Gn×m。我们独立的估计每个组的参数:
α g = G n m ∑ i j W i j ( g ) , β g = G n m ∥ W ( g ) ∥ 1 (13) \alpha_g=\frac{G}{nm}\sum_{ij}W_{ij}^{(g)},\quad\beta_g=\frac{G}{nm}\parallel W^{(g)}\parallel_1 \tag{13} \\ αg=nmGij∑Wij(g),βg=nmG∥W(g)∥1(13)
其中 W ( g ) W^{(g)} W(g)是第 g g g个组的权重矩阵。类似地,对于激活,我们能将输入矩阵 x ∈ R n × m x\in\mathcal{R}^{n\times m} x∈Rn×m划分为 G G G组,每个组计算参数
γ g = ∥ x ( g ) ∥ ∞ , η g = min i j x i j ( g ) (14) \gamma_g=\parallel x^{(g)}\parallel_\infty,\quad\eta_g=\min_{ij}x_{ij}^{(g)}\tag{14} \\ γg=∥x(g)∥∞,ηg=ijminxij(g)(14)
对于LN,应用分组规范化(Group Normalization)技术来计算均值和方差:
LN ( x ( g ) ) = x ( g ) − E ( x ( g ) ) Var ( x ( g ) ) + ϵ (15) \text{LN}(x^{(g)})=\frac{x^{(g)}-E(x^{(g)})}{\sqrt{\text{Var}(x^{(g)})+\epsilon}} \tag{15} \\ LN(x(g))=Var(x(g))+ϵx(g)−E(x(g))(15)
通过分组量化和归一化能有效地实现模型并行,且不需要额外的通信。
2. 模型训练
直通估计器(Straight-through estimator, STE)。为了能够训练1-bit模型利用STE来在反向传播过程中近似梯度。该方法在反向传播过程中会绕开Sign或者Clip这样的不可微函数。因此,STE允许梯度在网络中流动而不受这些不可微函数的影响,使得训练量化模型成为可能。
混合精度训练。虽然权重和激活被量化为低精度,但是梯度和优化器状态仍然是按高精度存储,从而确保训练稳定性和准确率。遵循先前的工作,我们为可学习参数保持高精度格式的潜在权重,以累计参数更新。潜在权重在前向传播过程中被动态二值化,但是不会用在推理过程中。
大学习率。1-bit权重优化的挑战是小的更新量可能不会对权重有任何影响。在训练的开头,这个问题将更加的严重,因此期望模型尽快收敛。为了解决这个问题,探索了各种方法。最终,提高学习率是加速优化最简单且最好的方法。实验表明,大学习率能够使得BitNet很好的收敛,而FP16 Transformer使用大学习率会导致发散。
3. 计算效率
矩阵乘法是大语言模型计算的主要成本,因此这里也仅关注矩阵乘法的计算。
算术操作的能量。不同的算术操作的能量消耗估计如下:
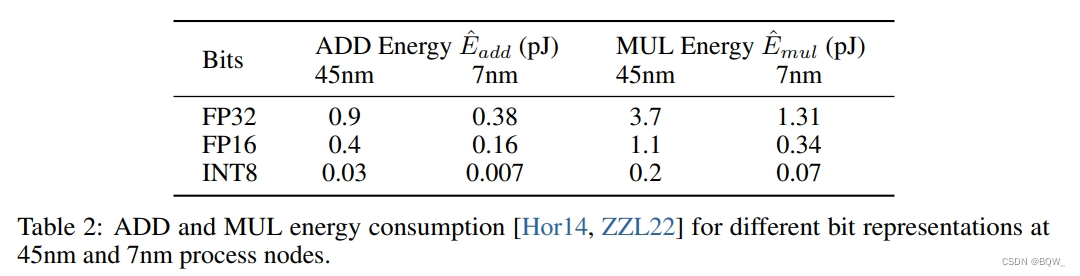
在标准Transformer中,若维度为 m × n m\times n m×n和 n × p n\times p n×p矩阵乘法能量消耗为
E a d d = m × ( n − 1 ) × p × E ^ a d d (16) E_{add}=m\times(n-1)\times p\times\hat{E}_{add} \tag{16} \\ Eadd=m×(n−1)×p×E^add(16)
E m u l = m × n × p × E ^ m u l (17) E_{mul}=m\times n\times p\times\hat{E}_{mul}\tag{17} \\ Emul=m×n×p×E^mul(17)
对于BitNet,由于权重是1-bit,因此矩阵乘法的能量消耗是由加法运算决定的。乘法运行仅应用于因子 β \beta β和 γ Q b \frac{\gamma}{Q_b} Qbγ缩放输出,因此乘法的能量消耗可以计算为:
E m u l = ( m × p + m × n ) × E ^ m u l (18) E_{mul}=(m\times p+m\times n)\times\hat{E}_{mul}\tag{18} \\ Emul=(m×p+m×n)×E^mul(18)
其明显小于Transformer。
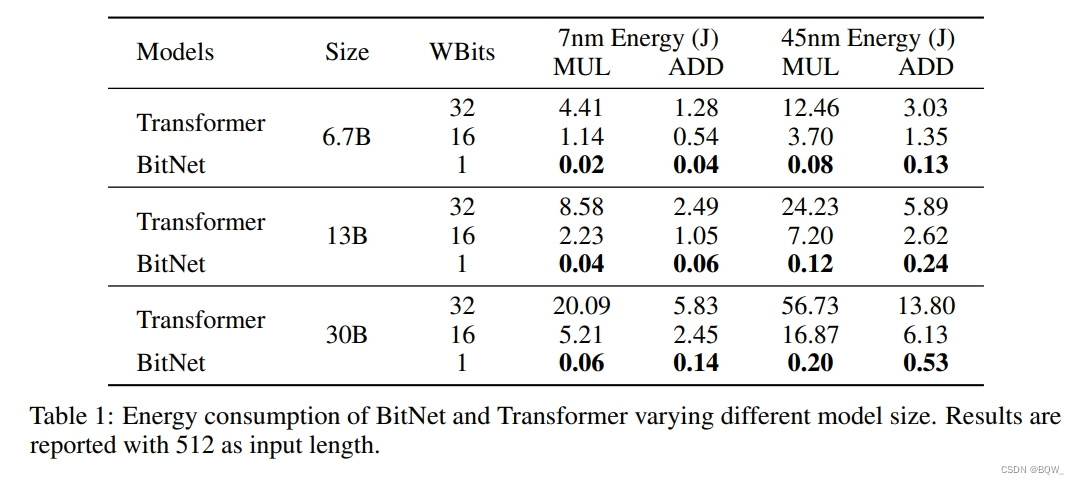
W1A8 BitNet相较于全精度(32-32)和半精度(16-16)的结果如上表1所示。可以看到,BitNet能够显著的节约能源。
三、与FP16 Transformer的比较
1. 设置
训练了一系列自回归BitNet模型,尺寸从125M至30B。这些模型是在英文语料上训练,包含Pile、Common Crawl 、RealNews和CC-Stories数据集。使用Sentencepiece tokenizer来预处理数据,词表尺寸为16K。除了BitNet,也用相同的数据集训练了Transformer baselines用于公平比较。
2. Inference-Optimal Scaling Law
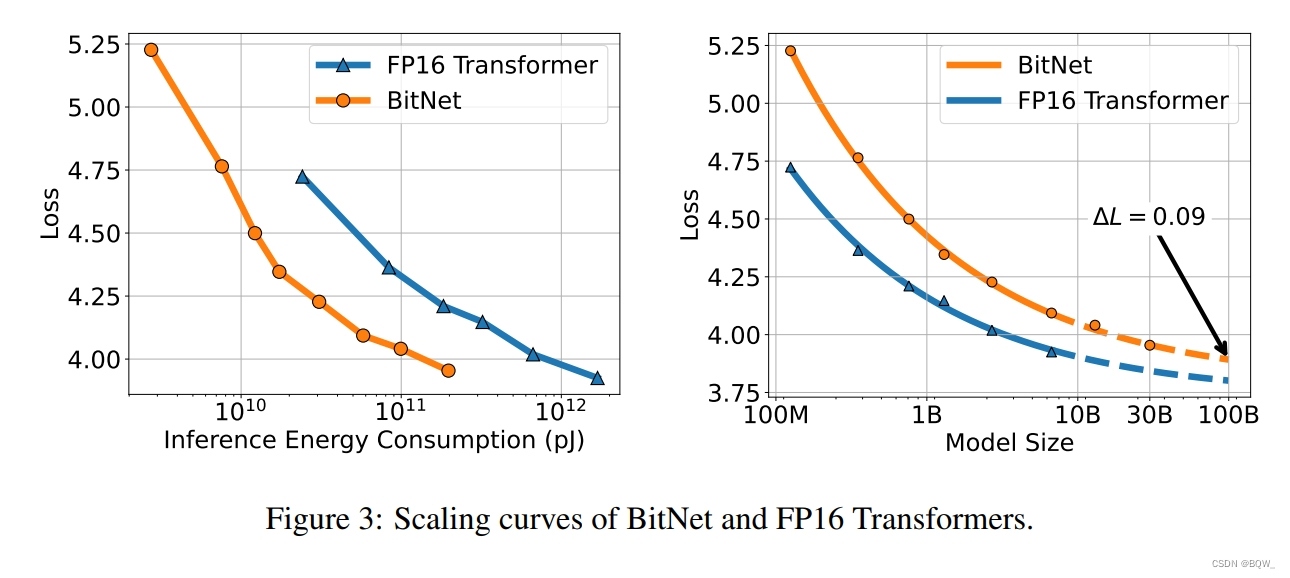
标准Transformer自然语言模型已经被证明可以预测缩放的结果,损失值的大小由训练所使用的计算量决定。这使得能够确定计算预算的最佳分配,并从较小的模型中预测大型语言模型的性能。
为了研究二值化Transformer的scaling law,绘制了BitNet和FP16 Transformer的scaling curve。上图3展示了BitNet的loss scaling,类似于FP16 Transformer,遵循幂律。这里用一个不可约损失项来拟合scaling law:
L ( N ) = a N b + c (19) L(N)=aN^b+c\tag{19} \\ L(N)=aNb+c(19)
为了评估scaling law是否能够准确预测loss,从125M至6.7B的模型来拟合幂律中的参数,并使用该定律来预测13B和30B的损失。结果表明,拟合后的scaling law能够准确的预测BitNet的损失函数。此外,随着模型尺寸的增加,BitNet和FP16 Transformer之间的差距越来越小。
上面的scaling law并没有正确地建模损失值和实际计算之间的关系。先前的工作通过计算FLOPs来估计计算量,但是其不适用于由整数计算主导的1-bit模型。此外,其主要是用于衡量训练的计算量,而不是推理。为了更好地理解神经语言模型的scaling效率,这里引入了Inference-Optimal Scaling Law。这主要是关注推理的成本,因此其会随着模型的使用而增加,但训练成本只有一次。上图3展示了7nm处理器相对于推理能力成本的scaling curve,其表明BitNet有更高的scaling效率。在给定固定计算预算的情况下,BitNet实现了更好的loss。此外,推理成本要小得多,可以获得与FP16模型相同的性能。
3. 下游任务结果
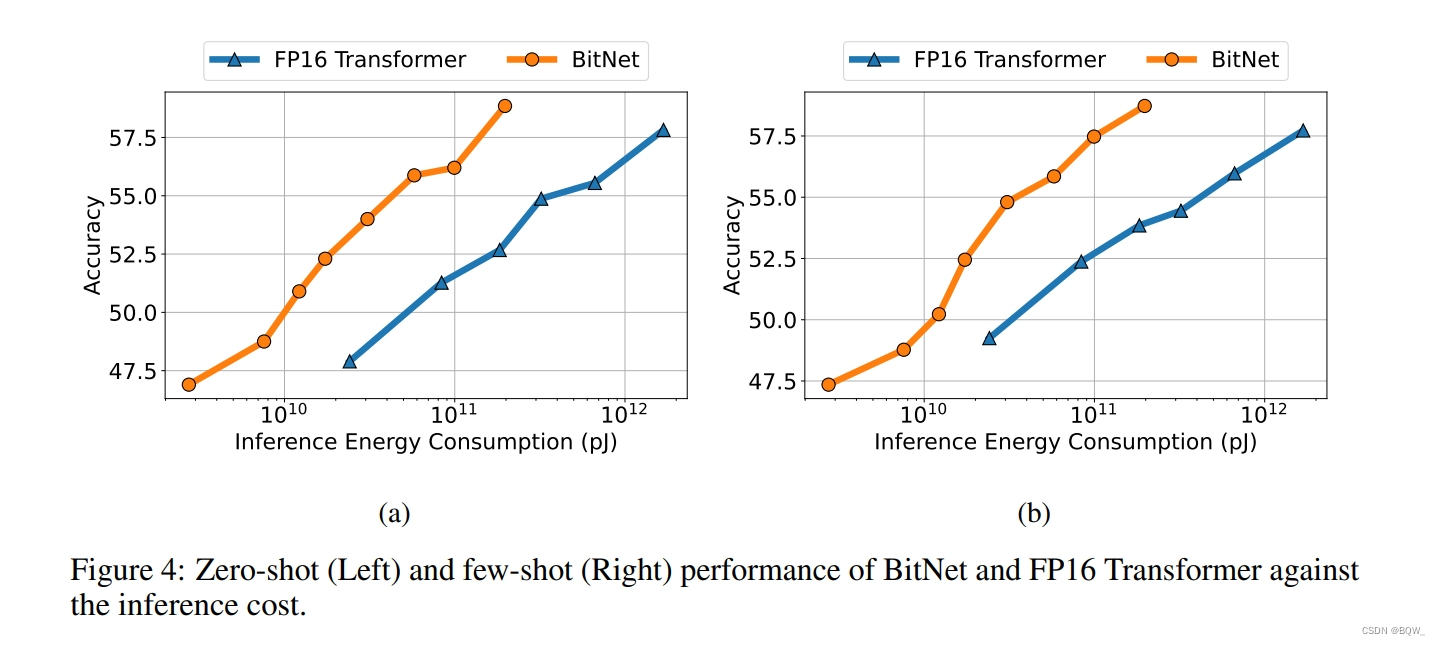
除了loss以外,还关注BitNet下游任务的能力。与loss相比,由于神经语言模型的涌现能力更难以预测。为了能够以可解释的度量来评估能力,在下游任务上测试了0-shot和4-shot的结果。上图4展示了不同规模的BitNet和FP16 Transformer的平均结果。与loss scaling curve类似,下游任务的性能可以随着计算预算的增加而增加。
4. 稳定性测试
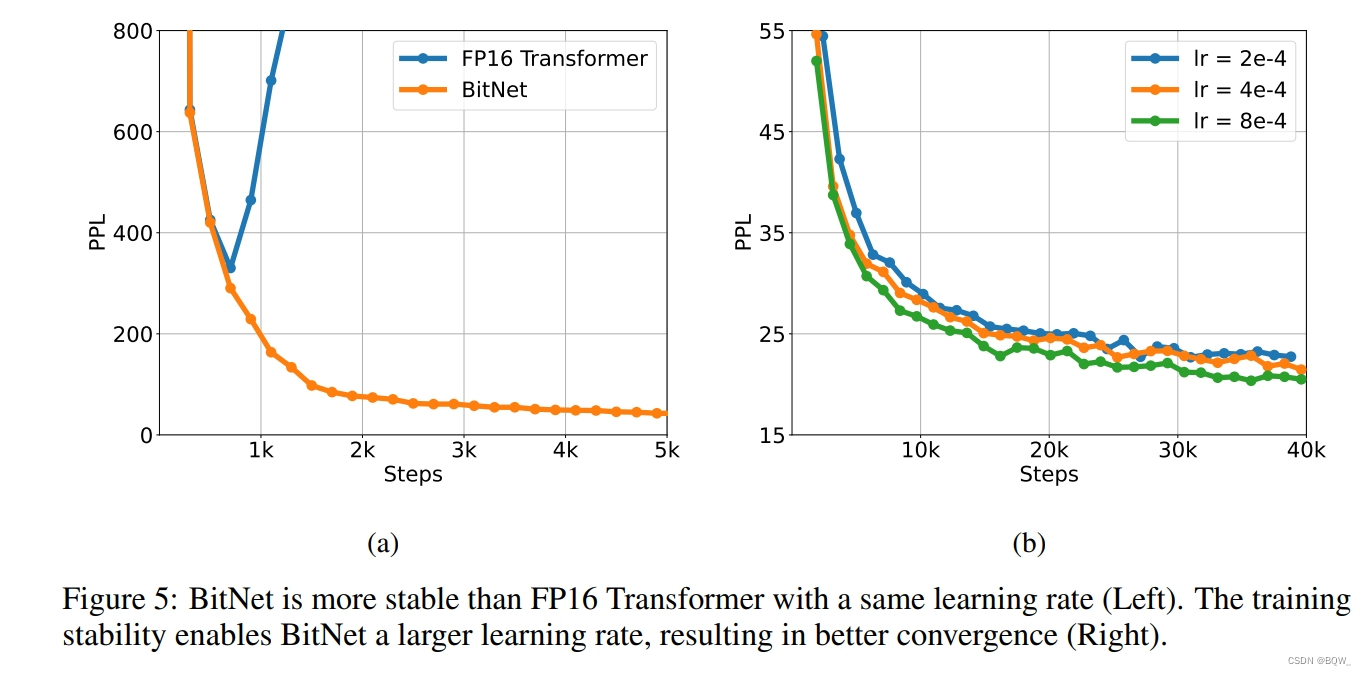
训练低精度Transformer的主要挑战是稳定性。因此,通过训练一系列具有不同峰值学习率的模型,对BitNet和FP16 Transformer进行了稳定性测试。上图5a展示了稳定性测试结果,表明BitNet可以以较大的学习率收敛,而FP16 Transformer则不能。上图5b展示了BitNet可以从增加的学习率中受益,实现PPL更好的收敛。
四、与Post-training量化的比较
1. 设置
这里将BitNet与最先进的量化方法进行了比较,包含Absmax、SmoothQuant、GPTQ和QulP。这些方法在FP16 Transformer模型上的post-training量化,其遵循与BitNet相同的训练设置和数据。其中,Absmax和SmoothQuant对权重和激活进行量化,而GPTQ和QulP只能降低权重的精度。应用这些方法在各种量化级别。对于weight-only量化,用W4A16和W2A16进行实验。对于权重和激活同时量化,将FP16 Transformer量化为W8A8、W4A4和W1A8。BitNet则使用二值权重和8-bit激活,其bits数小于等于baseline。
2. 结果
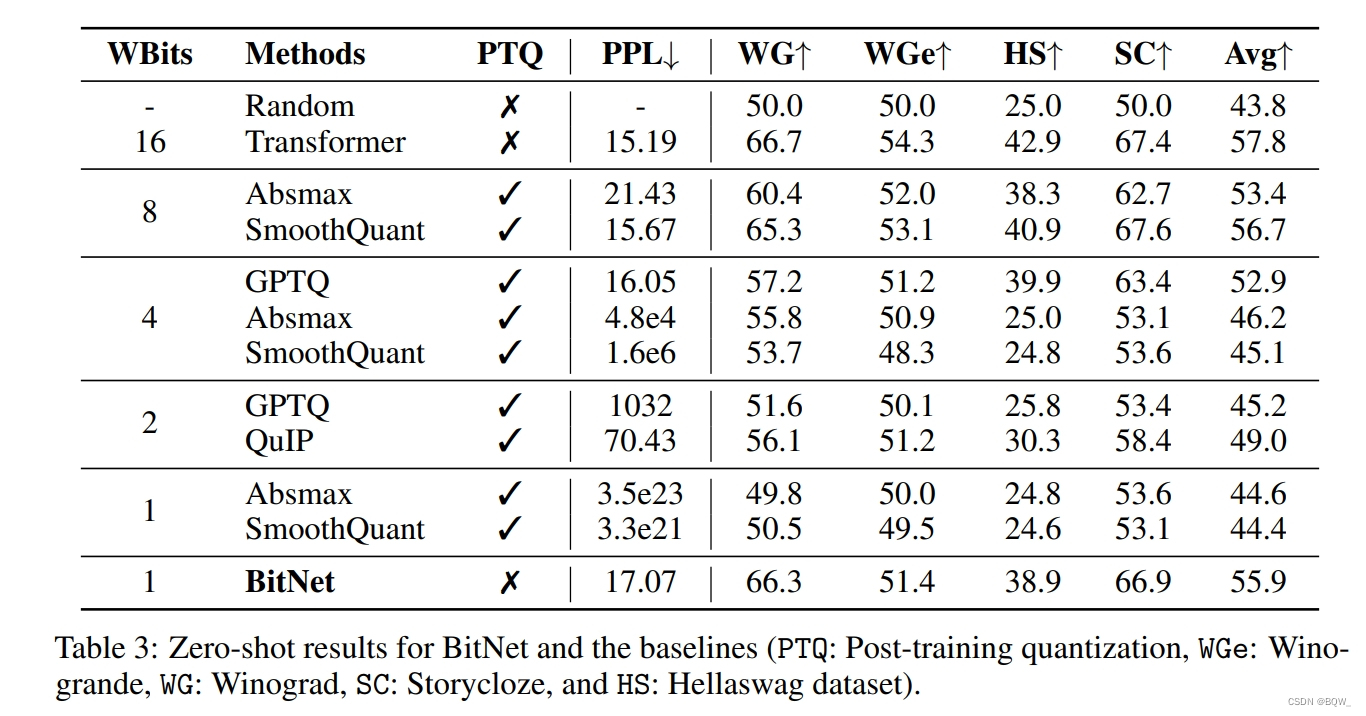
上面3是BitNet和各种baseline在四个基准数据集上zero-shot性能的详细分析。为了进行公平的比较,所有模型的大小均为6.7B。
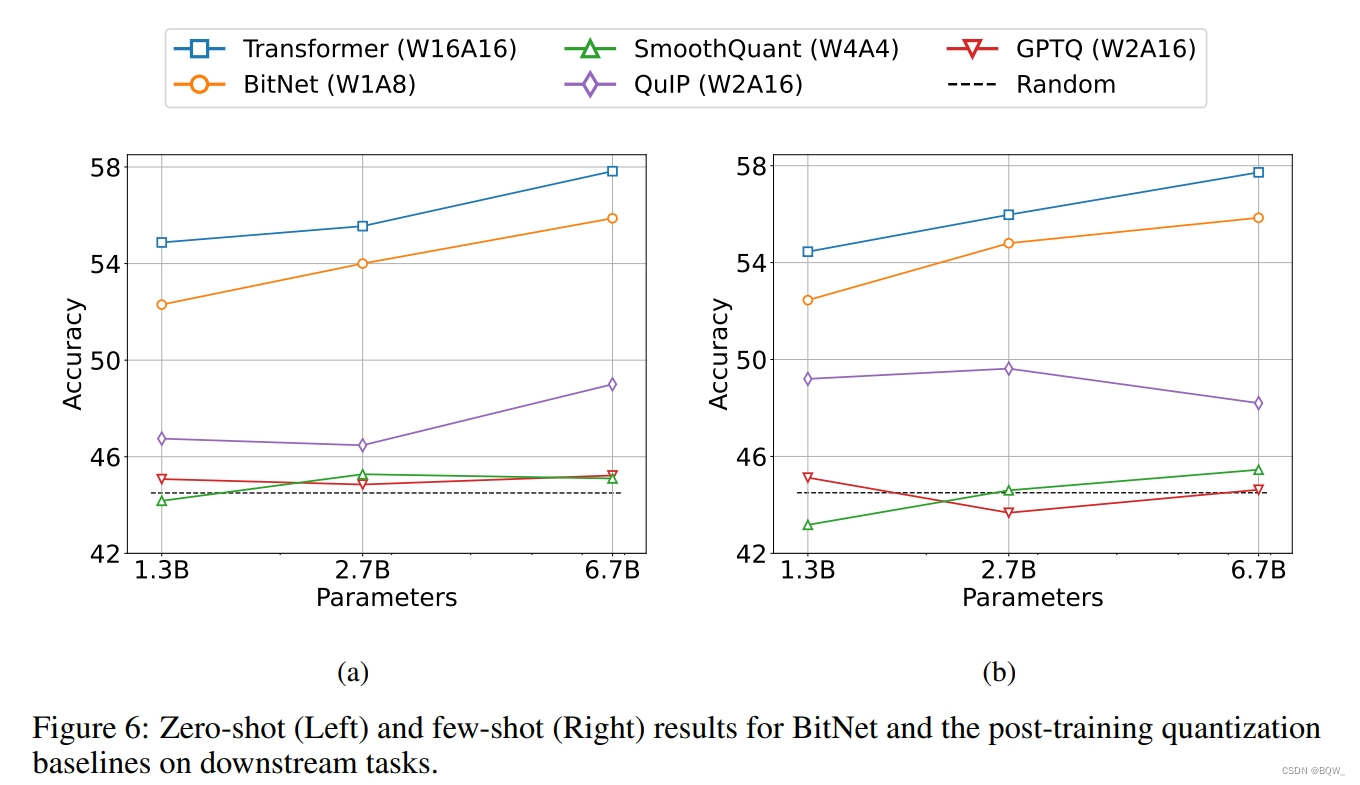
BitNet的zero-shot与8-bit模型相当,但是推理成本要低得多。对于4-bit模型,weight-only量化方法优于weight-and-activation量化方法,主要是因为激活更难量化。BitNet作为1-bit模型,显著优于各种量化方法。
相关文章:

【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM
BitNet:用1-bit Transformer训练LLM 《BitNet: Scaling 1-bit Transformers for Large Language Models》 论文地址:https://arxiv.org/pdf/2310.11453.pdf 相关博客 【自然语言处理】【大模型】BitNet:用1-bit Transformer训练LLM 【自然语言…...
安装及管理docker
文章目录 1.Docker介绍2.Docker安装3.免sudo设置4. 使用docker命令5.Images6.运行docker容器7. 管理docker容器8.创建image9.Push Image 1.Docker介绍 Docker 是一个简化在容器中管理应用程序进程的应用程序。容器让你在资源隔离的进程中运行你的应用程序。类似于虚拟机&#…...
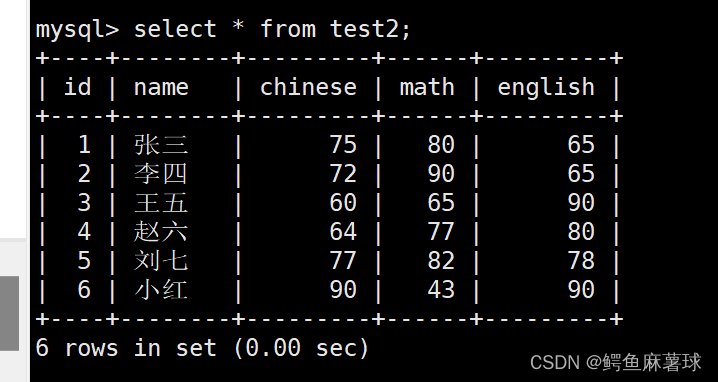
【MySQL】表的增删改查——MySQL基本查询、数据库表的创建、表的读取、表的更新、表的删除
文章目录 MySQL表的增删查改1. Create(创建)1.1 单行插入1.2 多行插入1.3 替换 2. Retrieve(读取)2.1 select查看2.2 where条件2.3 结果排序2.4 筛选分页结果 3. Update(更新)3.1 更新单个数据3.2 更新多个…...

C/C++蓝桥杯之日期问题
问题描述:小明正在整理一批文献,这些文献中出现了很多日期,小明知道这些日期都在1960年1月1日至2059年12月31日之间,令小明头疼的是,这些日期采用的格式非常不统一,有采用年/月/日的,有采用月/日…...

【理解指针(二)】
文章目录 一、指针的运算(1)指针加整数(2)指针减指针(指针关系运算) 二、野指针(1)野指针的成因(1.1)指针未初始化(1.2)指针的越界访问…...

使用AI纠正文章
我写了一段关于哲学自学的读书笔记,处于好奇的目的,让AI帮我纠正语法和逻辑。我的原文如下: 泰勒斯第一次提出了水是万物本源的说法,对于泰勒斯为什么提出这样的观点,或者是这样的观点是怎么来的,我们无从所…...

拼多多API批量获取商品详情信息
随着电子商务的蓬勃发展,淘宝作为中国最大的在线购物平台之一,每天需要处理海量的商品上架和交易。为了提高工作效率,自动化上架商品和批量获取商品详情信息成为了许多商家和开发者的迫切需求。本文将详细介绍淘宝的API接口及其相关技术&…...
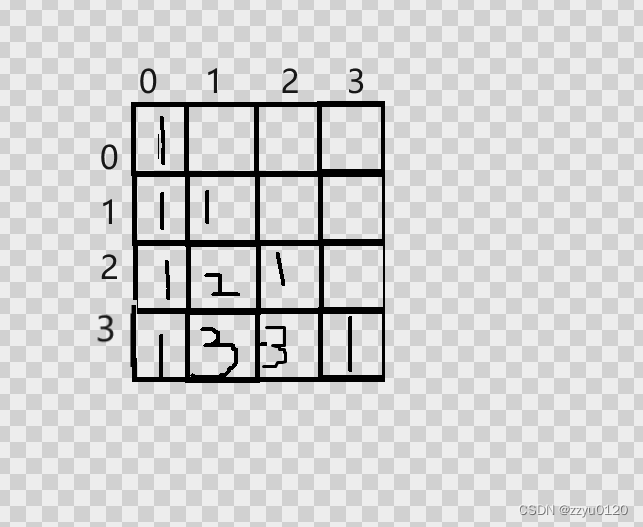
杨辉三角(C语言)
杨辉三角 一.什么是杨辉三角 一.什么是杨辉三角 每个数等于它上方两数之和。 每行数字左右对称,由1开始逐渐变大。 第n行的数字有n项。 前n行共[(1n)n]/2 个数。 … 当前行的数上一行的数上一行的前一列的数 void yanghuisanjian(int arr[][20], int n) {for (int i…...

宏任务与微任务:JavaScript异步编程的秘密
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...
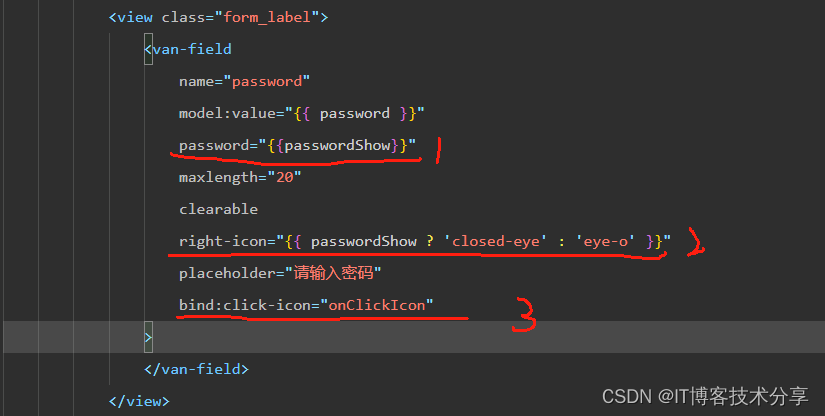
vant van-field 密码输入框小程序里隐藏、显示密码bug总结
老规矩先上效果图: vant 输入框组件 密码的隐藏与显示功能: 注: 用password属性控制密码的显示与隐藏 不要用type属性,type属性在真机上有时会没有效果 1、当然如果只用typepassword 不需要切换显示、隐藏也可以使用。 2、如果用到了密码的显示与…...

代理ip应用场景
代理IP是一种网络技术,它允许用户通过中间来访问互联网资源,隐藏真实的IP地址代理IP的应用场景非常泛,以下是一些常见的应用场景: 1 隐私保护:使用代理IP可以隐藏用户的真实IP地址,保护个人隐私。在浏览网…...

C/C++指针详解
接下来我们来介绍一下什么是指针? 指针其实就是元素存放地址,更加形象的比喻:在酒店中如果你想要去注必须去付费不然不能住,在计算机也同样如此(但是不需要付费哦)每当我们使用一个变量或其他需要申请空间…...

实验一:华为VRP系统的基本操作
1.1实验介绍 1.1.1关于本实验 本实验通过配置华为设备,了解并熟悉华为VRP系统的基本操作 1.1.2实验目的 理解命令行视图的含义以及进入离开命令行视图的方法 掌握一些常见的命令 掌握命令行在线帮助的方法 掌握如何撤销命令 掌握如何使用命令快捷键 1.1.3实验组网 …...
ChatGPT发不出消息?GPT发不出消息怎么办?
前言 今天发现,很多人的ChatGPT无法发送信息,我就登陆看一下自己的GPT的情况,结果还真的无法发送消息,ChatGPT 无法发送消息,但是能查看历史的对话,不过通过下面的方法解决了。 第一时间先打开官方的网站&a…...

【论文笔记】Language Models are Few-Shot Learners
Language Models are Few-Shot Learners 回顾一下第一代 GPT-1 : 设计思路是 “海量无标记文本进行无监督预训练少量有标签文本有监督微调” 范式;模型架构是基于 Transformer 的叠加解码器(掩码自注意力机制、残差、Layernorm)&a…...

解决:Glide 在回调中再次加载图片报错
一、问题说明 Glide 加载图片时监听了回调,并在失败时再次加载其它图片后报错。 代码: Glide.with(mContext).load(imgTeacher).listener(new RequestListener<Drawable>() {Overridepublic boolean onLoadFailed(Nullable GlideException e, O…...

Java学习笔记之IDEA的安装与下载以及相关配置
1 IDEA概述 IDEA全称IntelliJ IDEA,是用于Java语言开发的集成环境,它是业界公认的目前用于Java程序开发最好的工具。 集成环境: 把代码编写,编译,执行,调试等多种功能综合到一起的开发工具。 2 IDEA…...
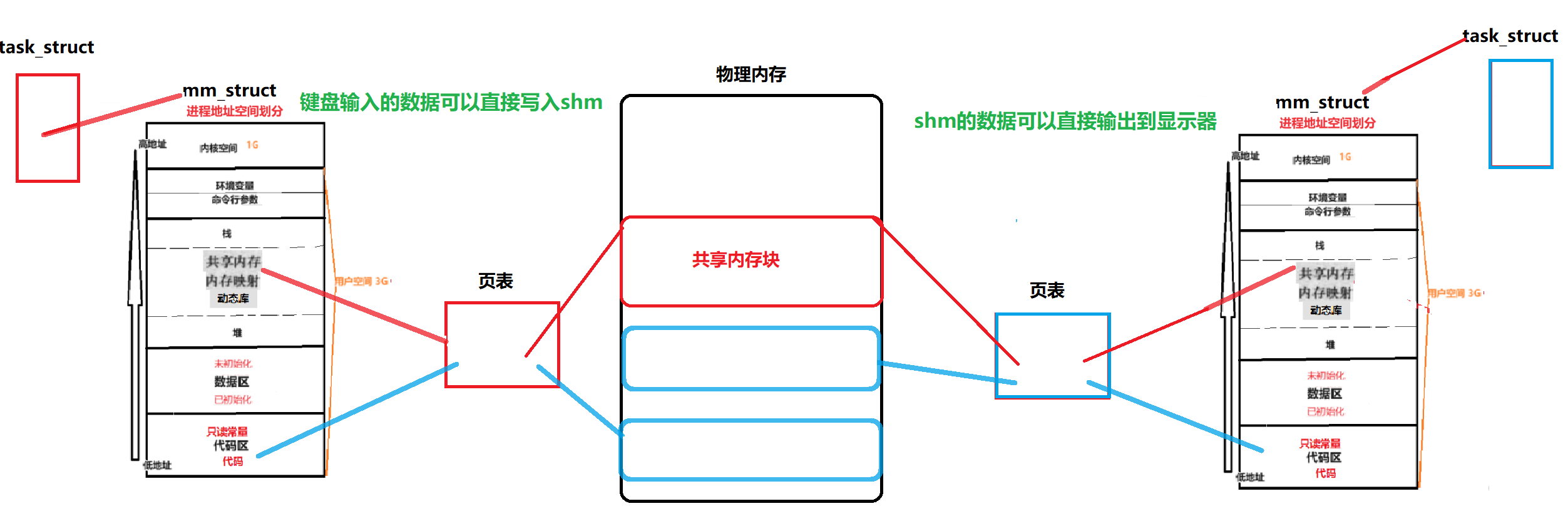
【共享内存】System V共享内存{通信原理/相关接口/代码测试}
文章目录 1.初识共享内存1.0浅谈System V1.1什么是共享内存?1.2Linux-System V共享内存1.3图解共享内存1.4对共享内存的理解 2.创建共享内存2.1共享内存如何创建?2.2代码运行与测试2.3shm与pipe的区别2.4shm缺乏访问控制 3.代码理解shm3.1Log.hpp3.2comm…...
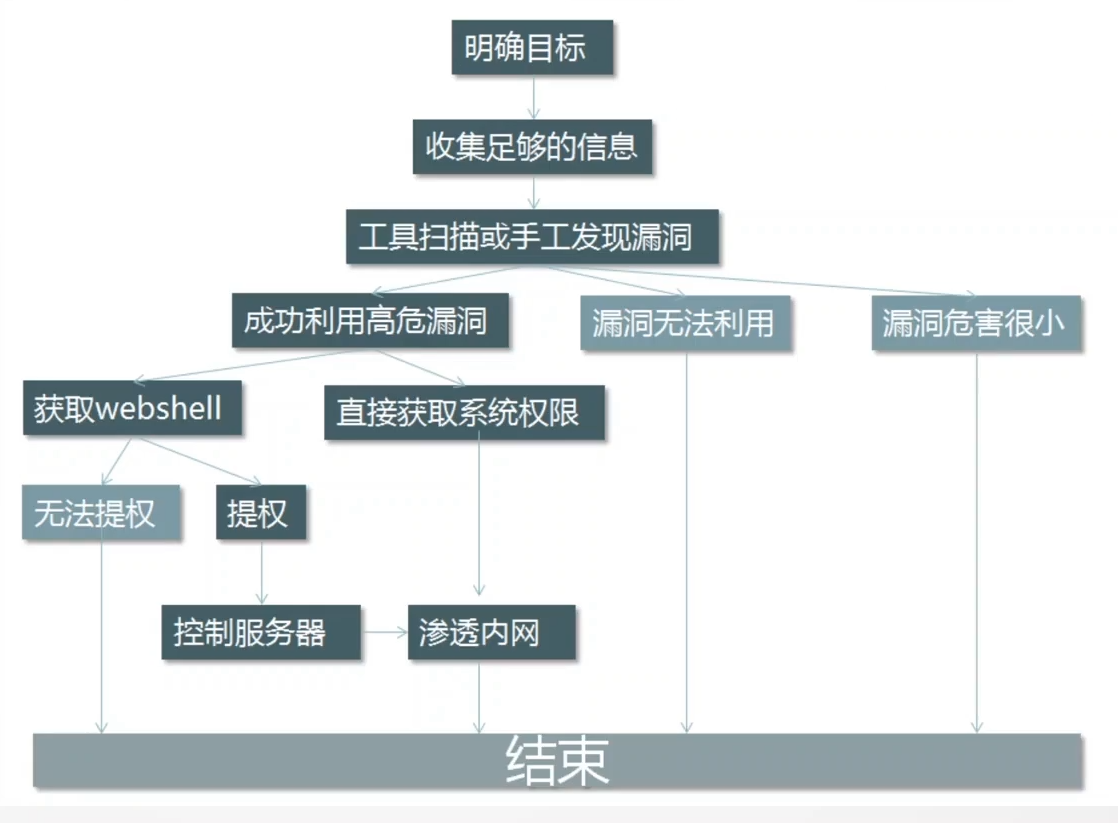
Web渗透测试流程
什么是渗透测试 渗透测试 (penetration test),是通过模拟恶意黑客的攻击方法,来评估计算机网络系统安全的一种评估方法。这个过程包括对系统的任何弱点、技术缺陷或漏洞的主动分析,这个分析是从一个攻击者可能存在的位置来进行的,并且从这个…...

探索机器学习的无限可能性:从初学者到专家的旅程
探索机器学习的无限可能性:从初学者到专家的旅程 在当今数字时代,机器学习无疑是最引人注目的技术之一。它已经深入到我们生活的方方面面,从个性化推荐到自动驾驶汽车,再到医疗诊断和金融预测。但是,即使我们已经见证…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
