蓝桥杯刷题5--GCD和LCM
目录
1. GCD
1.1 性质
1.2 代码实现
2. LCM
2.1 代码实现
3. 习题
3.1 等差数列
3.2 Hankson的趣味题
3.3 最大比例
3.4 GCD
1. GCD
整数a和b的最大公约数是能同时整除a和b的最大整数,记为gcd(a, b)
1.1 性质
GCD有关的题目一般会考核GCD的性质。
(1)gcd(a, b) = gcd(a, a+b) = gcd(a, k·a+b)
(2)gcd(ka, kb) = k·gcd(a, b)
(3)多个整数的最大公约数:gcd(a, b, c) = gcd(gcd(a, b), c)
(4)若gcd(a, b) = d,则gcd(a/d, b/d) = 1,即a/d与b/d互素
(5)gcd(a+cb, b) = gcd(a, b)
1.2 代码实现
import java.math.BigInteger;
public class Main {public static void main(String[] args) {System.out.println(gcd(45, 9)); // 9System.out.println(gcd(0, 42)); // 42System.out.println(gcd(42, 0)); // 42System.out.println(gcd(0, 0)); // 0System.out.println(gcd(20, 15)); // 5System.out.println(gcd(-20, 15)); // -5System.out.println(gcd(20, -15)); // 5System.out.println(gcd(-20, -15)); // -5System.out.println(gcd(new BigInteger("98938441343232"), new BigInteger("33422"))); // 2}public static long gcd(long a, long b) {if (b == 0) return a; return gcd(b, a % b);}public static BigInteger gcd(BigInteger a, BigInteger b) {return a.gcd(b);}
}
2. LCM
最小公倍数LCM(the Least Common Multiple)。a和b的最小公倍数lcm(a, b),从算术基本定理推理得到。
2.1 代码实现
public static int gcd(int a, int b) {if (b == 0) return a; return gcd(b, a % b);}public static long lcm(int a, int b) {return (long) a / gcd(a, b) * b;}
3. 习题
3.1 等差数列

import java.util.*;
public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int num = scan.nextInt();int arr[] = new int[num];for(int i = 0;i<num;i++){arr[i] = scan.nextInt();}Arrays.sort(arr);int min = 0;for(int i = 1;i<num;i++){min = gcd(min,arr[i] - arr[i-1]);}if(min == 0) System.out.println(num);else System.out.println((arr[num-1] - arr[0])/min+1);scan.close();}public static int gcd(int a ,int b){if(b==0) return a;return gcd(b,a%b);}
}这是gcd问题。把n个数据排序,计算它们的间隔,对所有间隔做GCD,结果为公差。最少数量等于:(最大值-最小值)/公差+1
3.2 Hankson的趣味题

import java.util.*;
public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();for(int i = 0;i<n;i++){int a0 = scan.nextInt();int a1 = scan.nextInt();int b0 = scan.nextInt();int b1 = scan.nextInt();int count = 0;for(int x = 1;x<=Math.sqrt(b1);x++){if(b1%x == 0){if(gcd(x,a0) == a1 && lcm(x,b0) == b1){count++;} int y = b1 / x;if (x == y){continue; } if (gcd(y, a0) == a1 && lcm(y, b0) == b1){count++; }}}System.out.println(count);}scan.close();}public static int gcd(int a,int b){if(b==0) return a;return gcd(b,a%b);}public static int lcm(int a,int b){return a/gcd(a,b)*b;}
}3.3 最大比例

import java.util.*;
public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int num = scan.nextInt();long arr[] = new long[num];for(int i = 0;i<num;i++){arr[i] = scan.nextLong();}Arrays.sort(arr);long q = Long.MAX_VALUE;long t0 = 0;long t1 = 0;for(int i = 0;i<num-1;i++){if(arr[i+1]!=arr[i] && arr[i+1]/arr[i] < q){q = arr[i+1]/arr[i];t0 = arr[i];t1 = arr[i+1];}}long k = gcd(t0,t1);System.out.println(t1/k + "/" + t0/k);scan.close();}public static long gcd(long a,long b){if(b==0) return a;return gcd(b,a%b);}
}3.4 GCD

import java.util.*;
public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);long a = scan.nextLong();long b = scan.nextLong();long c = Math.abs(a-b);System.out.println(c - a%c);scan.close();}
}根据更相减损术可以知道一个等式:gcd(a,b)=gcd(a,b-a) 当然这里的前提是a<=b; 所以gcd(a+k,b+k)=gcd(a+k,b-a) 这里的a和b都是已知的 我们可以设c=b-a 即c是已知的 所以想要使得a+k与c的最大公因子尽可能地大 因为最大最大能到达c 显然这个式子的最大gcd一定为 c ,我们只需要计算出a 最少需要增加多少可以成为 c 的倍数,这个增量即是答案k
相关文章:

蓝桥杯刷题5--GCD和LCM
目录 1. GCD 1.1 性质 1.2 代码实现 2. LCM 2.1 代码实现 3. 习题 3.1 等差数列 3.2 Hankson的趣味题 3.3 最大比例 3.4 GCD 1. GCD 整数a和b的最大公约数是能同时整除a和b的最大整数,记为gcd(a, b) 1.1 性质 GCD有关的题目一般会考核GCD的性质。 …...

LVS+Keepalived 高可用负载均衡集群
一. 高可用集群的相关知识 1.1 高可用(HA)集群和普通集群的比较 ① 普通集群 普通的群集的部署是通过一台度器控制调配多台节点服务器进行业务请求的处理,但是仅仅是一台调度器,就会存在极大的单点故障风险,当该调度…...
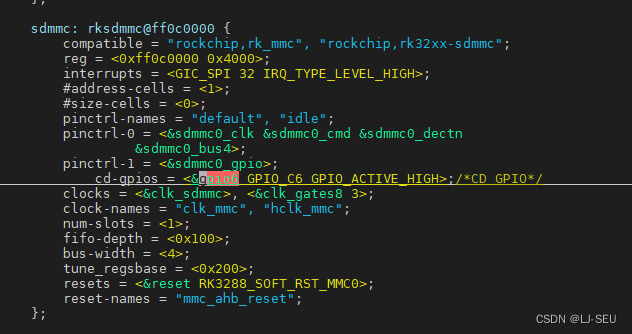
【RK3288 Android6, T8PRO 快捷按键 gpio 配置上拉输入】
文章目录 【RK3288 Android6, T8PRO 快捷按键 gpio 配置上拉输入】需求开发过程尝试找到没有用的上拉gpio尝试修改pwm1的gpio的默认上拉模式 改动 【RK3288 Android6, T8PRO 快捷按键 gpio 配置上拉输入】 需求 T8pro想要模仿T10 的 快捷按键ÿ…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:LoadingProgress)
用于显示加载动效的组件。 说明: 该组件从API Version 8开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 无 接口 LoadingProgress() 创建加载进展组件。 从API version 9开始,该接口支持在ArkTS卡片中使…...

隐私与创新的交汇点:Partisia Blockchain 重绘技术蓝图
正当我们在这个信息泛滥的时代寻找稳固的信任锚点时,区块链技术应运而生,然而,正如任何科技革命都会遇到的挑战,一个重要的问题摆在了我们面前:如何在不牺牲个人隐私的前提下,享受区块链技术带来的好处&…...

小程序 van-field label和输入框改成上下布局
在组件上面加个样式就行:custom-style"display:block;" <van-field label"备注说明" type"textarea" clearable title-width"100px" custom-style"display:block;" placeholder"请输入" /> …...
)
跨域资源共享(CORS)
预检请求 预检请求(Preflight Request)是跨域资源共享(CORS)机制中的一种特殊请求,主要用于在实际请求之前进行安全性检查。当一个请求可能不满足同源策略(即请求的源与目标资源的源不同,源包括…...
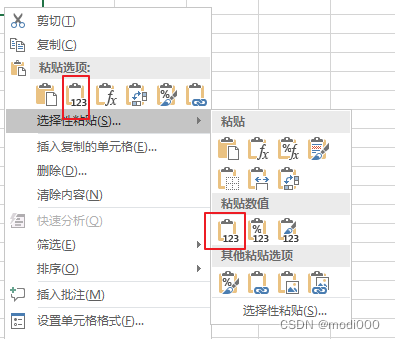
excel中去除公式,仅保留值
1.单个单元格去除公式 双击单元格,按F9. 2.批量去除公式 选中列然后复制,选择性粘贴,选值粘贴...

大数据和数据要素有什么关系?
大数据与数据要素之间存在密切的关系。大数据是指海量、多样化、高速生成的数据,而数据要素是指构成数据的基本元素或属性。数据要素包括但不限于数据的类型、结构、格式、单位、精度等。 大数据的产生和应用离不开数据要素的支持。数据要素确定了数据的基本特征和…...
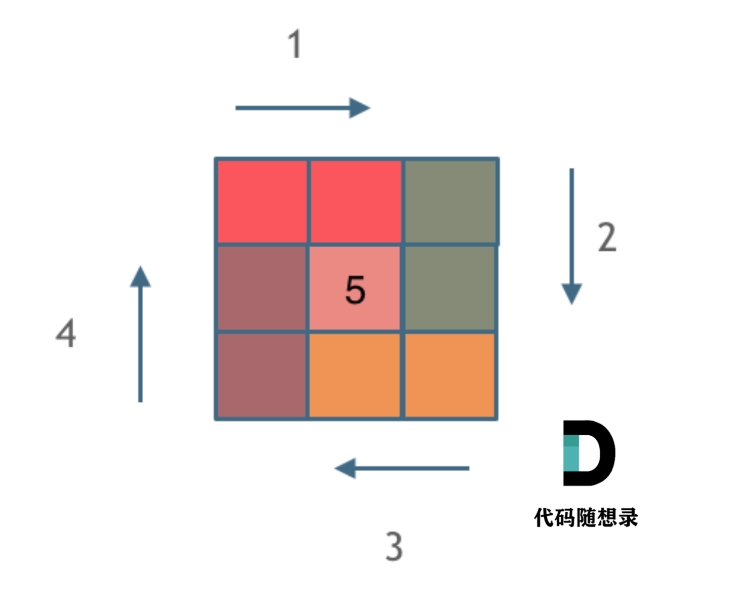
Leetcode 59.螺旋矩阵Ⅱ
1.题目 2.思路 (借用代码随想录的图) 1.我们将转一圈看作一个循环(1->2->3->4->5->6->7->8 这是一个循环) 2.在这个循环里,我们要画四条边(上右下左) 填充上行从左到右 填…...
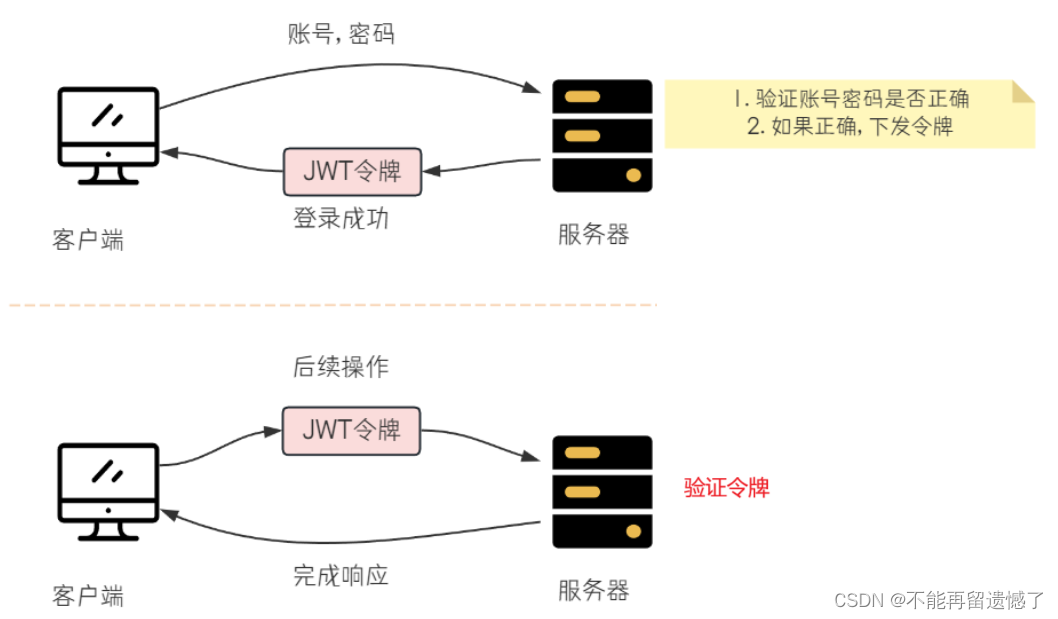
JWT令牌技术
文章目录 什么是令牌技术为什么需要令牌技术呢JWT 令牌JWT 组成JWT 令牌的使用1. 引入 JWT 依赖生成 JWT 令牌解析 JWT 令牌 什么是令牌技术 令牌技术是一种重要的安全技术,它在多个领域中发挥着关键作用。简单来说,令牌(Token)可…...

从零学习Linux操作系统 第三十二部分 ansible中剧本的应用
一、什么是playbook及playbook的组成 1.Playbook的功能 playbook 是由一个或多个play组成的列表 Playboot 文件使用YAML来写的 play就是一个个模块用列表的方式体现出来 playbook的语法是用YAML的预防进行书写的 2.YAML 简介 是一种表达资料序列的格式,类似XM…...
目标网站屏蔽右键检查(使用开发者工具)
问题: 通过网络触手中想要获取某网站的数据出现:鼠标右击,或按ctrl F10 键 无反应(也就是打不开类似谷歌的开发工具) 问题同等与: 解决网页屏蔽F12或右键打开审查元素 引用: 作者ÿ…...
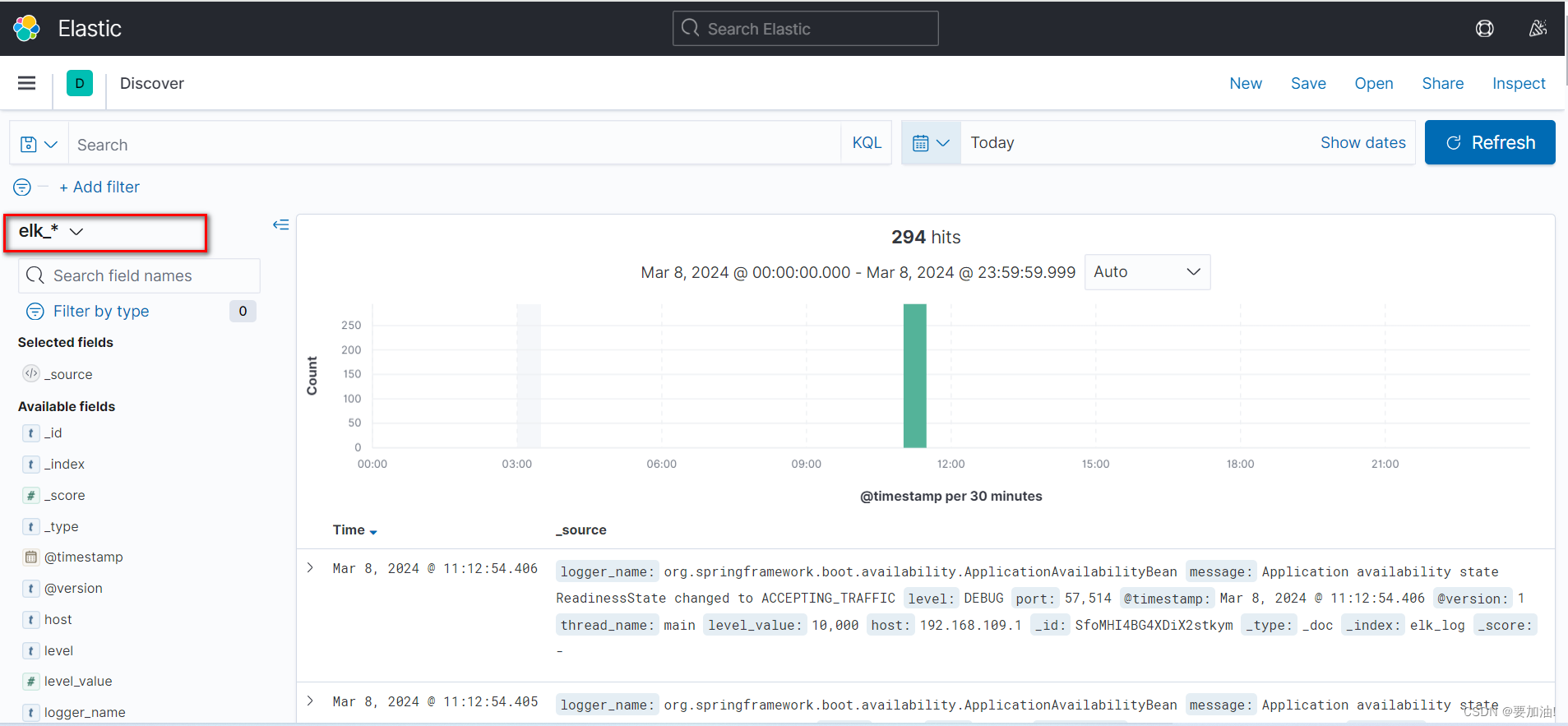
docker安装ES、LogStash、Kibana
文章目录 一、安装Elasticsearch1. 安装Elasticsearch2. 安装IK分词器3. elasticsearch-head 监控的插件4. 配置跨域 二、安装LogStash三、安装kibana四、SpringBoot集成LogStash,将日志输出到ES中五、 启动项目,监控项目运行 提示:以下是本篇…...

解决对接淘宝开放平台添加商品图片问题
问题 之前工作因队友离开,只一天接手其部分且第二天就要上线此工具产品,测试提了一些Bug,在Bug中有一个是添加商品图片。前端告知不能用、电话离职队友说能用。没办法自己上、追踪代码。 en这块代码跟需求好像不太相符,重写。 …...
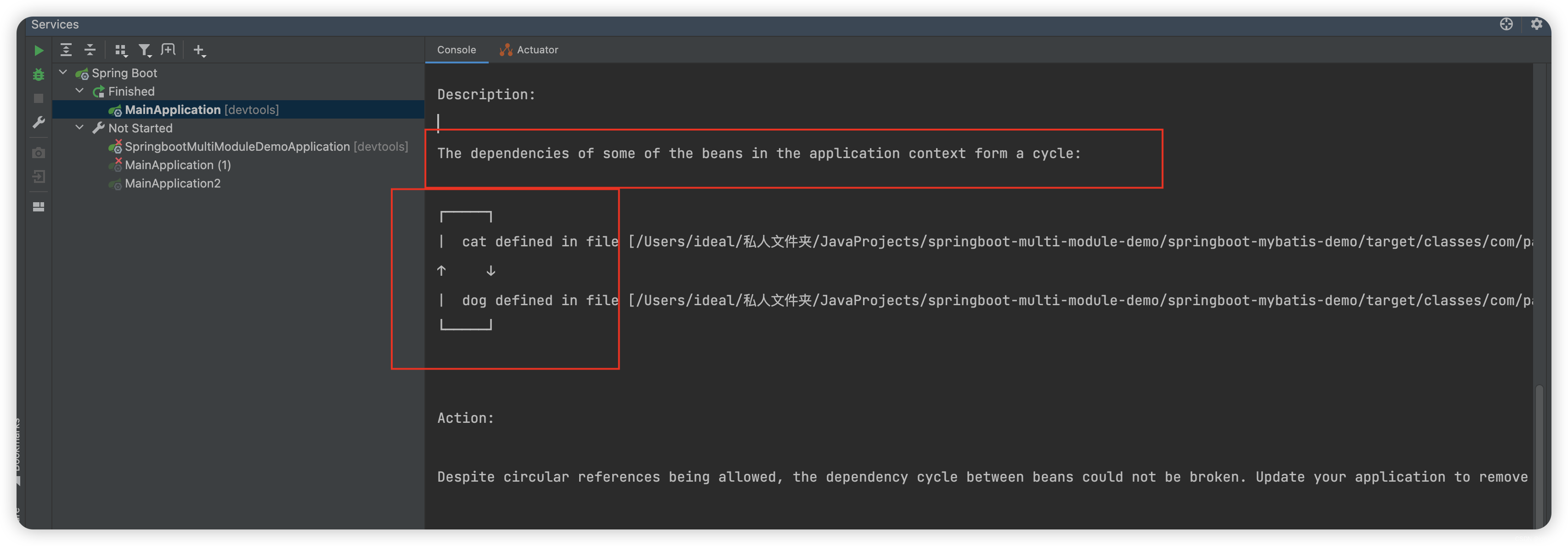
总结:Spring创建Bean循环依赖问题与@Lazy注解使用详解
总结:Spring创建Bean循环依赖问题与Lazy注解使用详解 一前提知识储备:1.Spring Bean生命周期机制(IOC)2.Spring依赖注入机制(DI)(1)Autowired注解标注属性set方法注入(2&…...

Mac下java环境搭建
JDK 教程:MAC安装JDK及环境变量配置-CSDN博客 建议JDK7和JDK8都装上,因为一些老项目是用JDK7开发,使用JDK8编译时报错。(若没有老项目,直接安装jdk8) 若配置环境变量时找不到JDK的安装路径,有两种方式: 方式一、mac默认位置为:/Library/Java/JavaVirtualMachines/…...

mac设置java环境变量
在 macOS 系统上,设置 JAVA_HOME 环境变量可以通过以下步骤进行: 打开终端应用程序。 输入以下命令来查找 Java 的安装路径:/usr/libexec/java_home 终端会返回 Java 的安装路径,类似 /Library/Java/JavaVirtualMachines/jdk1.…...

【笔记】Android 漫游定制SPN定制有关字段
一、SPN模块简介 【笔记】SPN和PLMN 运营商网络名称显示 Android U 配置 WiFiCalling 场景下PLMN/SPN 显示的代码逻辑介绍 【笔记】Android Telephony 漫游SPN显示定制(Roaming Alpha Tag) 二、相关配置字段 non_roaming_operator_string_array 是否…...
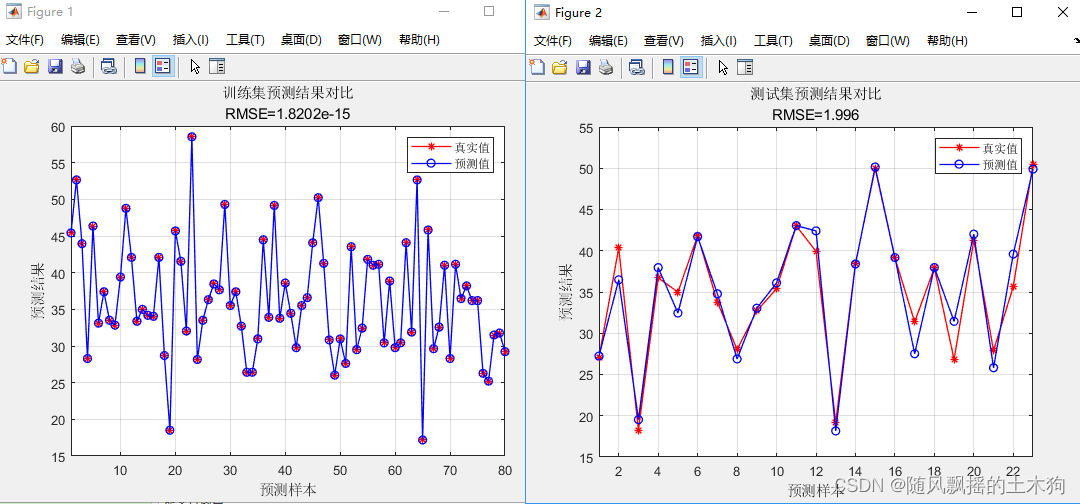
【MATLAB第99期】#源码分享 | 基于MATLAB的SHEPard模型多输入单输出回归预测模型
【MATLAB第99期】#源码分享 | 基于MATLAB的SHEPard模型多输入单输出回归预测模型 Shepard模型(简称SP模型)就是一种直观的、可操作的相似预测法,常用于插值。相似预测法基本原理按照相似原因产生相似结果的原则,从历史样本中集中找出与现在的最相似的一…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
