代码随想录刷题笔记 DAY 42 | 最后一块石头的重量 II No.1049 | 目标和 No.494 | 一和零 No.474
文章目录
- Day 43
- 01. 最后一块石头的重量 II(No. 1049)
- <1> 题目
- <2> 笔记
- <3> 代码
- 02. 目标和(No. 494)
- <1> 题目
- <2> 笔记
- <3> 代码
- 03. 一和零(No. 474)
- <1> 题目
- <2> 笔记
- <3> 代码
Day 43
01. 最后一块石头的重量 II(No. 1049)
题目链接
代码随想录题解
<1> 题目
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40]
输出:5
提示:
1 <= stones.length <= 301 <= stones[i] <= 100
<2> 笔记
这道题其实和上一篇的 分割等和子集(No. 416) 非常类似,难点都是如何想出递归的思路。
在前面也提到过,动态规划其实就是用来求最值的,当看到可以利用最值求解的时候,就可以考虑递归的思路。
既然要求出什么时候两块石头能够相互抵消的最多,其实可以转换成 如何将这一堆石头分成两堆质量和 最 相近的石头;如果要分成最相近的两堆石头,那这个临界点就是这两堆石头重量 相等 的时候,即完全抵消的时候,也就是 约束 两堆重量最大值的条件有一条是:最大重量不能超过 sum / 2 也就是总重量的二分之一。
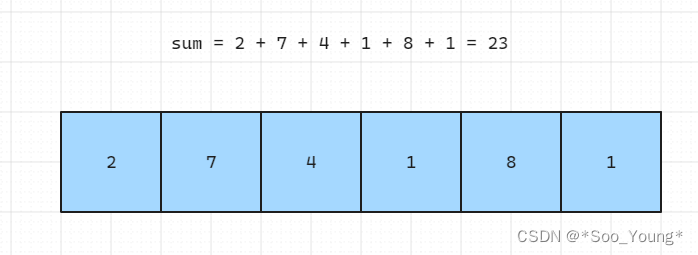
这时候得到了一堆中的最大重量,假设是 m 另一堆的最大重量也就是 sum - m,最终剩余的 重量 也就是
sum - 2 * m。
💡 说到这里其实很多人会思考如果
sum是奇数的话,应该是向下取整还是向上取整呢?
- 其实是都可以的,比如上面那个例子当一堆中的物品取到可以将最大重量设定为
12也可以设定为11- 站在总体的角度看,一堆中的重量想着
11或者12靠近的时候,剩余的那一堆也是向它的目标靠近的- 最终取得结果的时候就是整体的最优情况
但是如果求最大的那部分那最终的结果其实不好处理,因为这时候是依赖于 理论上的最大值 来进行限制的,只能说 其中一个部分 一定不会超过 这个理论上的最大值,但是另一部分却不一定,比如上题中的示例 2 ,它的两堆分别是 73 和 78,如果我们向上取整的话,其实最后还是要分辨 最终求得的部分是大的那一堆还是小的那一堆的,比如示例 1 的情况。
但如果向下取整就不会出现这种情况,因为这部分一定是小的那一堆;所以两种方式其实都可以,但是向下取整对结果的处理更加简单。
有一个限制(target)是 sum / 2,又有一堆东西可以去选择,这不正是一个背包问题嘛?
当遇到背包问题的时候不要去和背包问题类比,这样很容易把自己搞混乱,而是要像一开始接触到背包问题那样从头开始推导:限制值为 target , dp[i][j] 是在当 前容量的限制下能够取得的最重的重量,对于一个石头可以选择 取或者不取,如果不取的话最终的重量其实就是 dp[i - 1][j] 如果取的话,最终得到的就是
dp[i - 1][j - stones[i]] + stones[j],这样能得到和 01 背包 一样的递推公式。
之所以说不要尝试去类比,是因为其实很多 物品 是不具备 value 属性的,强行去类比反而会比较混乱,重要的是利用背包问题的思想去推导。
写出代码,本题的代码和背包问题几乎完全相同。
<3> 代码
二维数组的方法
class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0; // 原本石头的总重量for (int i = 0; i < stones.length; i++) {sum += stones[i];}int[][] dp = new int[stones.length][sum/2 + 1];// 初始化 dp 数组for (int i = stones[0]; i < dp[0].length; i++) {dp[0][i] = stones[0];}for (int i = 1; i < stones.length; i++) {for (int j = 1; j < dp[0].length; j++) {if (j >= stones[i]) dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);else dp[i][j] = dp[i - 1][j];}}return sum - 2 * dp[stones.length - 1][sum / 2];}
}
滚动数组优化
class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0; // 原本石头的总重量for (int i = 0; i < stones.length; i++) {sum += stones[i];}int target = sum / 2;int[] dp = new int[target + 1];// 初始化 dp 数组for (int i = stones[0]; i < dp.length; i++) {dp[i] = stones[0];}for (int i = 1; i < stones.length; i++) {for (int j = target; j >= stones[i]; j--) {dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}
02. 目标和(No. 494)
题目链接
代码随想录题解
<1> 题目
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
<2> 笔记
本题较容易想出来的肯定是回溯算法,即每个元素有两种情况,加上这个元素或者减去这个元素,但回溯算法的时间复杂度是指数级别的,可能不是最佳的解法;我会在代码区域贴上我的回溯算法示例。
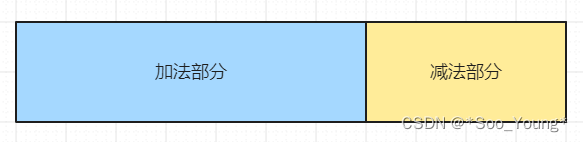
其实本题和上一题的思路比较类似,就是将这个集合去分成两部分,一部分是加法部分,另一部分是减法部分,只要将这两个部分相加得到的值是目标值即可。
这里设加法部分的总和为 m 减法部分的总和为 n,则可以得出 m - n = target,而又直到
m + n = sum,则可以有 m - (sum - m) = target 最终可以推导出 m = (target + sum) / 2 所以本题又变成了,从数组中选取元素,元素的总和能达到 (target + sum) / 2 的方式有多少种。
通过这个方程其实可以推出本题的一些判断条件
- 如果计算出来的
m是分数的话,那可以直接返回0,因为题目中给出的全是整数,不可能出现分数的情况 - 如果计算出来的
sum的绝对值都要小于target的话,同样可以直接返回0,因为不可能凑出结果
因为本题要求的是有多少种方式,所以这里将 dp 数组的含义先定义为有多少种方式,而对于这个方式的限定条件有
m:也就是 加法部分 需要达到的和- 可以选取的数组元素的范围。
if ((target + sum) % 2 != 0) return 0;
if ( target < 0 && sum < -target) return 0;
所以可以将 dp[i][j] 定为在只能选取数组的前 i 个元素的情况下,能够凑成 j 的所有方式有多少种。
那这个状态能否发生转移呢?对于一个新的元素来说,同样会出现两种情况:不选取这个元素,还是按照原来的方式来;另一种就是选取这个元素。但这题与背包问题最大的区别就是 背包问题求得的是最优的情况,而本题求得是有多少种组合,所以背包问题需要求得最大值,而本题则采用 加和 的方式,即
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]
💡 这里来说一下数组的第二个部分,也就是
dp[i - 1][j - nums[i]]的情况,如果现在可以取得nums[i]那得到j的方式其实就是dp[i - 1][j - nums[i]]种,也就是装满j - nums[i]有多少种方法,在这个基础上累加一个nums[i]也就是dp[i][j]要求的情况。
其实本题有个比较特殊的情况,就是当 m 为负数的时候,因为 target 可能为负数,最终导致
m = (target + sum) / 2 也是负数的情况,这时候如果去初始化 dp 数组就会出现下标为负数的情况,所以针对这个情况要做特殊的处理,其实这时候只要将 m 取反,然后去将这个值按照新的 m 去做就可以了,那这个数组就变成了达到 -m 的方式有多少种,这和达到 m 的方式有多少种是完全一样的。
<3> 代码
回溯算法
class Solution {int path = 0;int res = 0;public int findTargetSumWays(int[] nums, int target) {backtracking(nums, target, 0);return res;}public void backtracking(int[] nums, int target, int index) {if (path == target && index == nums.length) {res++;return;}if (index == nums.length) {return;}for (int i = 0; i < 2; i++) {if (i == 0) {path += nums[index];backtracking(nums, target, index + 1);path -= nums[index];} else {path -= nums[index];backtracking(nums, target, index + 1);path += nums[index];}}}
}
动态规划
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i : nums) sum += i;if ((target + sum) % 2 != 0) return 0;if ( target < 0 && sum < -target) return 0;int m = (target + sum) / 2; if(m < 0) m = -m; // 处理负值的情况int[] dp = new int[m + 1]; dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = m; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[m]; }
}
03. 一和零(No. 474)
题目链接
代码随想录题解
<1> 题目
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ,因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = [“10”, “0”, “1”], m = 1, n = 1
输出:2
解释:最大的子集是 {“0”, “1”} ,所以答案是 2 。
提示:
1 <= strs.length <= 6001 <= strs[i].length <= 100strs[i]仅由'0'和'1'组成1 <= m, n <= 100
<2> 笔记
本题其实是背包问题的一种变式,将背包问题 背包容量的 一维拓展到了二维;本题中同时限制了两个方向,就是 0 的个数和 1 的个数,所以很简单的思路就是将数组拓展到三维数组,但这样拓展会使得代码编写和理解较为困难,所以想到了使用滚动数组,这样只需要书写二维数组就可以了。
这参考的是 01 背包的滚动数组方法,可以去看一下我的这篇博客:
代码随想录刷题笔记 DAY 42 | 背包问题 - 二维 | 背包问题 - 一维 | 分割等和子集 No.416
因为采用的是滚动数组,所以遍历方向是 从后往前 的
for (int i = m; i >= zero; i--) {for (int j = n; j >= one; j--) {}
}
然后在外层去遍历数组(物品)。
因为题目中求得的是最大子集的长度,所以 dp 数组的定义要尽量往这个方向去靠近,也就是在 n 个字符串中选取得到的子集含有的最多元素数是多少。
dp[i][j] 其实就是要不要加上这个元素,不加上的话就是 dp[i][j] 因为是滚动数组,加上的话就是 dp[i - zero][j - one] + 1 注意这里有两个限制条件。
卡哥最后的总结我非常喜欢,这里来引用一下,我做题的时候确实没有思考到这些:
不少同学刷过这道题,可能没有总结这究竟是什么背包。
此时我们讲解了0-1背包的多种应用,
- 纯 0 - 1 背包 (opens new window)是求 给定背包容量 装满背包 的最大价值是多少。
- 416. 分割等和子集 (opens new window)是求 给定背包容量,能不能装满这个背包。
- 1049. 最后一块石头的重量 II (opens new window)是求 给定背包容量,尽可能装,最多能装多少
- 494. 目标和 (opens new window)是求 给定背包容量,装满背包有多少种方法。
- 本题是求 给定背包容量,装满背包最多有多少个物品。
所以在代码随想录中所列举的题目,都是 0-1背包不同维度上的应用,大家可以细心体会!
<3> 代码
class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m + 1][n + 1];for (String s : strs) {int one = getNum(s)[0];int zero = getNum(s)[1];for (int i = m; i >= zero; i--) {for (int j = n; j >= one; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zero][j - one] + 1);}}}return dp[m][n];}public int[] getNum(String s) {int m = 0;int n = 0;char[] charArray = s.toCharArray();for (char c : charArray) {if ('1' == c) m += 1;else n += 1;}return new int[]{m, n};}
}
相关文章:

代码随想录刷题笔记 DAY 42 | 最后一块石头的重量 II No.1049 | 目标和 No.494 | 一和零 No.474
文章目录 Day 4301. 最后一块石头的重量 II(No. 1049)<1> 题目<2> 笔记<3> 代码 02. 目标和(No. 494)<1> 题目<2> 笔记<3> 代码 03. 一和零(No. 474)<1> 题目&l…...
)
793.高精度乘法(acwing)
文章目录 793.高精度乘法题目描述高精度乘法 793.高精度乘法 题目描述 给定两个正整数A和B,请你计算A * B的值。 输入格式 共两行,第一行包含整数A,第二行包含整数B。 输出格式 共一行,包含A * B的值。 数据范围 1≤A的长度≤…...

考研经验|如何从考研失败中走出来?
对我来说,太丢人了 其实我在本科的时候在同学眼中,一直很优秀,每年奖学金必有我的,国家励志奖学金,国家奖学金,这种非常难拿的奖学金,我也拿过,本科期间学校有一个公费去新西兰留学的…...

SpringBoot如何修改pom依赖的默认版本号
1、找到SpringBoot父工程依赖。 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.3.5.RELEASE</version> </parent>2、ctrl 鼠标左键点击<artifact…...

UDP与TCP:了解这两种网络协议的不同之处
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

String、StringBuffer基本用法
一、StringBuffer基本用法 1.append():字符串连接操作 StringBuffer sb new StringBuffer();sb.append("a");sb.append("b");sb.append("c");sb.append("哈哈").append("d");System.out.println(sb);2.insert():在任意位…...

蓝桥杯刷题5--GCD和LCM
目录 1. GCD 1.1 性质 1.2 代码实现 2. LCM 2.1 代码实现 3. 习题 3.1 等差数列 3.2 Hankson的趣味题 3.3 最大比例 3.4 GCD 1. GCD 整数a和b的最大公约数是能同时整除a和b的最大整数,记为gcd(a, b) 1.1 性质 GCD有关的题目一般会考核GCD的性质。 …...

LVS+Keepalived 高可用负载均衡集群
一. 高可用集群的相关知识 1.1 高可用(HA)集群和普通集群的比较 ① 普通集群 普通的群集的部署是通过一台度器控制调配多台节点服务器进行业务请求的处理,但是仅仅是一台调度器,就会存在极大的单点故障风险,当该调度…...
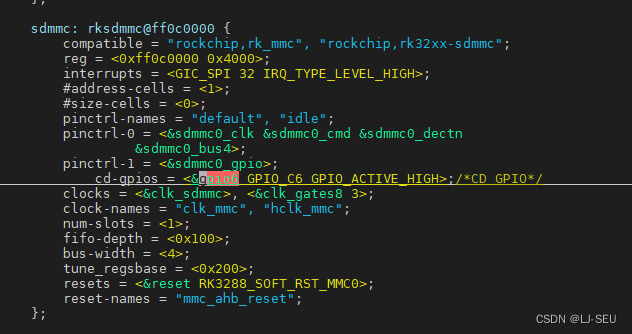
【RK3288 Android6, T8PRO 快捷按键 gpio 配置上拉输入】
文章目录 【RK3288 Android6, T8PRO 快捷按键 gpio 配置上拉输入】需求开发过程尝试找到没有用的上拉gpio尝试修改pwm1的gpio的默认上拉模式 改动 【RK3288 Android6, T8PRO 快捷按键 gpio 配置上拉输入】 需求 T8pro想要模仿T10 的 快捷按键ÿ…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:LoadingProgress)
用于显示加载动效的组件。 说明: 该组件从API Version 8开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 无 接口 LoadingProgress() 创建加载进展组件。 从API version 9开始,该接口支持在ArkTS卡片中使…...

隐私与创新的交汇点:Partisia Blockchain 重绘技术蓝图
正当我们在这个信息泛滥的时代寻找稳固的信任锚点时,区块链技术应运而生,然而,正如任何科技革命都会遇到的挑战,一个重要的问题摆在了我们面前:如何在不牺牲个人隐私的前提下,享受区块链技术带来的好处&…...

小程序 van-field label和输入框改成上下布局
在组件上面加个样式就行:custom-style"display:block;" <van-field label"备注说明" type"textarea" clearable title-width"100px" custom-style"display:block;" placeholder"请输入" /> …...
)
跨域资源共享(CORS)
预检请求 预检请求(Preflight Request)是跨域资源共享(CORS)机制中的一种特殊请求,主要用于在实际请求之前进行安全性检查。当一个请求可能不满足同源策略(即请求的源与目标资源的源不同,源包括…...
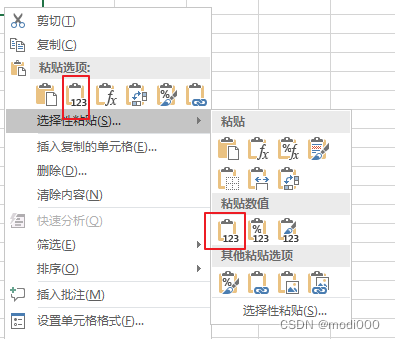
excel中去除公式,仅保留值
1.单个单元格去除公式 双击单元格,按F9. 2.批量去除公式 选中列然后复制,选择性粘贴,选值粘贴...

大数据和数据要素有什么关系?
大数据与数据要素之间存在密切的关系。大数据是指海量、多样化、高速生成的数据,而数据要素是指构成数据的基本元素或属性。数据要素包括但不限于数据的类型、结构、格式、单位、精度等。 大数据的产生和应用离不开数据要素的支持。数据要素确定了数据的基本特征和…...
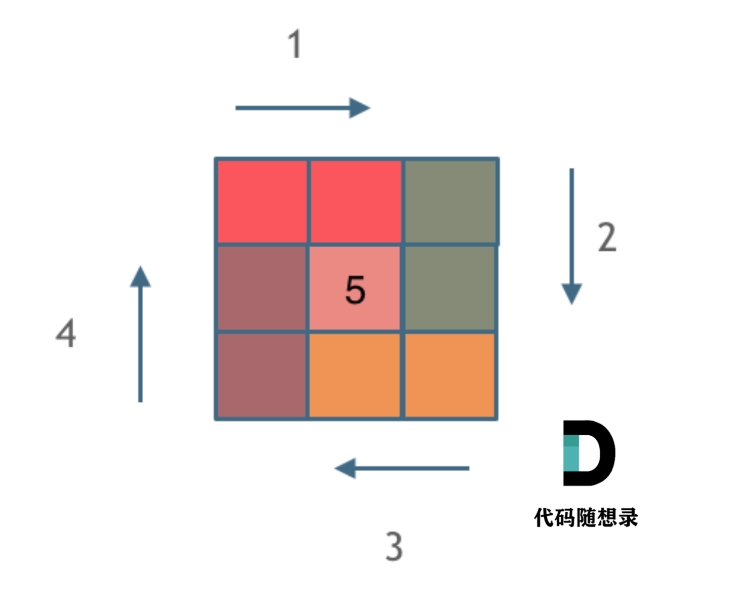
Leetcode 59.螺旋矩阵Ⅱ
1.题目 2.思路 (借用代码随想录的图) 1.我们将转一圈看作一个循环(1->2->3->4->5->6->7->8 这是一个循环) 2.在这个循环里,我们要画四条边(上右下左) 填充上行从左到右 填…...
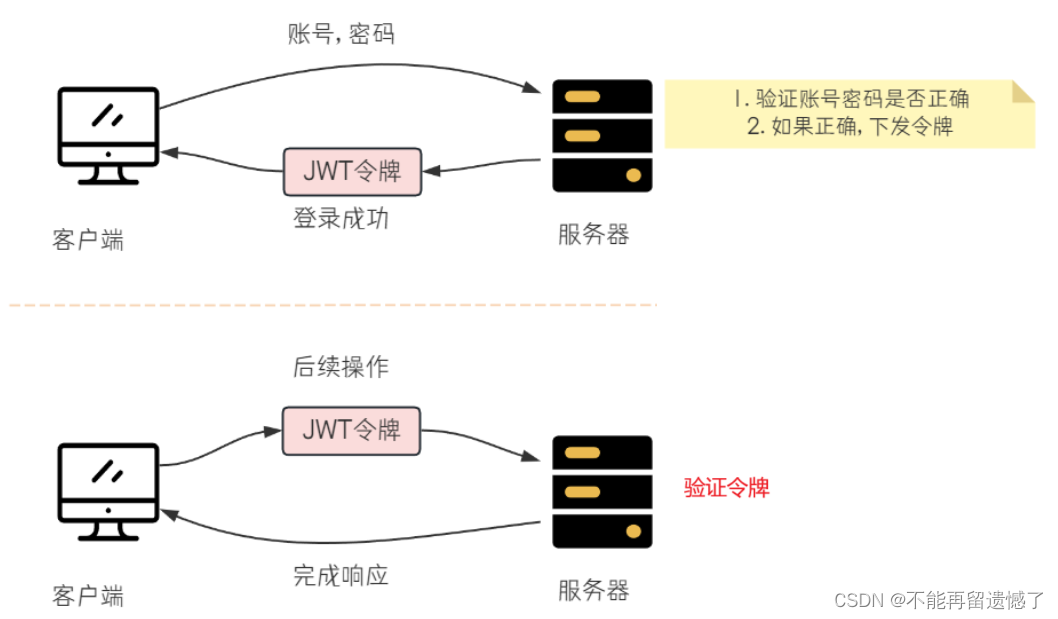
JWT令牌技术
文章目录 什么是令牌技术为什么需要令牌技术呢JWT 令牌JWT 组成JWT 令牌的使用1. 引入 JWT 依赖生成 JWT 令牌解析 JWT 令牌 什么是令牌技术 令牌技术是一种重要的安全技术,它在多个领域中发挥着关键作用。简单来说,令牌(Token)可…...

从零学习Linux操作系统 第三十二部分 ansible中剧本的应用
一、什么是playbook及playbook的组成 1.Playbook的功能 playbook 是由一个或多个play组成的列表 Playboot 文件使用YAML来写的 play就是一个个模块用列表的方式体现出来 playbook的语法是用YAML的预防进行书写的 2.YAML 简介 是一种表达资料序列的格式,类似XM…...
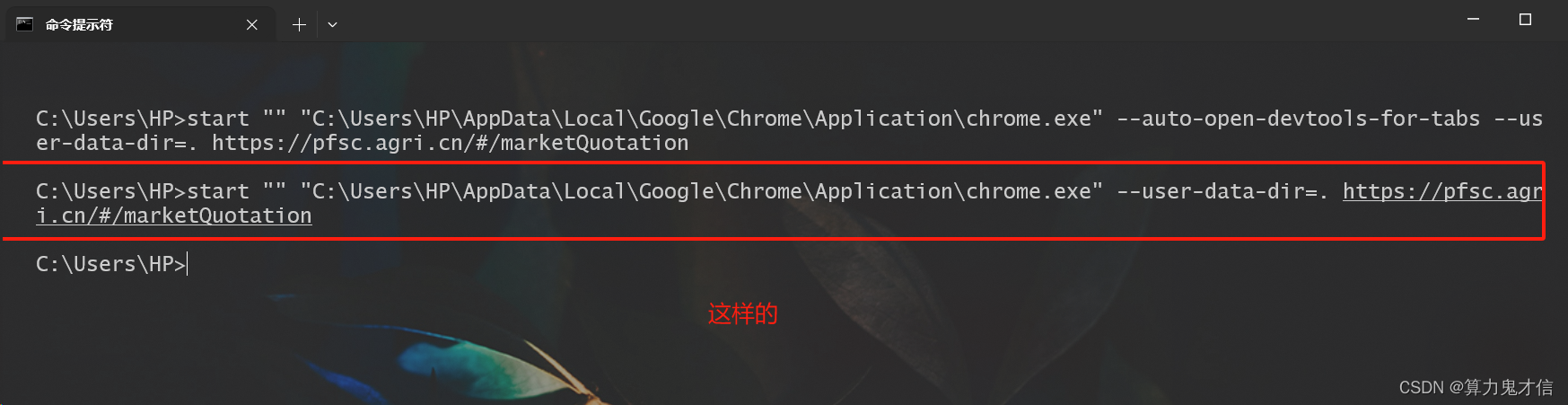
目标网站屏蔽右键检查(使用开发者工具)
问题: 通过网络触手中想要获取某网站的数据出现:鼠标右击,或按ctrl F10 键 无反应(也就是打不开类似谷歌的开发工具) 问题同等与: 解决网页屏蔽F12或右键打开审查元素 引用: 作者ÿ…...
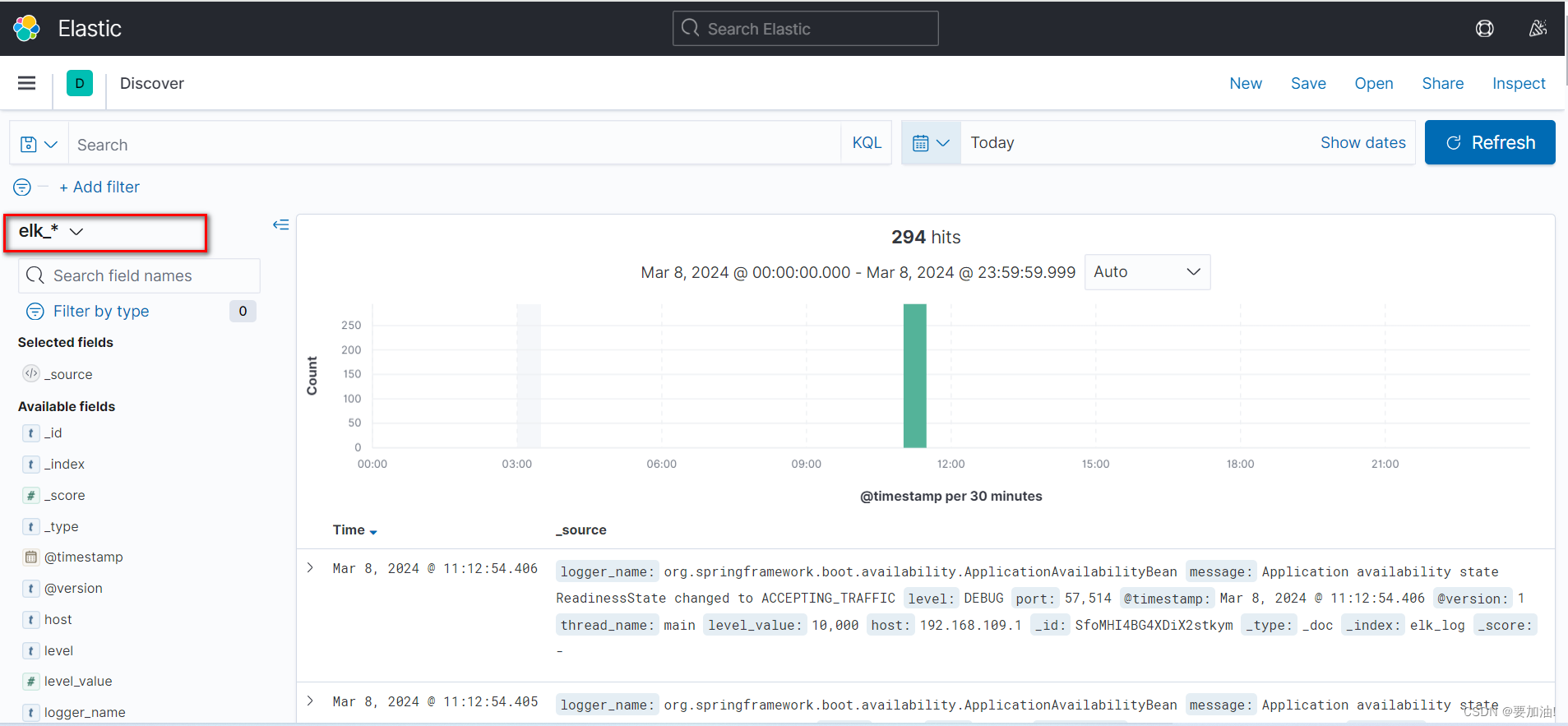
docker安装ES、LogStash、Kibana
文章目录 一、安装Elasticsearch1. 安装Elasticsearch2. 安装IK分词器3. elasticsearch-head 监控的插件4. 配置跨域 二、安装LogStash三、安装kibana四、SpringBoot集成LogStash,将日志输出到ES中五、 启动项目,监控项目运行 提示:以下是本篇…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
