算法中的数学知识
文章目录
- 算法中的数学知识
- 约数
- 约数个数
- 约数之和
- 筛法求质数
- 阶乘分解
- 解法一
- 解法二:
- 欧拉函数
- 基本模板
- 筛法求欧拉函数
- 大数据幂的欧拉函数
- 快速幂
- 费马小定理
- 快速幂求逆元
- 数论分块
- 例题:[因数平方和](https://www.acwing.com/problem/content/4665/)
- 分析:
- 具体代码:
- __int128写法
- 逆元写法
- 例题2:余数之和
- 高斯消元法
- 算法步骤
- 组合数学
- 题型一
- 题型二
- 题型三(卢卡斯定理)
- 卡特兰数
- 889. 满足条件的01序列
- 129.火车进站问题
- 130.火车进出栈问题
算法中的数学知识
约数

约数个数
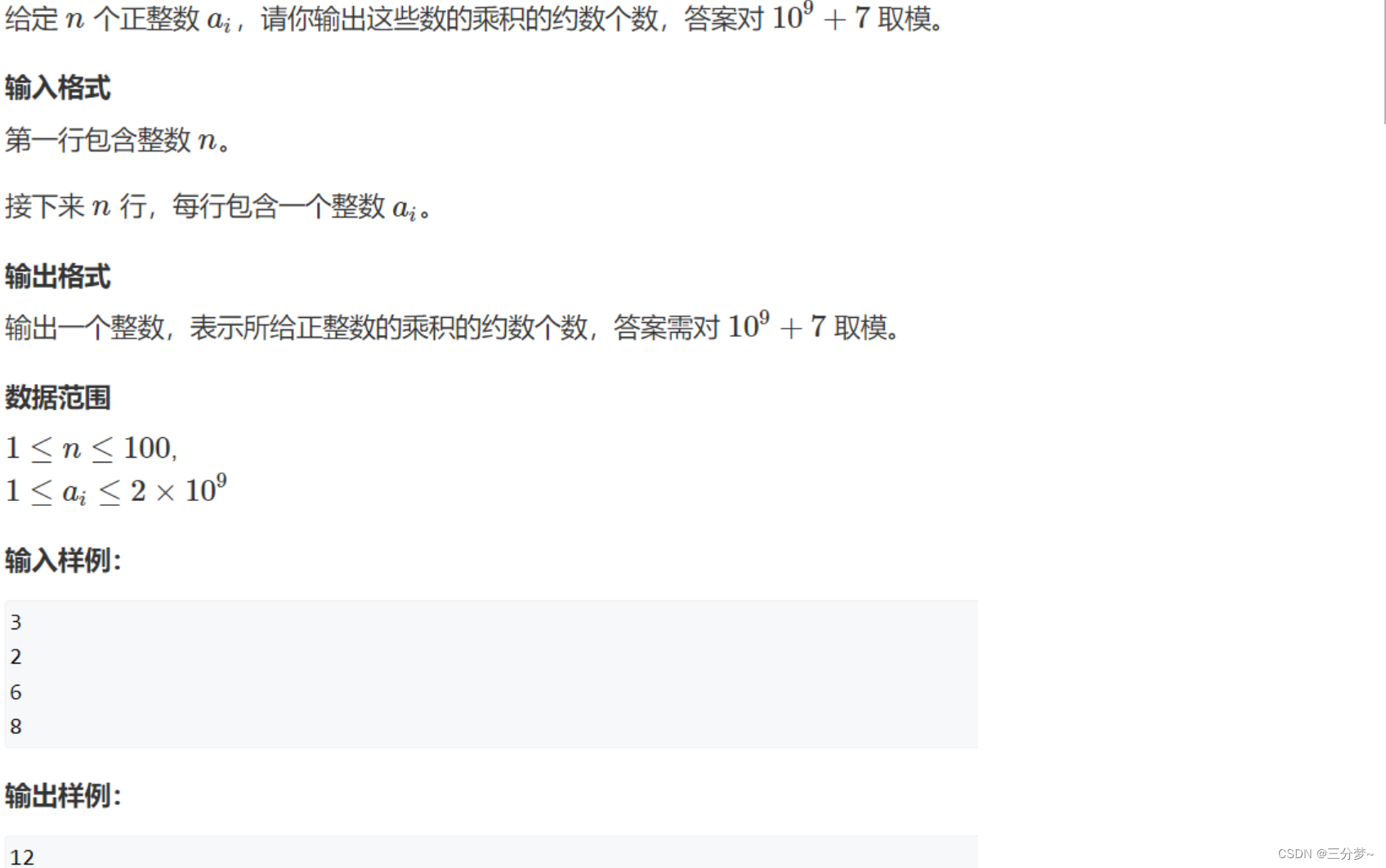
原题链接:约束个数
代码如下:
#include <iostream>
#include <unordered_map>
#include <algorithm>
using namespace std;
const int N = 110, mod = 1e9 + 7;
int main() {int n;cin >> n;unordered_map<int, int> primes; //分别存储质因子的底数和指数while(n--) {int x;cin >> x;for(int i = 2; i <= x / i; i++) {while(x % i == 0) {x /= i;primes[i]++;}}if(x > 1) primes[x]++;}long long res = 1;for(auto prime : primes) res = res * (prime.second + 1) % mod;cout << res;return 0;
}
约数之和
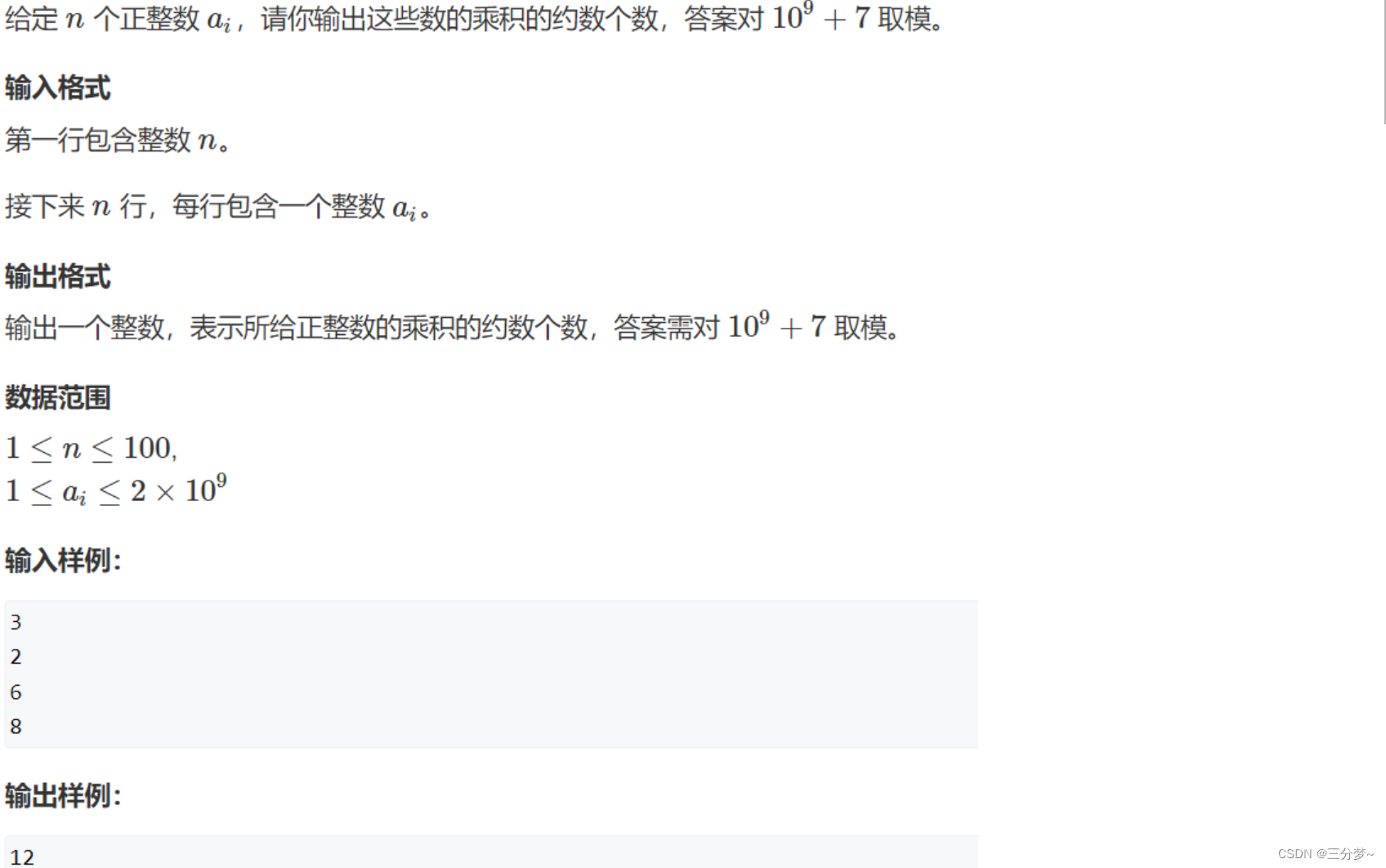
原题链接:约数之和
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
int main() {int n;cin >> n;unordered_map<int, int> primes;while(n--) {int x;cin >> x;for(int i = 2; i <= x / i; i++) {while(x % i == 0) {x /= i;primes[i]++;}}if(x > 1) primes[x]++;}long long res = 1;for(auto prime : primes) {long long t = 1;while(prime.second --)t = (prime.first * t + 1) % mod;res = res * t % mod;}cout << res;return 0;
}
筛法求质数
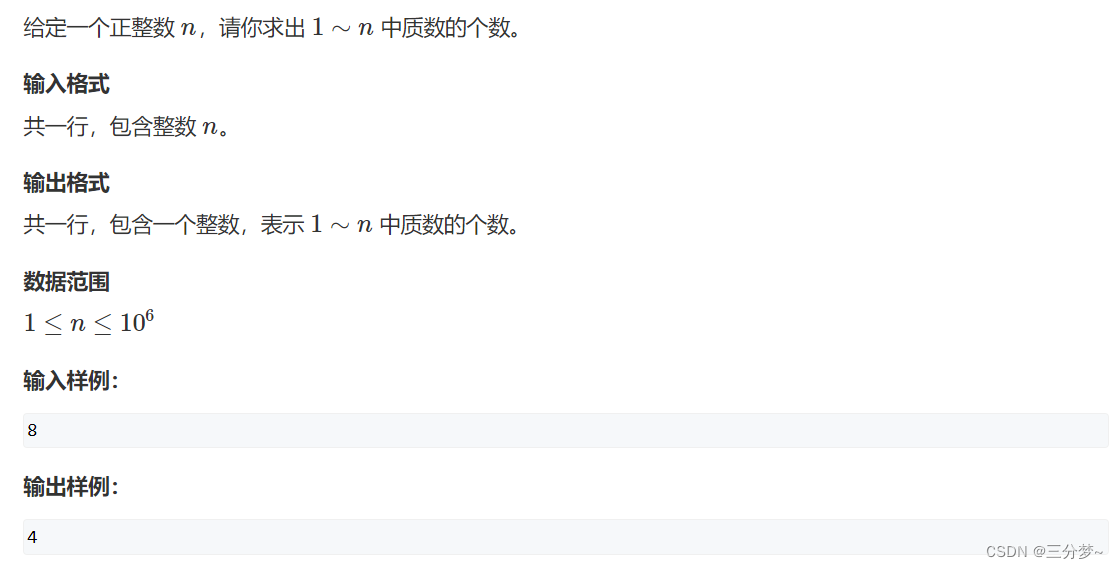
原题链接:筛质数
每次从最小质数开始遍历,可以保证n只会被最小质数筛到, 避免多次筛到, 每个数只会被筛一次, 即时间复杂度为 O ( n ) O(n) O(n), 线性筛法
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int primes[N];
bool st[N];
int n;
int get_primes(int n) {if(n < 2) return 0;int cnt = 0;for(int i = 2; i <= n; i++ ) { //一次线性筛选,即可完成操作if(!st[i]) primes[cnt++] = i; //没被筛到,则为质数for(int j = 0; primes[j] * i <= n; j++) {st[primes[j] * i] = true; //从最小质数集开始筛选相关合数if(i % primes[j] == 0) break; //找到最小质因数,直接操作结束}}return cnt;
}
int main() {cin >> n;cout << get_primes(n);return 0;
}
阶乘分解
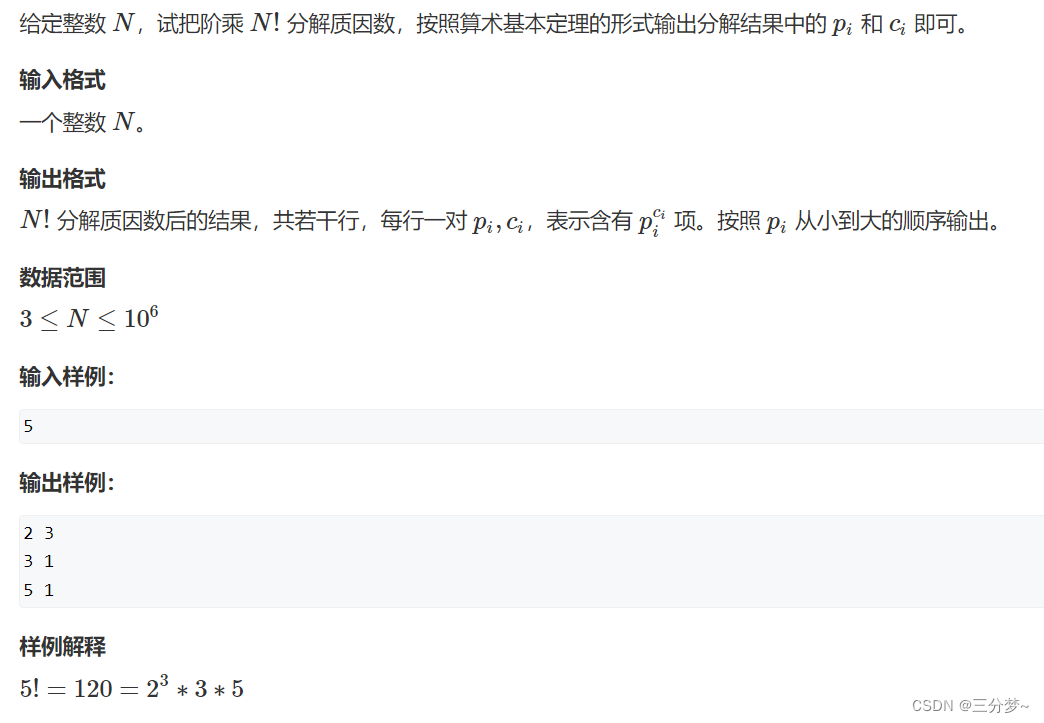
题目链接:https://www.acwing.com/problem/content/description/199/
解法一
思路分析:

先用线性筛法求出质数数组,随后对每个质数进行操作
a n s = ∑ p r i m e s [ i ] n n p + n p 2 + n p 3 + … ans = \sum_{primes[i]}^{n} \frac{n}{p} + \frac{n }{p^2} + \frac{n}{p^3} + … ans=∑primes[i]npn+p2n+p3n+…
代码
//思路:将质数最小到大进行枚举,直接通过“倍数”[n/p]来计算相应次数,然而[1,n]中
//有的数含的p的次数不止一次,故进行[n/p] + [n / p^2] + [n / p^3] + ...
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int primes[N], cnt = 0;
bool st[N];
void get_primes(int n) {for(int i = 2; i <= n; i++) { //枚举1~n中的所有筛选质数if(!st[i]) primes[cnt++] = i; //若没有被筛掉,则为质数for(int j = 0; primes[j] * i <= n; j++) {st[primes[j] * i] = true;if(i % primes[j] == 0) break;}}
}int main() {int n;cin >> n;get_primes(n); //先初始化primes数组//然后进行枚举各个质数算出次数for(int i = 0; i < cnt; i++) {int p = primes[i]; //质数int t = n, ct = 0;while(t) ct += t / p, t /= p; //每次的t/=p,下一次就成了cnt += t/p^2printf("%d %d\n", primes[i], ct);}}
解法二:
思路同上
#include <bits/stdc++.h>
using namespace std;
int n;
bool prime(int x) {if (x == 2) return 1;for (int i = 2; i * i <= x; i++) if (x % i == 0) return 0;return 1;
}
int main() {scanf("%d", &n);for (int i = 2; i <= n; i++) {if (!prime(i)) continue;long long x = i; int ans = 0;while (x <= n) ans += n / x, x *= i;printf("%d %d\n", i, ans);}return 0;
}
欧拉函数
基本模板
原题链接:欧拉函数


#include <iostream>
#include <unordered_map>
using namespace std;
int euler(int x) {int res = x;for(int i = 2; i <= x / i; i++) {if(x % i == 0) {res = res / i * (i - 1);while(x % i == 0) x /= i;}}if(x > 1) res = res / x * (x - 1);return res;
}int main() {int n;cin >> n;while(n --) {int a;cin >> a;cout << euler(a) << endl;}return 0;
}
筛法求欧拉函数
原题链接
代码如下:
//欧拉:1 ~ n - 1 中与n互质的数的个数
#include <iostream>
#include <bitset>
using namespace std;
const int N = 1e6 + 10;
int primes[N], cnt;
int phi[N];
bitset<N> st;
long long get_eulers(int n) {long long res = 0;phi[1] = 1;for(int i = 2; i <= n; i++) { //线性筛法,遍历一次nif(!st[i]) { //没有被筛,质数primes[cnt++] = i;phi[i] = i - 1; //若为质数,则代表1 ~ i - 1都为互质}for(int j = 0; primes[j] <= n / i; j++) {st[primes[j] * i] = 1;if(i % primes[j] == 0) {//若primes[j]为i的质因数,则有 primes[j] 的质因子必然存在于i中phi[i * primes[j]] = primes[j] * phi[i];break;}//若i % primes[j] != 0,则对质数primes[j]另行计算有:p[j] * (p[j] - 1) / p[j]phi[i * primes[j]] = phi[i] * (primes[j] - 1);}}for(int i = 1; i <= n; i++) res += phi[i];return res;
}
int main() {int n;cin >> n;cout << get_eulers(n); return 0;
}
大数据幂的欧拉函数
原题链接:互质数的个数
分析:
如上图可以将 ϕ ( a b ) \phi(a^b) ϕ(ab)分解为 a b ∗ ϕ ( a ) a^b*\phi(a) ab∗ϕ(a), 继续演变为求欧拉和快速幂的结合应用
*** 代码如下:***
#include <iostream>
using namespace std;
const int MOD = 998244353;
long long qmi(long long a, long long b) {long long res = 1;while(b) {if(b & 1) res = res * a % MOD;a = a * a % MOD;b >>= 1;}return res;
}
int main() {long long a, b;cin >> a >> b;if(a == 1) { //题目要求是x不能取到a^b, 故如果a=1,互质个数为0cout << 0 << endl;return 0;}long long res = a, x = a;for(int i = 2; i <= x / i; i++) {if(x % i == 0) {res = res / i * (i - 1);while(x % i == 0) x /= i;}}if(x > 1) res = res / x * (x - 1);cout << res * qmi(a, b - 1) % MOD << endl;return 0;
}
快速幂
基本思想:
将 a k a^k ak化为 a 2 x 1 ∗ a 2 x 2 ∗ a 2 x 3 ∗ . . . ∗ a 2 x t a^{2x~1~}*a ^{2x~2~} * a^{2x~3} * ...*a^{2x~t~} a2x 1 ∗a2x 2 ∗a2x 3∗...∗a2x t
***本质:***将k化为若干个2的次幂之和
这时候可以想到用二进制来操作
例如:若 k = 1101010 < = = > <==> <==> 2 1 + 2 3 + 2 5 + 2 6 2^1 + 2^3 + 2^5 + 2^6 21+23+25+26
对二进制位数进行遍历, 当k & 1 == 1,即当前k的最后一个位置为1,进行累乘
代码如下:
#include <iostream>
using namespace std;
typedef long long LL;
// a^k % p
int qmi(int a, int k, int p) {int res = 1;//本质:将k拆分为2的n次幂之和while(k){ if(k & 1) res = (LL)res * a % p;k >>= 1;a = (LL)a * a % p; }return res;
}int main() {int n;cin >> n;while(n-- ) {int a, b, p;scanf("%d%d%d", &a, &b, &p);cout << qmi(a, b, p) << endl;}return 0;
}
费马小定理
a p 与 a 在 m o d ( p ) 的情况下是同余的 a^p与a在mod(p)的情况下是同余的 ap与a在mod(p)的情况下是同余的

快速幂求逆元
快速幂求逆元

**分析:**只需求出 b p − 2 % p b^{p-2}\ \%\ p bp−2 % p的快速幂即可
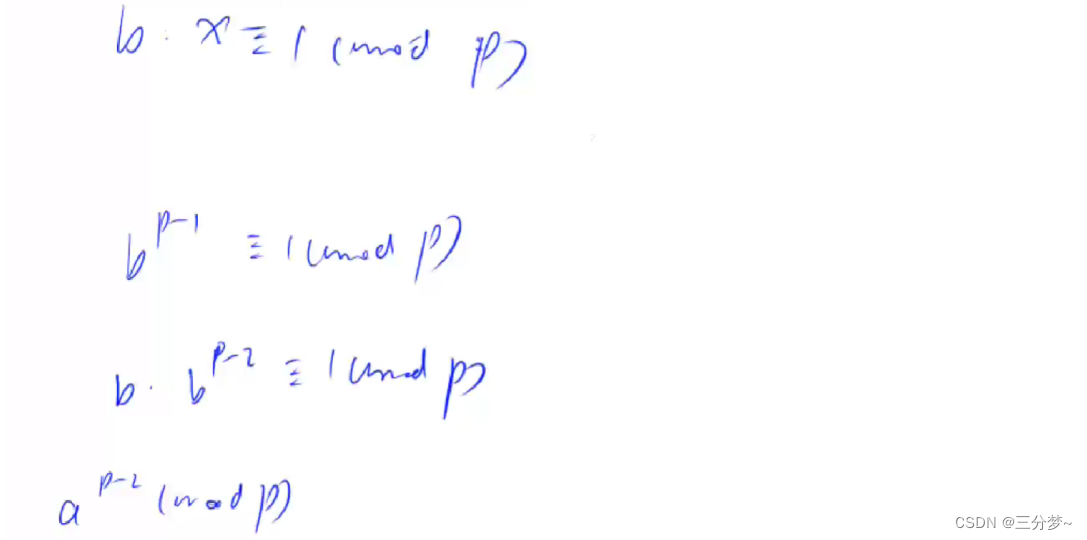
代码如下:
#include <iostream>
using namespace std;
typedef long long LL;int qmi(int a, int k, int p) {int res = 1;while(k) {if(k & 1) res = (LL)res * a % p;k >>= 1;a = (LL)a * a % p;}return res;
}
int main() {int n;cin >> n;while(n-- ) {int a, p;scanf("%d%d", &a, &p);if(a % p == 0) cout << "impossible" << endl;else cout << qmi(a, p - 2, p) << endl;}return 0;
}
数论分块

一般在算法中遇到时间复杂度为
1e9的, 那么一次 O ( n ) O(n) O(n)的遍历无法解决问题
求··· ∑ i = 1 n [ n i ] \sum_{i=1}^n{[\frac{n}{i}]} ∑i=1n[in]···



例题:因数平方和

分析:
要求 n n n的约数,时间复杂度肯定不够, 所以想到反着求
a是b的约数 <==> b是a的倍数,所以我们只需要求哪些数包含约数a相加
每一个约数a 对答案的贡献度为 a 2 a^2 a2, 每个数a是 n a \frac{n}{a} an个数的约数
故a这个数对答案的总贡献为 a 2 ∗ [ n a ] a^2\ *\ [\frac{n}{a}] a2 ∗ [an],故答案为:
∑ i = 1 n [ n i ] ∗ i 2 \sum_{i=1}^n\ [\frac{n}{i}]*i^2 i=1∑n [in]∗i2

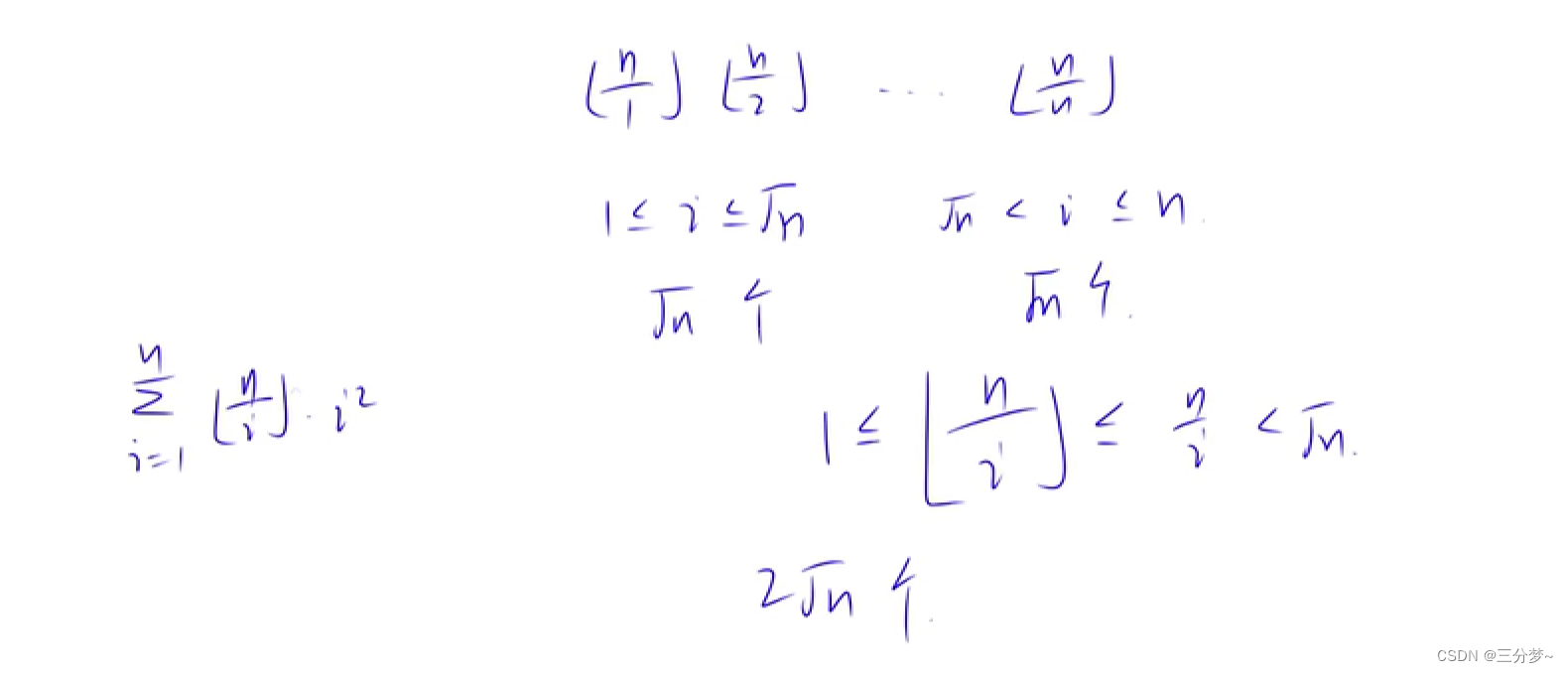
由上可知, 可以将n划分为前半段和后半段的话, 可计算出只需操作 2 n 2\sqrt{n} 2n个数即可
如此, 可以将 n n n优化为 2 n 2\sqrt{n} 2n个数进行计算
进行分块治理,如下
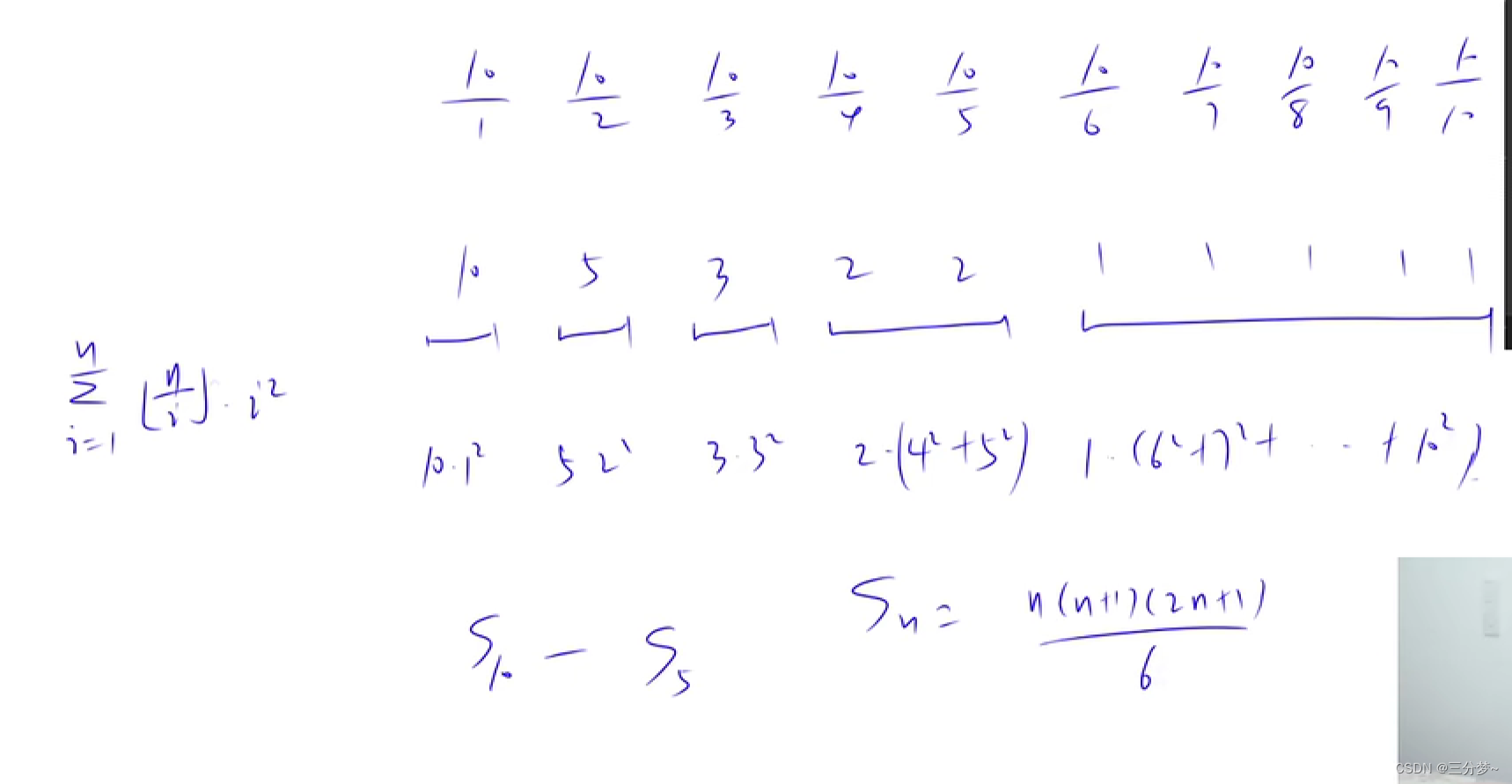
将区间长度为 n n n划分为 2 n 2\sqrt{n} 2n个区间, 对每个区间进行求值,每个区间值相同, 只需算连续平方和,可以直接用公式求平方和值, 故每个区间只需要算一次即可
结果: O ( N ) − − > O ( N 2 ) O(N) - - > O(N^2) O(N)−−>O(N2)

推导出:每个区间最大的位置: y = n / x y = n / x y=n/x , 对于各个区间值为== x = n / i x = n / i x=n/i==
即计算区间和每个== [ i , y ] [i, y] [i,y]区间即可, 然后算完一个区间直接 i = y + 1 i = y + 1 i=y+1,来跳跃到下一个区间进行计算, 总共只需要算 2 n 2\sqrt{n} 2n==次
具体代码:
此题在计算平方和时可能数据量会超大(超LL)
__int128写法
#include <iostream>
using namespace std;
const int MOD = 1e9 + 7;
typedef long long LL;
//__int128 : 2^127 - 1
LL calc(int n) { //计算平方和
//这里可能特别大超过2^64(LL),故用__int128临时存储数值return n * (__int128)(n + 1) * (2*n + 1) / 6 % MOD;
}int main() {int n;cin >> n;LL res = 0;for(int i = 1; i <= n; ) {//划分为2sqrt(n)个区间,每个区间的所有数相等,第i个区间值为n/iint x = n / i, y = n / x; //求区间[i, y]的平方和,再乘上x值res = res + x * (calc(y) - calc(i - 1)) % MOD;i = y + 1; }//这块可能取模相减为负值,故cout << (res + MOD) % MOD << endl;return 0;
}
逆元写法
LL calc(int n) { //计算平方和
//这里可能特别大超过2^64(LL),故用__int128临时存储数值// return n * (LL)(n + 1) * (2*n + 1) / 6 % MOD;
//逆元写法return n * (LL)(n + 1) % MOD * (2*n + 1) % MOD * 166666668 % MOD;
}//计算 /6 的逆元
/for(int i = 1; ;i++) { //算出逆元答案为166666668, 带入上式替换掉 '/6'if(i * 6 % MOD == 1) {cout << i << endl;return 0;}
}例题2:余数之和
原题链接

思想:
首先看到数据范围为1e9级别,故可以想到用分块思想,优化到 O ( 2 n ) O(2\sqrt{n}) O(2n)
k % i k \% i k%i <==> k − [ k i ] ∗ i k - [\frac{k}{i}]*i k−[ik]∗i
则 k % ∑ 1 n k \% \sum_1^n k%∑1n < = = > <==> <==> n ∗ k − ∑ i = 1 n [ k i ] ∗ i n*k\ -\ \sum_{i=1}^n[\frac{k}{i}]*i n∗k − ∑i=1n[ik]∗i
代码:
#include <iostream>
using namespace std;
typedef long long LL;
LL sum_primes(int n, int k) {//k % i = k - [k / i] * i ---> k % [1, n] = n*k - k / [1,n]*iLL res = (LL)n * k;for(int i = 1; i <= n; ) {if(k < i) break; //此时往后全为0,不用操作了int x = k / i, y = min(k / x, n); //区间有极限值为n,防止越界//求区间总值 * x --- > 等差数列求和:n * (a1 + an) / 2res -= x * (LL)(y - i + 1) * (i + y) / 2;i = y + 1; //操作下一个区间}return res;
}
int main() {int n, k;cin >> n >> k;cout << sum_primes(n, k) << endl;return 0;
}
高斯消元法
基本性质:
把某一行乘一个非 0 0 0的数 (方程的两边同时乘上一个非 0 0 0数不改变方程的解)
交换某两行 (交换两个方程的位置)
把某行的若干倍加到另一行上去 (把一个方程的若干倍加到另一个方程上去)

算法步骤
枚举每一列c
-
- 找到绝对值最大的一行
-
- 将该行换到最上面
-
- 将该行第1个数变成1
-
- 将下面所有行的第
c列清成0
- 将下面所有行的第
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 110;
double a[N][N];
int n;
const double eps = 1e-8; //浮点型存在精度误差,容易
/*枚举每一列
- 1. 找到绝对值最大的一行
- 2. 将该行换到最上面(第r行)
- 3. 将该行第1个数变成1
- 4. 将下面所有行的第`c`列清成0*/
int gauss() {int c, r;//首先开始枚举每一列进行“清零”操作for(c = 0, r = 0; c < n; c ++) {int mx_r = r;for(int i = r; i < n; i++) //找到绝对值最大的一行if(fabs(a[i][c]) > fabs(a[mx_r][c]))mx_r = i;if(fabs(a[mx_r][c]) < eps) continue; //判断最大如果为0,那么没有算的必要for(int i = c; i <= n; i++) swap(a[mx_r][i], a[r][i]); //换到第r行for(int i = n; i >= 0; i-- ) a[r][i] /= a[r][c]; //第”首位(c)“变为1for(int i = r + 1; i < n; i++ ) {// 将下面所有行的第`c`列清成0if(fabs(a[i][c]) > eps) //若是=0则没必要操作for(int j = n; j >= c; j--)a[i][j] -= a[i][c] * a[r][j]; //a[r][c]为1,故这样可以消0}r++; //该方程式固定好,进行下一个方程式行的操作}//判断无解和无限解的情况if(r < n) { //这样的话,那么说明未知数方程式个数不足n,则无法构成完美梯形for(int i = r; i < n; i++ )if(fabs(a[i][n]) > eps) //多出的答案bi若是不等于0return 2; //无解return 1; //无限解 0 == 0} //进行上三角矩阵的方程化简for(int i = n - 1; i >= 0; i -- ) { //从后往前,anxn = bn,一步一步推前方的方程式未知数for(int j = i + 1; j < n; j++) //每i到最后只需保留第i个数(1),其它数全清零a[i][n] -= a[i][j] * a[j][n]; //这里第j行的答案已经算出,后续数(清零)的同步操作}return 0; //有唯一解
}int main() {cin >> n;for(int i = 0; i < n; i++ )for(int j = 0; j < n + 1; j++ )cin >> a[i][j];int r = gauss();if(r == 0) {for(int i = 0; i < n; i ++) printf("%.2lf\n", a[i][n]);} else if(r == 1) puts("Infinite group solutions");else puts("No solution");return 0;
}
组合数学
题型一

直接算的话会超时
考虑到只有2000 *2000个数,可以直接先打好表
C a b = C a − 1 b − 1 + C a − 1 b C^b_a = C^{b-1}_{a-1} + C^{b}_{a-1} Cab=Ca−1b−1+Ca−1b
代码
#include <iostream>
using namespace std;
const int N = 2010, MOD = 1e9 + 7;
int n;
int c[N][N]; //表示组合数C^b_avoid init() {for(int i = 0; i < N; i++ ) for(int j = 0; j <= i; j++) if(j == 0) c[i][j] = 1;else c[i][j] = c[i - 1][j - 1] % MOD + c[i - 1][j] % MOD;
}int main() {cin >> n;init();while(n --) {int a, b;scanf("%d%d", &a, &b);printf("%d\n", c[a][b] % MOD);}return 0;
}
题型二

时间复杂度高,直接算不行,用集合状态的公式也不行
可以想到如何直接算出fact[N]的表然后套公式打表
C a b = a ! ( b ! ) ∗ ( a − b ) ! C^b_a = \frac{a!}{(b!)*(a - b)!} Cab=(b!)∗(a−b)!a!
由于存在除法,数据量过大需要及时取模,而除法直接取模会导致答案变化,故想到求逆元(费马小定理+快速幂)然后进行相乘
代码如下
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 100010, MOD = 1e9 + 7;
int n;
int fact[N], infact[N]; //分别存储阶乘\阶乘的逆元
int qmi(int a, int b, int p) {int res = 1;while(b) {if(b & 1) res = (LL)res * a % MOD;a = (LL)a * a % MOD;b >>= 1;}return res;
}
void init() {//0的阶乘/逆元阶都为1fact[0] = infact[0] = 1;for(int i = 1; i < N; i++) {fact[i] = (LL)fact[i - 1] * i % MOD;infact[i] = (LL)infact[i - 1] * qmi(i, MOD - 2, MOD) % MOD;}
}int main() {init();cin >> n;while(n-- ) {int a, b;scanf("%d%d", &a, &b);printf("%d\n", (LL)fact[a] % MOD * infact[b] % MOD * infact[a - b] % MOD);}return 0;
}题型三(卢卡斯定理)
公式如下
C a b ≡ C a m o d p b m o d p ∗ C a / p b / p ( m o d p ) C^b_a \equiv C^{b\ mod\ p}_{a\ mod\ p} * C^{b\ /\ p}_{a\ /\ p}\ (mod\ p) Cab≡Ca mod pb mod p∗Ca / pb / p (mod p)
推导

代码:
//发现a,b很大,而p很小,这种情况下用lucas定理来处理
#include <iostream>
using namespace std;
typedef long long LL;
int qmi(int a, int b, int p) {int res = 1;while(b) {if(b & 1) res = (LL)res * a % p;a = (LL)a * a % p;b >>= 1;}return res;
}
int C(int a, int b, int p) {if(b > a) return 0; //!边界条件int res = 1; // a!/(b!(a-b)!) = (a-b+1)*...*a / b!for(int i = 1, j = a; i <= b; i++, j--) {res = (LL)res * j % p;res = (LL)res * qmi(i, p - 2, p) % p;}return res;
}
int lucas(LL a,LL b, int p) {if(a < p && b < p) return C(a, b, p);return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;//a%p后肯定是<p的,所以可以用C(),但a/p后不一定<p 所以用lucas继续递归
}
int main() {int n;cin >> n;while(n--) {int p;LL a, b;cin >> a >> b >> p;printf("%d\n", lucas(a, b, p));}return 0;
}
卡特兰数
889. 满足条件的01序列
题目链接:https://www.acwing.com/problem/content/891/
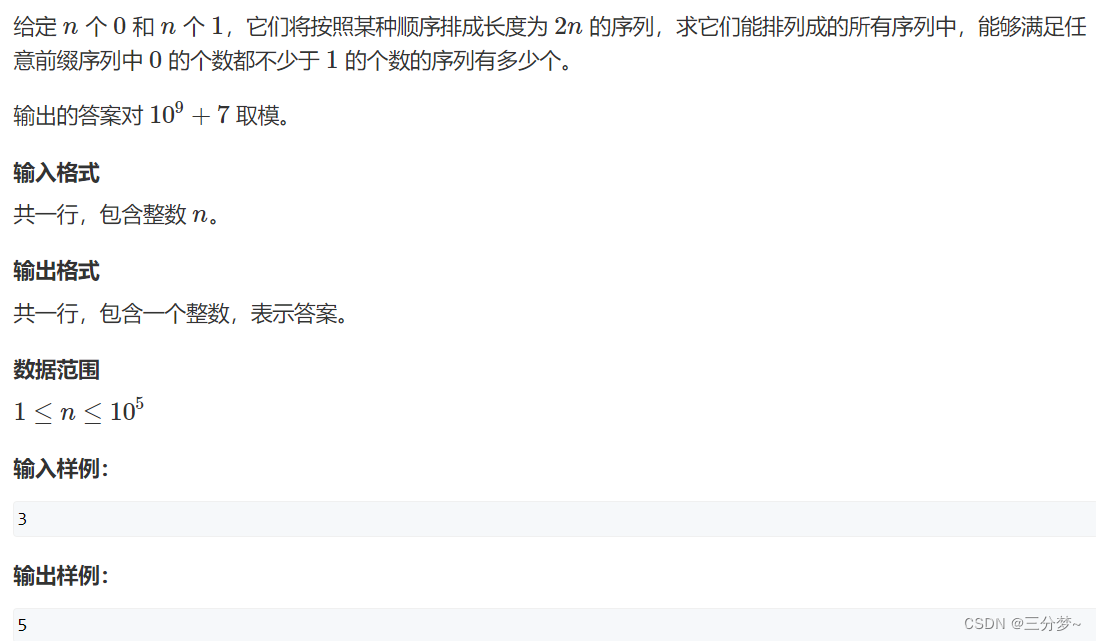
题目思路:
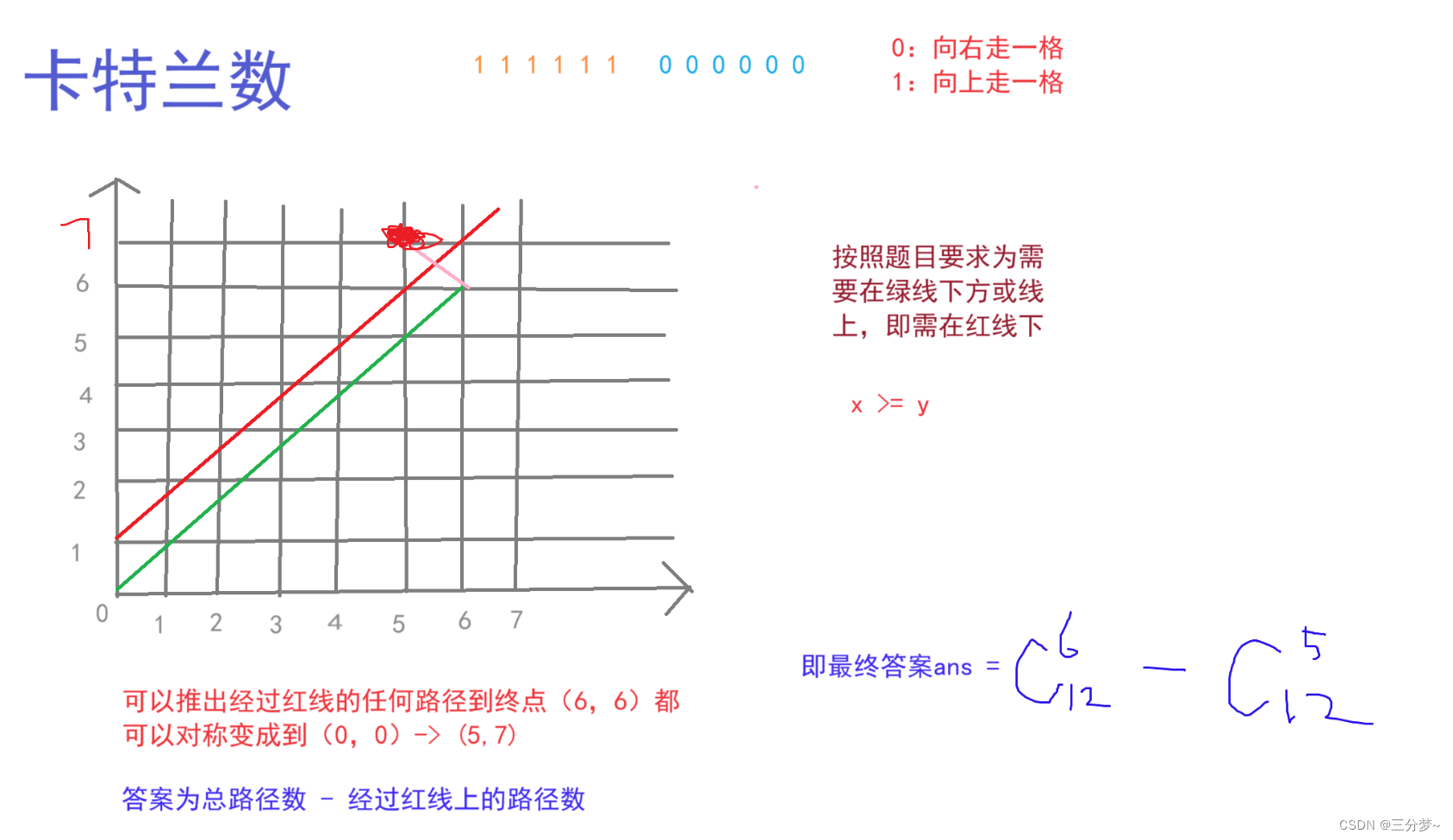
通过以上举例n=6时的情况,可以推出最终:
a n s = C 2 n n − C 2 n n − 1 ans = C_{2n}^n\ -\ C_{2n}^{n-1} ans=C2nn − C2nn−1
又可化简为:
C 2 n n − C 2 n n − 1 = C 2 n n n + 1 C_{2n}^n\ -\ C_{2n}^{n-1} = \frac{C_{2n}^n}{n+1} C2nn − C2nn−1=n+1C2nn
代码实现:
#include <iostream>
using namespace std;
const int MOD = 1e9 + 7;
typedef long long LL;
//用卡特兰公式: ans = (c^n_2n) / (n + 1)
int qmi(int a, int b, int p) {int res = 1;while(b) {if(b & 1) res = (LL)res * a % p;a = (LL)a * a % p;b >>= 1;}return res;
}int main() {int n;cin >> n;int res = 1;// res = [(2n)! / (n! * n!)] / (n + 1)for(int i = 2 * n; i > 2*n - n; i--) res = (LL)res * i % MOD;for(int i = 1; i <= n; i++) res = (LL)res * qmi(i, MOD - 2, MOD) % MOD;res = (LL)res * qmi(n + 1, MOD - 2, MOD) % MOD;cout << res;return 0;
}
129.火车进站问题
原题链接:https://www.acwing.com/problem/content/131/

输入样例:
3
输出样例:
123
132
213
231
321
代码
#include <iostream>
#include <vector>
#include <stack>
#define end '\n'
using namespace std;
vector<int> path;
stack<int> stk;
int n, remain = 20;
void dfs(int u) {if(remain == 0) return ;if(path.size() == n) {remain --; //剩余输出量for(auto t : path)cout << t;cout << endl;return ;}//两种操作选择//1. 出栈操作if(!stk.empty()) { path.push_back(stk.top());stk.pop();dfs(u); //从1开始进行枚举//恢复操作stk.push(path.back());path.pop_back();}//2. 入栈操作if(u <= n) {stk.push(u);dfs(u + 1);//恢复操作stk.pop();}
}
int main() {cin >> n;dfs(1);return 0;
}
130.火车进出栈问题
原题链接:https://www.acwing.com/problem/content/132/
相关文章:

算法中的数学知识
文章目录 算法中的数学知识约数约数个数约数之和 筛法求质数阶乘分解解法一解法二: 欧拉函数基本模板筛法求欧拉函数大数据幂的欧拉函数 快速幂费马小定理快速幂求逆元数论分块例题:[因数平方和](https://www.acwing.com/problem/content/4665/)分析:具体…...
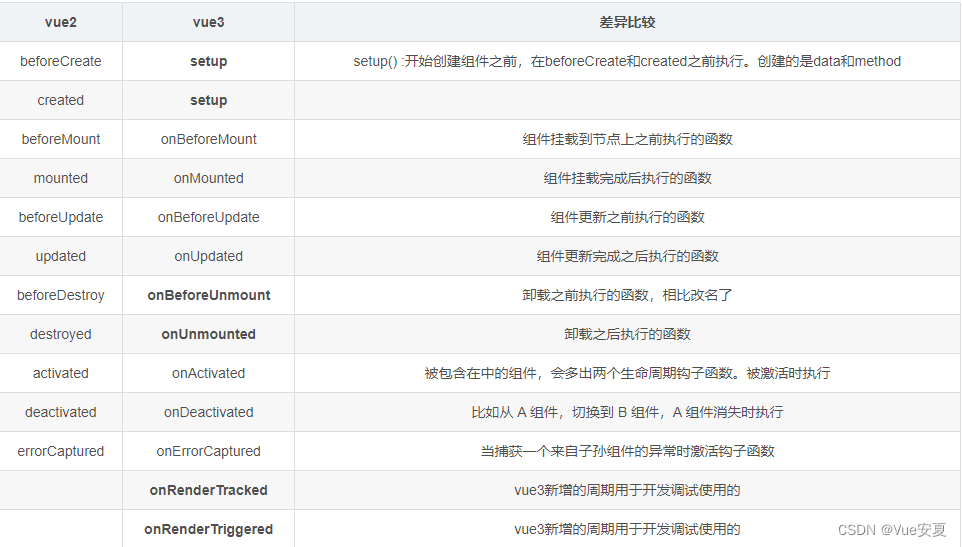
2024高频前端面试题 Vue2 和 Vue3 篇
HTML和CSS篇:2024高频前端面试题 HTML 和 CSS 篇-CSDN博客 JavaScript 和 ES6 篇: 2024高频前端面试题 JavaScript 和 ES6 篇-CSDN博客 * Vue2 和 Vue3的区别: 1)双向数据绑定原理的区别 2)根节点的不同 Vue2只能一…...

vue,Promise备忘
网址 https://www.promisejs.org/ 记录 在Vue.js或者其他JavaScript项目中,Promise 是一种处理异步操作的标准机制,用于解决传统的回调地狱问题,提供了一种更优雅、链式调用的编程模型。Promise对象代表一个异步操作的结果,它可…...
)
软件测试工程师职位笔试知识点细节(2)
一、软件测试分为哪几个阶段,生命周期? 软件测试一般分为单元测试、集成测试和系统测试。 需求分析→测试计划→测试设计、软件开发→测试执行→测试评估 二、一条软件缺陷(或者叫Bug)记录都包含了哪些内容? 一条Bug…...
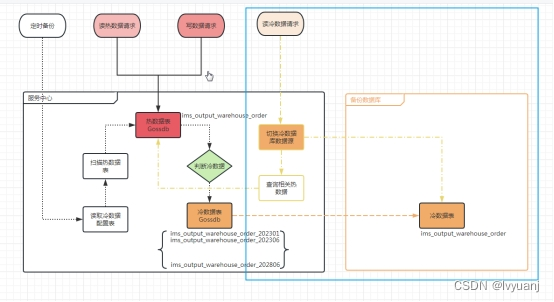
大数据冷热分离方案
数据冷热分离方案 1、背景 随着业务的发展,在线表中的数据会逐渐增加。常规业务都有冷热数据现象明显的特性(需要访问的都是近期产生的热数据;时间久远的冷数据出于备份、备案溯源等诉求会进行在线保留)。在业务表数据 量可控…...

Vue3中Vue Router的使用区别
在 Vue 3 中,useRouter 和 useRoute 是两个用于 Vue Router 的 Composition API 函数,它们的用途和返回的对象不同,接下来详细了解一下它们的区别以及如何正确使用它们。 useRouter useRouter 用于获取 router 实例,这个实例提供…...

Open CASCADE学习|读取STEP模型文件到XDE中
目录 1、XDE组件简介 2、读取STEP模型文件到XDE中的步骤 3、案例 1、XDE组件简介 Open CASCADE的XDE(扩展数据交换)组件是一个关键的工具,它允许用户通过转换附加到几何BREP(边界表示)数据的附加数据来扩展数据交换…...

flink:自定义数据分区
shuffle随机地将数据分配到下游的子任务。 rebalance用round robbin模式将数据分配到下游的子任务。 global把所有的数据都分配到一个分区。 partitionCustom: 自定义数据分区。 package cn.edu.tju.demo; import org.apache.flink.api.common.functions.; import org.apache…...

力扣图论篇
以下思路来自代码随想录以及官方题解。 文章目录 797.所有可能的路径200.岛屿数量130.被围绕的区域1020.飞地的数量 797.所有可能的路径 给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不…...

图腾柱PFC工作原理:一张图
视屏链接: PFC工作原理...
MongoDB开启事务
MongoDB开启事务 配置单节点。到路径C:\Program Files\MongoDB\Server\4.0\bin 使用记事本以管理员权限打开文件mongod.cfg添加如下配置: replication:replSetName: rs02. 重启MongoDB服务 3. 重启后执行命令 rs.initiate()...
风车IM即时通讯系统APP源码DJ2403版完整苹果安卓教程
关于风车IM,你在互联网上能随便下载到了基本都是残缺品, 经过我们不懈努力最终提供性价比最高,最完美的版本, 懂货的朋友可以直接下载该版本使用,经过严格测试,该版本基本完美无缺。 1.宝塔环境如下: Ngin…...

新增流计算计数窗口,TDengine 3.2.3.0 八大板块功能更新
自发布以来,TDengine 3.0 版本在研发人员和社区用户的共同努力下不断优化,产品的稳定性和易用性获得了大幅提升,在知轮科技的智慧轮胎系统、黑格智能 3D 打印业务、韵达快递业务、中国地震台网中心、中移物联智慧出行场景等众多企业项目中获得…...
【架构笔记3】做“用心”之人
凡事就怕“用心”二字,但是用心做事,其实如果没有前提和详情,这本就是一句正确的废话,在一些项目开发和落地过程中,我也有了一些新的体会,自认为不是多余。 我觉得心这个词至少包含四个含义:“…...

前端加密面面观:常见场景与方法解析
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

突破编程_前端_JS编程实例(目录导航)
1 开发目标 目录导航组件旨在提供一个滚动目录导航功能,使得用户可以方便地通过点击目录条目快速定位到对应的内容标题位置,同时也能够随着滚动条的移动动态显示当前位置在目录中的位置: 2 详细需求 2.1 标题提取与目录生成 组件需要能够自…...

扩展学习|系统理解数字经济
文献来源:[1]肖静华,胡杨颂,吴瑶.成长品:数据驱动的企业与用户互动创新案例研究[J].管理世界,2020,36(03):183-205.DOI:10.19744/j.cnki.11-1235/f.2020.0041. [2]陈晓红,李杨扬,宋丽洁等.数字经济理论体系与研究展望[J].管理世界,2022,38(02):208-22413…...

前端学习之列表标签
目录 有序列表 结果 无序标签 结果 数据标签 结果 有序列表 (注:注释是解释) <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Document</title> </…...
)
华为OD面试分享14(2024年)
双非本,机试400分,部门流程与IT,base西安 分享面经攒人品 10.27 一面 深挖项目,面试官很友好,根据项目的每个技术点和场景来提问,比如项目中数据库数据量级有多大,什么时候会出现缓慢,如何解决的,有没有经过压力测试,经过优化后性能怎么样,项目中用到的Kafka和redis…...
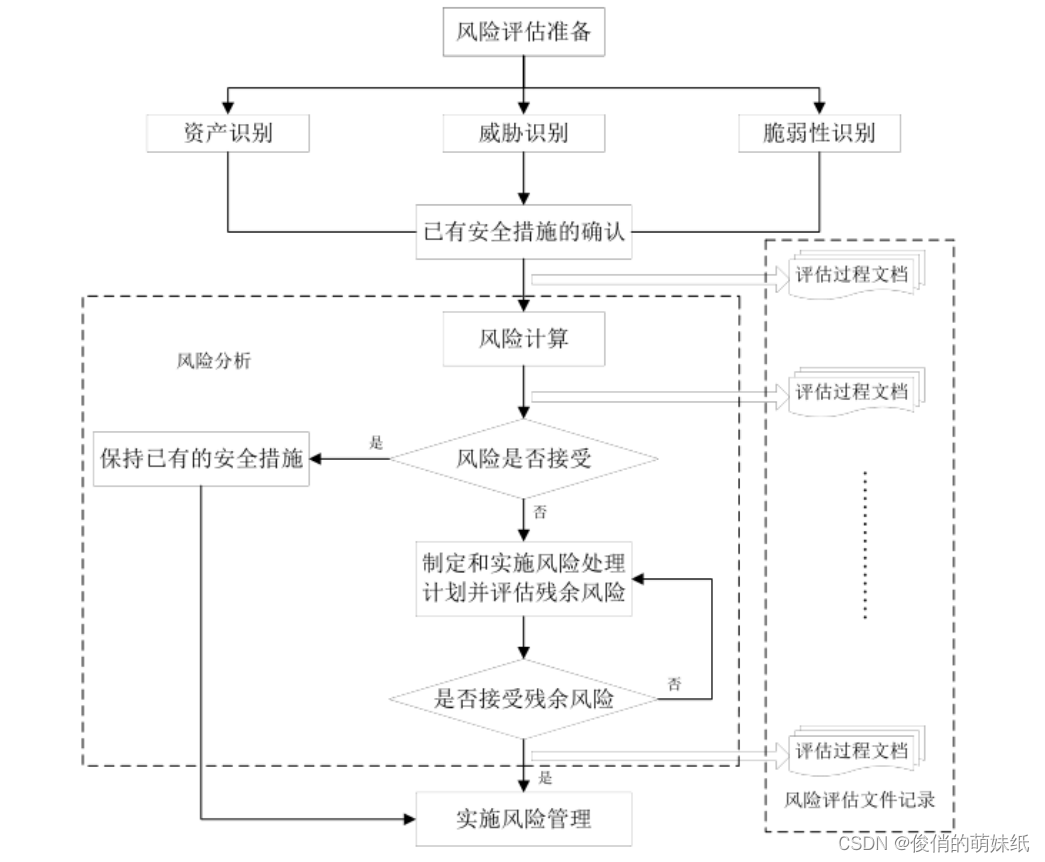
安全测试报告-模板内容
1. 概述 为检验XXXX平台 系统的安全性,于 XXXX年 XX 月 XX 日至 XXXX年 XX 月 XX日对目标系统进行了安全测试。在此期间测试人员将使用各 种非破坏性质的攻击手段,对目标系统做深入的探测分析,进而挖掘系统中的安 全漏洞和风险隐患。研发团队…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...
