使用Numpy手工模拟梯度下降算法
代码
import numpy as np # Compute every step manually# Linear regression
# f = w * x # here : f = 2 * x
X = np.array([1, 2, 3, 4], dtype=np.float32)
Y = np.array([2, 4, 6, 8], dtype=np.float32)w = 0.0# model output
def forward(x):return w * x# loss = MSE
def loss(y, y_pred):return ((y_pred - y)**2).mean()# J = MSE = 1/N * (w*x - y)**2
# dJ/dw = 1/N * 2x(w*x - y)
def gradient(x, y, y_pred):return np.mean(2*x*(y_pred - y))print(f'Prediction before training: f(5) = {forward(5):.3f}')# Training
learning_rate = 0.01
n_iters = 20for epoch in range(n_iters):# predict = forward passy_pred = forward(X)# lossl = loss(Y, y_pred)# calculate gradientsdw = gradient(X, Y, y_pred)# update weightsw -= learning_rate * dwif epoch % 2 == 0:print(f'epoch {epoch+1}: w = {w:.3f}, loss = {l:.8f}')print(f'Prediction after training: f(5) = {forward(5):.3f}')
输出
Prediction before training: f(5) = 0.000
epoch 1: w = 0.300, loss = 30.00000000
epoch 3: w = 0.772, loss = 15.66018677
epoch 5: w = 1.113, loss = 8.17471600
epoch 7: w = 1.359, loss = 4.26725292
epoch 9: w = 1.537, loss = 2.22753215
epoch 11: w = 1.665, loss = 1.16278565
epoch 13: w = 1.758, loss = 0.60698175
epoch 15: w = 1.825, loss = 0.31684822
epoch 17: w = 1.874, loss = 0.16539653
epoch 19: w = 1.909, loss = 0.08633806
Prediction after training: f(5) = 9.612
代码步骤详细解释
让我们通过一步一步地代入具体值来解释为什么在给定的线性回归示例中,权重 w w w 逐渐接近真实值,并且损失函数的值持续减小。这个过程展示了梯度下降法如何通过逐步迭代更新模型的权重 w w w 来最小化损失函数。
初始设置
- 真实函数为 f ( x ) = 2 x f(x) = 2x f(x)=2x,我们的目标是通过学习找到这个关系。
- 初始权重 w = 0.0 w = 0.0 w=0.0。
- 学习率 α = 0.01 \alpha = 0.01 α=0.01。
- 输入 X = [ 1 , 2 , 3 , 4 ] X = [1, 2, 3, 4] X=[1,2,3,4],对应的真实输出 Y = [ 2 , 4 , 6 , 8 ] Y = [2, 4, 6, 8] Y=[2,4,6,8]。
第一次迭代
-
前向传播:使用初始权重 w = 0.0 w = 0.0 w=0.0 进行预测,
y pred = w × X = 0 × X = [ 0 , 0 , 0 , 0 ] y_{\text{pred}} = w \times X = 0 \times X = [0, 0, 0, 0] ypred=w×X=0×X=[0,0,0,0] -
计算损失(MSE):损失函数为 J = MSE = 1 N ∑ ( y pred − Y ) 2 J=\text{MSE} = \frac{1}{N} \sum (y_{\text{pred}} - Y)^2 J=MSE=N1∑(ypred−Y)2,
MSE = 1 4 ( ( 0 − 2 ) 2 + ( 0 − 4 ) 2 + ( 0 − 6 ) 2 + ( 0 − 8 ) 2 ) = 30 \text{MSE} = \frac{1}{4} \left((0-2)^2 + (0-4)^2 + (0-6)^2 + (0-8)^2\right) = 30 MSE=41((0−2)2+(0−4)2+(0−6)2+(0−8)2)=30 -
计算梯度:梯度 d J d w = 1 N ∑ 2 x ( w × x − y ) \frac{dJ}{dw} = \frac{1}{N} \sum 2x (w \times x - y) dwdJ=N1∑2x(w×x−y),
d J d w = 1 4 ∑ 2 X ( 0 × X − Y ) = 1 4 ∑ 2 X ( − Y ) \frac{dJ}{dw} = \frac{1}{4} \sum 2X (0 \times X - Y) = \frac{1}{4} \sum 2X (-Y) dwdJ=41∑2X(0×X−Y)=41∑2X(−Y)
d J d w = 1 4 × 2 × ( ( 1 × − 2 ) + ( 2 × − 4 ) + ( 3 × − 6 ) + ( 4 × − 8 ) ) = − 30 \frac{dJ}{dw} = \frac{1}{4} \times 2 \times ((1 \times -2) + (2 \times -4) + (3 \times -6) + (4 \times -8)) = -30 dwdJ=41×2×((1×−2)+(2×−4)+(3×−6)+(4×−8))=−30 -
更新权重: w = w − α d J d w w = w - \alpha \frac{dJ}{dw} w=w−αdwdJ,
w = 0.0 − 0.01 × ( − 30 ) = 0.3 w = 0.0 - 0.01 \times (-30) = 0.3 w=0.0−0.01×(−30)=0.3
这个过程解释了第一次迭代后为什么 w w w 更新为 0.3 并且损失减少到 30。梯度 d J d w = − 30 \frac{dJ}{dw} = -30 dwdJ=−30 指示了 w w w 需要增加来减少损失。
推导梯度
对于给定的输入 X X X 和输出 Y Y Y,梯度的计算可以展开为:
d J d w = 1 N ∑ 2 x ( w × x − y ) \frac{dJ}{dw} = \frac{1}{N} \sum 2x (w \times x - y) dwdJ=N1∑2x(w×x−y)
代入第一次迭代的值,
d J d w = 1 4 × 2 × [ 1 × ( 0 × 1 − 2 ) + 2 × ( 0 × 2 − 4 ) + 3 × ( 0 × 3 − 6 ) + 4 × ( 0 × 4 − 8 ) ] \frac{dJ}{dw} = \frac{1}{4} \times 2 \times [1 \times (0 \times 1 - 2) + 2 \times (0 \times 2 - 4) + 3 \times (0 \times 3 - 6) + 4 \times (0 \times 4 - 8)] dwdJ=41×2×[1×(0×1−2)+2×(0×2−4)+3×(0×3−6)+4×(0×4−8)]
= 1 4 × 2 × [ − 2 − 8 − 18 − 32 ] = − 30 = \frac{1}{4} \times 2 \times [-2 -8 -18 -32] = -30 =41×2×[−2−8−18−32]=−30
让我们通过代入具体值来详细展示线性回归示例中第二次迭代的推导过程。
第二次迭代的起点
- 初始权重(从第一次迭代更新后): w = 0.3 w = 0.3 w=0.3
- 学习率: α = 0.01 \alpha = 0.01 α=0.01
- 输入: X = [ 1 , 2 , 3 , 4 ] X = [1, 2, 3, 4] X=[1,2,3,4]
- 真实输出: Y = [ 2 , 4 , 6 , 8 ] Y = [2, 4, 6, 8] Y=[2,4,6,8]
前向传播
计算预测值 y pred y_{\text{pred}} ypred:
y pred = w × X = 0.3 × [ 1 , 2 , 3 , 4 ] = [ 0.3 , 0.6 , 0.9 , 1.2 ] y_{\text{pred}} = w \times X = 0.3 \times [1, 2, 3, 4] = [0.3, 0.6, 0.9, 1.2] ypred=w×X=0.3×[1,2,3,4]=[0.3,0.6,0.9,1.2]
损失计算(MSE)
L = 1 N ∑ i = 1 N ( y pred , i − Y i ) 2 L = \frac{1}{N} \sum_{i=1}^{N} (y_{\text{pred}, i} - Y_i)^2 L=N1i=1∑N(ypred,i−Yi)2
L = 1 4 ( ( 0.3 − 2 ) 2 + ( 0.6 − 4 ) 2 + ( 0.9 − 6 ) 2 + ( 1.2 − 8 ) 2 ) L = \frac{1}{4} \left((0.3-2)^2 + (0.6-4)^2 + (0.9-6)^2 + (1.2-8)^2\right) L=41((0.3−2)2+(0.6−4)2+(0.9−6)2+(1.2−8)2)
L = 1 4 ( 2.89 + 11.56 + 26.01 + 46.24 ) L = \frac{1}{4} \left(2.89 + 11.56 + 26.01 + 46.24\right) L=41(2.89+11.56+26.01+46.24)
L = 1 4 × 86.7 = 21.675 L = \frac{1}{4} \times 86.7 = 21.675 L=41×86.7=21.675
梯度计算
d L d w = 1 N ∑ i = 1 N 2 x i ( w x i − Y i ) \frac{dL}{dw} = \frac{1}{N} \sum_{i=1}^{N} 2x_i (w x_i - Y_i) dwdL=N1i=1∑N2xi(wxi−Yi)
d L d w = 1 4 × 2 × [ 1 × ( 0.3 × 1 − 2 ) + 2 × ( 0.3 × 2 − 4 ) + 3 × ( 0.3 × 3 − 6 ) + 4 × ( 0.3 × 4 − 8 ) ] \frac{dL}{dw} = \frac{1}{4} \times 2 \times [1 \times (0.3 \times 1 - 2) + 2 \times (0.3 \times 2 - 4) + 3 \times (0.3 \times 3 - 6) + 4 \times (0.3 \times 4 - 8)] dwdL=41×2×[1×(0.3×1−2)+2×(0.3×2−4)+3×(0.3×3−6)+4×(0.3×4−8)]
d L d w = 1 4 × 2 × [ ( − 1.7 ) + ( − 7.4 ) + ( − 16.1 ) + ( − 28.8 ) ] \frac{dL}{dw} = \frac{1}{4} \times 2 \times [(-1.7) + (-7.4) + (-16.1) + (-28.8)] dwdL=41×2×[(−1.7)+(−7.4)+(−16.1)+(−28.8)]
d L d w = 1 4 × 2 × [ − 53.999 ] = − 27.0 \frac{dL}{dw} = \frac{1}{4} \times 2 \times [-53.999] = -27.0 dwdL=41×2×[−53.999]=−27.0
更新权重
使用梯度下降法更新 w w w:
w = w − α × d L d w w = w - \alpha \times \frac{dL}{dw} w=w−α×dwdL
w = 0.3 − 0.01 × ( − 25.5 ) = 0.3 + 0.255 = 0.555 w = 0.3 - 0.01 \times (-25.5) = 0.3 + 0.255 = 0.555 w=0.3−0.01×(−25.5)=0.3+0.255=0.555
这一系列计算表明,在第二次迭代中,通过计算损失和梯度,并根据这个梯度更新权重,权重 w w w 从 0.3 更新到了 0.555。这一过程逐步将模型从初步猜测调整为更接近真实模型 f ( x ) = 2 x f(x) = 2x f(x)=2x 的参数,损失从 21.675 21.675 21.675 减少,显示了模型准确度的提高。
总结
通过不断重复这个过程(前向传播、损失计算、梯度计算、权重更新), w w w 逐步被调整,以最小化模型的总损失。每次迭代,梯度告诉我们如何调整 w w w 以减少损失,学习率 α \alpha α 控制了这个调整的步长。随着迭代的进行,模型预测 y pred y_{\text{pred}} ypred 会逐渐接近真实值 Y Y Y,损失函数值会持续减小,直至收敛到最小值或达到学习的终止条件。
为什么梯度方向表明了减少损失的方向?
第一轮迭代中,梯度 d J d w = − 30 \frac{dJ}{dw} = -30 dwdJ=−30 指出了权重 w w w 需要增加以减少损失。这是因为在梯度下降法中,我们通过从当前权重中减去梯度乘以学习率(一个小的正数)来更新权重。如果梯度为负(如此例中的 − 30 -30 −30),减去一个负数相当于向正方向(增加)调整权重。
在梯度下降法中,梯度 d J d w \frac{dJ}{dw} dwdJ 描述了损失函数 J J J 关于权重 w w w 的变化率。如果梯度为负,这意味着增加 w w w 可以减少损失 J J J;如果梯度为正,减少 w w w 可以减少损失。
具体来说:
- 梯度为负( d J d w < 0 \frac{dJ}{dw} < 0 dwdJ<0):这意味着增加权重 w w w (向梯度的反方向移动)会导致损失 J J J 减小。因此,为了减少损失,我们需要增加 w w w。
- 权重更新公式( w = w − α d J d w w = w - \alpha \frac{dJ}{dw} w=w−αdwdJ)中,当 d J d w \frac{dJ}{dw} dwdJ 为负时, w w w 的更新实际上会增加 w w w 的值。
在我们的例子中,通过这种方式更新 w w w(从 0.0 0.0 0.0 更新到 0.3 0.3 0.3),正是因为我们沿着减少损失的方向调整了 w w w,使得模型的预测与真实值之间的差异减小了,进而损失函数值减少。这个过程在多次迭代后,逐渐使模型更加准确,最终找到一个能够最小化损失函数的 w w w 值。
相关文章:

使用Numpy手工模拟梯度下降算法
代码 import numpy as np # Compute every step manually# Linear regression # f w * x # here : f 2 * x X np.array([1, 2, 3, 4], dtypenp.float32) Y np.array([2, 4, 6, 8], dtypenp.float32)w 0.0# model output def forward(x):return w * x# loss MSE def loss…...
金融数据采集与风险管理:Open-Spider工具的应用与实践
一、项目介绍 在当今快速发展的金融行业中,新的金融产品和服务层出不穷,为银行业务带来了巨大的机遇和挑战。为了帮助银行员工更好地应对这些挑战,我们曾成功实施了一个创新的项目,该项目采用了先进的爬虫技术,通过ope…...

鸿蒙Harmony应用开发—ArkTS声明式开发(通用属性:动态属性设置)
动态设置组件的属性,支持开发者在属性设置时使用if/else语法,且根据需要使用多态样式设置属性。 说明: 从API Version 11开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 attributeModifier attributeMo…...

Vue class和style绑定:动态美化你的组件
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

[C++] Windows中字符串函数的种类
文章目录 C标准库函数VC CRT函数Win32 APILinux C标准库函数 #include || #include <string.h> || #include 都可以使用以下函数: char *strcpy(char *dest, const char *src) //将Src字符串拷贝到Dst字符串地址。没有目标内存大小检查,可能会导致…...
Django工具
一、分页器介绍 1.1、介绍 分页,就是当我们在页面中显示一些信息列表,内容过多,一个页面显示不完,需要分成多个页面进行显示时,使用的技术就是分页技术 在django项目中,一般是使用3种分页的技术: 自定义分页功能,所有的分页功能都是自己实现django的插件 django-pagin…...
vue ui Starting GUI 图形化配置web新项目
前言:在vue框架里面, 以往大家都是习惯用命令行 vue create 、vue init webpack创建新前端项目,而vue ui是一个可视化的图形界面,对于新手来说更加友好了,不但可以创建、管理、还可以更新vue项目,也可以下载…...

Unity InputField宽度自适应内容
在Unity中,InputField在我们输入内容时,只会显示适应初始宽度的最新内容,或者自定义长度内容。 那么,要实现宽度自适应内容就需要另寻他法了。 以下是通过一个控制脚本来实现的一个简单方法。 直接上脚本: using S…...
加快代码审查的 7 个最佳实践
目录 前言 1-保持小的拉取请求 2-使用拉取请求模板 3-实施响应时间 SLA 4-培训初级和中级工程师 5-设置持续集成管道 6-使用拉取请求审查应用程序 7-生成图表以可视化您的代码更改 前言 代码审查可能会很痛苦软件工程师经常抱怨审查过程缓慢,延迟下游任务&…...
)
C++读写Excel(xlnt库的使用)
一、简介 官网:https://github.com/tfussell/xlnt Cross-platform user-friendly xlsx library for C11 xlnt is a modern C library for manipulating spreadsheets in memory and reading/writing them from/to XLSX files as described in ECMA 376 4th edition…...

【工具】conda常用命令
Conda 是一个流行的包管理器和环境管理器,用于安装、部署和管理软件包及其依赖项。 创建环境: conda create --name myenv 这将创建一个名为 myenv 的新环境。 激活环境: conda activate myenv 这会激活名为 myenv 的环境。在 Windows 上&am…...

Dockerfile编写实践篇
Docker通过一种打包和分发的软件,完成传统容器的封装。这个用来充当容器分发角色的组件被称为镜像。Docker镜像是一个容器中运行程序的所有文件的捆绑快照。当使用Docker分发软件,其实就是分发这些镜像,并在接收的机器上创建容器。镜像在Dock…...

BJFU|计算机网络缩写对照表
之前有过这个题型,但23年没考,所以按需准备 A ACK (ACKnowledgement) 确认 ADSL (Asymmetric Digital Subscriber Line) 非对称数字用户线 API (Applicatin Programming Interface) 应用编程接口 ARP (Address Resolution Protocol) 地址解析协议 ARQ (…...
Grafana dashboards as ConfigMaps
文章目录 1. 简介2. 创建 configmaps3. grafana 界面查看 1. 简介 将 Grafana 仪表板存储为 Kubernetes ConfigMap 相比传统的通过 Grafana 界面导入仪表板有以下一些主要优点: 版本控制: ConfigMap 可以存储在版本控制系统(如Git)中,便于跟踪和管理仪表板的变更历…...

【QA-SYSTEMS】CANTATA-解决Jenkins中build Cantata报错
【更多软件使用问题请点击亿道电子官方网站查询】 1、 文档目标 解决Jenkins中build Cantata测试项目报找不到license server的错误。 2、 问题场景 在Jenkins中build Cantata测试项目,报错“Failed to figure out the license server correctly”。 3、软硬件环…...

个人网站展示(静态)
大学期间做了一个个人博客网站,纯H5编码的网站,利用php搭建了一个留言模块。 有需要源码的同学,可以联系我~ 首页: IT杂记模块 文人墨客模块 劳有所获模块 生活日志模块 关于我 一个推崇全栈开发的前端开发人员 微信: itrzzh …...

C++——内存管理、模板
一、C内存管理 在C语言中我们曾学习过动态内存管理的相关知识,通过malloc、calloc、realloc和free等对堆上的空间进行申请和释放。在C中我们同样会面临类似的需求,因此C对动态开辟内存的方式进行了一些调整,我们可以使用new和delete操作符来对…...

商品上传上货搬家使用1688商品采集api接口
1688.item_get 公共参数 名称类型必须描述keyString是调用key(必须以GET方式拼接在URL中)secretString是调用密钥api_nameString是API接口名称(包括在请求地址中)[item_search,item_get,item_search_shop等]cacheString否[yes,no…...
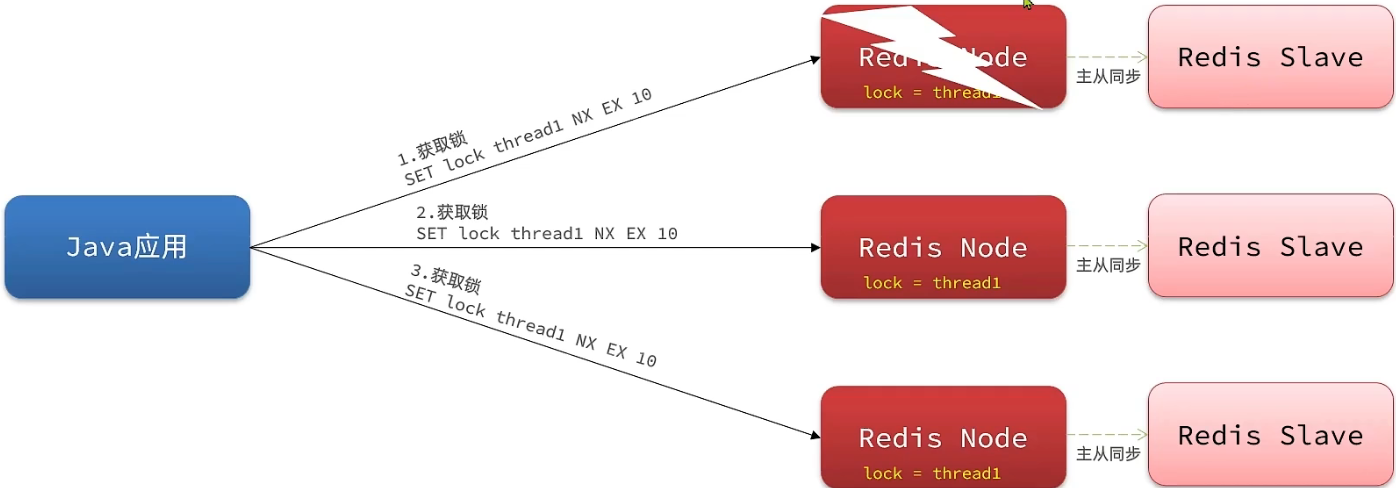
redisson解决redis服务器的主从一致性问题
redisson解决redis的主节点和从节点一致性的问题。从而解决锁被错误获取的情况。 实际开发中我们会搭建多台redis服务器,但这些服务器分主次,主服务器负责处理写的操作(增删改),从服务器负责处理读的操作,…...

Vue-router
router的使用(52) 5个基础步骤: 1.在终端执行yarn add vue-router3.6.5,安装router插件 yarn add vue-router3.6.5 2.在文件的main.js中引入router插件 import VueRouter from vue-router 3.在main.js中安装注册Vue.use(Vue…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
