备考2025年AMC8数学竞赛:吃透2000-2024年600道AMC8真题就够
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的孩子来说,吃透AMC8历年真题是备考最科学、最有效的方法之一。
即使不参加AMC8竞赛,吃透了历年真题600道和背后的知识体系,那么小学和初中数学一定会学得非常轻松、游刃有余。(当然,我个人建议孩子有余力的情况下还是参加,以赛促学是一种很不错的做法,能够激发孩子的好胜心和学习热情,也是孩子宝贵的经历、体验。)

为帮助孩子们更高效地备考,我整理了2000-2004年的全部AMC8真题(完整版共600道,且修正了原试卷中的少量bug),并且独家制作了多种在线练习,利用碎片化时间,一年足以通过自学在2025年AMC8竞赛中取得好成绩。详情见文末。
2000-2024年AMC8真题和解析:2017年第19题

这道题的考点是数论(整除)。
对表达式进行调整,得到:98!+99!+100!=98(1+99+9900)=98!*10000=98!*2^4*5^4。所以根据题意,要求表达式的因子,只需要确定98!里有多少个5即可。直接应用下列公式可得98!里面最多有22个5,所以最终一共有22+4=26个5,答案为D。

2000-2024年AMC8真题和解析:2016年第9题

这道题的考点是数论(质因数分解)。
2016的质因数分解为2016=2^5×3^2×7,所以它的不同质因数为2,3和7,和为12,答案选B。
2000-2024年AMC8真题和解析:2013年第13题

这道题的考点是代数。
我们假设Clara实际总分的十位为a,个位为b,则这个分数本来应该是10a+b。但是Clara调换了十位和个位的位置,变成了10b十a,那么正确总分和不正确总分的差为9a-9b,分解因式结果为|9(a一b)|,表明这个差应该是9的倍数。选项中为9的倍数的只有45,所以答案选A。
提醒:这种题型也经常出现,将各个尾数上的数字假设后列出表达式是常用的解题思路。
2000-2024年AMC8真题和解析:2007年第9题

这道题的考点是逻辑推理,类似于一个简单的数独。
- 我们看先第1行,第4列的数字一定是3,因为若3在第1行第2列,那么第2列将有两个3。
- 同样的分析,第2行第4列一定是1。
- 那么第4列右下角的数字只能是2,所以答案选B。
2000-2024年AMC8真题和解析:2003年第21题

这道题的考点是平面几何(勾股定理)。
在原图中,作如下两根辅助线:
由梯形的面积公式,我们有164=8*(BC+AD)/2。因此BC+AD=41。
过B和C作BE⊥AD,CF⊥AD,则BE=CF=8。在直角△ABE和直角△CFD中分别运用勾股定理,得到AE=6,DF=15。那么则AD=BC+21。代入梯形ABCD的面积公式得到:BC+AD=41,即BC+BC+21=41,解得,BC=10,答案选B。
提醒:AMC8中的平面几何题目通常难度不算太高,辅助线添加正确了基本上就能做对。
六分成长针对AMC8备考资源,欢迎了解更多
上述六分成长独家制作的在线练习题,符合学习和认知心理学,来源于完整的历年AMC8真题,并且会持续更新。AMC8备考可用,反复练习,也有利于小学、初中数学能力提升。
还有配套的系统学习文档、视频资料赠送。欢迎了解。

相关文章:

备考2025年AMC8数学竞赛:吃透2000-2024年600道AMC8真题就够
我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的孩子来说,吃透AMC8历年真题是备考最科学、最有效的方法之一。 即使不参加AMC8竞赛,吃透了历年真题600道和背后的知识体系,那么…...
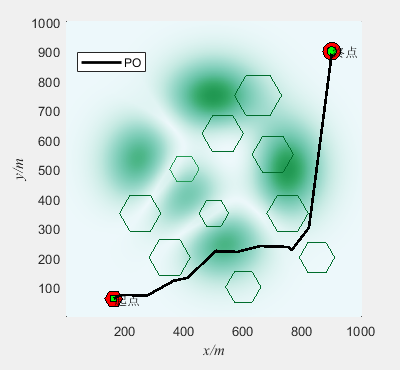
基于鹦鹉优化算法(Parrot optimizer,PO)的无人机三维路径规划(提供MATLAB代码)
一、无人机路径规划模型介绍 无人机三维路径规划是指在三维空间中为无人机规划一条合理的飞行路径,使其能够安全、高效地完成任务。路径规划是无人机自主飞行的关键技术之一,它可以通过算法和模型来确定无人机的航迹,以避开障碍物、优化飞行…...

linux Shell 命令行-02-var 变量
拓展阅读 linux Shell 命令行-00-intro 入门介绍 linux Shell 命令行-02-var 变量 linux Shell 命令行-03-array 数组 linux Shell 命令行-04-operator 操作符 linux Shell 命令行-05-test 验证是否符合条件 linux Shell 命令行-06-flow control 流程控制 linux Shell 命…...

C#MQTT编程10--MQTT项目应用--工业数据上云
1、文章回顾 这个系列文章已经完成了9个内容,由浅入深地分析了MQTT协议的报文结构,并且通过一个有效的案例让伙伴们完全理解理论并应用到实际项目中,这节继续上马一个项目应用,作为本系列的结束,奉献给伙伴们&#x…...

exceljs解析和生成excel文件
安装 npm install exceljs解析excel 通过 Workbook 的 readFile 方法可以拿到workbook对象, workbook对象包含的概念有 worksheet(工作表) --> row(行) --> cell(单元格).于是可以通过依次遍历 worksheet, row, cell来拿到单元格的数据直接通过 worksheet.getSheetValue…...
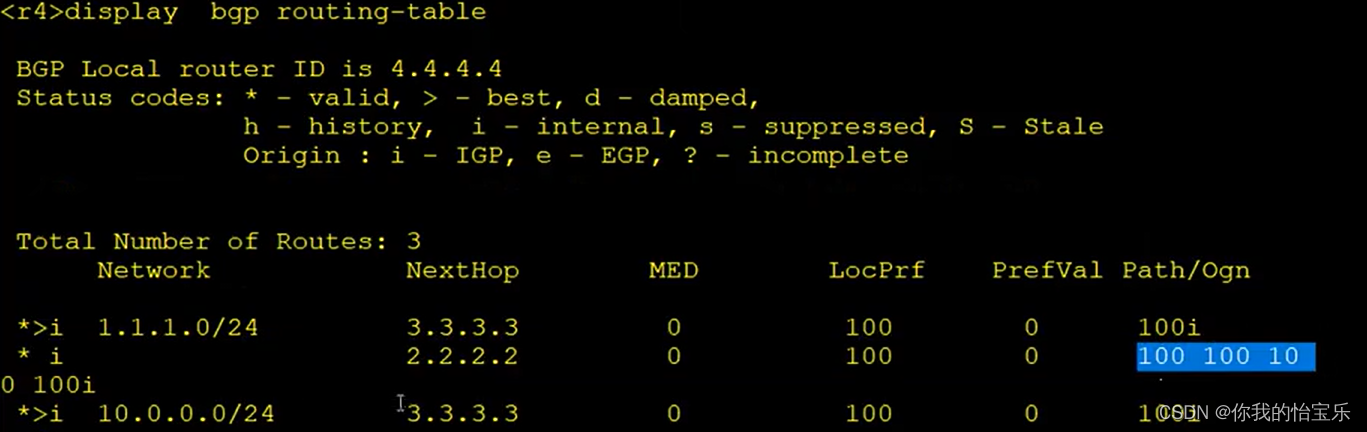
HCIP —— BGP 路径属性 (上)
目录 BGP 路径属性 1.优选Preferred-Value属性值最大的路由 2.优选Local-preference 属性数值大的路由 3.本地始发的BGP路由优先于其他对等体处学习到的路由。 4..优选AS_PATH属性值最短的路由 BGP 路径属性 BGP的路由选路是存在优选规则的,下图为华为官网提供…...
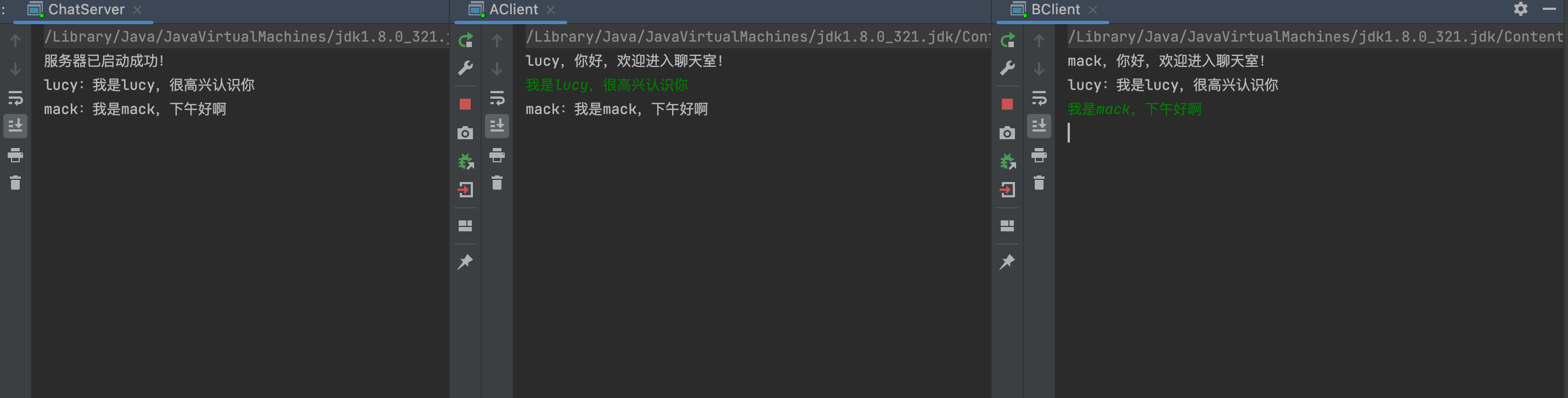
NIO学习总结(二)——Selector、FileLock、Path、Files、聊天室实现
一、Selector 1.1 Selector简介 1.1.1 Selector 和 Channel的关系 Selector 一般称为选择器 ,也可以翻译为 多路复用器 。 它是 Java NIO 核心组件中的一个,用于检查一个或多个 NIO Channel(通道)的状态是否处于可读、可写。由…...
)
面试经典150题(111-113)
leetcode 150道题 计划花两个月时候刷完之未完成后转,今天(第5天)完成了3道(111-113)150 111.(172. 阶乘后的零)题目描述: 给定一个整数 n ,返回 n! 结果中尾随零的数量。 提示 n! n * (n - 1…...
iOS17.4获取UDID安装mobileconfig描述文件失败 提示“安全延迟进行中”问题 | 失窃设备保护
iOS17.4这两天已经正式发布, 在iOS 17.4版本中新增了一个名为"失窃设备保护"的功能,并提供了一个"需要安全延迟"的选项。 iOS17.4获取UDID安装mobileconfig描述文件失败 提示“安全延迟进行中”问题 | 失窃设备保护 当用户选择启用…...

List--splice使用技巧
splice : 拼接两个list api: void dump(list<int>& li) {for(auto & i :li)cout<<i<< " ";cout<<endl; } int main() { list<int> li1 {1,3,5};list<int> li2 {2,4,6}; }1 c.splice(pos,c2); // li的开头插入li2链表…...

【最新版】ChatGPT/GPT4科研应用与AI绘图论文写作(最新增加Claude3、Gemini、Sora、GPTs技术及AI领域中的集中大模型的最新技术)
2023年随着OpenAI开发者大会的召开,最重磅更新当属GPTs,多模态API,未来自定义专属的GPT。微软创始人比尔盖茨称ChatGPT的出现有着重大历史意义,不亚于互联网和个人电脑的问世。360创始人周鸿祎认为未来各行各业如果不能搭上这班车…...
离线数仓(六)【ODS 层开发】
前言 1、ODS 层开发 ODS层的设计要点如下: (1)ODS层的表结构设计依托于从业务系统同步过来的数据结构(JSON/CSV/TSV)。 (2)ODS层要保存全部历史数据,故其压缩格式应选择高压缩比的…...

PPT只要出现弹窗就闪退,Word和Excel都是正常的
1. 问题描述 PPT在常规使用下,能进行正常编辑和保存,但在使用过程中出现弹窗,类似于报错或者打开文件选项就会出现闪退,或者在添加新建页时选用右键添加时也会出现闪退。 找了很久的办法,才得到解决。记录一下。 2.…...

21、电源管理入门之芯片设计中的电源管理
目录 1. 关于PCSA和SCP 2. 关于PSCI和SCMI 3. 关于芯片SoC设计中的一些要点 参考: 这里以ARM为例来进行说明,我们在做驱动软件的时候,就需要跟硬件SoC里面的IP打交道,通过操作寄存器来实现硬件功能。之前的文章:ARM SCP入门-AP与SCP通信中3和4章节已经进行了简单介绍,…...

电脑打字突然变成繁体字如何修改
1. 右键电脑右下角的“中”字 2. 点击字符集,选中简体即可 有用的话记得给我点个赞啊~ 靴靴!...
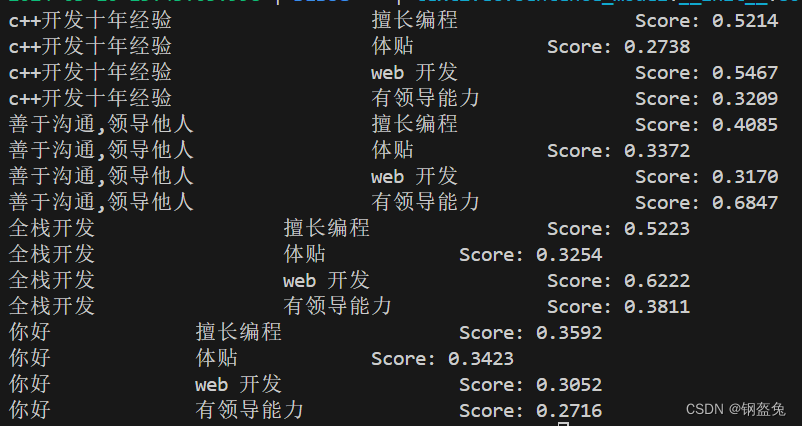
NLP:文本相似度计算
前面我们已经实现了把长段的句子,利用HanLP拆分成足够精炼的分词,后面我们要实现“联想”功能,我这里初步只能想到通过文本相似度计算来实现。下面介绍一下文本相似度计算 (当然HanLP也有文本相似度计算的方法,这里我…...

复合查询【MySQL】
文章目录 复合查询测试表 单表查询多表查询子查询单行子查询多行子查询IN 关键字ALL 关键字ANY 关键字 多列子查询 合并查询 复合查询 测试表 雇员信息表中包含三张表,分别是员工表(emp)、部门表(dept)和工资等级表&…...

【Pytorch】进阶学习:深入解析 sklearn.metrics 中的 classification_report 函数---分类性能评估的利器
【Pytorch】进阶学习:深入解析 sklearn.metrics 中的 classification_report 函数—分类性能评估的利器 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合…...
探索云原生数据库技术:构建高效可靠的云原生应用
数据库是应用开发中非常重要的组成部分,可以进行数据的存储和管理。随着企业业务向数字化、在线化和智能化的演进过程中,面对指数级递增的海量存储需求和挑战以及业务带来的更多的热点事件、突发流量的挑战,传统的数据库已经很难满足和响应快…...
Jmeter+Ant+Git/SVN+Jenkins实现持续集成接口测试,一文精通(一)
前言 Jmeter,Postman一些基本大家相比都懂。那么真实在项目中去使用,又是如何使用的呢?本文将一文详解jmeter接口测试 一、接口测试分类 二、目前接口架构设计 三、市面上的接口测试工具 四、Jmeter简介,安装,环境…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
