矩阵求导笔记
文章目录
- 1. ML中为什么需要矩阵求导
- 2. 向量函数与矩阵求导初印象
- 3. YX 拉伸术
- 3.1 f(x)为标量,X为列向量
- 3.2 f(x)为列向量,X 为标量
- 3.3 f(x)为列向量,X 为列向量
- 4. 常见矩阵求导公式
1. ML中为什么需要矩阵求导
-
简洁
用方程式表示如下:
y 1 = w 1 X 11 + w 2 X 12 (1) y_1=w_1X_{11}+w_2X_{12}\tag{1} y1=w1X11+w2X12(1)
y 2 = w 1 X 21 + w 2 X 22 (2) y_2=w_1X_{21}+w_2X_{22}\tag{2} y2=w1X21+w2X22(2)
转换成矩阵表示如下:
Y = X W (3) Y=XW\tag{3} Y=XW(3)
Y = [ y 1 y 2 ] , X = [ x 11 x 12 x 21 x 22 ] , W = [ w 1 w 2 ] (4) Y=\begin{bmatrix}y_1\\\\y_2\end{bmatrix},X=\begin{bmatrix}x_{11}&&x_{12}\\\\x_{21}&&x_{22}\end{bmatrix},W=\begin{bmatrix}w_{1}\\\\w_{2}\end{bmatrix}\tag{4} Y= y1y2 ,X= x11x21x12x22 ,W= w1w2 (4) -
快速
当使用python 中的numpy 库时候,在相对于 for 循环,Numpy 本身的计算提速相当快 -
源代码
import time
import numpy as npif __name__ == "__main__":N = 1000000a = np.random.rand(N)b = np.random.rand(N)start = time.time()c = np.dot(a,b)stop = time.time()print(f"c={c}")print("vectorized version: " + str(1000*(stop-start))+"ms")c = 0start1 = time.time()for i in range(N):c += a[i]*b[i]stop1 = time.time()print(f"c={c}")print("for loop: " + str(1000*(stop1-start1))+"ms")times1 = (stop1-start1)/(stop-start)print(f"times1={times1}")
- 结果
c=250071.8870070607
vectorized version: 6.549358367919922ms
c=250071.88700706122
for loop: 265.43641090393066ms
times1=40.52861303239898# 向量化居然比单独的for循环快40倍
2. 向量函数与矩阵求导初印象
- 标量函数:输出为标量的函数
f ( x ) = x 2 ⇒ x ∈ R → x 2 ∈ R f(x)=x^2\Rightarrow x\in R\rightarrow x^2 \in R f(x)=x2⇒x∈R→x2∈R
f ( x ) = x 1 2 + x 2 2 ⇒ [ x 1 x 2 ] ∈ R 2 → x 1 2 + x 2 2 ∈ R f(x)=x_1^2+x_2^2\Rightarrow \begin{bmatrix}x_1\\\\x_2\end{bmatrix}\in R^2\rightarrow x_1^2+x_2^2 \in R f(x)=x12+x22⇒ x1x2 ∈R2→x12+x22∈R - 向量函数:输出为向量或矩阵的函数
<1> 输入标量,输出向量
f ( x ) = [ f 1 ( x ) = x f 2 ( x ) = x 2 ] ⇒ x ∈ R , [ x x 2 ] ∈ R 2 f(x)=\begin{bmatrix}f_1(x)=x\\\\f_2(x)=x^2\end{bmatrix}\Rightarrow x\in R,\begin{bmatrix}x\\\\x^2\end{bmatrix} \in R^2 f(x)= f1(x)=xf2(x)=x2 ⇒x∈R, xx2 ∈R2
<2> 输入标量,输出矩阵
f ( x ) = [ f 11 ( x ) = x f 12 ( x ) = x 2 f 21 ( x ) = x 3 f 22 ( x ) = x 4 ] ⇒ x ∈ R , [ x x 2 x 3 x 4 ] ∈ R 2 × 2 f(x)=\begin{bmatrix}f_{11}(x)=x&&f_{12}(x)=x^2\\\\f_{21}(x)=x^3&&f_{22}(x)=x^4\end{bmatrix}\Rightarrow x\in R,\begin{bmatrix}x&&x^2\\\\x^3&&x^4\end{bmatrix} \in R^{2\times2} f(x)= f11(x)=xf21(x)=x3f12(x)=x2f22(x)=x4 ⇒x∈R, xx3x2x4 ∈R2×2
<3> 输入向量,输出矩阵
f ( x ) = [ f 11 ( x ) = x 1 + x 2 f 12 ( x ) = x 1 2 + x 2 2 f 21 ( x ) = x 1 3 + x 2 3 f 22 ( x ) = x 1 4 + x 2 4 ] ⇒ [ x 1 x 2 ] ∈ R 2 , [ x 1 + x 2 x 1 2 + x 2 2 x 1 3 + x 2 3 x 1 4 + x 2 4 ] ∈ R 2 × 2 f(x)=\begin{bmatrix}f_{11}(x)=x_1+x_2&&f_{12}(x)=x_1^2+x_2^2\\\\f_{21}(x)=x_1^3+x_2^3&&f_{22}(x)=x_1^4+x_2^4\end{bmatrix}\Rightarrow \begin{bmatrix}x_1\\\\x_2\end{bmatrix} \in R^2,\begin{bmatrix}x_1+x_2&&x_1^2+x_2^2\\\\x_1^3+x_2^3&&x_1^4+x_2^4\end{bmatrix} \in R^{2\times2} f(x)= f11(x)=x1+x2f21(x)=x13+x23f12(x)=x12+x22f22(x)=x14+x24 ⇒ x1x2 ∈R2, x1+x2x13+x23x12+x22x14+x24 ∈R2×2 - 总结
矩阵求导的本质
d A d B = 矩阵 A 中的每个元素对矩阵 B 中的每个元素求导 \frac{\mathrm{d}A}{\mathrm{d}B}=矩阵A中的每个元素对矩阵B中的每个元素求导 dBdA=矩阵A中的每个元素对矩阵B中的每个元素求导
3. YX 拉伸术
3.1 f(x)为标量,X为列向量
- 标量不变,向量拉伸
- YX中,Y前面横向拉,X后面纵向拉
d f ( x ) d x , Y = f ( x ) 为标量, X = [ x 1 x 2 ⋮ x n ] 为列向量 \frac{\mathrm{d}f(x)}{\mathrm{d}x},Y=f(x)为标量,X=\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix}为列向量 dxdf(x),Y=f(x)为标量,X= x1x2⋮xn 为列向量
f ( x ) = f ( x 1 , x 2 , . . . . , x n ) 为标量 f(x)=f(x_1,x_2,....,x_n)为标量 f(x)=f(x1,x2,....,xn)为标量 - 标量 f ( x ) f(x) f(x)不变,向量X 因为在YX拉伸术中在Y后面,所以向量X纵向拉伸,实际上就是将多元函数的偏导写在一个列向量中
d f ( x ) d x = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\\\\frac{\partial f(x)}{\partial x_2}\\\\\vdots\\\\\frac{\partial f(x)}{\partial x_n}\end{bmatrix} dxdf(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)
3.2 f(x)为列向量,X 为标量
f ( x ) = [ f 1 ( x ) f 2 ( x ) ⋮ f n ( x ) ] ; X 为标量 f(x)=\begin{bmatrix}f_1(x)\\\\f_2(x)\\\\\vdots\\\\f_n(x)\end{bmatrix};X 为标量 f(x)= f1(x)f2(x)⋮fn(x) ;X为标量
- 标量不变,向量拉伸
- YX中,Y前面横向拉,X后面纵向拉
d f ( x ) d x = [ ∂ f 1 ( x ) ∂ x ∂ f 2 ( x ) ∂ x … ∂ f n ( x ) ∂ x ] \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\begin{bmatrix}\frac{\partial f_1(x)}{\partial x}&&\frac{\partial f_2(x)}{\partial x}&&\dots&&\frac{\partial f_n(x)}{\partial x}\end{bmatrix} dxdf(x)=[∂x∂f1(x)∂x∂f2(x)…∂x∂fn(x)]
3.3 f(x)为列向量,X 为列向量
f ( x ) = [ f 1 ( x ) f 2 ( x ) ⋮ f n ( x ) ] ; X = [ x 1 x 2 ⋮ x n ] 为列向量 f(x)=\begin{bmatrix}f_1(x)\\\\f_2(x)\\\\\vdots\\\\f_n(x)\end{bmatrix};X=\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix}为列向量 f(x)= f1(x)f2(x)⋮fn(x) ;X= x1x2⋮xn 为列向量
- 第一步先固定Y ,将 X 纵向拉
d f ( x ) d x = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\\\\frac{\partial f(x)}{\partial x_2}\\\\\vdots\\\\\frac{\partial f(x)}{\partial x_n}\end{bmatrix} dxdf(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x) - 第二步,看每一个项 ∂ f ( x ) ∂ x 1 \frac{\partial f(x)}{\partial x_1} ∂x1∂f(x),其中f(x)为列向量, x 1 x_1 x1为标量,那么可以看出要进行 Y 横向拉
∂ f ( x ) ∂ x 1 = [ ∂ f 1 ( x ) ∂ x 1 ∂ f 2 ( x ) ∂ x 1 … ∂ f n ( x ) ∂ x 1 ] \frac{\partial f(x)}{\partial x_1}=\begin{bmatrix}\frac{\partial f_1(x)}{\partial x_1}&&\frac{\partial f_2(x)}{\partial x_1}&&\dots&&\frac{\partial f_n(x)}{\partial x_1}\end{bmatrix} ∂x1∂f(x)=[∂x1∂f1(x)∂x1∂f2(x)…∂x1∂fn(x)] - 第三步 ,将每项整合如下
d f ( x ) d x = [ ∂ f 1 ( x ) ∂ x 1 ∂ f 2 ( x ) ∂ x 1 … ∂ f n ( x ) ∂ x 1 ∂ f 1 ( x ) ∂ x 2 ∂ f 2 ( x ) ∂ x 2 … ∂ f n ( x ) ∂ x 2 ⋮ ⋮ … ⋮ ∂ f 1 ( x ) ∂ x n ∂ f 2 ( x ) ∂ x n … ∂ f n ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\begin{bmatrix}\frac{\partial f_1(x)}{\partial x_1}&&\frac{\partial f_2(x)}{\partial x_1}&&\dots&&\frac{\partial f_n(x)}{\partial x_1}\\\\\frac{\partial f_1(x)}{\partial x_2}&&\frac{\partial f_2(x)}{\partial x_2}&&\dots&&\frac{\partial f_n(x)}{\partial x_2}\\\\\vdots&&\vdots&&\dots&&\vdots\\\\\frac{\partial f_1(x)}{\partial x_n}&&\frac{\partial f_2(x)}{\partial x_n}&&\dots&&\frac{\partial f_n(x)}{\partial x_n}\end{bmatrix} dxdf(x)= ∂x1∂f1(x)∂x2∂f1(x)⋮∂xn∂f1(x)∂x1∂f2(x)∂x2∂f2(x)⋮∂xn∂f2(x)…………∂x1∂fn(x)∂x2∂fn(x)⋮∂xn∂fn(x)
4. 常见矩阵求导公式
4.1 Y = A T X Y=A^TX Y=ATX
f ( x ) = A T X ; A = [ a 1 , a 2 , … , a n ] T ; X = [ x 1 , x 2 , … , x n ] T , 求 d f ( x ) d X f(x)=A^TX;\quad A=[a_1,a_2,\dots,a_n]^T;\quad X=[x_1,x_2,\dots,x_n]^T,求\frac{\mathrm{d}f(x)}{\mathrm{d}X} f(x)=ATX;A=[a1,a2,…,an]T;X=[x1,x2,…,xn]T,求dXdf(x)
- 由于 A T = 1 × n , X = n × 1 , 那么 f ( x ) 为标量,即表示数值 A^T=1\times n,X=n\times1,那么f(x)为标量,即表示数值 AT=1×n,X=n×1,那么f(x)为标量,即表示数值,
- 标量不变,向量拉伸
- YX中,Y前面横向拉,X后面纵向拉
f ( x ) = ∑ i = 1 N a i x i f(x)=\sum_{i=1}^Na_ix_i f(x)=i=1∑Naixi
d f ( x ) d X = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\\\\frac{\partial f(x)}{\partial x_2}\\\\\vdots\\\\\frac{\partial f(x)}{\partial x_n}\end{bmatrix} dXdf(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x) - 可以计算 ∂ f ( x ) ∂ x i \frac{\partial f(x)}{\partial x_i} ∂xi∂f(x)
∂ f ( x ) ∂ x i = a i \frac{\partial f(x)}{\partial x_i}=a_i ∂xi∂f(x)=ai - 可得如下:
d f ( x ) d X = [ a 1 a 2 ⋮ a n ] = A \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}a_1\\\\a_2\\\\\vdots\\\\a_n\end{bmatrix}=A dXdf(x)= a1a2⋮an =A - 结论:
当 f ( x ) = A T X 当f(x)=A^TX 当f(x)=ATX
d f ( x ) d X = A \frac{\mathrm{d}f(x)}{\mathrm{d}X}=A dXdf(x)=A
4.2 Y = X T A X Y=X^TAX Y=XTAX
f ( x ) = X T A X ; A = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ … ⋮ a n 1 a n 2 … a n n ] ; X = [ x 1 , x 2 , … , x n ] T , 求 d f ( x ) d X f(x)=X^TAX;\quad A=\begin{bmatrix}a_{11}&&a_{12}&&\dots&&a_{1n}\\\\a_{21}&&a_{22}&&\dots&&a_{2n}\\\\\vdots&&\vdots&&\dots&&\vdots\\\\a_{n1}&&a_{n2}&&\dots&&a_{nn}\end{bmatrix};\quad X=[x_1,x_2,\dots,x_n]^T,求\frac{\mathrm{d}f(x)}{\mathrm{d}X} f(x)=XTAX;A= a11a21⋮an1a12a22⋮an2…………a1na2n⋮ann ;X=[x1,x2,…,xn]T,求dXdf(x)
f ( x ) = ∑ i = 1 N ∑ j = 1 N a i j x i x j f(x)=\sum_{i=1}^N\sum_{j=1}^Na_{ij}x_ix_j f(x)=i=1∑Nj=1∑Naijxixj
- 标量不变,YX拉伸术,X纵向拉伸
d f ( x ) d X = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\\\\frac{\partial f(x)}{\partial x_2}\\\\\vdots\\\\\frac{\partial f(x)}{\partial x_n}\end{bmatrix} dXdf(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)
∂ f ( x ) ∂ x i = [ a i 1 a i 2 … a i n ] [ x 1 x 2 ⋮ x n ] + [ a 1 i a 2 i … a n i ] [ x 1 x 2 ⋮ x n ] \frac{\partial f(x)}{\partial x_i}=\begin{bmatrix}a_{i1}&a_{i2}&\dots&a_{in}\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix}+\begin{bmatrix}a_{1i}&a_{2i}&\dots&a_{ni}\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix} ∂xi∂f(x)=[ai1ai2…ain] x1x2⋮xn +[a1ia2i…ani] x1x2⋮xn
d f ( x ) d X = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ … ⋮ a n 1 a n 2 … a n n ] [ x 1 x 2 ⋮ x n ] + [ a 11 a 21 … a n 1 a 12 a 22 … a n 2 ⋮ ⋮ … ⋮ a 1 n a 2 n … a n n ] [ x 1 x 2 ⋮ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}a_{11}&a_{12}&\dots&a_{1n}\\\\a_{21}&a_{22}&\dots&a_{2n}\\\\\vdots&\vdots&\dots&\vdots\\\\a_{n1}&a_{n2}&\dots&a_{nn}\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix}+\begin{bmatrix}a_{11}&a_{21}&\dots&a_{n1}\\\\a_{12}&a_{22}&\dots&a_{n2}\\\\\vdots&\vdots&\dots&\vdots\\\\a_{1n}&a_{2n}&\dots&a_{nn}\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix} dXdf(x)= a11a21⋮an1a12a22⋮an2…………a1na2n⋮ann x1x2⋮xn + a11a12⋮a1na21a22⋮a2n…………an1an2⋮ann x1x2⋮xn - 已知 A , A T A,A^T A,AT表示如下:
A = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ … ⋮ a n 1 a n 2 … a n n ] ; A T = [ a 11 a 21 … a n 1 a 12 a 22 … a n 2 ⋮ ⋮ … ⋮ a 1 n a 2 n … a n n ] A=\begin{bmatrix}a_{11}&a_{12}&\dots&a_{1n}\\\\a_{21}&a_{22}&\dots&a_{2n}\\\\\vdots&\vdots&\dots&\vdots\\\\a_{n1}&a_{n2}&\dots&a_{nn}\end{bmatrix}\quad;A^T=\begin{bmatrix}a_{11}&a_{21}&\dots&a_{n1}\\\\a_{12}&a_{22}&\dots&a_{n2}\\\\\vdots&\vdots&\dots&\vdots\\\\a_{1n}&a_{2n}&\dots&a_{nn}\end{bmatrix} A= a11a21⋮an1a12a22⋮an2…………a1na2n⋮ann ;AT= a11a12⋮a1na21a22⋮a2n…………an1an2⋮ann - 综上所述如下:
当 f ( x ) = X T A X f(x)=X^TAX f(x)=XTAX时
d f ( x ) d X = A X + A T X = ( A + A T ) X \frac{\mathrm{d}f(x)}{\mathrm{d}X}=AX+A^TX=(A+A^T)X dXdf(x)=AX+ATX=(A+AT)X
相关文章:

矩阵求导笔记
文章目录 1. ML中为什么需要矩阵求导2. 向量函数与矩阵求导初印象3. YX 拉伸术3.1 f(x)为标量,X为列向量3.2 f(x)为列向量,X 为标量3.3 f(x)为列向量,X 为列向量 4. 常见矩阵求导公式4.1 Y A T X YA^TX YATX4.2 Y X T A X YX^TAX YXTAX 1…...

全量知识系统问题及SmartChat给出的答复 之19 关于演示模板
Q.60 可参考的演示模版 (word-def occupiedinterest 5type EBsubclass SEBtemplate (script $Demonstrateactor nilobject nildemands nilmethod (scene $Occupyactor nillocation nil))fill (((actor) (top-of *actor-stack*))((method actor) (t…...
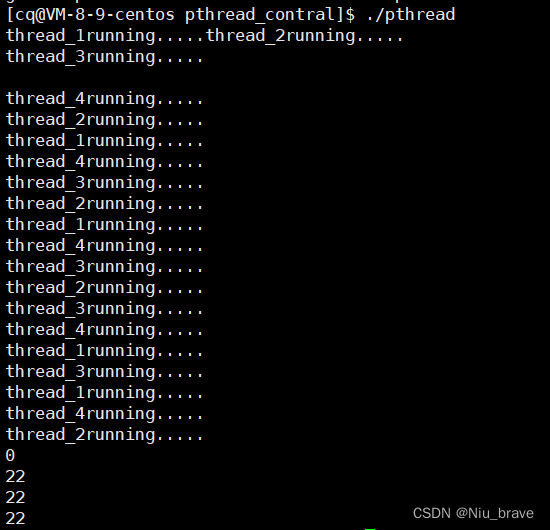
Linux学习——线程的控制
目录 编辑 一,线程的创建 二,线程的退出 1,在子线程内return 2,使用pthread_exit(void*) 三,线程等待 四,线程获取自己的id值 五,线程取消 六,线程分离 一,线程的创建 在对…...

Rust常用特型之Drop特型
Rust常用特型之Drop特型.md在Rust标准库中,存在很多常用的工具类特型,它们能帮助我们写出更具有Rust风格的代码。 今天,我们主要学习Drop特型。 (注:本文更多的是对《Programing Rust 2nd Edition》的自己翻译和理解&…...

嵌入式 Linux 学习
在学习嵌入式 Linux 之前,我们先来了解一下嵌入式 Linux 有哪些东西。 1. 嵌入式 Linux 的组成 嵌入式 Linux 系统,就相当于一套完整的 PC 软件系统。 无论你是 Linux 电脑还是 windows 电脑,它们在软件方面的组成都是类似的。 我们一开电…...
Makedown语法
这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…...

SQLite语句
1.重写SQLiteOpenHelper // 例. public class MySQLiteOpenHelper extends SQLiteOpenHelper {public MySQLiteOpenHelper(Nullable Context context, Nullable String name, Nullable SQLiteDatabase.CursorFactory factory, int version) {super(context, name, factory, ve…...

Spring揭秘:Aware接口应用场景及实现原理!
内容概要 Aware接口赋予了Bean更多自感知的能力,通过实现不同的Aware接口,Bean可以轻松地获取到Spring容器中的其他资源引用,像ApplicationContext、BeanFactory等。 这样不仅增强了Bean的功能,还提高了代码的可维护性和扩展性&…...
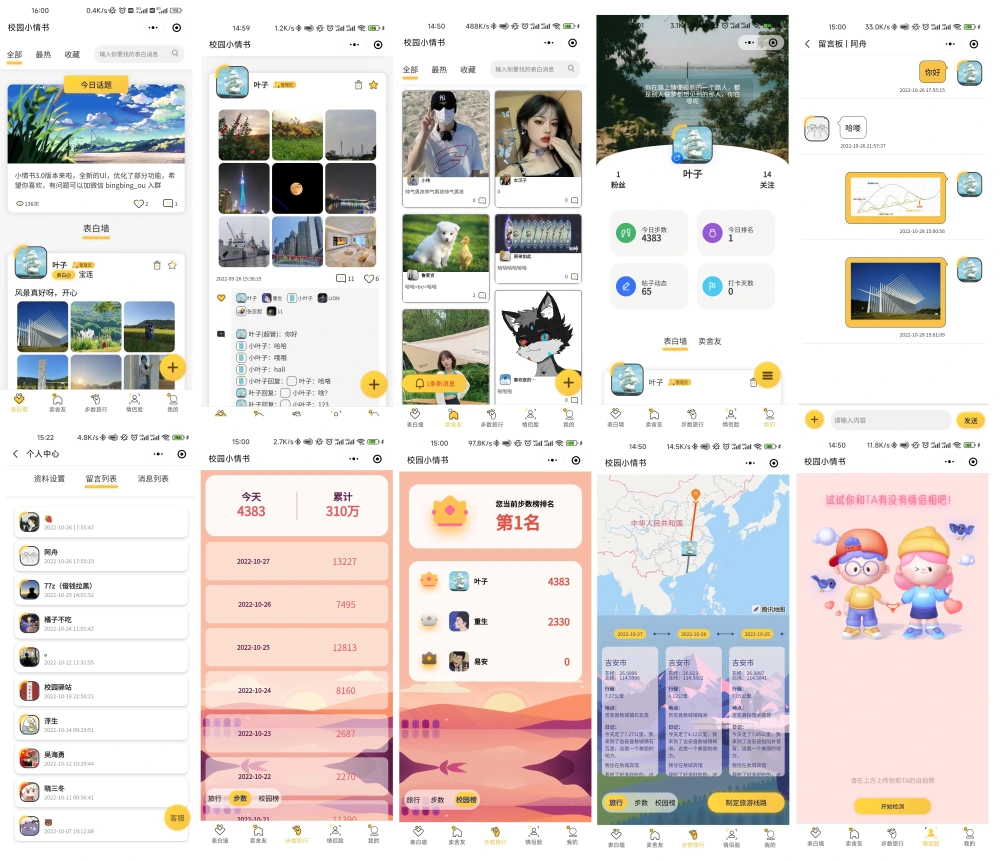
校园小情书微信小程序,社区小程序前后端开源,校园表白墙交友小程序
功能 表白墙卖舍友步数旅行步数排行榜情侣脸漫画脸个人主页私信站内消息今日话题评论点赞收藏 效果图...

从Pandas到Polars :数据的ETL和查询
对于我们日常的数据清理、预处理和分析方面的大多数任务,Pandas已经绰绰有余。但是当数据量变得非常大时,它的性能开始下降。 本文将介绍如何将日常的数据ETL和查询过滤的Pandas转换成polars。 图片 Polars的优势 Polars是一个用于Rust和Python的Data…...

Node.Js编码注意事项
Node.js 中不能使用 BOM 和 DOM 的 API,可以使用 console 和定时器 APINode.js 中的顶级对象为 global,也可以用 globalThis 访问顶级对象 浏览器端js的组成 Node.js中的JavaScript组成 相比较之下发现只有console与定时器是两个API所共有的ÿ…...

floodfill算法题目
前言 大家好,我是jiantaoyab,在下面的题目中慢慢体会floodFill算法,虽然是新的算法,但是用的思想和前面的文章几乎一样,代码格式也几乎一样,但不要去背代码 图像渲染 https://leetcode.cn/problems/flood…...

AI相关的实用工具分享
AI实用工具大赏:赋能科研与生活,探索AI的无限可能 前言 在数字化浪潮汹涌而至的今天,人工智能(AI)已经渗透到我们生活的方方面面,无论是工作还是生活,都在悄然发生改变。AI的崛起不仅为我们带…...

K8s — PVC|PV Terminating State
在本文中,我们将讨论PV和PVC一直Terminating的状态。 何时会Terminting? 在以下情况下,资源将处于Terminating状态。 在删除Bounded 状态的PVC之前,删除了对应的PV,PV在删除后是Terminting状态。删除PVC时,仍有引用…...
C语言 --- 指针(5)
目录 一.sizeof和strlen对比 1.sizeof 2.strlen 3.strlen 和sizeof的对比 二.数组和指针笔试题目详解 回顾:数组名的理解 1.一维数组 2.字符数组 代码1: 代码2: 代码3: 代码4: 代码5: 代码6&am…...
Android Studio Iguana | 2023.2.1版本
Android Gradle 插件和 Android Studio 兼容性 Android Studio 构建系统基于 Gradle,并且 Android Gradle 插件 (AGP) 添加了一些特定于构建 Android 应用程序的功能。下表列出了每个版本的 Android Studio 所需的 AGP 版本。 如果特定版本的 Android Studio 不支持…...

并查集(蓝桥杯 C++ 题目 代码 注解)
目录 介绍: 模板: 题目一(合根植物): 代码: 题目二(蓝桥幼儿园): 代码: 题目三(小猪存钱罐): 代码: …...
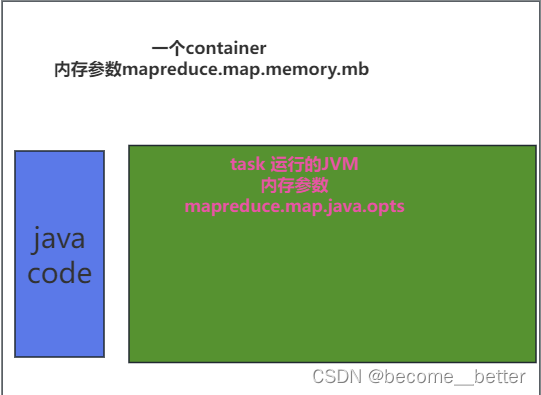
MapReduce内存参数自动推断
MapReduce内存参数自动推断。在Hadoop 2.0中,为MapReduce作业设置内存参数非常繁琐,涉及到两个参数:mapreduce.{map,reduce}.memory.mb和mapreduce.{map,reduce}.java.opts,一旦设置不合理,则会使得内存资源浪费严重&a…...

pyside6 pytq PyDracula QVideoWidget视频只有画面没有声音
解决方案: 先不使用框架,纯pyside6代码,如果添加视频有画面有声音,那可以排除是硬件问题,如果没有画面只有声音,可能是视频解码器无法解码,换个格式的视频文件如果只有使用PyDracula 出问题&am…...
Axure基础 各元件的作用及介绍
图像热区 增加按钮或者文本的点击区域,他是透明的,在预览时看不见。 动态面板 用来绘制一下带交互效果的元件,他是动态的,如轮播图,一个动态面板里可以有多个子面板,每一个子面板对应着不同的效果。 他…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
