算法D43 | 动态规划5 | 1049. 最后一块石头的重量 II 494. 目标和 474.一和零
1049. 最后一块石头的重量 II
本题就和 昨天的 416. 分割等和子集 很像了,可以尝试先自己思考做一做。
视频讲解:动态规划之背包问题,这个背包最多能装多少?LeetCode:1049.最后一块石头的重量II_哔哩哔哩_bilibili
代码随想录
Python:
class Solution:def lastStoneWeightII(self, stones: List[int]) -> int:total = sum(stones)target = total//2dp = [0] * (target+1)for stone in stones:for j in range(target, stone-1, -1):dp[j] = max(dp[j], dp[j-stone]+stone)return total - dp[target] - dp[target]C++:
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int total = 0;for (int i=0; i<stones.size(); i++) total += stones[i];int target = total/2;vector<int> dp(target+1, 0);for (int i=0; i<stones.size(); i++) {for (int j=target; j>=stones[i]; j--) {dp[j] = max(dp[j], dp[j-stones[i]]+stones[i]);}}return total - dp[target] - dp[target];}
};494. 目标和
大家重点理解 递推公式:dp[j] += dp[j - nums[i]],这个公式后面的提问 我们还会用到。
视频讲解:动态规划之背包问题,装满背包有多少种方法?| LeetCode:494.目标和_哔哩哔哩_bilibili
代码随想录
Python:
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:total = sum(nums)if (target + total)%2 == 1: return 0if (abs(target)>total): return 0bagSize = (target + total)//2dp = [0] * (bagSize+1)dp[0] = 1for num in nums:for j in range(bagSize, num-1, -1):dp[j] += dp[j-num]return dp[bagSize]C++:
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int total = 0;for (int i:nums) total+=i;if (abs(target) > total) return 0;if ((target+total)%2 == 1) return 0;int bagSize = (total+target)/2;vector<int> dp(bagSize+1, 0);dp[0] = 1;for (int i=0; i<nums.size(); i++) {for (int j=bagSize; j>=nums[i]; j--) {dp[j] += dp[j-nums[i]];}}return dp[bagSize];}
};474.一和零
通过这道题目,大家先粗略了解, 01背包,完全背包,多重背包的区别,不过不用细扣,因为后面 对于 完全背包,多重背包 还有单独讲解。
视频讲解:动态规划之背包问题,装满这个背包最多用多少个物品?| LeetCode:474.一和零_哔哩哔哩_bilibili
代码随想录
Python:
class Solution:def findMaxForm(self, strs: List[str], m: int, n: int) -> int:dp = [[0]*(n+1) for _ in range(m+1)]for s in strs:one_num = s.count('1')zero_num = len(s) - one_numfor i in range(m, zero_num-1, -1):for j in range(n, one_num-1, -1):dp[i][j] = max(dp[i][j], dp[i-zero_num][j-one_num]+1)return dp[m][n]C++:
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m+1, vector<int>(n+1, 0));for (string str : strs) {int oneNum = 0, zeroNum = 0;for (char ch : str) {if (ch == '0') zeroNum++;else oneNum++;}for (int i=m; i>=zeroNum; i--) {for (int j=n; j>=oneNum; j--) {dp[i][j] = max(dp[i][j], dp[i-zeroNum][j-oneNum]+1);}}}return dp[m][n];}
};相关文章:

算法D43 | 动态规划5 | 1049. 最后一块石头的重量 II 494. 目标和 474.一和零
1049. 最后一块石头的重量 II 本题就和 昨天的 416. 分割等和子集 很像了,可以尝试先自己思考做一做。 视频讲解:动态规划之背包问题,这个背包最多能装多少?LeetCode:1049.最后一块石头的重量II_哔哩哔哩_bilibili 代…...

设计模式—桥接模式
定义: 桥接模式是将抽象部分与它的实现部分分离,使它们都可以独立地变化。它是一种对象结构型模式,又称为柄体(Handle and Body)模式或接口(Interfce)模式。 本章代码:小麻雀icknn/设计模式练习 - Gitee.com 结构: 抽象化(Abstraction)角色:…...

伊萨卡训练代码
我们建议创建并激活 conda 环境,以确保在下面安装正确的软件包版本的干净环境。 # Optional but recommended: conda create -n ithaca python3.9 conda activate ithaca 克隆此存储库并进入其根目录。通过以下方式安装完整的 ithaca 依赖项(包括训练&am…...

视频产品介绍:AS-VCVR-N多协议视频接入网关
目 录 一、产品概述 (一)非标设备接入 (二)信令流转换 (三)媒体流转发 二、网关特性 三、技术参数 一、产品概述 视频接入网关服务是终端用户与视频源的传输枢纽,实现把前端不同…...
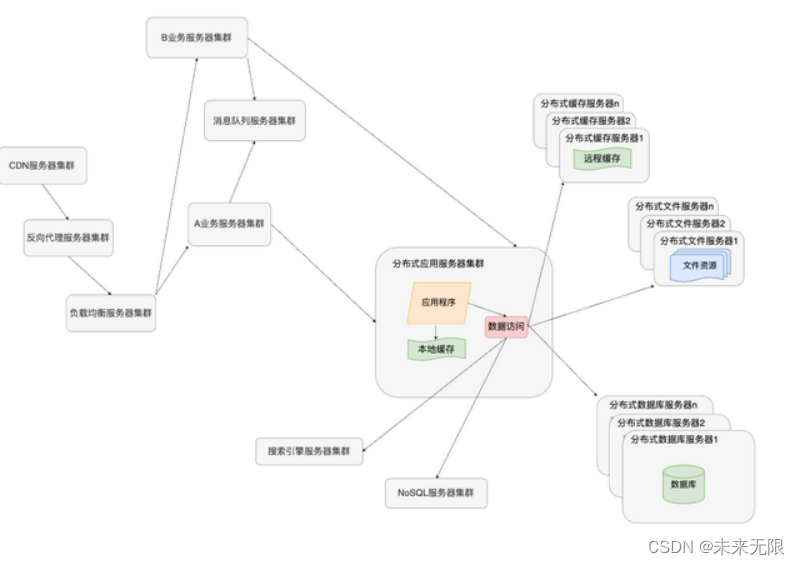
大型网站架构演化总结
本文图解大型网站架构演化。 目录 1、单一应用服务阶段 2、应用与数据服务分离阶段 3、利用缓存提高性能阶段 4、应用服务集群阶段 5、数据库读写分离阶段 6、反向代理与CDN加速阶段 7、分布式数据库阶段 8、 NoSQL与搜索引擎阶段 9、业务拆分阶段 10、分布式服务阶…...

5G智能制造纺织工厂数字孪生可视化平台,推进纺织行业数字化转型
5G智能制造纺织工厂数字孪生可视化平台,推进纺织行业数字化转型。纺织工业作为传统制造业的重要组成部分,面临着转型升级的紧迫需求。随着5G技术的快速发展,智能制造成为纺织工业转型升级的重要方向。数字孪生可视化平台作为智能制造的核心技…...

仿牛客网项目---Elasticsearch分布式搜索引擎
1.什么是ElasticSearch分布式搜索引擎? Elasticsearch是一个开源的分布式搜索引擎,提供实时的、高可用性的搜索和分析解决方案。它支持快速索引和搜索大规模数据,具有分布式架构、RESTful API、基于JSON的查询语言等功能,适用于各…...

macbook pro 2018 安装 arch linux 双系统
文章目录 友情提醒关于我的 mac在 mac 上需要提前做的事情复制 wifi 驱动 在 linux 上的操作还原 wifi 驱动连接 wifi 网络磁盘分区制作文件系统挂载分区 使用 archinstall 来安装 arch linux遗留问题 友情提醒 安装 archl linux 的时候,mac 的键盘是没法用的&#…...

虚拟机安装CentOS教学,超详细一步安装到底!
首先将Centos的镜像文件进行下载,随后再进行安装配置: https://mirrors.tuna.tsinghua.edu.cn/centos-vault/7.8.2003/isos/x86_64/CentOS-7-x86_64-DVD-2003.iso 1.打开VMware,新建虚拟机,选择典型安装,点击下一步 2.选择稍…...

“2024杭州智慧城市及安防展会”将于4月在杭州博览中心盛大召开
2024杭州国际智慧城市及安防展览会,将于4月24日在杭州国际博览中心盛大开幕。这场备受瞩目的盛会,不仅汇集了全球智慧城市与安防领域的顶尖企业,更是展示最新技术、交流创新理念的重要平台。近日,从组委会传来消息,展会…...

【C++庖丁解牛】模拟实现STL的string容器(最后附源码)
📙 作者简介 :RO-BERRY 📗 学习方向:致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 📒 日后方向 : 偏向于CPP开发以及大数据方向,欢迎各位关注,谢谢各位的支持 目录 1.vs和g下string结构…...
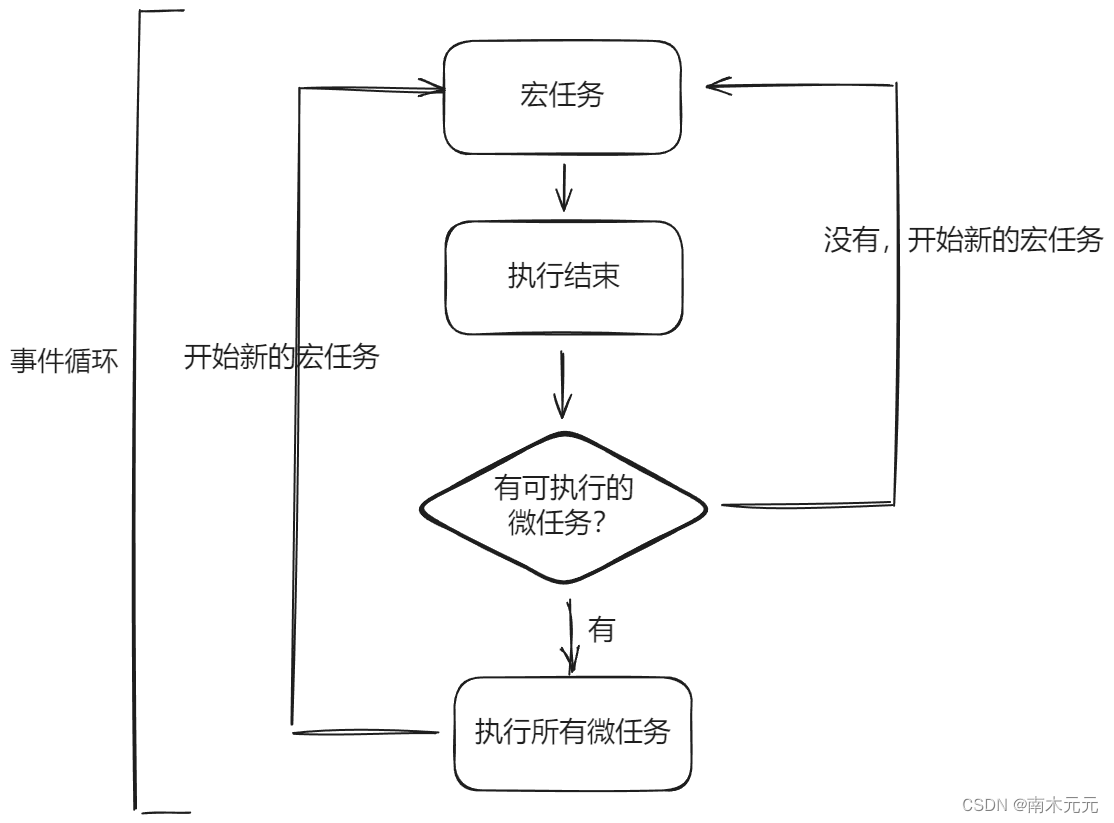
不要在代码中随便使用try...catch了
前言 📫 大家好,我是南木元元,热爱技术和分享,欢迎大家交流,一起学习进步! 🍅 个人主页:南木元元 目录 背景 js中的try...catch try...catch运行机制 js的事件循环机制 try...c…...

网络编程(3/6)
使用C语言完成数据库的增删改 #include<myhead.h> int do_add(sqlite3 *ppDb) {int numb;char name[50];int salary;printf("请输入员工信息:工号、姓名、薪水\n");scanf("%d %s %d",&numb,name,&salary);char sql[128];char *e…...
(day 2)JavaScript学习笔记(基础之变量、常量和注释)
概述 这是我的学习笔记,记录了JavaScript的学习过程,我是有一些Python基础的,因此在学习的过程中不自觉的把JavaScript的代码跟Python代码做对比,以便加深印象。我本人学习软件开发纯属个人兴趣,大学所学的专业也非软件…...
Spring Boot中全局异常处理器
文章目录 1.Spring Boot中两种异常处理方式2.为什么需要全局异常处理呢?3. 全局异常处理器测试4.ControllerAdvice 详解5.ExceptionHandler 详解 1.Spring Boot中两种异常处理方式 要想解决测试中存在的问题,我们需要对程序中可能出现的异常进行捕获&am…...

【JAVA重要知识 | 第七篇】Java异常知识总结(声明、抛出、捕获异常)
7.Java异常知识总结(声明、抛出、捕获异常) 7.1异常定义 在程序运行过程中,如果JVM检测出一个不可能执行的操作时,就会出现运行时错误(runtime error)。在Java中,运行时错误会作为异常抛出。异…...
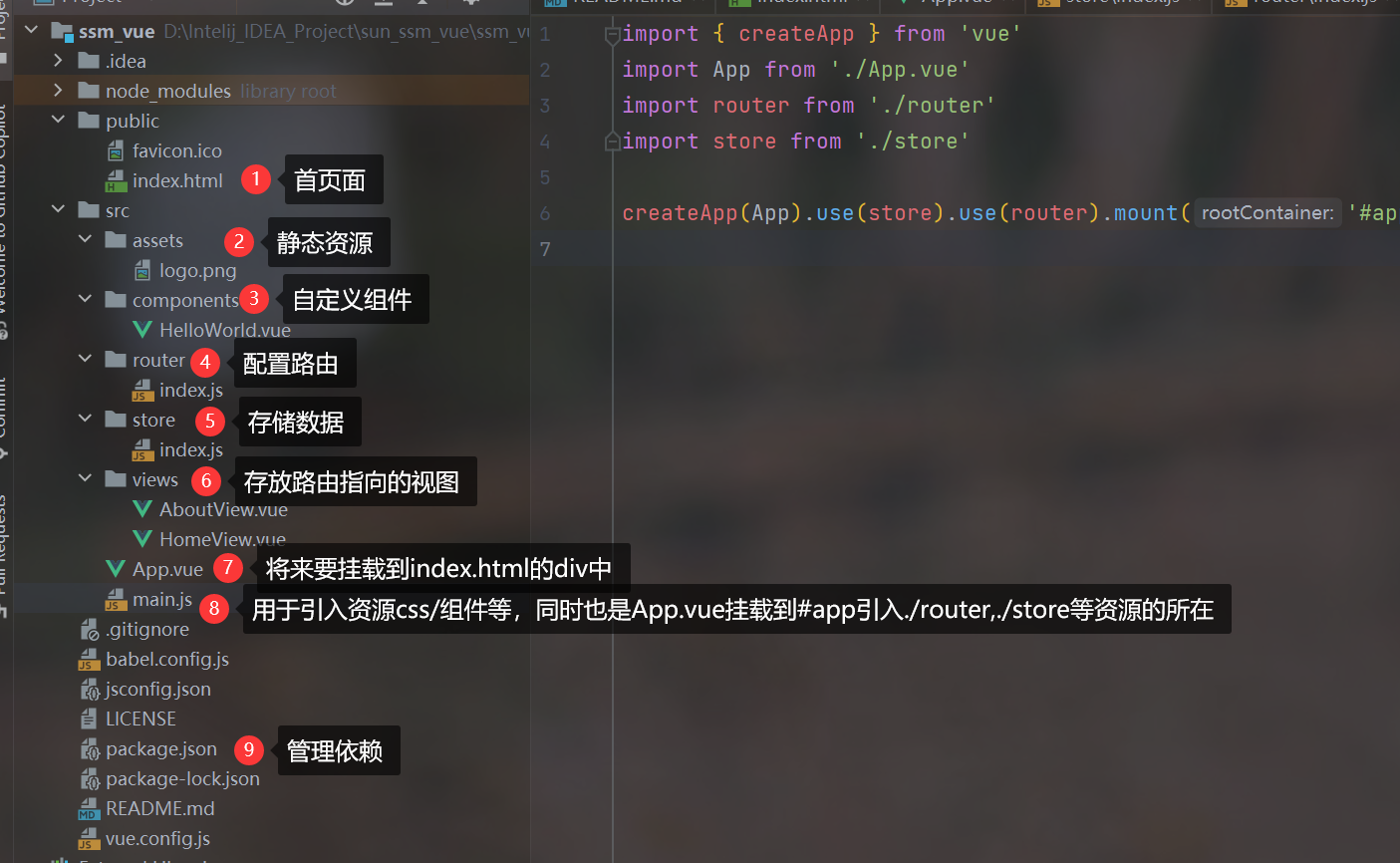
SSM整合项目(Vue3环境搭建)
SSM整合项目(Vue3环境搭建) 1.下载node.js 1.卸载原来的node.js 2.检测是否卸载成功 3.下载node.js(10.16.3) 一路next就可以 4.检测是否安装成功 2.全局安装Vue插件cli 命令行输入 npm install -g vue/cli 3.新建Vue项目 1.…...

Golang 方法的接收器 receiver 指针和值的区别
一、如果receiver是指针类型 package mainimport "fmt"type Count struct {count int }func main() {c : Count{count: 0}c.incr()fmt.Println(c.count)c2 : &cc2.incr()fmt.Println(c2.count) }func (c *Count) incr() {c.count }//打印结果 1 2 incr 方法的 …...

【蓝桥杯】节省时间
一、对于string类型变量的连接,可以直接用“”或者“”来进行字符串的直接连接 string a"1"; string b"2"; string c; cab"12"; string操作符两边既可以都是string类型,也可是string与char类型 注意: (1)“”…...
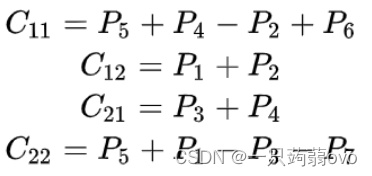
矩阵乘法--Strassen算法
一、矩阵乘法 从中可以看出,计算两个矩阵的乘积,需要三个 for 循环,可以简单写出代码: for(int i1;i<m;i)for(int j1;j<p;j)for(int k1;k<n;k)c[i][j]a[i][k]*b[k][j]; 时间复杂度的分析:很明显,…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
