矩阵乘法--Strassen算法
一、矩阵乘法

从中可以看出,计算两个矩阵的乘积,需要三个 for 循环,可以简单写出代码:
for(int i=1;i<=m;i++)for(int j=1;j<=p;j++)for(int k=1;k<=n;k++)c[i][j]+=a[i][k]*b[k][j];时间复杂度的分析:很明显,三层for循环迭代,复杂度为
二、Straasen 算法
与简单的矩阵乘法计算不同,Strassen算法通过分治操作将运行变快,时间复杂度为
1.Strassen 算法的原理:


简单的计算备用矩阵和式 :通过简单的两层for循环将其加减
备用的乘积: 递归调用strassen算法,因为已逐步构造好分块的A和S矩阵,将需要的矩阵作为strassen的输入,就可以得出P矩阵
最后计算将C矩阵的四个分矩阵求出,再合并求得最后的C矩阵

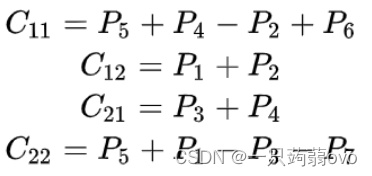
①矩阵相加减:
void plus(int **matrixa,int **matrixb,int **matrixc, int x) // 矩阵相加
{for(int i=1;i<=x;i++)for(int j=1;j<=x;j++)matrixc[i][j]=matrixa[i][j]+matrixb[i][j];
}
void cut(int **matrixa,int **matrixb,int **matrixc,int x1) // 矩阵相减
{for(int i=1;i<=x1;i++)for(int j=1;j<=x1;j++)matrixc[i][j]=matrixa[i][j]-matrixb[i][j];
}② 矩阵的拆分(将一个矩阵分成四个小矩阵)与合并:
for(int i=1;i<=newx;i++)
for(int j=1;j<=newx;j++)
{ a11[i][j]=ma[i][j];a12[i][j]=ma[i][j+newx];a21[i][j]=ma[i+newx][j];a22[i][j]=ma[i+newx][j+newx];b11[i][j]=mb[i][j];b12[i][j]=mb[i][j+newx];b21[i][j]=mb[i+newx][j];b22[i][j]=mb[i+newx][j+newx];
}for(int i=1;i<=newx;i++)
for(int j=1;j<=newx;j++)
{mc[i][j]=c11[i][j]; mc[i][j+newx]=c12[i][j];mc[i+newx][j]=c21[i][j];mc[i+newx][j+newx]=c22[i][j];
}③递归调用过程:
strassen(a11,s1,p1,newx);
strassen(s2,b22,p2,newx);
strassen(s3,b11,p3,newx);
strassen(a22,s4,p4,newx);
strassen(s5,s6,p5,newx);
strassen(s7,s8,p6,newx);
strassen(s9,s10,p7,newx);2.关于Strassen算法的理解:
Strassen算法的理论推导是比较难的,或者说,是前人不断的试验发现得出的结果,因此需根据得出的公式打出代码。
代码的难度在于很多地方。
①递归的调用:将预处理的代码通过递归计算出。
②二维矩阵的存储以及二维数组在函数中的传递调用:
因为在递归中的数组是反复调用的,所以一定不能使用全局数组导致计算混乱。
另一个是二维矩阵的定义,不能简单定义静态数组,定义静态数组过大程序无法运行,并且运行速度慢,而应当定义malloc动态数组,数组大小可以改变,而且运行时高效很多。
malloc定义二维动态数组:
c=(int **)malloc(sizeof(int *)*n);
for(int i=1;i<=n;i++)c[i]=(int *)malloc(sizeof(int)*n);三、Strassen 算法的改进
通过上述的理解,可以知道Straasen算法适用于当阶数为 2的幂(或者2的倍数) 时,是否能使其扩大适用范围,让任何相同阶数的矩阵算法都能使用。
当矩阵的阶数为奇数时,只需要将其行列各增加1,并且增加的元素全为0,即可使用 Straasen算法。
改进Strassen算法的复杂度:改进算法并未与原算法发生实质性的改变,因此时间复杂度不发生改变。
相关文章:
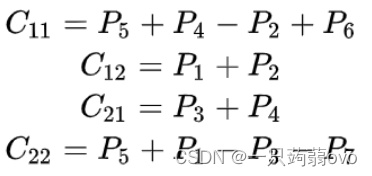
矩阵乘法--Strassen算法
一、矩阵乘法 从中可以看出,计算两个矩阵的乘积,需要三个 for 循环,可以简单写出代码: for(int i1;i<m;i)for(int j1;j<p;j)for(int k1;k<n;k)c[i][j]a[i][k]*b[k][j]; 时间复杂度的分析:很明显,…...

Unity笔记:C#基础(1)
杂项 虚函数 CSDN - C虚函数详解 cnblog - C#中的虚函数virtual 常量池与new 在C#中,string是不可变的,这意味着对string对象的操作通常会返回一个新的string对象,而不会修改原始的string对象。因此,几乎所有涉及更改string内…...

计算机科技与心理学的紧密交织:一场跨学科的深度对话
随着信息技术的飞速发展,计算机科学与心理学这两门看似迥异的学科日益呈现出密不可分的关系。本文将深入探讨计算机科学与心理学之间的相互影响和融合,揭示二者在研究方法、应用实践以及对未来社会发展的影响等方面的高度关联性。 计算机科学为心理学研究…...

【JAVA类】利用接口的多继承实现———图书管理系统【附源码】
引言 在我们学习了一些java的基础语法之后,需要把这些知识点可以串起来,这里使用一个简单的小项目可以很好的帮助我们牢记这些知识点,今天就带大家学习一个有关java的小项目,很多学校也经常把这个项目作为他们的课程设计——经典的…...
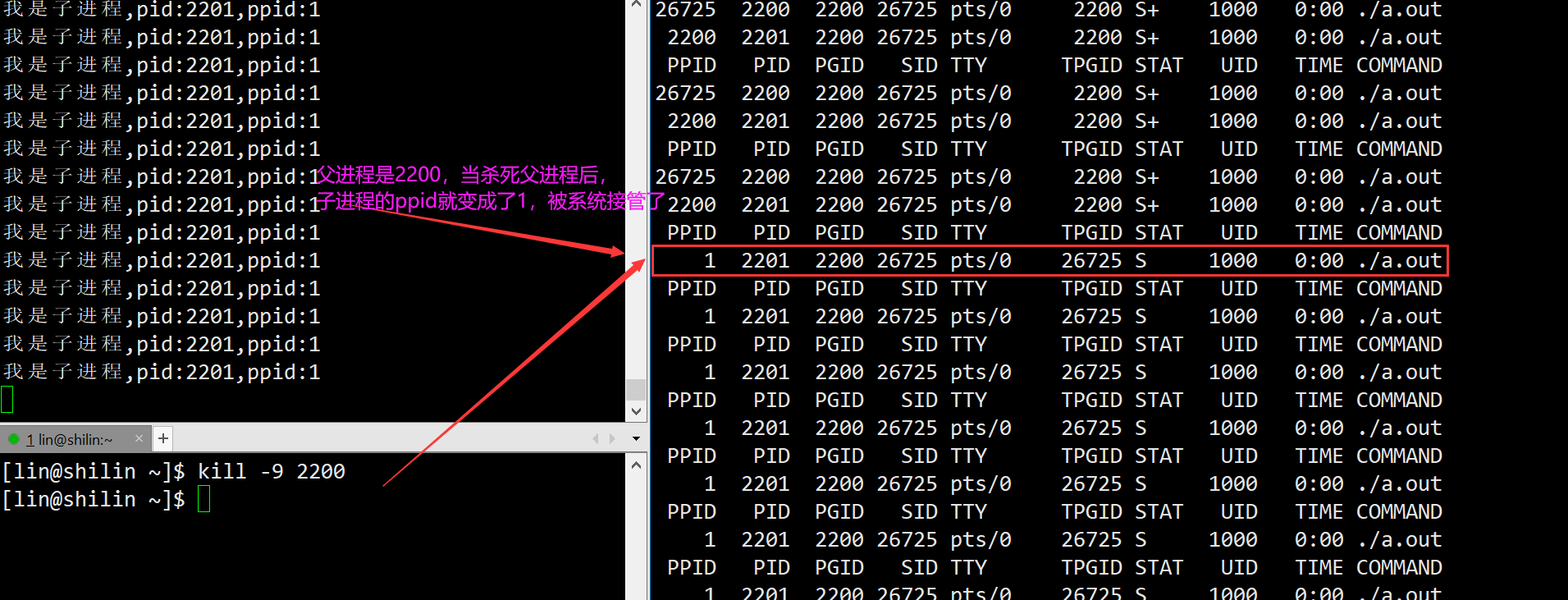
Linux进程概念僵尸进程孤儿进程
文章目录 一、什么是进程二、进程的状态三、Linux是如何做的?3.1 R状态3.2 S状态3.3 D状态3.4 T状态3.5 t状态3.6 X状态3.7 Z状态 四、僵尸进程4.1 僵尸进程危害 五、孤儿进程 一、什么是进程 对于进程理解来说,在Windows上是也可以观察到的,…...

实体店如何引流成交裂变?打造流量新引擎的秘诀
在数字化浪潮席卷的今天,实体店经营面临着前所未有的挑战与机遇。社区店作为连接居民日常生活的桥梁,如何在激烈的市场竞争中脱颖而出,实现引流、成交与裂变,成为摆在每一位实体店创业者面前的重要课题。 作为一名鲜奶吧开店5年的…...
)
蓝桥杯(日期问题纯暴力)
纯纯暴力,写的想吐,玛德服了。 但是复习了vector去重方法,日期的合法性判断。 #include <iostream> #include <vector> #include <cstring> #include <algorithm>using namespace std; vector<int> res; st…...

ES: ES+Kibana 环境部署
ESKibana 部署 机器信息 10.10.8.62 10.10.8.63 10.10.8.64版本选择:6.8.1 基础环境优化 所有节点 # 关闭防火墙 systemctl stop firewalld.service systemctl disable firewalld.service# 查看selinux getenforce # 关闭selinux setenforce 0 # 永久关闭se…...

Find My产品越来越得到市场认可,伦茨科技ST17H6x芯片赋能厂家
苹果发布AirTag发布以来,大家都更加注重物品的防丢,苹果的 Find My 就可以查找 iPhone、Mac、AirPods、Apple Watch,如今的Find My已经不单单可以查找苹果的设备,随着第三方设备的加入,将丰富Find My Network的版图。产…...
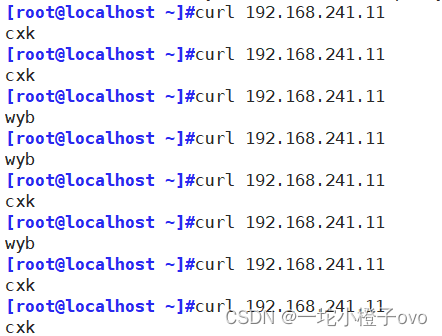
Linux系统——Haproxy高性能负载均衡软件
目录 一、Haproxy介绍 1.Haproxy定义 2.Haproxy主要特性 二、安装Haproxy 1.yum安装 2.第三方rpm包安装 3.编译安装 3.1解决Lua环境 3.2编译安装Haproxy 三、配置文件详解 1.状态页 2.日志管理 2.1定义日志到其他主机站点 3.指定进程线程个数 4.cpu亲缘性 5.多进…...

Python办公自动化之PDF(二)
Python操作PDF二 1、PyMuPDF简介2、 1、PyMuPDF简介 PyMuPDF(也称Fitz)开源,提供了一整套用于处理PDF文件的综合工具。使用PyMuPDF,用户可以高效地执行打开PDF、提取文本、图像和表格、操作旋转和裁剪等页面属性、创建新PDF文档以…...

登录失败重试次数安全设计方案
1、登录失败重试次数设计方案 1、无论是账号还是密码错误,统一提示:用户名或密码错误,账号剩余登录次数N! 2、同一账号连续登录失败5次,锁定该账号5分钟,5分钟后可以再重试登录。 开发设计 keyÿ…...

Django——模板
Django——模板 Django 提供一种动态生成 HTML 页面 —— 模板 1、模板语言 模板语言(DTL): 变量 , 注释 , 标签 , 过滤器 , 模板继承 1、变量 <body> <!-- 这个是前端中的注释 --> {# 这种是Django中模板语言的…...

角蜥优化算法 (Horned Lizard Optimization Algorithm ,HLOA)求解无人机路径优化
一、无人机路径规划模型介绍 无人机三维路径规划是指在三维空间中为无人机规划一条合理的飞行路径,使其能够安全、高效地完成任务。路径规划是无人机自主飞行的关键技术之一,它可以通过算法和模型来确定无人机的航迹,以避开障碍物、优化飞行时间和节省能量消耗。 二、算法介…...
Windows下 OracleXE_21 数据库的下载与安装
Oracle 数据库的下载与安装 数据库安装包下载数据库安装访问数据库进行测试Navicat连接数据库 1. 数据库安装包的下载 1.1 下载地址 Oracle Database Express Edition | Oracle 中国 1.2 点击“下载 Oracle Database XE”按钮,进去到下载页面(选择对…...

新手如何快速上手学习单片机?
读者朋友能容我,不使博文负真心 新开专栏,期待与诸君共享精彩 个人主页:17_Kevin-CSDN博客 专栏:《单片机》 学习单片机是一个有趣且有挑战性的过程。单片机是一种微控制器,广泛应用于各种电子设备和嵌入式系统中。在这…...

grpc的验证器
简介 在使用grpc库时候 ,很多时候我们需要对反序列化的参数进行校验,代码中有很多参数校验的代码,如果手动实现,会非常繁琐,对于grpc来说,在定义proto的时候使用直接定义参数的限制规则是一种更合理、更优雅的方式,插…...

无法找到concrt140.dll怎么办?concrt140.dll丢失的5种解决方法
在我们使用计算机的时候,偶尔会遭遇一些技术问题,其中一个比较常见的问题就是出现了"丢失concrt140.dll文件"的提示。当我们的电脑告诉我们缺少了concrt140.dll文件时,常常是因为某些程序无法找到这个文件而导致了程序的运行异常。…...
Elasticsearch 分享
一、Elasticsearch 基础介绍 ElasticSearch 是分布式实时搜索、实时分析、实时存储引擎,简称(ES), 成立于2012年,是一家来自荷兰的、开源的大数据搜索、分析服务提供商,为企业提供实时搜索、数据分析服务,…...

cpu masks的初始化
在内核中,有几个位图变量是用作标识cpu数量和状态的,它们分别是: 变量名称用途循环所使用的宏cpu_possible_mask系统中有多少个可以运行的cpu核for_each_possible_cpucpu_present_mask系统中有多少个可处于运行状态的cpu核for_each_present_…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
