数据结构---复杂度(2)
1.斐波那契数列的时间复杂度问题


每一行分别是2^0---2^1---2^2-----2^3-------------------------------------------2^(n-2)

利用错位相减法,可以得到结果是,2^(n-1)-1,其实还是要减去右下角的灰色部分,我们可以拿简单的数字进行举例子,右下角会先变为2,1;例如
5
4 3
3 2 2 1
2 1
这个例子就可以看出来:左下角还有数据的时候,右下角就已经可以得出结果了,但是随着n的增加,这个右下角的影响对整体越来越小,所以我们可以忽略,我们只需要关注计算次数的数量级,所以,斐波那契数列的复杂度就是2^n;
2.空间复杂度
算法运行占用的额外的空间的一种量度
系统自己开辟的空间不属于空间复杂度的范畴,我们自己开辟的空间才属于空间复杂度
斐波那契数列的空间复杂度是O(N),递归开辟函数栈帧,回调的时候函数栈帧继续利用以后才会销毁,但是这个过程时间是累积的;所以时间累加,空间重复利用;
所以:时间是一去不复返的,空间是可以重复利用的;
3.函数栈帧的进一步理解

栈帧的销毁是归还使用权,还给了操作系统,并不是真正的销毁,main函数开辟函数栈帧,调用func1函数以后开辟新的栈帧,使用完之后栈帧销毁,func2开辟的还是func1的这块空间,所以打印的地址一样;归还栈帧以后其他的函数还是可以使用的;
这个时候,再来看看斐波那契数列,他调用的过程是return fib(n-1)+fib(n-2),他会先调用左边的n-1,,接着调用下一个n-1,他在调用完成以后,回调剩下的n-2的时候和原来使用的栈帧地址是一样的,这样就减少了空间复杂度,开辟的空间最后都会销毁,空间复杂度计算的是占用空间最多时候的情况;
4.轮转数组带你认识复杂度

(1)我们可以使用3次逆置的做法

这个做法的时间复杂度是O(N),空间复杂度是O(1);关键是对于节点处的数据下标的控制,先让左边
逆置,再让右边逆置,最后整体进行倒序;
(2)调用库函数memcpy
这个做法就是拿空间换时间,需要多开辟数组空间,这个里面的时间,空间复杂度都是O(N);
相关文章:

数据结构---复杂度(2)
1.斐波那契数列的时间复杂度问题 每一行分别是2^0---2^1---2^2-----2^3-------------------------------------------2^(n-2) 利用错位相减法,可以得到结果是,2^(n-1)-1,其实还是要减去右下角的灰色部分,我们可以拿简单的数字进行举例子&…...

【设计模式】设计原则和常见的23种经典设计模式
设计模式 1. 设计原则(记忆口诀:SOLID)【记忆口诀:单开里依接迪合(单开礼仪接地和)】 (1)单一职责原则(Single Responsibility Principle, SRP) ÿ…...
Spring Cloud Gateway自定义断言
问题:Spring Cloud Gateway自带的断言(Predicate)不满足业务怎么办?可以自定义断言! 先看Spring Cloud Gateway是如何实现断言的 Gateway中断言的整体架构如下: public abstract class AbstractRoutePred…...

智能测径仪在胶管行业的应用
关键字:胶管外径尺寸测量,胶管检测仪器,胶管外径检测,高温胶管外径检测,软硬胶管检测, 智能测径仪在家胶管行业中的应用主要体现在对胶管外径的精确测量和控制上。在胶管生产过程中,外径的大小直…...
vue自定义主题皮肤方案
方案一:CSS变量换肤(推荐) 利用css定义变量的方法,用var在全局定义颜色变量(需将变量提升到全局即伪类选择器 :root)然后利用js操作css变量,document.getElementsByTagName(‘body’)[0].style…...

iOS中使用schema协议调用APP和使用iframe打开APP的例子
大家好我是咕噜美乐蒂,很高兴又和大家见面了! 当调用自定义 URL scheme 或使用 iframe 打开应用程序时,可以采取以下详细步骤: 使用自定义 URL scheme 协议调用应用程序 1.首先,确认目标应用程序已经注册了自定义 U…...

2024.3.11
提示并输入一个字符串,统计该字符中大写、小写字母个数、数字个数、空格个数以及其他字符个数 #include <iostream> #include<string> using namespace std;int main() {cout << "please input a string:" << endl;string str;g…...

Web服务器需要警惕的一些安全隐患
Web服务器需要警惕的一些安全隐患有哪些,今天德迅云安全就带您来了解下。熟悉了解了就知道怎么规避风险。不过无论是什么漏洞,都体现着安全是一个整体的真理,考虑Web服务器的安全性,必须要考虑到与之相配合的操作系统。 1.物理路径…...
MinGW-w64的下载与安装
文章目录 1 下载2 安装3 配置环境变量4 验证 1 下载 官网地址:https://www.mingw-w64.org/github地址:https://github.com/niXman/mingw-builds-binaries/releases windows下载 跳转github下载 版本号选择:13.2.0是GCC的版本号;…...

docker使用笔记
查看本机上所有镜像 docker images打包项目(打包完成后自动载入镜像) The command docker build -t search-server . you provided is a standard way to build a Docker image. The -t flag tags the resulting image, and search-server is the tag …...

新规正式发布 | 百度深度参编《生成式人工智能服务安全基本要求》
2024年2月29日,全国网络安全标准化技术委员会( TC260 )正式发布《生成式人工智能服务安全基本要求》(以下简称《基本要求》)。《基本要求》规定了生成式人工智能服务在安全方面的基本要求,包括语料安全、模…...

2024年AI辅助研发的趋势和影响
摘要:随着人工智能技术的迅猛发展,2024年AI辅助研发正成为科技界和工业界的瞩目焦点。本文将探讨AI辅助研发在各个领域的应用和影响,并展望2024年AI辅助研发的趋势。 引言 随着人工智能技术的不断进步,AI辅助研发正逐渐渗透到各…...

2k_Day1:今天是设计模式的大白话1
大白话: 原则有一点很难做到,就是定义好的类,只能加不能改(开放-关闭原则) 1.工厂模式就是,比如你定了一个汽车接口,然后小车、中车、大车都继承这个接口,这时,定一个汽…...
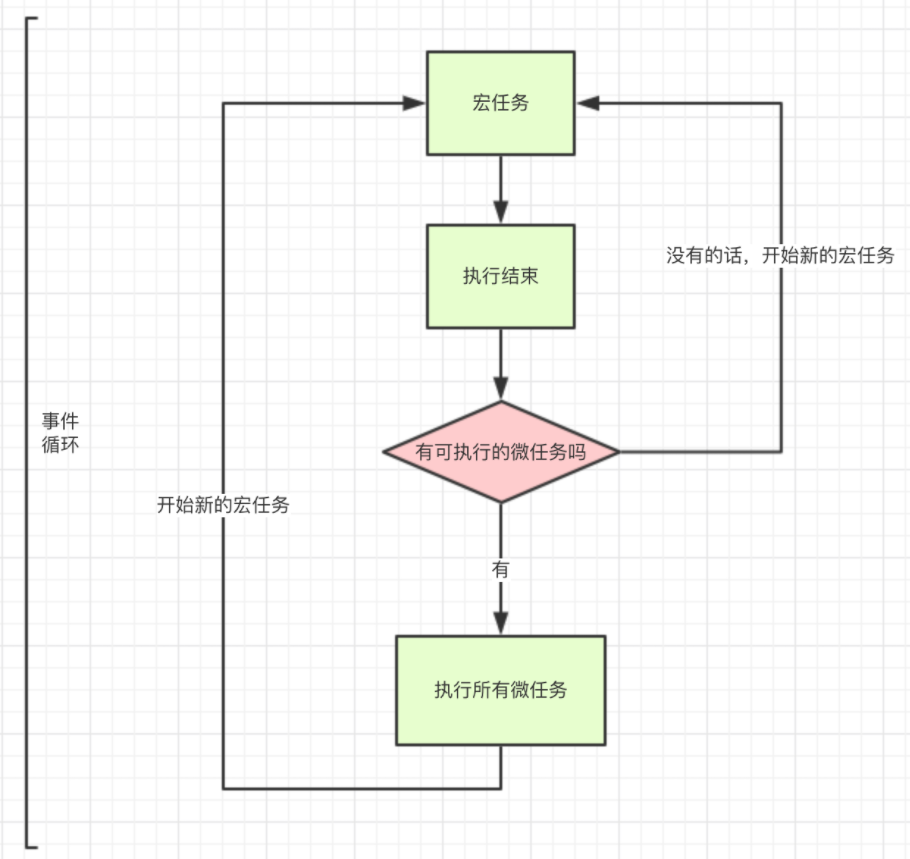
面试官:说说你对事件循环的理解
一、事件循环是什么 首先,JavaScript是一门单线程的语言,意味着同一时间内只能做一件事,但是这并不意味着单线程就是阻塞,而实现单线程非阻塞的方法就是事件循环 在JavaScript中,所有的任务都可以分为 同步任务&#…...

【SpringCloud微服务实战03】Nacos 注册中心
一、Nacos安装 官方文档安装Nacos教程:Nacos 快速开始 这里安装的是1.4.7版本,安装之后访问http://127.0.0.1:8848/nacos 管理界面如下:(用户名:nacos,密码:nacos) 二、Nacos服务注册和发现 1、在父工程中配置文件pom.xml 中添加spring-cloud-alilbaba的管理依赖:…...

FLatten Transformer_ Vision Transformer using Focused Linear Attention
paper: https://arxiv.org/abs/2308.00442 code: https://github.com/LeapLabTHU/FLatten-Transformer 摘要 当将transformer模型应用于视觉任务时,自注意的二次计算复杂度( n 2 n^2 n2)一直是一个持续存在的挑战。另一方面,线性注意通过精心设计的映射…...

STM32CubeMX学习笔记17--- FSMC
1.1 TFTLCD简介 TFT-LCD(thin film transistor-liquid crystal display)即薄膜晶体管液晶显示器。液晶显示屏的每一个像素上都设置有一个薄膜晶体管(TFT),每个像素都可以通过点脉冲直接控制,因而每个节点都…...
)
【MogDB】实战MogDB数据库适配Halo博客系统1.6版本(基于springframework+hibernate+HikariPool)
前言 前一篇文章说了MogDB适配Halo,【MogDB】将流行的博客系统Halo后端的数据库设置为MogDB,但是适配的是2.x版本,由于2.x版本已经引入了对postgresql的支持,而MogDB对于postgresql有很好的兼容性,因此适配起来很简单。但是由于halo2.x的版本…...

Python与FPGA——局部二值化
文章目录 前言一、局部二值化二、Python局部二值化三、FPGA局部二值化总结 前言 局部二值化较全局二值化难,我们将在此实现Python与FPGA的局部二值化处理。 一、局部二值化 局部二值化就是使用一个窗口,在图像上进行扫描,每扫出9个像素求平均…...

shell文本处理工具-shell三剑客1
shell脚本常用基础命令2 shell脚本常用基础命令 shell脚本常用基础命令2一、grep用法二、sed用法2.1p参数 (显示)n参数(只显示处理过的行) 文本处理三剑客:grep sed awk 一、grep用法 grep -E egrep (扩展搜索正文表…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
