【智能算法】蜻蜓算法(DA)原理及实现

目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.代码实现
- 4.参考文献
1.背景
2016年,Mirjalili受到蜻蜓静态和动态集群行为启发,提出了蜻蜓算法(Dragonfly algorithm, DA)。
2.算法原理
2.1算法思想
蜻蜓集群有两种行为目的:狩猎(静态集群)和迁徙(动态集群)。静态集群中,蜻蜓分成小群捕猎,局部移动和突然飞行路径变化是其特征。动态集群则是大量蜻蜓在单一方向上长距离迁徙。这两种行为类似于元启发式优化中的探索和开发利用阶段,静态集群探索不同区域,而动态集群利用大群体沿着一个方向飞行。
2.2算法过程
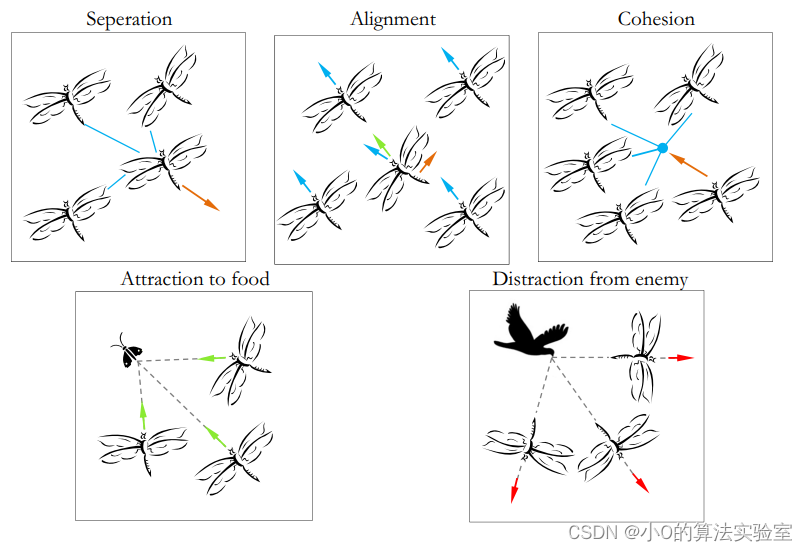
群体的行为遵循三个基本原则:
- 分离(Separation):指个体在邻域内静态地避免与其他个体碰撞
- 对齐(Alignment):表示个体的速度与邻域内其他个体的速度匹配
- 凝聚(Cohesion):指个体朝向邻域质心的趋势
分离:
S i = − ∑ j = 1 N X i − X j S_i=-\sum_{j=1}^NX_i-X_j Si=−j=1∑NXi−Xj
其中, X j X_j Xj表示第 i i i只蜻蜓领域内其他蜻蜓, S i S_i Si表示第 i i i只蜻蜓分离位置向量。
对齐:
A i = ∑ j = 1 N V j N A_{i}=\frac{\sum_{j=1}^{N}V_{j}}{N} Ai=N∑j=1NVj
其中, A i A_i Ai表示第 i i i只蜻蜓与领域内其他蜻蜓对齐的位置向量。
凝聚:
C i = ∑ j = 1 N X j N − X i C_i=\frac{\sum_{j=1}^NX_j}N-X_i Ci=N∑j=1NXj−Xi
其中, C i C_i Ci示第 i i i只蜻蜓凝聚时的位置向量。
寻找食物:
F i = X + − X i F_i=X^+-X_i Fi=X+−Xi
其中, X + X^+ X+表示猎物位置。
躲避天敌:
E i = X − + X i E_i=X^-+X_i Ei=X−+Xi
其中, X − X^- X−表示天敌位置。
位置更新:
Δ X t + 1 = ( s S i + a A i + c C i + f F i + e E i ) + w Δ X t X t + 1 = X t + Δ X t + 1 \Delta X_{t+1}=(sS_i+aA_i+cC_i+fF_i+eE_i)+w\Delta X_t \\ X_{t+1}=X_t+\Delta X_{t+1} ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+wΔXtXt+1=Xt+ΔXt+1
式中参数均为权重因子。
为了提高DA随机性和探索能力,当没有邻近解时,它们需要在搜索空间中进行Lévy飞行:
X t + 1 = X t + L e ˊ vy ( d ) × X t X_{t+1}=X_t+\text{Lévy}(d)\times X_t Xt+1=Xt+Leˊvy(d)×Xt
Lévy函数表述如下(Mantegna算法):
L e ˊ vy ( x ) = 0.01 × r 1 × σ ∣ r 2 ∣ 1 β σ = ( Γ ( 1 + β ) × sin ( π β 2 ) Γ ( 1 + β 2 ) × β × 2 ( β − 1 2 ) ) 1 / β \text{Lévy}(x)=0.01\times\frac{r_1\times\sigma}{|r_2|^{\frac1\beta}} \\ \sigma=\left(\frac{\Gamma(1+\beta)\times\sin\left(\frac{\pi\beta}{2}\right)}{\Gamma\left(\frac{1+\beta}{2}\right)\times\beta\times2^{\left(\frac{\beta-1}{2}\right)}}\right)^{1/\beta} Leˊvy(x)=0.01×∣r2∣β1r1×σσ= Γ(21+β)×β×2(2β−1)Γ(1+β)×sin(2πβ) 1/β
伪代码:

3.代码实现
% 蜻蜓优化算法
function [Best_pos,Best_fitness,Iter_curve,History_pos, History_best]=DA(pop, dim, ub,lb, fobj, maxIter)
%input
%pop 种群数量
%dim 问题维数
%ub 变量上边界
%lb 变量下边界
%fobj 适应度函数
%maxIter 最大迭代次数
%output
%Best_pos 最优位置
%Best_fitness 最优适应度值
%Iter_curve 每代最优适应度值
%History_pos 每代种群位置
%History_best 每代最优个体位置
%% 记录
Iter_curve=zeros(1,maxIter);
r=(ub-lb)/10;
Delta_max=(ub-lb)/10;
Food_fitness=inf;
Food_pos=zeros(dim,1);
Enemy_fitness=-inf;
Enemy_pos=zeros(dim,1);
%% 初始化
X=initialization(pop,dim,ub,lb);
Fitness=zeros(1,pop);
DeltaX=initialization(pop,dim,ub,lb);
%% 迭代
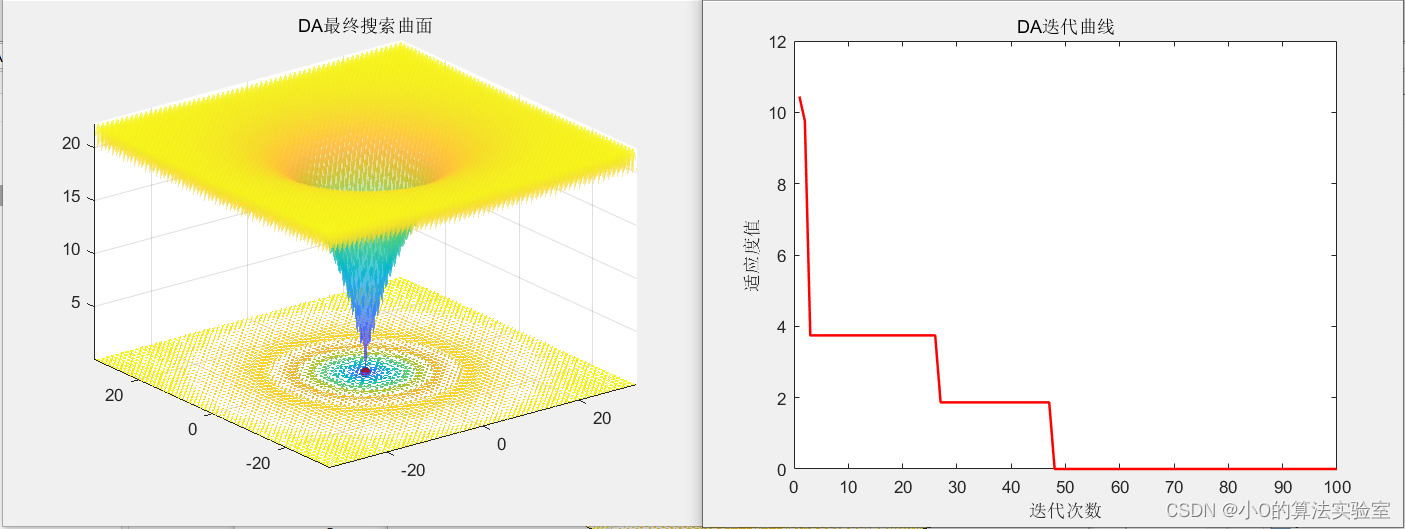
for iter=1:maxIterr=(ub-lb)/4+((ub-lb)*(iter/maxIter)*2);w=0.9-iter*((0.9-0.4)/maxIter);my_c=0.1-iter*((0.1-0)/(maxIter/2));if my_c<0my_c=0;ends=2*rand*my_c; % Seperation weighta=2*rand*my_c; % Alignment weightc=2*rand*my_c; % Cohesion weightf=2*rand; % Food attraction weighte=my_c; % Enemy distraction weightfor i=1:pop %Calculate all the objective values firstFitness(1,i)=fobj(X(:,i)');if Fitness(1,i)<Food_fitnessFood_fitness=Fitness(1,i);Food_pos=X(:,i);endif Fitness(1,i)>Enemy_fitnessif all(X(:,i)<ub') && all( X(:,i)>lb')Enemy_fitness=Fitness(1,i);Enemy_pos=X(:,i);endendendfor i=1:popindex=0;neighbours_no=0;clear Neighbours_DeltaXclear Neighbours_Xfor j=1:popDist2Enemy=distance(X(:,i),X(:,j));if (all(Dist2Enemy<=r) && all(Dist2Enemy~=0))index=index+1;neighbours_no=neighbours_no+1;Neighbours_DeltaX(:,index)=DeltaX(:,j);Neighbours_X(:,index)=X(:,j);endend% 分离% Eq. (3.1)S=zeros(dim,1);if neighbours_no>1for k=1:neighbours_noS=S+(Neighbours_X(:,k)-X(:,i));endS=-S;elseS=zeros(dim,1);end% 对齐% Eq. (3.2)if neighbours_no>1A=(sum(Neighbours_DeltaX')')/neighbours_no;elseA=DeltaX(:,i);end% 凝聚% Eq. (3.3)if neighbours_no>1C_temp=(sum(Neighbours_X')')/neighbours_no;elseC_temp=X(:,i);endC=C_temp-X(:,i);% 寻找食物% Eq. (3.4)Dist2Food=distance(X(:,i),Food_pos(:,1));if all(Dist2Food<=r)F=Food_pos-X(:,i);elseF=0;end% 躲避天敌% Eq. (3.5)Dist2Enemy=distance(X(:,i),Enemy_pos(:,1));if all(Dist2Enemy<=r)Enemy=Enemy_pos+X(:,i);elseEnemy=zeros(dim,1);endfor tt=1:dimif X(tt,i)>ub(tt)X(tt,i)=lb(tt);DeltaX(tt,i)=rand;endif X(tt,i)<lb(tt)X(tt,i)=ub(tt);DeltaX(tt,i)=rand;endendif any(Dist2Food>r)if neighbours_no>1for j=1:dimDeltaX(j,i)=w*DeltaX(j,i)+rand*A(j,1)+rand*C(j,1)+rand*S(j,1);if DeltaX(j,i)>Delta_max(j)DeltaX(j,i)=Delta_max(j);endif DeltaX(j,i)<-Delta_max(j)DeltaX(j,i)=-Delta_max(j);endX(j,i)=X(j,i)+DeltaX(j,i);endelse% Eq. (3.8)X(:,i)=X(:,i)+Levy(dim)'.*X(:,i);DeltaX(:,i)=0;endelsefor j=1:dim% Eq. (3.6)DeltaX(j,i)=(a*A(j,1)+c*C(j,1)+s*S(j,1)+f*F(j,1)+e*Enemy(j,1)) + w*DeltaX(j,i);if DeltaX(j,i)>Delta_max(j)DeltaX(j,i)=Delta_max(j);endif DeltaX(j,i)<-Delta_max(j)DeltaX(j,i)=-Delta_max(j);endX(j,i)=X(j,i)+DeltaX(j,i);end endFlag4ub=X(:,i)>ub';Flag4lb=X(:,i)<lb';X(:,i)=(X(:,i).*(~(Flag4ub+Flag4lb)))+ub'.*Flag4ub+lb'.*Flag4lb;endBest_fitness=Food_fitness;Best_pos=Food_pos;Iter_curve(iter)=Best_fitness;History_pos{iter} = X;History_best{iter} = Best_pos;
end
end
%% 欧式距离
function o = distance(a,b)for i=1:size(a,1)o(1,i)=sqrt((a(i)-b(i))^2);
end
end
%% 位置初始化
function Positions=initialization(SearchAgents_no,dim,ub,lb)Boundary_no= size(ub,2); if Boundary_no==1ub_new=ones(1,dim)*ub;lb_new=ones(1,dim)*lb;
elseub_new=ub;lb_new=lb;
end
for i=1:dimub_i=ub_new(i);lb_i=lb_new(i);Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
endPositions=Positions';
end
%% Levy飞行
function o=Levy(d)beta=3/2;
%Eq. (3.10)
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;
v=randn(1,d);
step=u./abs(v).^(1/beta);% Eq. (3.9)
o=0.01*step;
end
4.参考文献
[1] Mirjalili S. Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems[J]. Neural computing and applications, 2016, 27: 1053-1073.
[2] Mantegna RN. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic process. Phys Rev E 1994;49(5):4677–83.
相关文章:

【智能算法】蜻蜓算法(DA)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.代码实现4.参考文献 1.背景 2016年,Mirjalili受到蜻蜓静态和动态集群行为启发,提出了蜻蜓算法(Dragonfly algorithm, DA)。 2.算法原理 2.1算法思想 蜻蜓集群有两种行为目的:狩猎…...

用A*算法求解八数码问题
用A*算法求解八数码问题 实现两种启发函数实现A*算法测试 实现两种启发函数 采取两种策略实现启发函数: 策略1:不在目标位置的数字个数策略2:曼哈顿距离(将数字直接移动到对应位置的步数总数) # 策略1: 不在目标位置…...
分布式之Ribbon使用以及原理
Ribbon使用以及原理 1、负载均衡的两种方式 服务器端负载均衡 传统的方式前端发送请求会到我们的的nginx上去,nginx作为反向代理,然后路由给后端的服务器,由于负载均衡算法是nginx提供的,而nginx是部署到服务器端的,所…...

android JNI float *转MutableList
data class Test(var data:MutableList<Float> )JNIEXPORT void JNICALL Java_NativeUtils_assignFloatArrayToHealth(JNIEnv *env, jclass clazz, jobject obj, jfloatArray cData) {jclass objClass env->GetObjectClass(obj);// 获取 Test类中的 data 属性jfieldI…...

chatgpt与人类有何不同?
ChatGPT和人类之间存在多个显著的差异。 首先,ChatGPT是一种基于人工智能技术的计算机程序,通过机器学习和自然语言处理等技术,从大量的数据中获取知识并生成语言输出。它主要依赖于算法和数据进行工作,能够迅速处理和检索信息&a…...
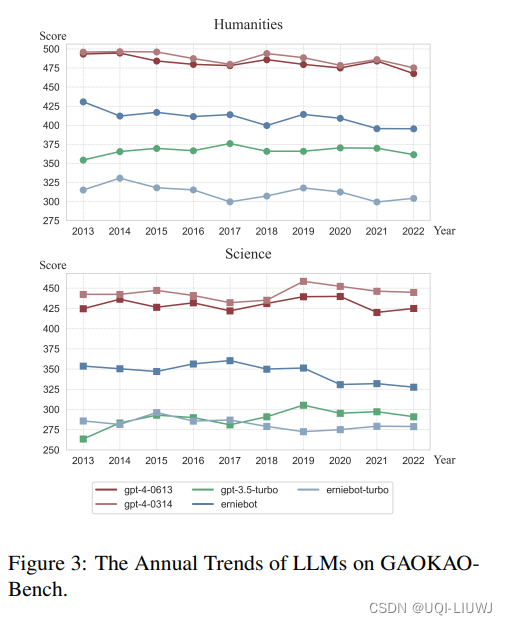
论文笔记:Evaluating the Performance of Large Language Models on GAOKAO Benchmark
1 论文思路 采用zero-shot prompting的方式,将试题转化为ChatGPT的输入 对于数学题,将公式转化为latex输入 主观题由专业教师打分 2 数据 2010~2022年,一共13年间的全国A卷和全国B卷 3 结论 3.1 不同模型的zeroshot 高考总分 3.2 各科主…...

MySQL 数据库查询与数据操作:使用 ORDER BY 排序和 DELETE 删除记录
使用 ORDER BY 进行排序 使用 ORDER BY 语句按升序或降序对结果进行排序。 ORDER BY 关键字默认按升序排序。要按降序排序结果,使用 DESC 关键字。 示例按名称按字母顺序排序结果: import mysql.connectormydb mysql.connector.connect(host"l…...

数据结构入门(3)2.链表接口实现
目录 前言 头文件 动态申请一个结点 单链表打印 单链表尾插 单链表的头插 单链表的尾删 单链表头删 单链表查找 单链表在pos位置之后插入x 单链表删除pos位置之后的值 在pos的前面插入 删除pos位置 销毁顺序表 前言 本文将介绍链表常见的功能的实现 头文件 #…...
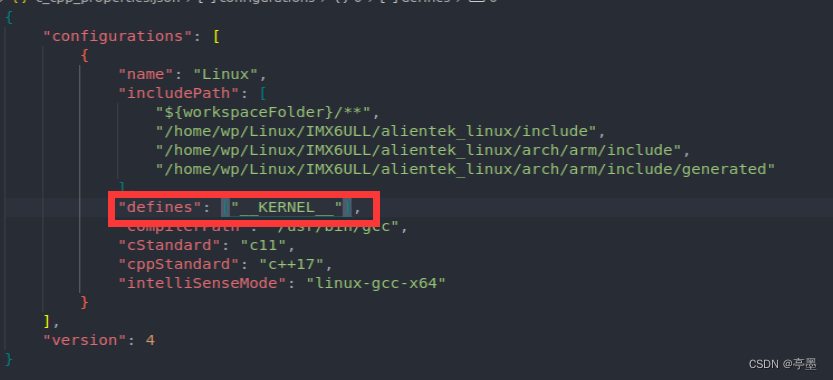
vscode中解决驱动编写的时候static int __init chrdev_init()报错的问题
目录 错误出错原因解决方法 错误 在入口函数上,出现 expected a ; 这样的提示 出错原因 缺少了 __KERNEL __ 宏定义 解决方法 补上__KERNEL__宏定义 具体做法:在vscode中按下ctrlshiftp ,输入:C/C:Edit Configurations࿰…...

fastgpt本地详细部署以及配置
目录 一、Docker部署1、docker安装2、docker启动3、添加用户到 docker 组:4、验证 Docker 安装:二、one_api 本地部署1、linux系统部署2、windows系统部署三、向量模型部署(m3e)四、chatglm2模型本地部署五、fastgpt模型本地部署1、下载配置文件2、文件配置--docker-compos…...

【故障分类】基于注意力机制的卷积神经网络结合双向长短记忆神经网络CNN-BiLSTM-attention实现数据分类附matlab代码
摘要: ntion机制加权 4. 加权后的特征进行分类 需求分析 本文旨在实现一个通用的数据分类模型,可应用于不同领域的数据分类任务。 设计方案 设计一个CNN网络结构,提取输入数据的特征 将特征序列输入到BiLSTM网络,进行时序建模…...
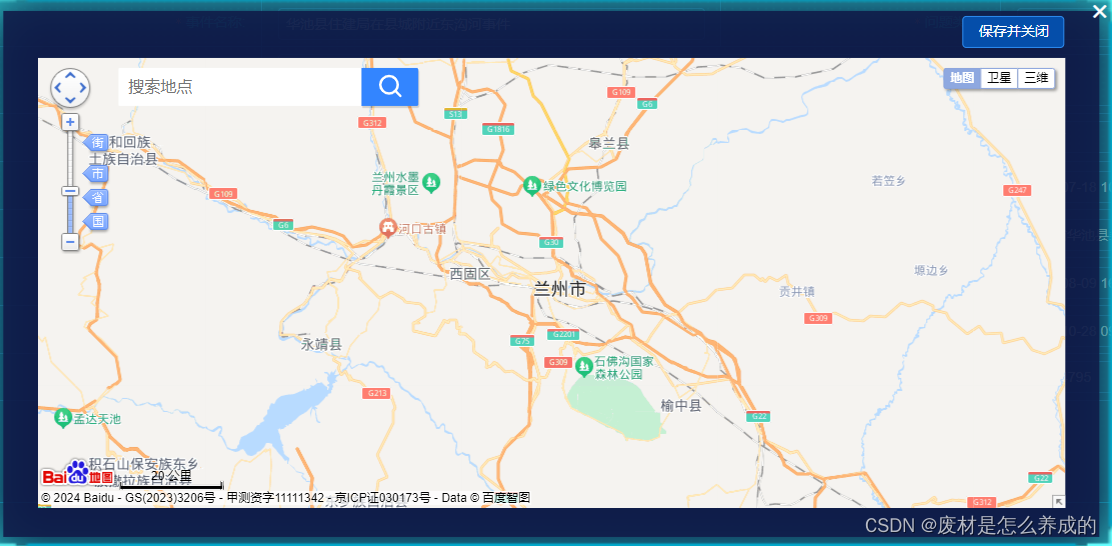
vue接入百度地图获取经纬度
通过城市名称和城市中心经纬度来获取当前所在地图,当前经纬度中心获取可以通过后端获取 静态文件包,替换baidu.html中的ak值,ak值通过百度地图官方网站申请 申请:百度地图API申请步骤 - 知乎 代码示例文件: 链接&a…...

交流负载箱的特点和优势有哪些?
交流负载箱广泛应用于电力系统、新能源、轨道交通、航空航天等领域。它具有以下特点和优势: 1. 灵活性高:交流负载箱可以根据实际需求,调整输出电流、电压、功率等参数,以满足不同场景下的测试需求。同时,它还可以实现…...

Java线程锁之Lock的使用
Lock 的使用 Lock 是java 1.5 中引入的线程同步工具,它主要用于多线程下共享资源的控制。本质上Lock 仅仅是一个接口, 可以通过显式定义同步锁对象来实现同步,能够提供比synchronized 更广泛的锁定操作,并支持多个相关的 Lock接…...
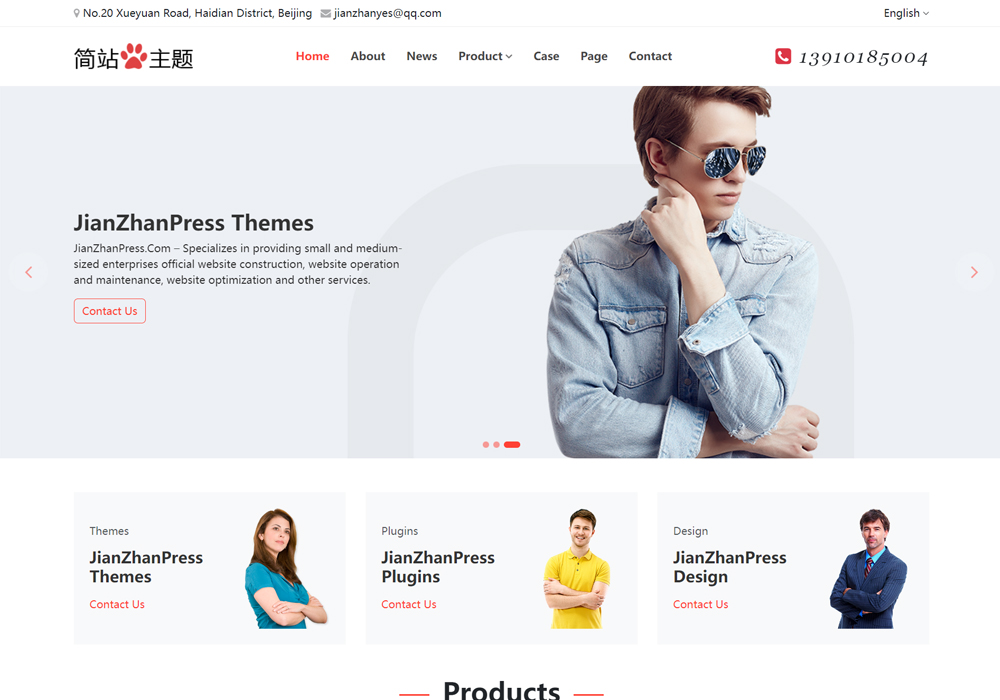
简站wordpress主题看上去差不多 实际大不一样
有人说简站wordpress主题,都差不多嘛。我表示无语。表面看上去是差不多的,实际的细节是不一样的。 下面以编号:JZP4431和编号:JZP4878这两个主题为例子来讲一下,简站wordpress主题,在细节方面的不一样之处…...
(完美方案)解决mfc140u.dll文件丢失问题,快速且有效的修复
唉,又是丢失了mfc140u.dll,这该怎么办呢?如果你的电脑突然找不到或丢失mfc140u.dll文件,那就真是太糟糕了。别担心,我分享给你一些干货,告诉你如何快速解决mfc140u.dll丢失的问题。 一.mfc140u.dll属性功能…...

并发通信(网络进程线程)
如果为每个客户端创建一个进程(或线程),因为linux系统文件标识符最多1024位,是有限的。 所以使用IO复用技术,提高并发程度。 阻塞与非阻塞 阻塞式复用 非阻塞复用 信号驱动IO 在属主进程(线程中声明&…...

WPF 该线程是用不接受参数的 ThreadStart 委托创建的。
创建无参数线程是无法发去传递参数的,需要把 《 thread.Start(“张三”); 》改为《 thread.Start(); 》 把参数去掉就可以了。 public RegisterWindow(){InitializeComponent();//无参数线程Thread thread new Thread(pageLoad);thread.IsBackground true;//thr…...

FreeRTOS学习第9篇--队列介绍
目录 FreeRTOS学习第9篇--队列介绍1. 数据传输的方法1.1 任务之间如何传输数据1.2 队列的本质 2. 队列的工作原理和实现2.1 创建队列2.2 向队列发送数据2.3 从队列接收数据 3. 使用队列进行任务间的通信3.1 通信示例3.2 同步示例 结论 FreeRTOS学习第9篇–队列介绍 本文目标&a…...

qt如何配置ros环境
在Qt5.7的版本可以使用bash -i -c来启动qt,让Qt自己识别系统环境,不知道为什么Qt在之后的版本,这样使用都失效了。因为它会默认把CMAKE_PREFIX_PATH修改掉。 网上还有安装ros插件版本的qt creator,感觉失去了一些灵活性。 自己测试…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
