【机器学习】Linear and Nonlinear Regression 线性/非线性回归讲解
文章目录
- 一、回归问题概述
- 二、误差项定义
- 三、独立同分布的假设
- 四、似然函数的作用
- 五、参数求解
- 六、梯度下降算法
- 七、参数更新方法
- 八、优化参数设置
一、回归问题概述
回归:根据工资和年龄,预测额度为多少
其中,工资和年龄被称为特征(自变量),额度被称为标签(因变量)

下图展示了线性回归特性,其相当于Y = aX1+bX2+c,在此问题中,就相当于一个三维空间中的二维平>面,我们希望找到一个二维平面,尽可能接近所有点
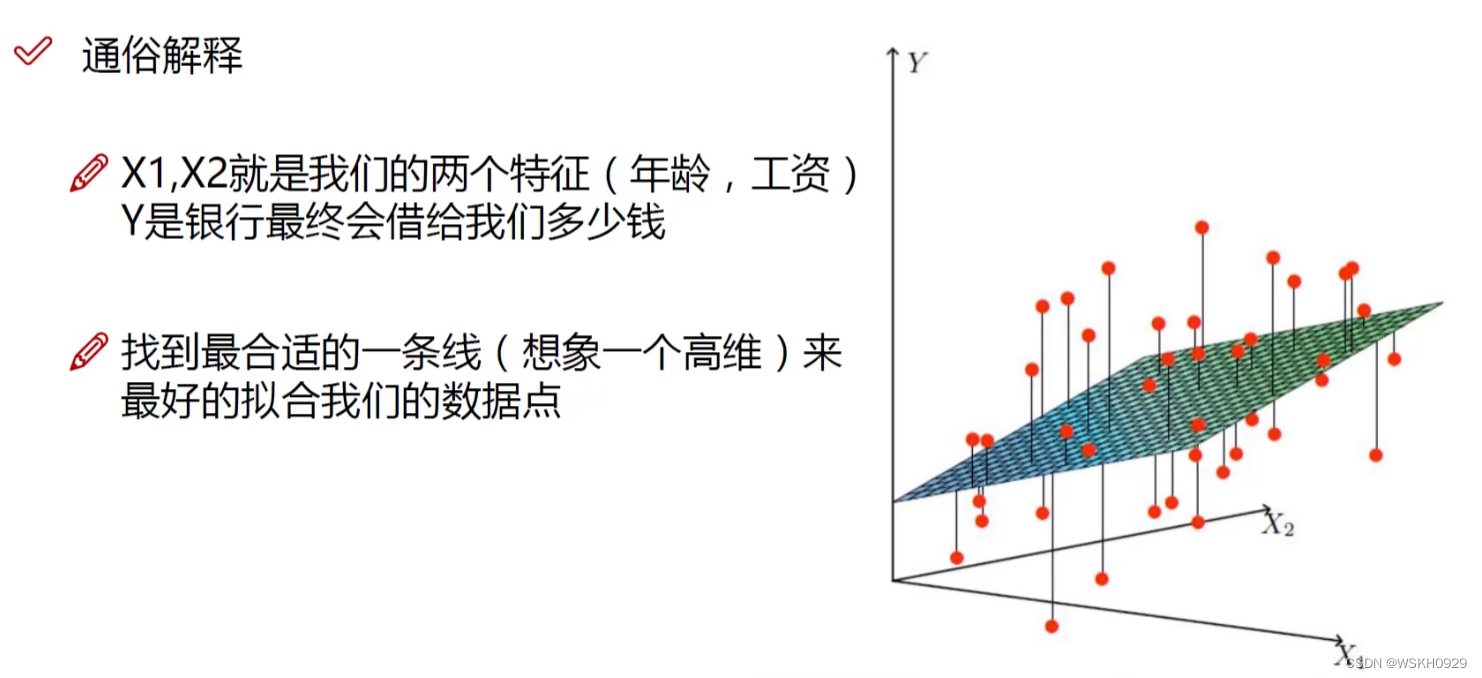
二、误差项定义
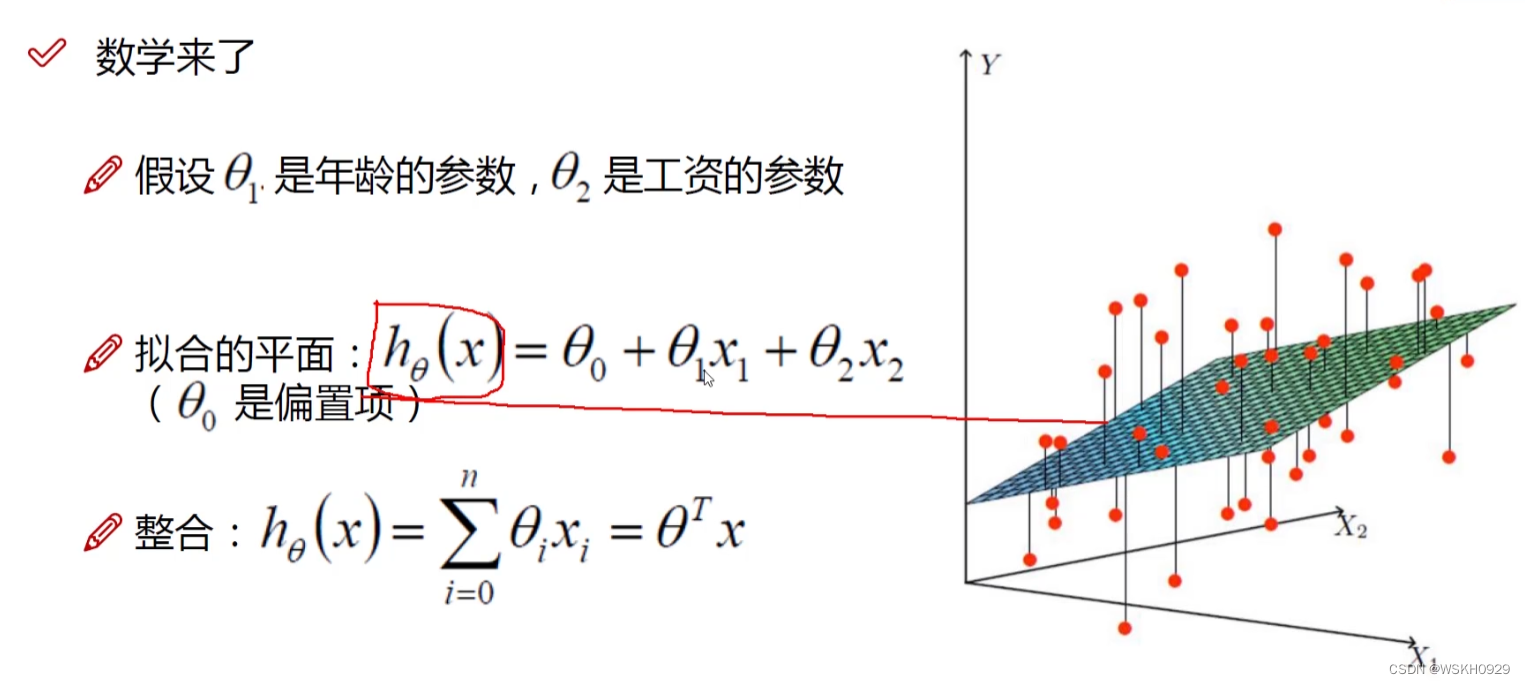
下图展示了误差项的定义,我们一般认为误差项越接近0越好
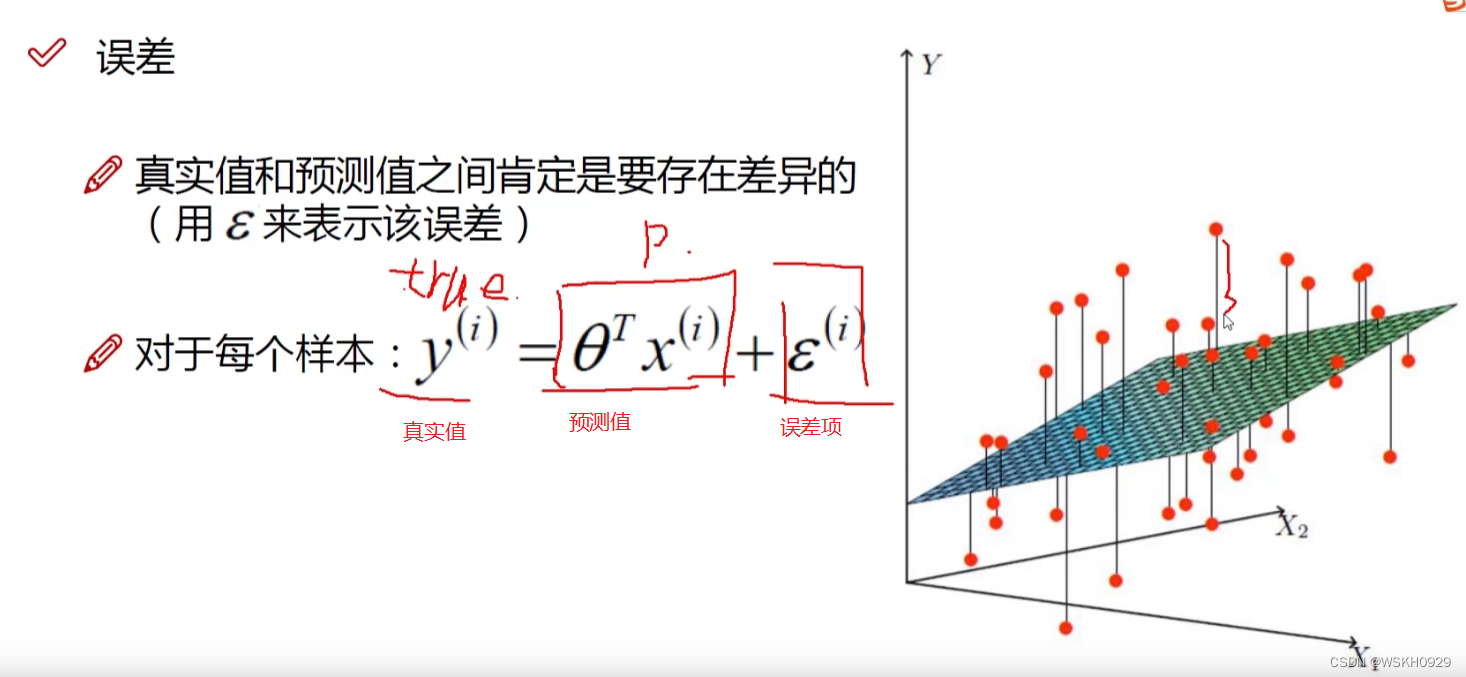
三、独立同分布的假设
- 误差 ε(i)\varepsilon^{(i)}ε(i) 是独立并且具有相同的分布, 并且服从均值为0方差为 θ2\boldsymbol{\theta}^2θ2 的高斯分布
- 独立:张三和李四一起来贷款,他俩没关系
- 同分布: 他俩都来得是我们假定的这家银行
- 高斯分布(正态分布) : 银行可能会多给,也可能会少给,但是绝大多数情况下 这个浮动不会太大,极小情况下浮动会比较大,符合正常情况

四、似然函数的作用
(1) 预测值与误差 :
y(i)=θTx(i)+ε(i)y^{(i)}=\theta^T x^{(i)}+\varepsilon^{(i)}y(i)=θTx(i)+ε(i)
(2) 由于误差服从高斯分布 :
p(ϵ(i))=12πσexp(−(ϵ(i))22σ2)p\left(\epsilon^{(i)}\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(\epsilon^{(i)}\right)^2}{2 \sigma^2}\right)p(ϵ(i))=2πσ1exp(−2σ2(ϵ(i))2)
将 (1)(1)(1) 式带入 (2)(2)(2) 式:
p(y(i)∣x(i);θ)=12πσexp(−(y(i)−θTx(i))22σ2)p\left(y^{(i)} \mid x^{(i)} ; \theta\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^T x^{(i)}\right)^2}{2 \sigma^2}\right)p(y(i)∣x(i);θ)=2πσ1exp(−2σ2(y(i)−θTx(i))2)
似然函数(独立同分布的前提下,联合概率密度等于边缘概率密度的乘积) :
L(θ)=∏i=1mp(y(i)∣x(i);θ)=∏i=1m12πσexp(−(y(i)−θTx(i))22σ2)L(\theta)=\prod_{i=1}^m p\left(y^{(i)} \mid x^{(i)} ; \theta\right)=\prod_{i=1}^m \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^T x^{(i)}\right)^2}{2 \sigma^2}\right)L(θ)=i=1∏mp(y(i)∣x(i);θ)=i=1∏m2πσ1exp(−2σ2(y(i)−θTx(i))2)
解释 : 什么样的参数跟我们的数据组合后恰好是真实值
对数似然 :
logL(θ)=log∏i=1m12πσexp(−(y(i)−θTx(i))22σ2)\log L(\theta)=\log \prod_{i=1}^m \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^T x^{(i)}\right)^2}{2 \sigma^2}\right)logL(θ)=logi=1∏m2πσ1exp(−2σ2(y(i)−θTx(i))2)
解释 : 乘法难解,加法就容易了,对数里面乘法可以转换成加法
五、参数求解
展开化简 :
∑i=1mlog12πσexp(−(y(i)−θTx(i))22σ2)=mlog12πσ−1σ2⋅12∑i=1m(y(i)−θTx(i))2\sum_{i=1}^m \log \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^T x^{(i)}\right)^2}{2 \sigma^2}\right) \\ =m \log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{i=1}^m\left(y^{(i)}-\theta^T x^{(i)}\right)^2 i=1∑mlog2πσ1exp(−2σ2(y(i)−θTx(i))2)=mlog2πσ1−σ21⋅21i=1∑m(y(i)−θTx(i))2
目标:让似然函数(对数变换后也一样 ) 越大越好
J(θ)=12∑i=1m(y(i)−θTx(i))2( 最小二乘法 ) J(\theta)=\frac{1}{2} \sum_{i=1}^m\left(y^{(i)}-\theta^T x^{(i)}\right)^2 \text { ( 最小二乘法 ) } J(θ)=21i=1∑m(y(i)−θTx(i))2 ( 最小二乘法 )
目标函数 :
J(θ)=12∑i=1m(hθ(x(i))−y(i))2=12(Xθ−y)T(Xθ−y)J(\theta)=\frac{1}{2} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2=\frac{1}{2}(X \theta-y)^T(X \theta-y)J(θ)=21i=1∑m(hθ(x(i))−y(i))2=21(Xθ−y)T(Xθ−y)
求偏导:
∇θJ(θ)=∇θ(12(Xθ−y)T(Xθ−y))=∇θ(12(θTXT−yT)(Xθ−y))=∇θ(12(θTXTXθ−θTXTy−yTXθ+yTy))=12(2XTXθ−XTy−(yTX)T)=XTXθ−XTy\begin{aligned} \quad \nabla_\theta J(\theta)&=\nabla_\theta\left(\frac{1}{2}(X \theta-y)^T(X \theta-y)\right) \\ &=\nabla_\theta\left(\frac{1}{2}\left(\theta^T X^T-y^T\right)(X \theta-y)\right) \\ &=\nabla_\theta\left(\frac{1}{2}\left(\theta^T X^T X \theta-\theta^T X^T y-y^T X \theta+y^T y\right)\right) \\ &=\frac{1}{2}\left(2 X^T X \theta-X^T y-\left(y^T X\right)^T\right)=X^T X \theta-X^T y \end{aligned} ∇θJ(θ)=∇θ(21(Xθ−y)T(Xθ−y))=∇θ(21(θTXT−yT)(Xθ−y))=∇θ(21(θTXTXθ−θTXTy−yTXθ+yTy))=21(2XTXθ−XTy−(yTX)T)=XTXθ−XTy
偏导等于0:
θ=(XTX)−1XTy\theta=\left(X^T X\right)^{-1} X^T yθ=(XTX)−1XTy
六、梯度下降算法
引入: 当我们得到了一个目标函数后,如何进行求解?
直接求解 ? ( 并不一定可解,线性回归可以当做是一个特例 )
常规套路: 机器学习的套路就是我交给机器一堆数据, 然后告诉它 什么样的学习方式是对的(目标函数),然后让它朝着这个方向去做
如何优化: 一口吃不成个胖子,我们要静悄悄的一步步的完成迭代 ( 每次优化一点点,累积起来就是个大成绩了)

七、参数更新方法
目标函数 :
J(θ0,θ1)=12m∑i=1m(hθ(x(i))−y(i))2J\left(\theta_0, \theta_1\right)=\frac{1}{2 m} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
寻找山谷的最低点,也就是我们的目标函数终点 ( 什么样的参数能使得目标函数达到极值点)
下山分几步走呢? ( 更新参数 )
(1) : 找到当前最合适的方向
(2) : 走那么一小步,走快了该" 跌倒 "了
(3):按照方向与步伐去更新我们的参数
批量梯度下降:
∂J(θ)∂θj=−1m∑i=1m(yi−hθ(xi))xjiθj′=θj+1m∑i=1m(yi−hθ(xi))xji\frac{\partial J(\theta)}{\partial \theta_j}=-\frac{1}{m} \sum_{i=1}^m\left(y^i-h_\theta\left(x^i\right)\right) x_j^i \\ \theta_j^{\prime}=\theta_j+\frac{1}{m} \sum_{i=1}^m\left(y^i-h_\theta\left(x^i\right)\right) x_j^i∂θj∂J(θ)=−m1i=1∑m(yi−hθ(xi))xjiθj′=θj+m1i=1∑m(yi−hθ(xi))xji
( 容易得到最优解,但是由于每次考虑所有样本,速度很慢 )
随机梯度下降 :
θj′=θj+(yi−hθ(xi))xji\theta_j^{\prime}=\theta_j+\left(y^i-h_\theta\left(x^i\right)\right) x_j^iθj′=θj+(yi−hθ(xi))xji
(每次找一个样本,迭代速度快,但不一定每次都朝着收敛的方向 )
小批量梯度下降法 :
θj:=θj−α110∑k=ii+9(hθ(x(k))−y(k))xj(k)\theta_j:=\theta_j-\alpha \frac{1}{10} \sum_{k=i}^{i+9}\left(h_\theta\left(x^{(k)}\right)-y^{(k)}\right) x_j^{(k)}θj:=θj−α101k=i∑i+9(hθ(x(k))−y(k))xj(k)
(每次更新选择一小部分数据来算,实用!)
八、优化参数设置
学习率(步长):对结果产生巨大影响,一般小一些
如何选择: 从小的时候,不行再小
批处理数量 : 32,64,128 都可以,很多 时候还得考虑内存和效率

相关文章:

【机器学习】Linear and Nonlinear Regression 线性/非线性回归讲解
文章目录一、回归问题概述二、误差项定义三、独立同分布的假设四、似然函数的作用五、参数求解六、梯度下降算法七、参数更新方法八、优化参数设置一、回归问题概述 回归:根据工资和年龄,预测额度为多少 其中,工资和年龄被称为特征࿰…...
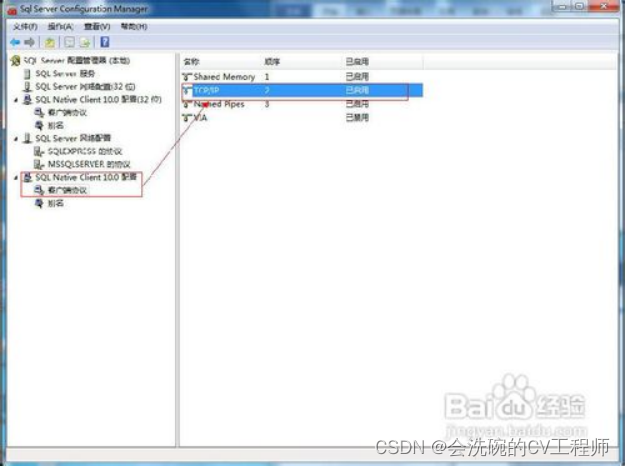
PyQt5数据库开发1 4.1 SQL Server 2008 R2如何开启数据库的远程连接
文章目录 前言 步骤/方法 1 使用windows身份登录 2 启用混合登录模式 3 允许远程连接服务器 4 设置sa用户属性 5 配置服务器 6 重新登录 7 配置SSCM 8 确认防火墙设置 注意事项 前言 SQL Server 2008 R2如何开启数据库的远程连接 SQL Server 2008默认是不允许远程连…...
javassm高校学生评教系统的设计与实现idea msyql
伴随着社会以及科学技术的发展,互联网已经渗透在人们的身边,网络慢慢的变成了人们的生活必不可少的一部分,紧接着网络飞速的发展,管理系统这一名词已不陌生,越来越多的学校、公司等机构都会定制一款属于自己个性化的管…...
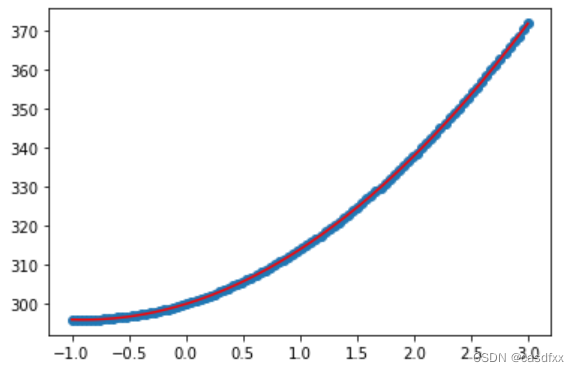
为什么神经网络做不了2次函数拟合,网上的都是骗人的吗?
环境:tensorflow2 kaggle 这几天突发奇想,用深度学习训练2次函数。先在网上找找相同的资料这方面资料太少了。大多数如下: 。 给我的感觉就是,用深度学习来做,真的很容易。 网上写出代码分析的比较少。但是也找到了…...
【Java】Help notes about JAVA
JAVA语言帮助笔记Java的安装与JDKJava命名规范JAVA的数据类型自动类型转换强制类型转换JAVA的运算符取余运算结果的符号逻辑运算的短路运算三元运算符运算符优先级JAVA的流程控制分支结构JAVA类Scanner类Java的安装与JDK JDK安装网站:https://www.oracle.com/java/…...

2023北京老博会,北京养老展,第十届中国国际老年产业博览会
2023第十届(北京)国际老年产业博览会,将于08月28-30日盛大举办; 2023北京老博会:2023第十届中国(北京)国际老年产业博览会The 2023 tenth China (Beijing) International Aged industry Expo&a…...
C++展开模板参数包、函数参数包-(lambda+折叠表达式)
开门见山 以下代码可展开模板参数包和展开函数参数包。 // lambda折叠表达式(需C17) #include <iostream> using namespace std;// 1.展开模板参数包 template<typename ...T> void Func1() {([]() {cout << typeid(T).name() << endl;}(), ...);// …...
【Spark分布式内存计算框架——Spark Core】7. RDD Checkpoint、外部数据源
第五章 RDD Checkpoint RDD 数据可以持久化,但是持久化/缓存可以把数据放在内存中,虽然是快速的,但是也是最不可靠的;也可以把数据放在磁盘上,也不是完全可靠的!例如磁盘会损坏等。 Checkpoint的产生就是…...

Connext DDSQoS参考
1 QoS策略列表 ConnextDDS 6.1.1版中所有QoS策略的高级视图。 1. QoS策略描述...
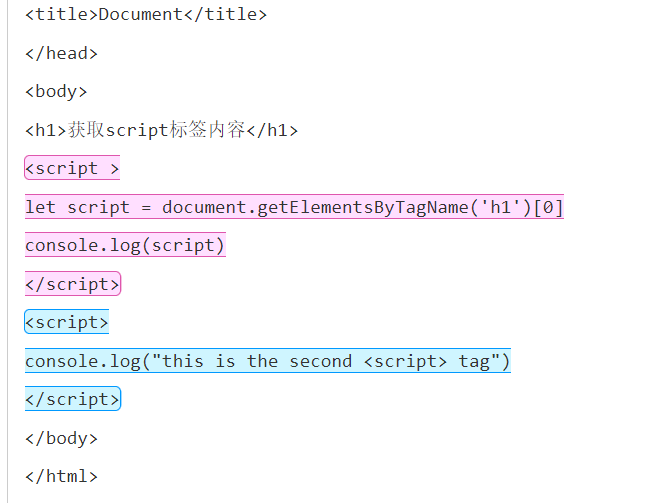
【正则表达式】获取html代码文本内所有<script>标签内容
文章目录一. 背景二. 思路与过程1. 正则表达式中需要限定<script>开头与结尾2. 增加标签格式的限定3. 不限制<script>首尾的内部内容4. 中间的内容不能出现闭合的情况三. 结果与代码四. 正则辅助工具一. 背景 之前要对学生提交的html代码进行检查,在获…...

有 9 种springMVC常用注解高频使用,来了解下?
文章目录1、Controller2、RequestMapping2.1 RequestMapping注解有六个属性2.1.1 value2.1.2 method2.1.3 consumes2.1.4 produces2.1.5 params2.1.6 headers2.2 Request Mapping("/helloword/?/aa")的Ant路径,匹配符2.3 Request …...

【ES6】掌握Promise和利用Promise封装ajax
💻 【ES6】掌握Promise和利用Promise封装ajax 🏠专栏:JavaScript 👀个人主页:繁星学编程🍁 🧑个人简介:一个不断提高自我的平凡人🚀 🔊分享方向:目…...
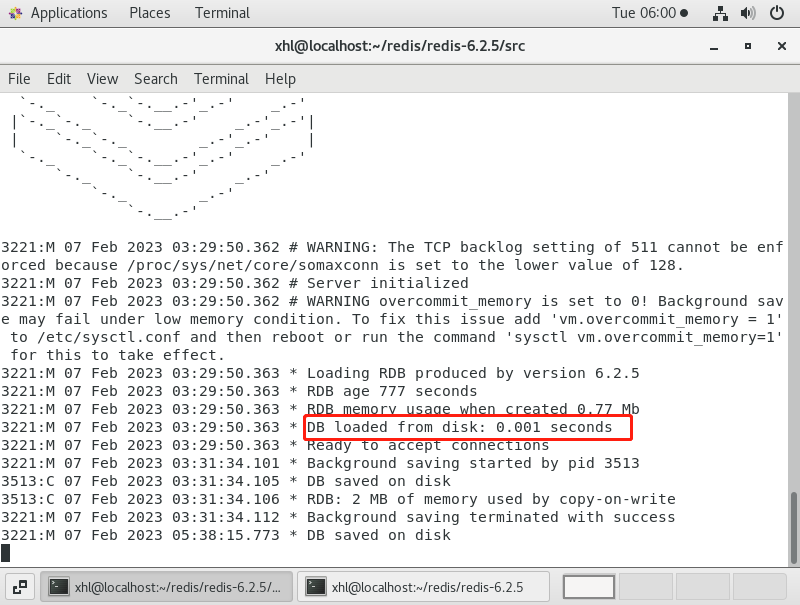
REDIS-持久化方案
我们知道redis是内存数据库,它的数据是存储在内存中的,我们知道内存的一个特点是断电数据就丢失,所以redis提供了持久化功能,可以将内存中的数据状态存储到磁盘里面,避免数据丢失。 Redis持久化有三种方案,…...
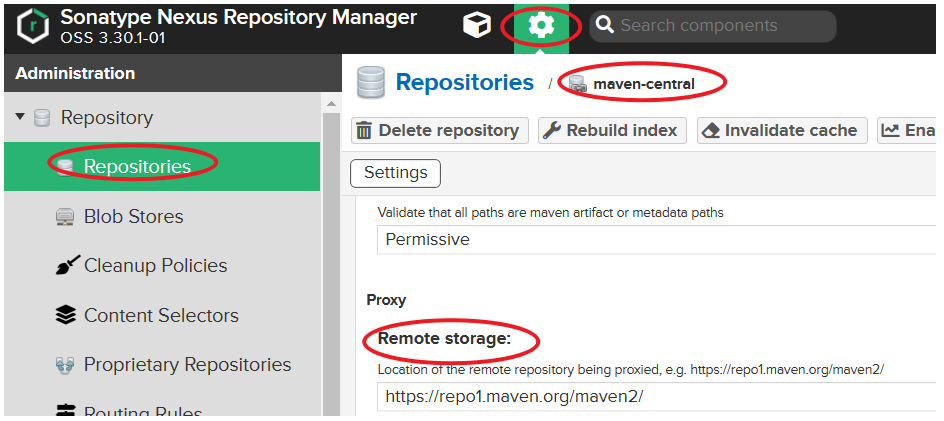
五、Java框架之Maven进阶
黑马课程 文章目录1. 分模块开发1.1 分模块开发入门案例示例:抽取domain层示例:抽取dao层1.2 依赖管理2. 聚合和继承2.1 聚合概述聚合实现步骤2.2 继承 dependencyManagement3. 属性管理3.1 依赖版本属性管理3.2 配置文件属性管理(了解&#…...

1.前言【Java面试第三季】
1.前言【Java面试第三季】前言推荐1.前言00_前言闲聊和课程说明本课程介绍目前考核的变化趋势vcr集数和坚持学长谷粉面试题复盘反馈最后前言 2023-2-1 12:30:05 以下内容源自 【尚硅谷Java大厂面试题第3季,跳槽必刷题目必扫技术盲点(周阳主讲࿰…...

06分支限界法
文章目录八数码难题普通BFS算法全局择优算法(A算法,启发式搜索算法)单源最短路径问题装载问题算法思想:队列式分支限界法优先队列式分支限界法布线问题最大团问题批处理作业调度问题分支限界法与回溯法的区别: &#x…...

Docker Compose编排
一、概念1、Docker Compose是什么Docker Compose的前身是Fig,它是一个定义及运行多个Docker容器的工具通过 Compose,不需要使用shell脚本来启动容器,而使用 YAML 文件来配置应用程序需要的所有服务然后使用一个命令,根据 YAML 的文…...

Docker进阶 - 11. Docker Compose 编排服务
注:本文只对一些重要步骤和yml文件进行一些讲解,其他的具体程序没有记录。 目录 1. 原始的微服务工程编排(不使用Compose) 2. 使用Compose编排微服务 2.1 编写 docker-compose.yml 文件 2.2 修改并构建微服务工程镜像 2.3 启动 docker-compose 服务…...
)
福利篇2——嵌入式岗位笔试面试资料汇总(含大厂笔试面试真题)
前言 汇总嵌入式软件岗位笔试面试资料,供参考。 文章目录 前言一、公司嵌入式面经1、小米1)面试时长2)面试问题2、科大讯飞1)面试时长2)面试题目3、其余公司面经二、嵌入式笔试面试资料(全)三、嵌入式岗位薪资报告四、硬件岗位薪资报告一、公司嵌入式面经 1、小米 1)…...

[ubuntu]LVM磁盘管理
LVM是 Logical Volume Manager(逻辑卷管理)的简写,是Linux环境下对磁盘分区进行管理的一种机制,由Heinz Mauelshagen在Linux 2.4内核上实现。LVM可以实现用户在无需停机的情况下动态调整各个分区大小。1.简介 LVM本质上是一个…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
