SNR = 6.02N + 1.76dB 公式推导
简介
接触ADC或DAC时您一定会碰到这个经常被引用的公式,用于计算转换器理论信噪比 (SNR)。与其盲目地相信表象,不如从根本上了解其来源,因为该公式蕴含着一些微妙之 处,如果不深入探究,可能导致对数据手册技术规格和转换器性能的误解。记住,该公式 代表的是完美N位ADC的理论性能。您可以比较ADC的实际SNR与理论SNR,看看二者有 何异同。 本教程首先推导N位模数转换器(ADC)的理论量化噪声,知道均方根量化噪声电压后,就 可以计算理论信噪比(SNR)。此外还会分析过采样对SNR的影响。
量化噪声模型
理想转换器对信号进行数字化时,最大误差为±½ LSB,如图1的一个理想N位ADC的传递 函数所示。对于任何横跨数个LSB的交流信号,其量化误差可以通过一个峰峰值幅度为q (一个LSB的权重)的非相关锯齿波形来近似计算。对该近似法还可以从另一个角度来看 待,即实际量化误差发生在±½ q范围内任意一点的概率相等。虽然这种分析不是百分之百 精确,但对大多数应用是足够准确的。
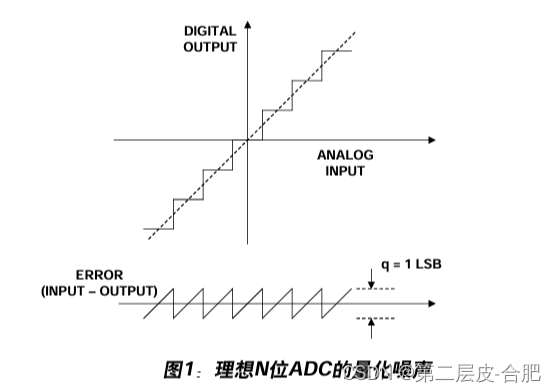
图2更详细地显示了量化误差与时间的关系。同样,一个简单的锯齿波形就能提供足够准 确的分析模型。锯齿误差的计算公式如下:
e(t) = st, –q/2s < t < +q/2s.
e(t)的均方值可以表示为:、
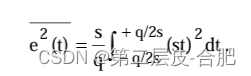
锯齿误差波形产生的谐波远远超过DC至fs /2的奈奎斯特带宽,然而,所有这些高阶谐波必 须折回(混叠)到奈奎斯特带宽并相加,产生q/√12的均方根噪声。 正如Bennett所指出的(参考文献1),量化噪声近似于高斯分布,几乎均匀地分布于从DC至 fs /2的奈奎斯特带宽。这里假设量化噪声与输入信号不相关。在某些条件下,当采样时钟和信号通过谐波相关时,量化噪声将与输入信号相关,能量集中在信号的谐波中,但均方 根值仍然约为q/√12。理论信噪比现在可以通过一个满量程输入正弦波来计算:
理想N位转换器的均方根信噪比为
 Bennett论文说明:虽然量化噪声的实际频谱相当复杂,难以分析,但推导出等式9的简化 分析对大多数应用足够准确。然而,必须再次强调,均方根量化噪声是在DC至fs/2的完整 奈奎斯特带宽范围内进行测量。
Bennett论文说明:虽然量化噪声的实际频谱相当复杂,难以分析,但推导出等式9的简化 分析对大多数应用足够准确。然而,必须再次强调,均方根量化噪声是在DC至fs/2的完整 奈奎斯特带宽范围内进行测量。
量化噪声与输入信号之间的相关性容易令人误解
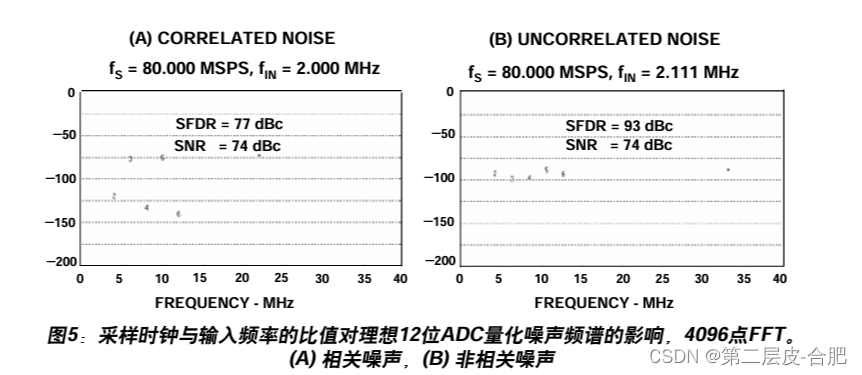
然噪声的均方根值可通过q/√12计算精确近似值,但在某些条件下,频域成分可能与交 流输入信号高度相关。例如,低幅度周期性信号的相关度大于高幅度随机信号的相关度。 通常假设理论量化噪声表现为白噪声,均匀地分布在DC至fs /2的奈奎斯特带宽范围。但 是,事实并非全然如此。在强相关的情况下,量化噪声集中在输入信号的各次谐波上,这 正是我们不希望看到的。 在多数实际应用中,ADC的输入是一段频率(总是会与一些不可避免的系统噪声相加),因 此量化噪声往往是随机的。然而,在频谱分析应用中(或者使用频谱纯净的正弦波作为输 入对ADC执行FFT),量化噪声与信号的相关度取决于采样频率与输入信号的比值。 图5的示例说明了这种情况,其中使用一个4096点FFT来分析一个理想12位ADC的输出。 在左边的FFT图(A)中,采样频率(80.000 MSPS)与输入频率(2.000 MHz)的比值恰好选择为 40,最差谐波比基波低大约77 dB。右图(B)显示了将输入频率略微偏移到2.111 MHz的效 果,表现出随机性相对较高的噪声频谱,此时SFDR约为93 dBc,受FFT噪底尖峰限制。两 种情况下,所有噪声成分的均方根值均近似于q/√12(理论SNR因此为74 dB),但在第一种情 况下,噪声因为相关性而集中在基波谐波上。
相关文章:

SNR = 6.02N + 1.76dB 公式推导
简介 接触ADC或DAC时您一定会碰到这个经常被引用的公式,用于计算转换器理论信噪比 (SNR)。与其盲目地相信表象,不如从根本上了解其来源,因为该公式蕴含着一些微妙之 处,如果不深入探究,可能导致对数据手册技术规格和转…...

归并排序 刷题笔记
归并排序的写法 归并排序 分治双指针 1.定义一个mid if(l>r)return ; 2.分治 sort(q,l,mid); sort(q,mid1,r); 3. 双指针 int il,jmid,k0; 将双序列扫入 缓存数组 条件 while(i<mid&&j<r) 两个数列比较大小 小的一方 进入缓存数组 4. 扫尾 while(…...

字节一面:TCP 和 UDP 可以使用同一个端口吗?
数据包是计算机网络通信的核心,包含头部和数据负载。TCP和UDP协议在传输层使用端口号区分服务和应用。操作系统通过IP头部中的协议字段和端口号来管理网络流量,确保TCP和UDP流量即使共用端口号也不会相互干扰。 在现代计算机网络中,数据传输…...
java guide 八股
Java语言特点 简单易学、面向对象(继承、封装、多态)、平台无关性(Java虚拟机jvm)、支持多线程、可靠、安全、高效、支持网络编程、编译与解释共存 JVM:Java虚拟机(跨平台的关键) JREÿ…...

Windows上使用client-go远程访问安装在本地WMware上的Linux虚拟机里的minikube
我在自己的Windows上安装了WMware,并在WMware上安装了CentOS操作系统,然后在CentOS上创建了一个叫minikube的用户,使用minikube用户启动了一个minikube集群,但是我在Windows上使用client-go并无法连通minikube,搜遍全网…...

Linux/Ubuntu/Debian基本命令:命令行历史记录
一组与类 Unix 环境中的命令行(Terminal)历史记录和命令调用相关的键盘快捷键: Ctrl R: 启动对以前使用过的命令的反向搜索。 当你键入时,它将查找并显示与输入的字符匹配的最新命令。Ctrl G: 退出历史搜索模式,不运行命令。 如…...

倒计时32天
L1-032 Left-pad - 2024团体程序设计天梯赛(历年真题)练习集 (pintia.cn) #include<bits/stdc.h> using namespace std; #define int long long const int N2e56; const int inf0x3f3f3f3f; void solve() {int n;char s;cin>>n>>s;ge…...
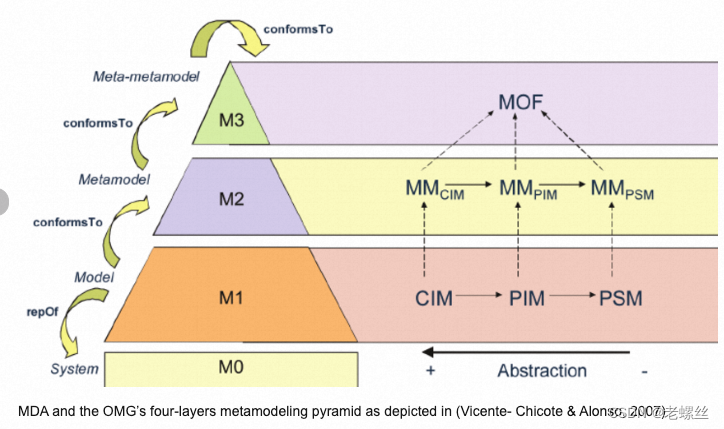
模型驱动架构MDA
MDE 模型驱动工程(MDE, Model-Driven Engineering)是软件工程的一个分支,它将模型与建模拓展到软件开发的所有方面,形成一个多维建模空间,从而将工程活动建立在这些模型的映射和转换之上。[1] MDE的基本原则是将模型视…...

std::error::Error 和 std::io::Error 的区别和用法
std::error::Error 和 std::io::Error 在 Rust 中都是用于错误处理的类型,但它们各自有不同的用途和场景。 std::error::Error: std::error::Error 是一个 trait,它定义了错误处理的基本接口。这个 trait 通常由其他具体的错误类型实现&…...
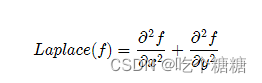
16 OpenCV Laplance算子
文章目录 图像的二阶导数Laplance算子代码示例 图像的二阶导数 在二阶导数的时候,最大变化处的值为零即边缘是零值。通过二阶 导数计算,依据此理论我们可以计算图像二阶导数,提取边缘。 Laplance算子 void Laplacian( InputArray src, Output…...
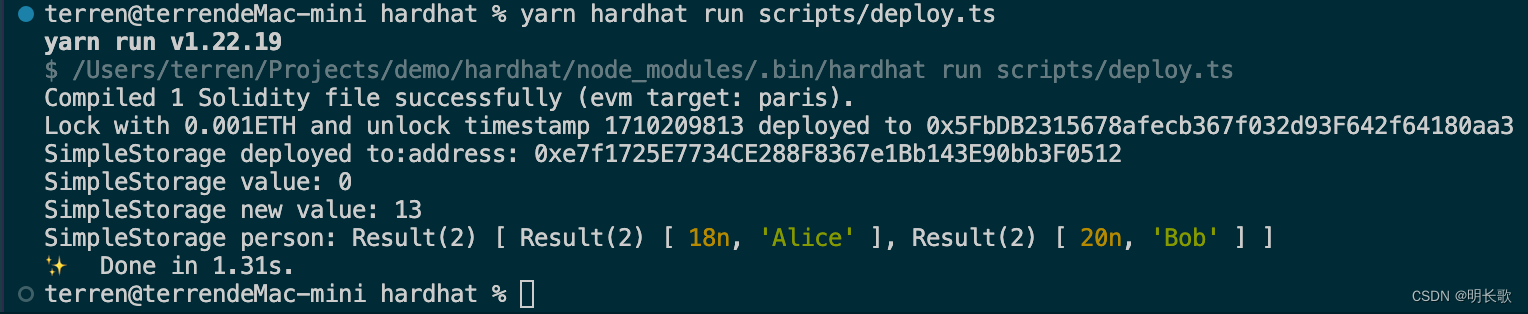
hardhat学习笔记
hardhat学习笔记会不定时填充内容。 初始化项目 yarn init 安装hardhat依赖 yarn add --dev hardhat 初始化 Hardhat yarn hardhat 代码格式化 yarn add --dev prettier prettier-plugin-solidity 项目中增加.prettierrc 与 .prettierignore 配置文件统一格式࿰…...

算法刷题day28
目录 引言一、截断数组二、双端队列三、日期统计 引言 这几道题是周赛里的几道题目,第一道题目我没用这种方法,但还是做出来了,用的一种比较特殊的思考方法,就是把每一个点都判断出来,不满足要求的就舍弃,…...
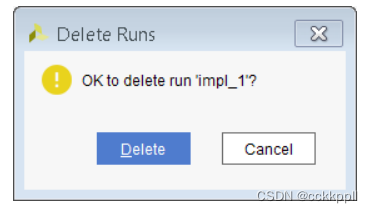
vivado 使用Design Runs窗口、
使用Design Runs窗口 “设计运行”窗口显示在项目中创建的所有合成和实现运行。它包括用于配置、管理和启动运行的命令。 打开Design Run窗口 选择窗口 → Design Runs打开“Design Runs”窗口。 设计运行窗口功能 •每个实现运行都缩进显示在其子级的合成运行下面。 …...

基于YOLOv8的手机摄像头的自动检测系统
文章大纲 数据集网络爬虫开源数据集标注目标定义标注标准标注工具标签更换脚本自制数据集下载地址自动检测系统设计与搭建模型训练与准确率代码仓库下载地址参考文献与学习路径随着移动通信技术的飞速发展,消费者对移动终端的要求也越来越高,各厂商纷纷提出自己的特色卖点,其…...
)
Ubuntu18.04添加内核模块(字符设备)
Ubuntu18.04添加内核模块(字符设备) 虚拟机Ubuntu18.04(内核版本linux-5.4.0-135-generic) 参考 嵌入式Linux驱动开发(一)——字符设备驱动框架入门 1 编译内核模块 创建字符设备代码文件char_dev.c&a…...
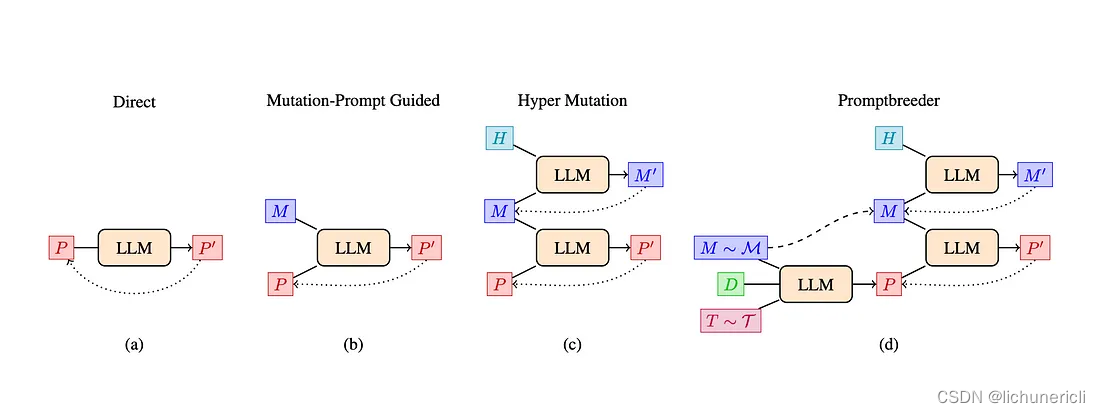
PromptBreeder---针对特定领域演化和发展提示词的方法
原文地址:promptbreeder-evolves-adapts-prompts-for-a-given-domain 论文地址:https://arxiv.org/pdf/2309.16797.pdf 2023 年 10 月 6 日 提示方法分为两大类 硬提示是由人工精心设计的文本提示,包含离散的输入令牌;其缺点…...
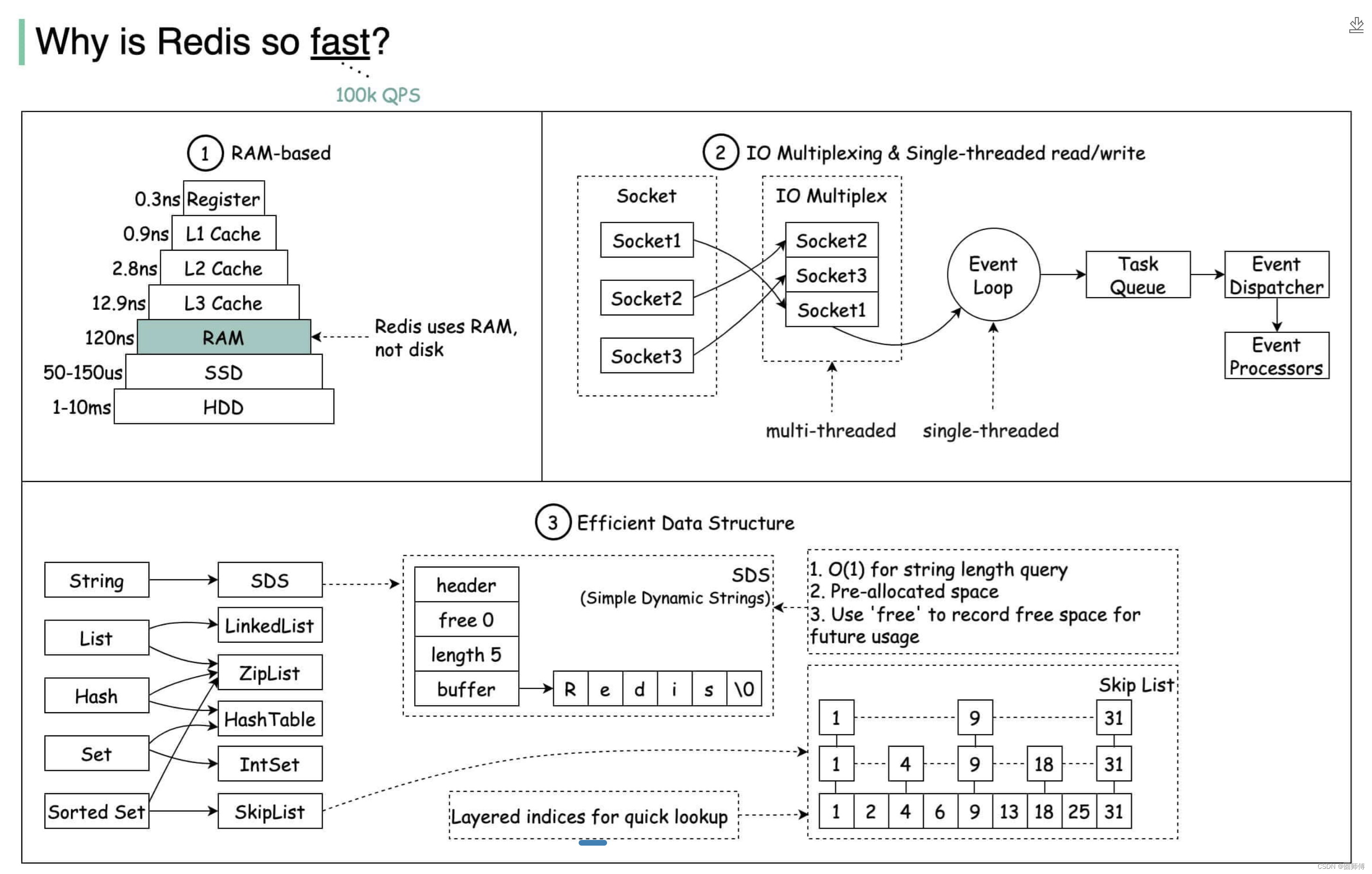
Java后端八股文之Redis
文章目录 1. Redis是什么?2. Redis为什么这么快?3. 为什么要使用缓存?4. Redis几种使用场景:5. Redis的Zset底层为什么要使用跳表而不是平衡树、红黑树或者B树?6.Redis持久化6.1 什么是RDB持久化6.1.1RDB创建快照会阻塞…...

一维数组_与指定数相同的数的个数
任务描述 输出一个整数序列中与指定数字相同的数的个数。 输入格式: 第一行为N,表示整数序列的长度(N < 100); 第二行为N个整数,整数之间以一个空格分开; 第三行包含一个整数,为指定的整数m。输出格式: 输出为N…...
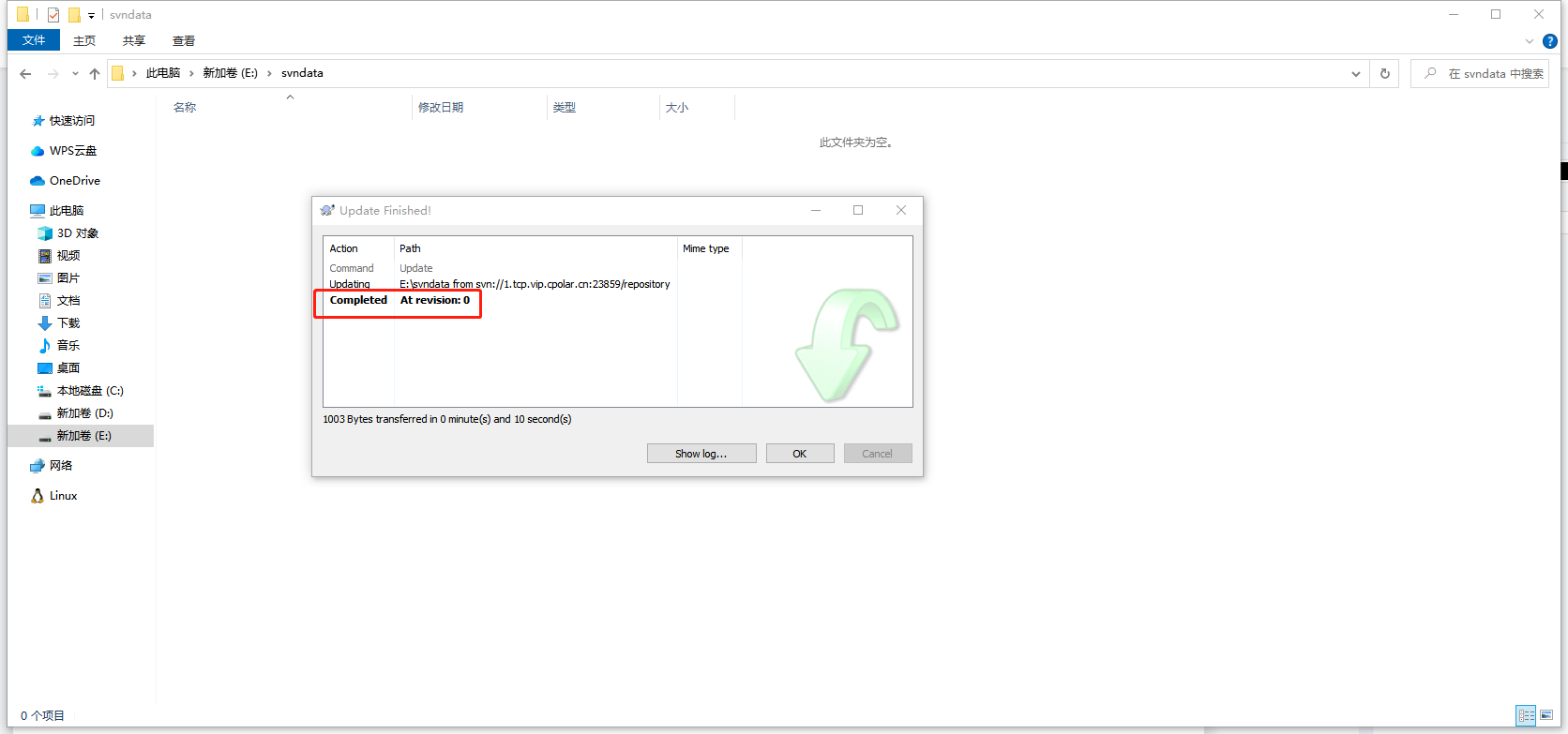
如何在Linux系统安装SVN并配置固定公网地址远程访问【内网穿透】
文章目录 前言1. Ubuntu安装SVN服务2. 修改配置文件2.1 修改svnserve.conf文件2.2 修改passwd文件2.3 修改authz文件 3. 启动svn服务4. 内网穿透4.1 安装cpolar内网穿透4.2 创建隧道映射本地端口 5. 测试公网访问6. 配置固定公网TCP端口地址6.1 保留一个固定的公网TCP端口地址6…...

获取webshell的十种方法
一、直接上传获取webshell 这种对php和jsp的一些程序比较常见,MolyX BOARD就是其中一例,直接在心情图标管理上传。php类型,虽然没有提示,其实已经成功了,上传的文 件url应该是http://forums/images/smiles/下…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
