【动态规划】代码随想录算法训练营第四十六天 |139.单词拆分,关于多重背包,你该了解这些! ,背包问题总结篇!(待补充)
139.单词拆分
1、题目链接:. - 力扣(LeetCode)
2、文章讲解:代码随想录
3、题目:
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
- 输入: s = "leetcode", wordDict = ["leet", "code"]
- 输出: true
- 解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2:
- 输入: s = "applepenapple", wordDict = ["apple", "pen"]
- 输出: true
- 解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
- 注意你可以重复使用字典中的单词。
示例 3:
- 输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
- 输出: false
4、视频链接:
动态规划之完全背包,你的背包如何装满?| LeetCode:139.单词拆分_哔哩哔哩_bilibili
class Solution {public boolean wordBreak(String s, List<String> wordDict) {HashSet<String> set = new HashSet<>(wordDict);boolean[] valid = new boolean[s.length() + 1];valid[0] = true;for (int i = 1; i <= s.length(); i++) {for (int j = 0; j < i && !valid[i]; j++) {if (set.contains(s.substring(j, i)) && valid[j]) {valid[i] = true;}}}return valid[s.length()];}
}// 另一种思路的背包算法
class Solution {public boolean wordBreak(String s, List<String> wordDict) {boolean[] dp = new boolean[s.length() + 1];dp[0] = true;for (int i = 1; i <= s.length(); i++) {for (String word : wordDict) {int len = word.length();if (i >= len && dp[i - len] && word.equals(s.substring(i - len, i))) {dp[i] = true;break;}}}return dp[s.length()];}
}多重背包理论基础
对于多重背包,我在力扣上还没发现对应的题目,所以这里就做一下简单介绍,大家大概了解一下。
有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
多重背包和01背包是非常像的, 为什么和01背包像呢?
每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
例如:
背包最大重量为10。
物品为:
| 重量 | 价值 | 数量 | |
| 物品0 | 1 | 15 | 2 |
| 物品1 | 3 | 20 | 3 |
| 物品2 | 4 | 30 | 2 |
问背包能背的物品最大价值是多少?
和如下情况有区别么?
| 重量 | 价值 | 数量 | |
| 物品0 | 1 | 15 | 1 |
| 物品0 | 1 | 15 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品2 | 4 | 30 | 1 |
| 物品2 | 4 | 30 | 1 |
毫无区别,这就转成了一个01背包问题了,且每个物品只用一次。
练习题目:卡码网第56题,多重背包(opens new window)
代码如下:
// 超时了
#include<iostream>
#include<vector>
using namespace std;
int main() {int bagWeight,n;cin >> bagWeight >> n;vector<int> weight(n, 0); vector<int> value(n, 0);vector<int> nums(n, 0);for (int i = 0; i < n; i++) cin >> weight[i];for (int i = 0; i < n; i++) cin >> value[i];for (int i = 0; i < n; i++) cin >> nums[i]; for (int i = 0; i < n; i++) {while (nums[i] > 1) { // 物品数量不是一的,都展开weight.push_back(weight[i]);value.push_back(value[i]);nums[i]--;}}vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍历物品,注意此时的物品数量不是nfor(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}大家去提交之后,发现这个解法超时了,为什么呢,哪里耗时呢?
耗时就在 这段代码:
for (int i = 0; i < n; i++) {while (nums[i] > 1) { // 物品数量不是一的,都展开weight.push_back(weight[i]);value.push_back(value[i]);nums[i]--;}
}如果物品数量很多的话,C++中,这种操作十分费时,主要消耗在vector的动态底层扩容上。(其实这里也可以优化,先把 所有物品数量都计算好,一起申请vector的空间。
这里也有另一种实现方式,就是把每种商品遍历的个数放在01背包里面在遍历一遍。
代码如下:(详看注释)
#include<iostream>
#include<vector>
using namespace std;
int main() {int bagWeight,n;cin >> bagWeight >> n;vector<int> weight(n, 0);vector<int> value(n, 0);vector<int> nums(n, 0);for (int i = 0; i < n; i++) cin >> weight[i];for (int i = 0; i < n; i++) cin >> value[i];for (int i = 0; i < n; i++) cin >> nums[i];vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < n; i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量// 以上为01背包,然后加一个遍历个数for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}}cout << dp[bagWeight] << endl;
}时间复杂度:O(m × n × k),m:物品种类个数,n背包容量,k单类物品数量
从代码里可以看出是01背包里面在加一个for循环遍历一个每种商品的数量。 和01背包还是如出一辙的。
当然还有那种二进制优化的方法,其实就是把每种物品的数量,打包成一个个独立的包。
和以上在循环遍历上有所不同,因为是分拆为各个包最后可以组成一个完整背包,具体原理我就不做过多解释了,大家了解一下就行,面试的话基本不会考完这个深度了,感兴趣可以自己深入研究一波。
#总结
多重背包在面试中基本不会出现,力扣上也没有对应的题目,大家对多重背包的掌握程度知道它是一种01背包,并能在01背包的基础上写出对应代码就可以了。
至于背包九讲里面还有混合背包,二维费用背包,分组背包等等这些,大家感兴趣可以自己去学习学习,这里也不做介绍了,面试也不会考。
背包问题汇总
年前我们已经把背包问题都讲完了,那么现在我们要对背包问题进行总结一番。
背包问题是动态规划里的非常重要的一部分,所以我把背包问题单独总结一下,等动态规划专题更新完之后,我们还会在整体总结一波动态规划。
关于这几种常见的背包,其关系如下:
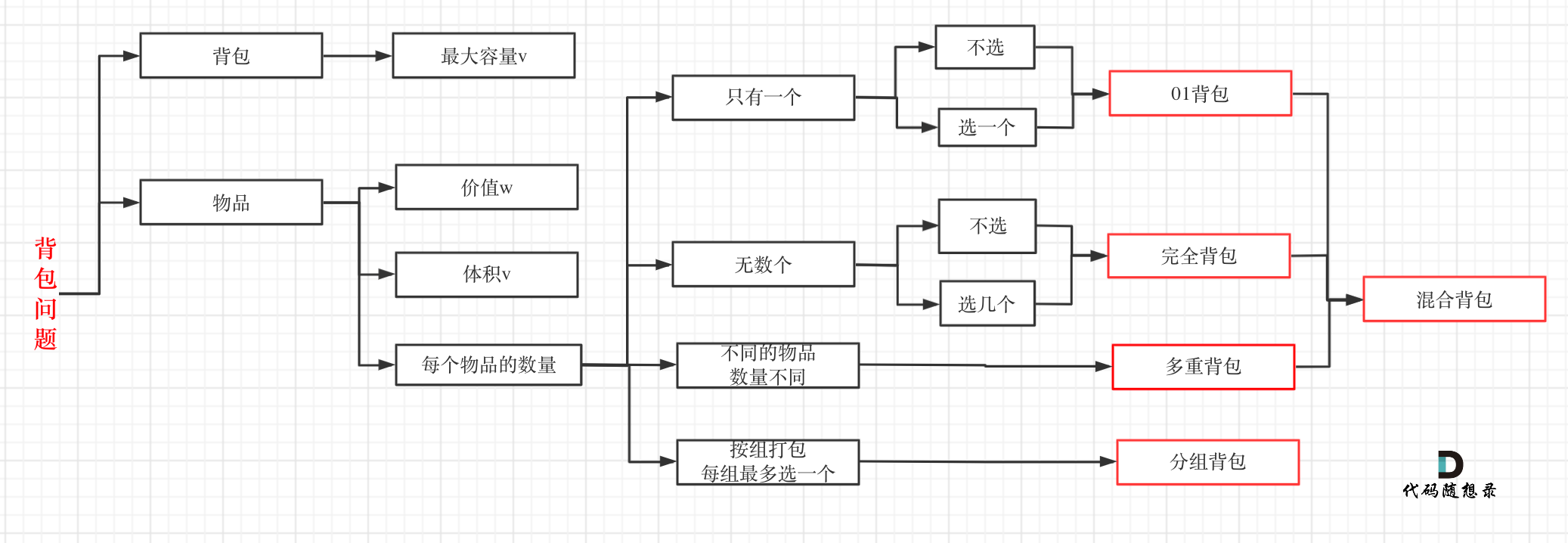
通过这个图,可以很清晰分清这几种常见背包之间的关系。
在讲解背包问题的时候,我们都是按照如下五部来逐步分析,相信大家也体会到,把这五部都搞透了,算是对动规来理解深入了。
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
其实这五部里哪一步都很关键,但确定递推公式和确定遍历顺序都具有规律性和代表性,所以下面我从这两点来对背包问题做一做总结。
#背包递推公式
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
- 动态规划:416.分割等和子集(opens new window)
- 动态规划:1049.最后一块石头的重量 II(opens new window)
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
- 动态规划:494.目标和(opens new window)
- 动态规划:518. 零钱兑换 II(opens new window)
- 动态规划:377.组合总和Ⅳ(opens new window)
- 动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
- 动态规划:474.一和零(opens new window)
问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
- 动态规划:322.零钱兑换(opens new window)
- 动态规划:279.完全平方数(opens new window)
#遍历顺序
#01背包
在动态规划:关于01背包问题,你该了解这些!(opens new window)中我们讲解二维dp数组01背包先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
和动态规划:关于01背包问题,你该了解这些!(滚动数组)(opens new window)中,我们讲解一维dp数组01背包只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。
一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的,大家需要注意!
#完全背包
说完01背包,再看看完全背包。
在动态规划:关于完全背包,你该了解这些!(opens new window)中,讲解了纯完全背包的一维dp数组实现,先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
但是仅仅是纯完全背包的遍历顺序是这样的,题目稍有变化,两个for循环的先后顺序就不一样了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
相关题目如下:
- 求组合数:动态规划:518.零钱兑换II(opens new window)
- 求排列数:动态规划:377. 组合总和 Ⅳ(opens new window)、动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
如果求最小数,那么两层for循环的先后顺序就无所谓了,相关题目如下:
- 求最小数:动态规划:322. 零钱兑换(opens new window)、动态规划:279.完全平方数(opens new window)
对于背包问题,其实递推公式算是容易的,难是难在遍历顺序上,如果把遍历顺序搞透,才算是真正理解了。
#总结
这篇背包问题总结篇是对背包问题的高度概括,讲最关键的两部:递推公式和遍历顺序,结合力扣上的题目全都抽象出来了。
而且每一个点,我都给出了对应的力扣题目。
最后如果你想了解多重背包,可以看这篇动态规划:关于多重背包,你该了解这些!(opens new window),力扣上还没有多重背包的题目,也不是面试考察的重点。
如果把我本篇总结出来的内容都掌握的话,可以说对背包问题理解的就很深刻了,用来对付面试中的背包问题绰绰有余!
背包问题总结:
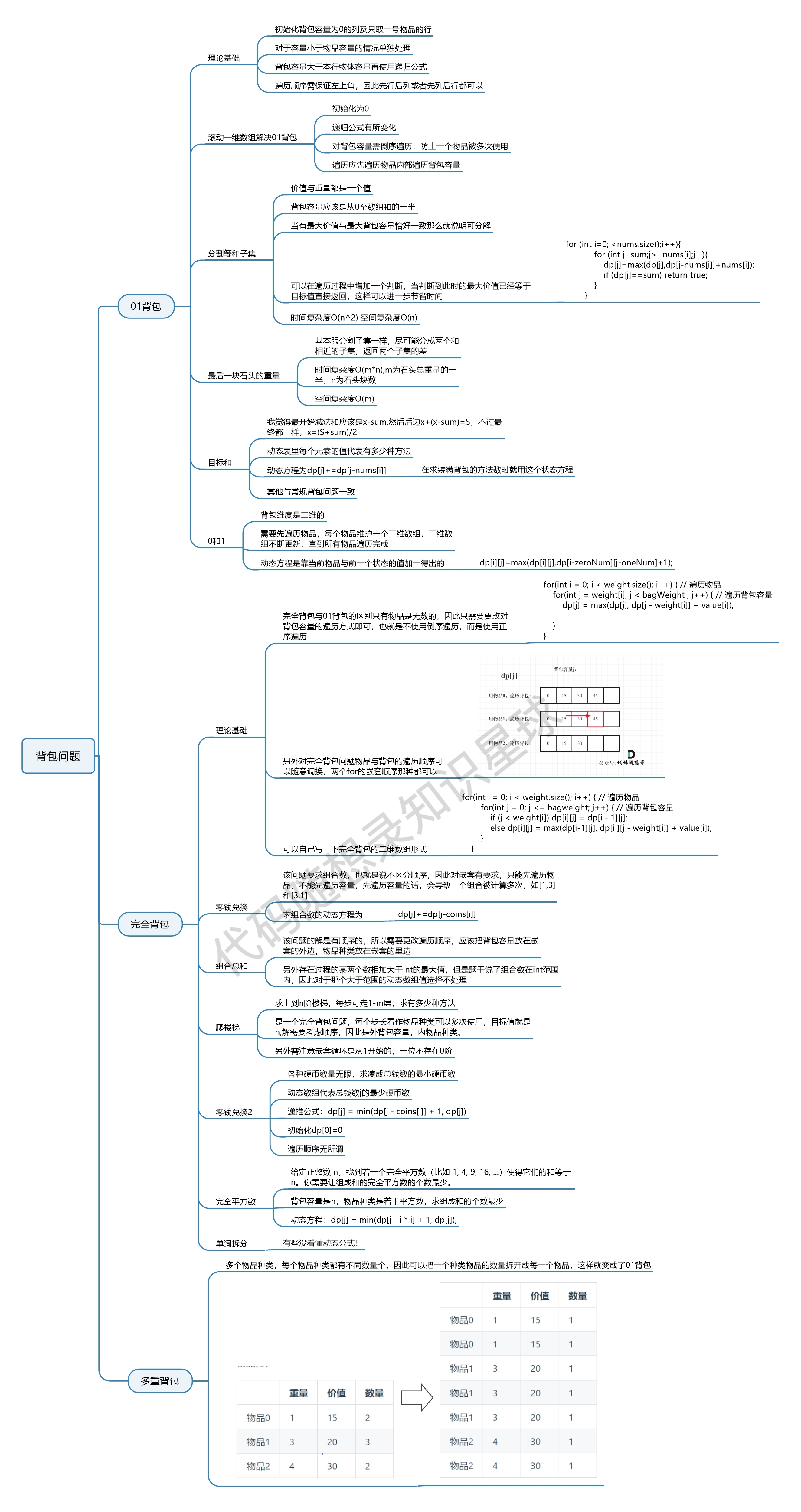
相关文章:

【动态规划】代码随想录算法训练营第四十六天 |139.单词拆分,关于多重背包,你该了解这些! ,背包问题总结篇!(待补充)
139.单词拆分 1、题目链接:. - 力扣(LeetCode) 2、文章讲解:代码随想录 3、题目: 给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词…...
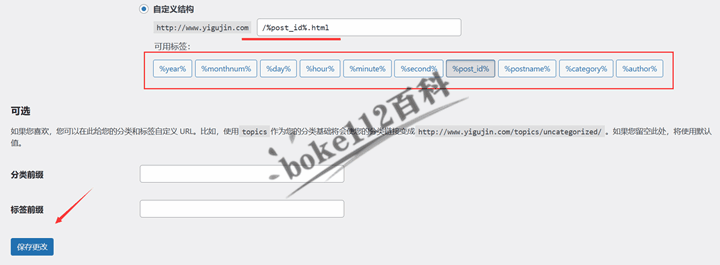
WordPress建站入门教程:如何选择和设置固定链接结构?
我们成功搭建好WordPress网站后,发布的文章对应的URL地址默认是使用“日期和名称型”,即是网站域名跟着的是年月日,最后是文章标题,如http://www.yigujin.com/2024/03/06/免费响应式WordPress博客主题JianYue/ 为了让我们的文章U…...

一款好用的AI工具——边界AICHAT(三)
目录 3.23、文档生成PPT演示3.24、AI文档翻译3.25、AI翻译3.26、论文模式3.27、文章批改3.28、文章纠正3.29、写作助手3.30、文言文翻译3.31、日报周报月报生成器3.32、OCR-DOC办公文档识别3.33、AI真人语音合成3.34、录音音频总结3.35、域方模型市场3.36、模型创建3.37、社区交…...

编程示例: 矩阵的多项式计算以javascript语言为例
编程示例: 矩阵的多项式计算以javascript语言为例 国防工业出版社的《矩阵理论》一书中第一章第8个习题 试计算2*A^8-3*A^5A^4A^2-4I A[[1,0,2],[0,-1,1],[0,1,0]] 代码如下 <html> <head> <title> 矩阵乘法 </title> <script srcset.js ><…...

project generator 简单使用
文章目录 1 progen 资源2 使用简介2.1 安装2.2 添加 target(可选)2.3 替换 CMake 模板(可选)2.4 创建 progen 项目 3 总结 1 progen 资源 0)简介:progen(project-generator,项目生成…...
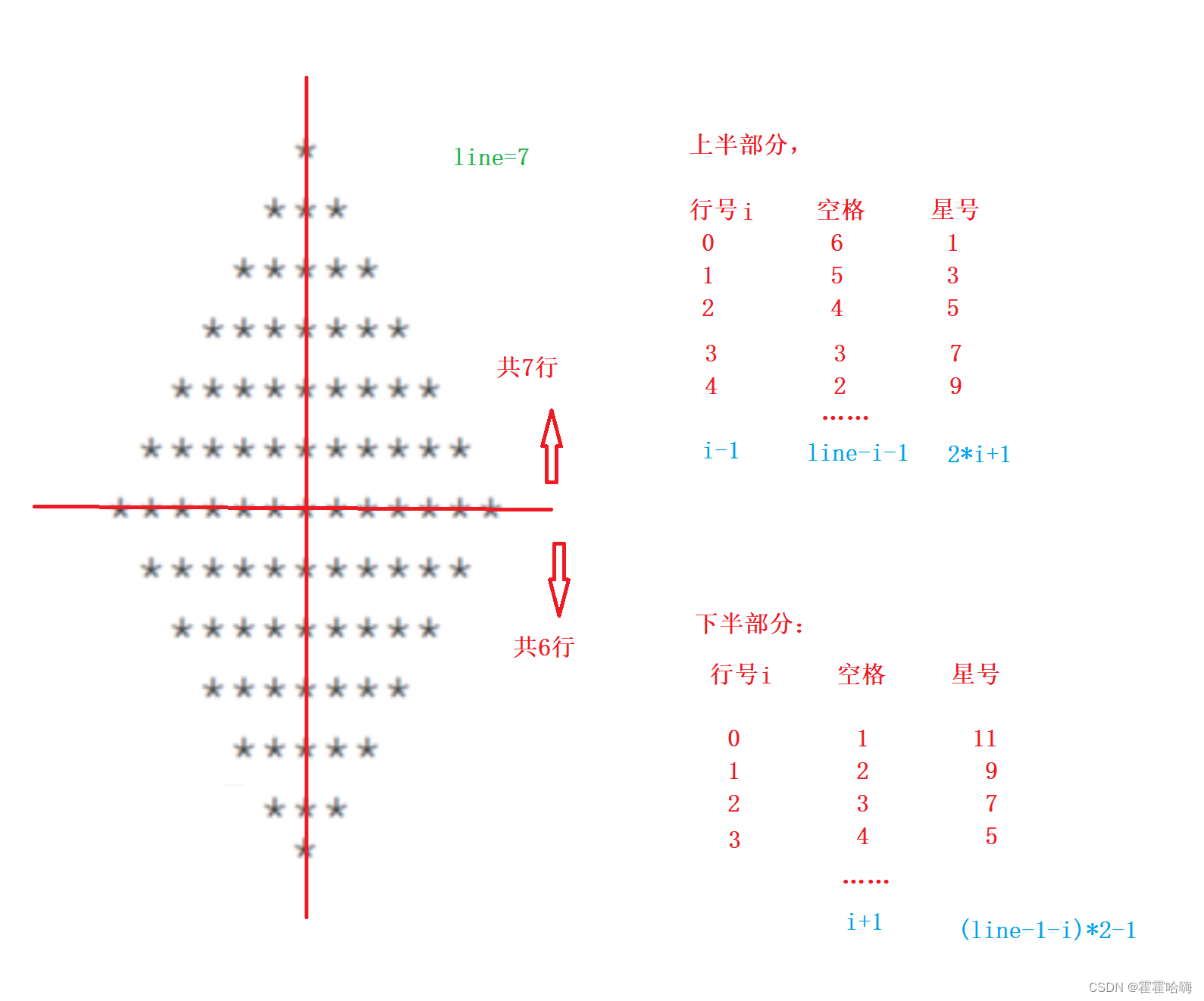
C语言 —— 图形打印
题目1: 思路: 如果我们要打印一个实心正方形,其实就是一个二维数组,i控制行,j控制列,行列不需要控制,arr[i][j]直接打印星号即可。 对于空心正方形,我们只需要控制行和列的条件&…...
常用模块)
Python基础学习(11)常用模块
文章目录 一、time二、random三、os四、sys五、json补充1:JSON字符串补充2:JSON字符串和字典的区别 六、hashlib Python基础学习(1)基本知识 Python基础学习(2)序列类型方法与数据类型转换 Python基础学习(3)进阶字符串(格式化输出) Python基础学习(4)散…...
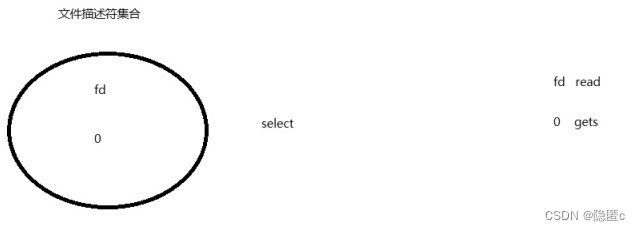
嵌入式学习37-TCP并发模型
TCP并发模型: 1.TCP多线程模型: 缺点: 1.创建线程会带来 资源开销 2.能够实现的 并发量 比较有限 2.IO模型: 1.阻塞IO: 没有…...

C语言字符函数和字符串函数
前言 今天这篇博客咱们一起来认识一些特殊的函数,在编程的过程中,我们经常要处理字符和字符串,为了方便字符和字符串,C语言提供了一些库函数,让我们一起看看这些函数都有什么功能吧!!࿰…...

Go语言必知必会100问题-22 空切片与nil切片有区别吗?
空切片与nil切片有区别吗? 很多开发人员经常混淆nil切片和空切片,不清楚什么时候使用空切片什么时候使用nil,而有些库函数又对这两者使用进行了区分。下面先来看看它们的定义。 空切片是length为0的切片当切片等于nil时为nil切片 下面是几种不同空切片…...
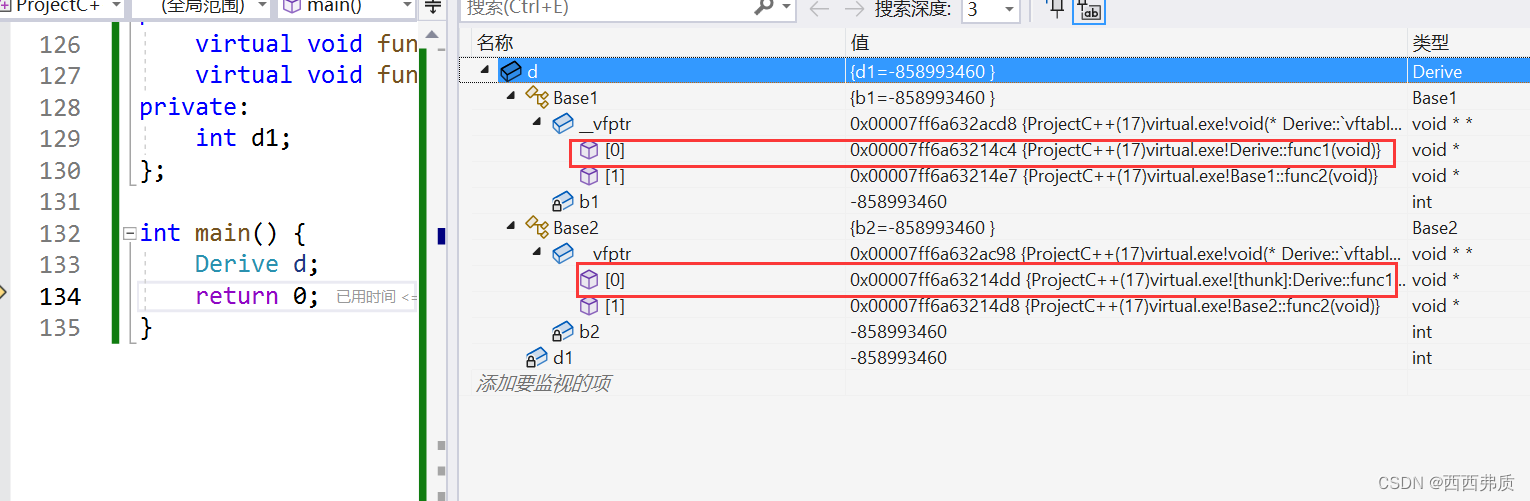
【C++进阶】C++多态概念详解
C多态概念详解 一,多态概念二,多态的定义2.1 多态构成的条件2.2 什么是虚函数2.3 虚函数的重写2.3.1 虚函数重写的特例2.3.2 override和final 2.4 重载和重写(覆盖)和重定义(隐藏)的区别 三,抽象…...
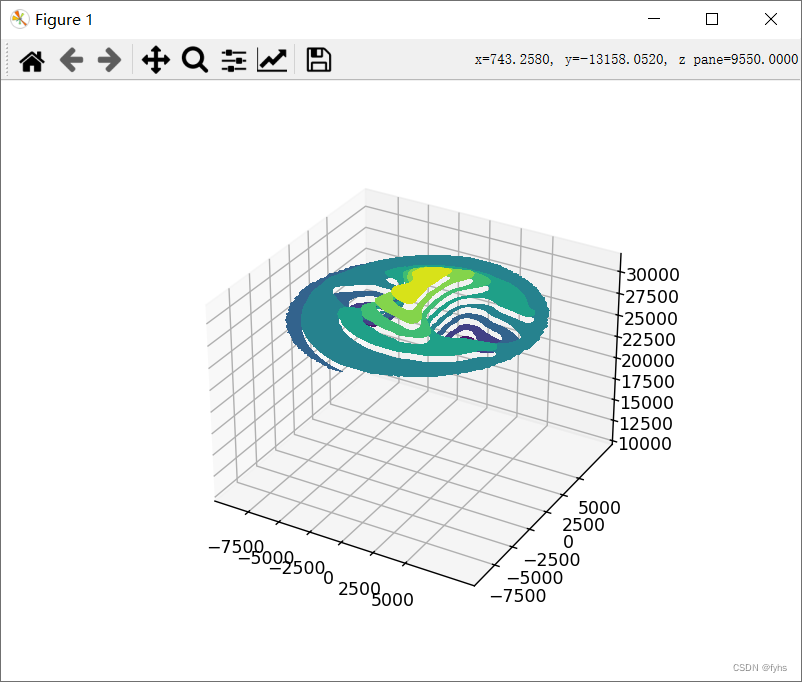
Python 导入Excel三维坐标数据 生成三维曲面地形图(面) 2、线条平滑曲面但有间隔
环境和包: 环境 python:python-3.12.0-amd64包: matplotlib 3.8.2 pandas 2.1.4 openpyxl 3.1.2 scipy 1.12.0 代码: import pandas as pd import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from scipy.interpolate import griddata imp…...
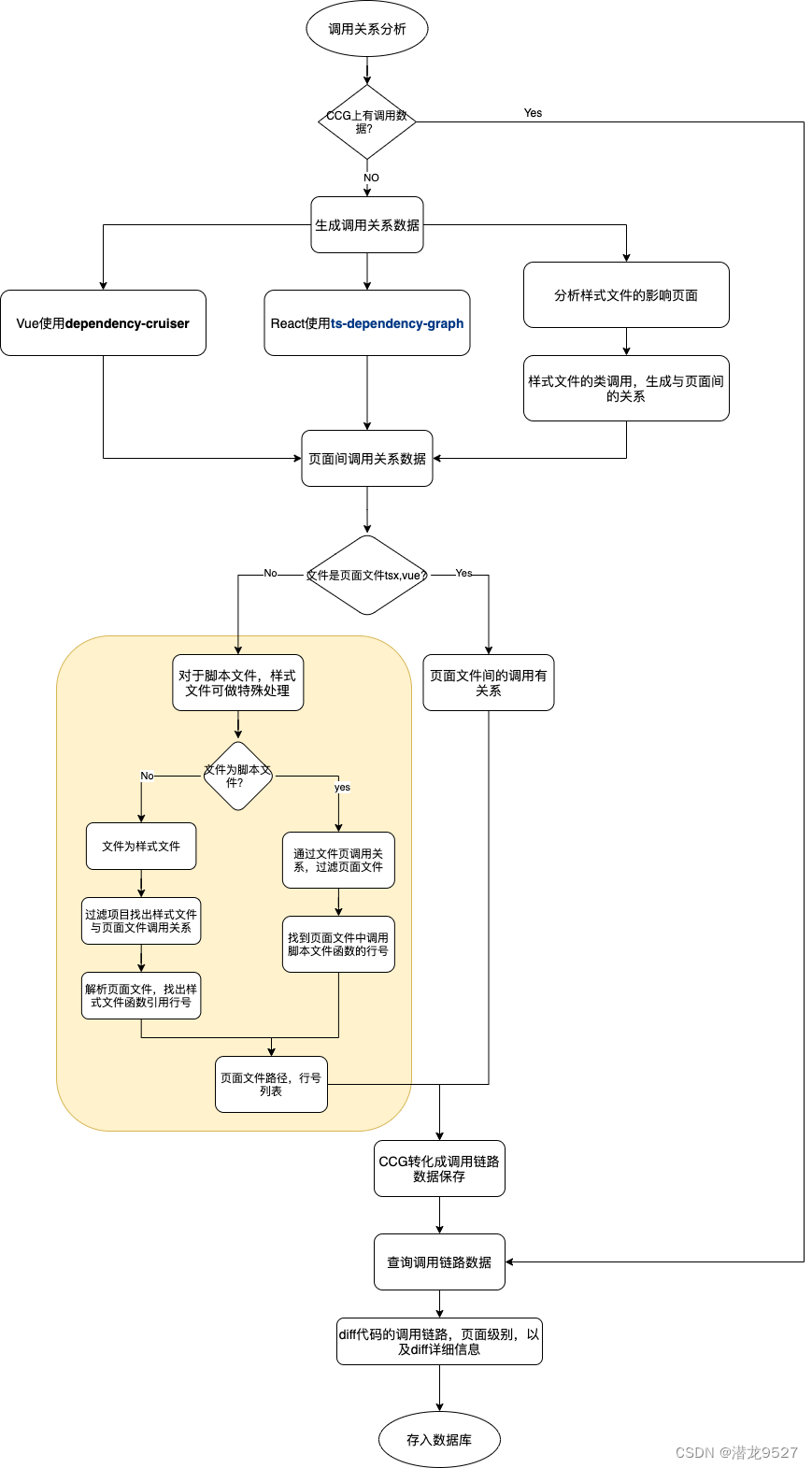
前端精准测试调用链路分析
精准测试在评估需求的测试范围时,需要评估一下代码的影响范围,这个范围有两部分:一是需求直接修改的代码;二是修改代码影响到的功能模块。代码影响到的功能一般是通过调用链路分析来实现的,java和kotlin代码可以由java…...

Objective-C blocks 概要
1.block的使用 1.1什么是block? Blocks是C语言的扩充功能:带有自动变量(局部变量)的匿名函数。 “带有自动变量”在Blocks中表现为“截取自动变量" “匿名函数”就是“不带名称的函数” 块,封装了函数调用及调用…...
Linux操作系统-07-Linux安装应用
一、使用rpm安装应用(不推荐) 先下载到本地,以.rpm文件名结尾,下载完成后,再安装 rpm -qa | grep mysql #查询当前系统是否有下载过mysql包 先上传mysql的rpm安装包到linux的opt目录 安装 rpm -ivh …...

DevOps实战:Docker、Kubernetes与Jenkins的完美融合
DevOps与容器化技术:Docker、Kubernetes和Jenkins 引言 在软件开发领域,DevOps文化和容器化技术已经成为当今最热门的话题之一。DevOps的目标是缩短开发和运维之间的距离,提高软件交付的速度和质量。而容器化技术,如Docker和Kub…...

Python面向对象——程序架构
需求 创建图形管理器 -记录多种图形(圆形、矩形.) --提供计算总面积的方法, 要求:增加新图形,不影响图形管理器 测试: 创建图形管理器,存储多个图形对象。 通过图形管理器,调用计算总面积方法 思路 代码 # ------…...

springboot单体项目链路日志跟踪及接口耗时
最近接触一个新的传统项目,在联调过程中,查看日志特别不方便,既无trackId,即无接口耗时,所以写了该博客。话不多说,直接上代码 1、实体类user package com.yk.domain;import lombok.Data;@Data public class User {private Long id;private String username;private St…...

力扣hot---岛屿数量
dfs思路: 首先通过两层for循环遍历每一个点,如果这个点为0或者2(这个2是什么呢?是在遍历该点以及该点连成的这一片区域中,因为通过深度优先搜索,遍历该点就等于遍历这一片区域,遍历这篇区域中的…...
如何在Linux使用docker安装Plik并实现无公网ip上传下载内网存储的文件资源
文章目录 1. Docker部署Plik2. 本地访问Plik3. Linux安装Cpolar4. 配置Plik公网地址5. 远程访问Plik6. 固定Plik公网地址7. 固定地址访问Plik 正文开始前给大家推荐个网站,前些天发现了一个巨牛的 人工智能学习网站, 通俗易懂,风趣幽默&…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...
