当前位置： 首页 > news >正文

【DAY11 软考中级备考笔记】数据结构 查找和排序

news 2026/2/9 0:16:22

数据结构 查找和排序 3月12日 – 天气：晴

1. 顺序查找

在这里插入图片描述

顺序查找就是简单的从头一个一个的进行比较，注意它的平均查找长度

2. 折半查找

在这里插入图片描述

折半查找和二叉排序树一致：

优点：查找效率很高

缺点：要求必须是循序存储并且表中元素必须有序

3. 分块查找

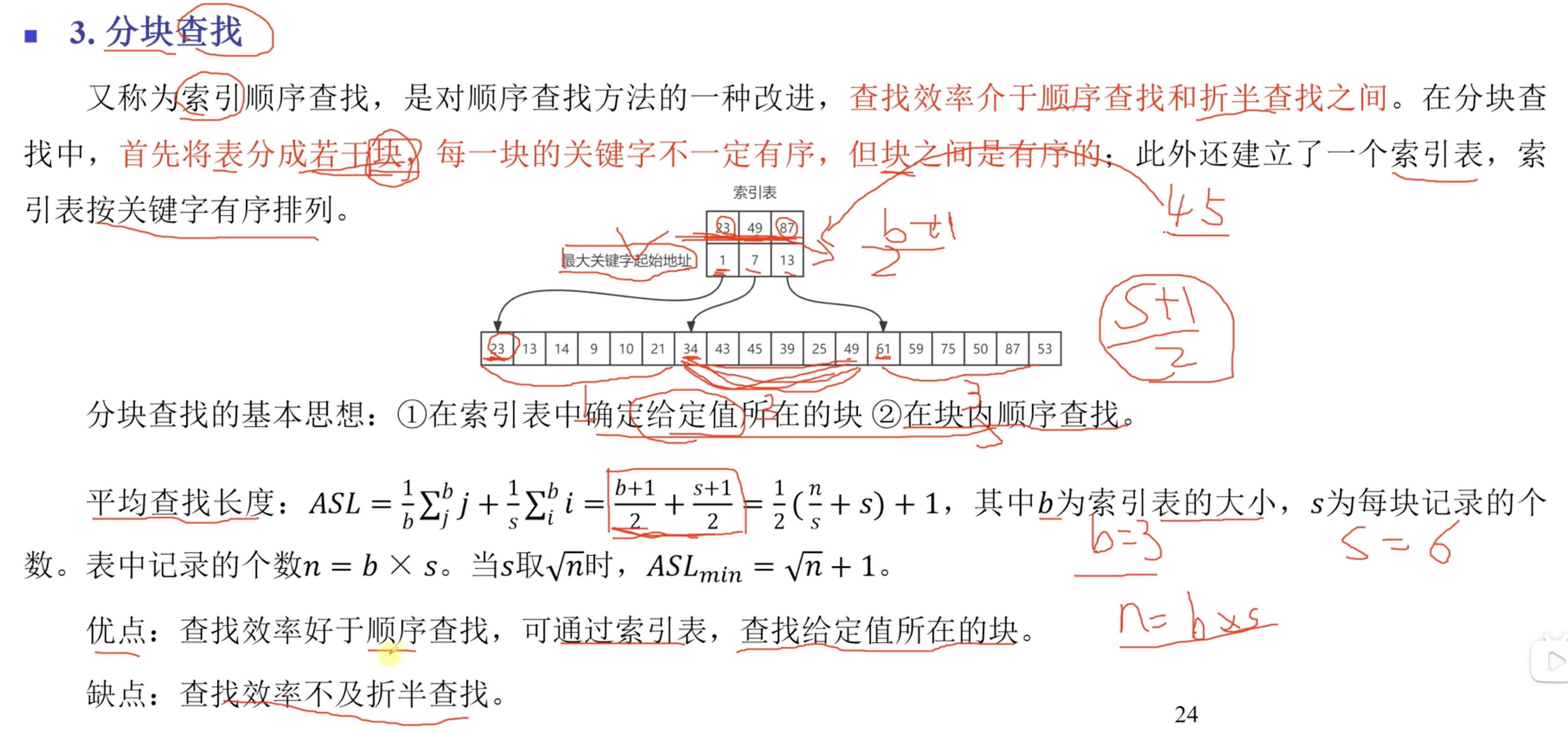
image-20240312204445143

分块查找实际上是结合了折半查找和顺序查找两种方式。

注意ASL的计算方式

优点：查找效率高于顺序查找，低于折半查找

4. 哈希表

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

使用取余的方法，需要注意取余的值：

取余的那个值 大于等于元素个数，小于等于比当前个数大的第一个质数。假设元素个数为9，则m的取值范围为【9，11】

image-20240312205703780

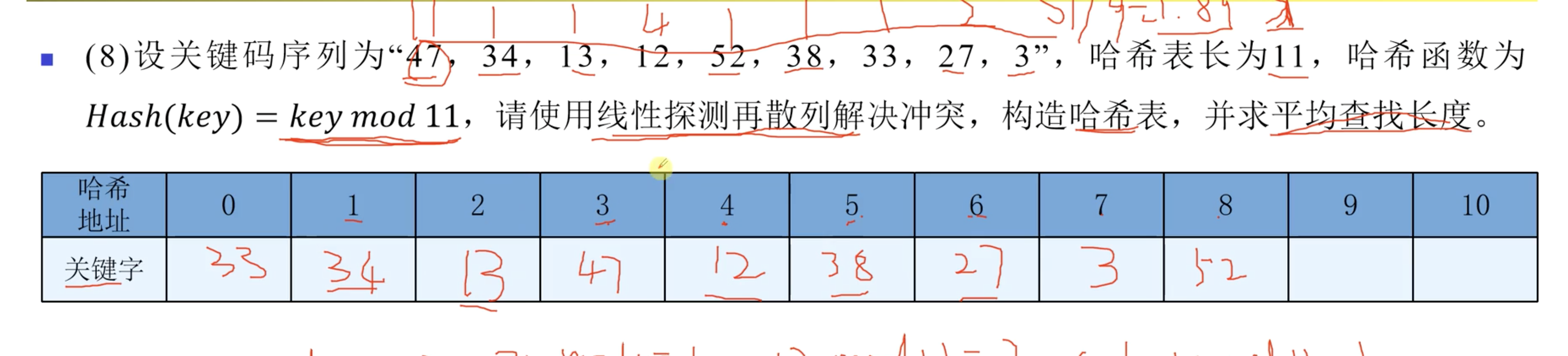
image-20240312205738937

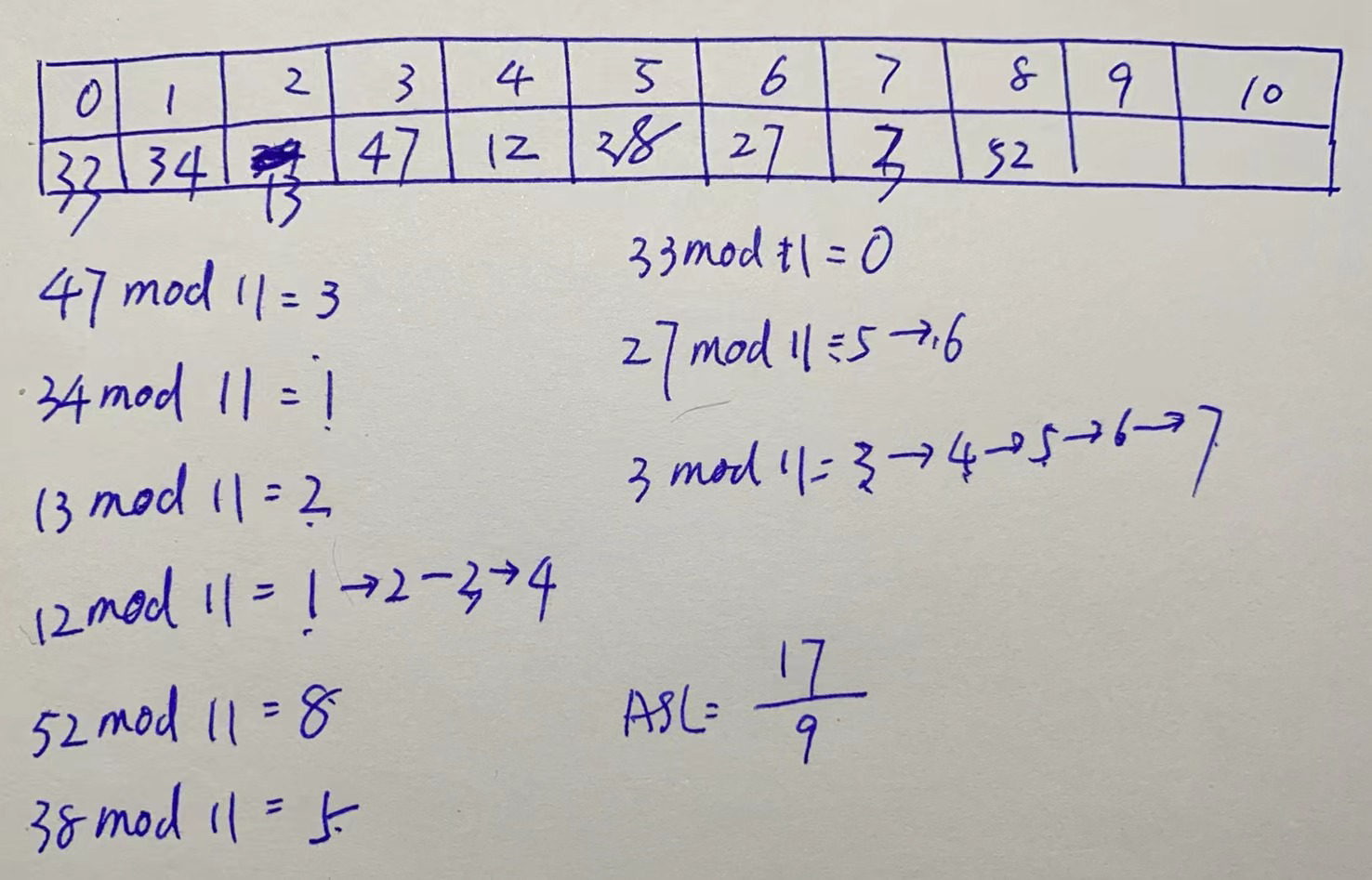
image-20240312205720498

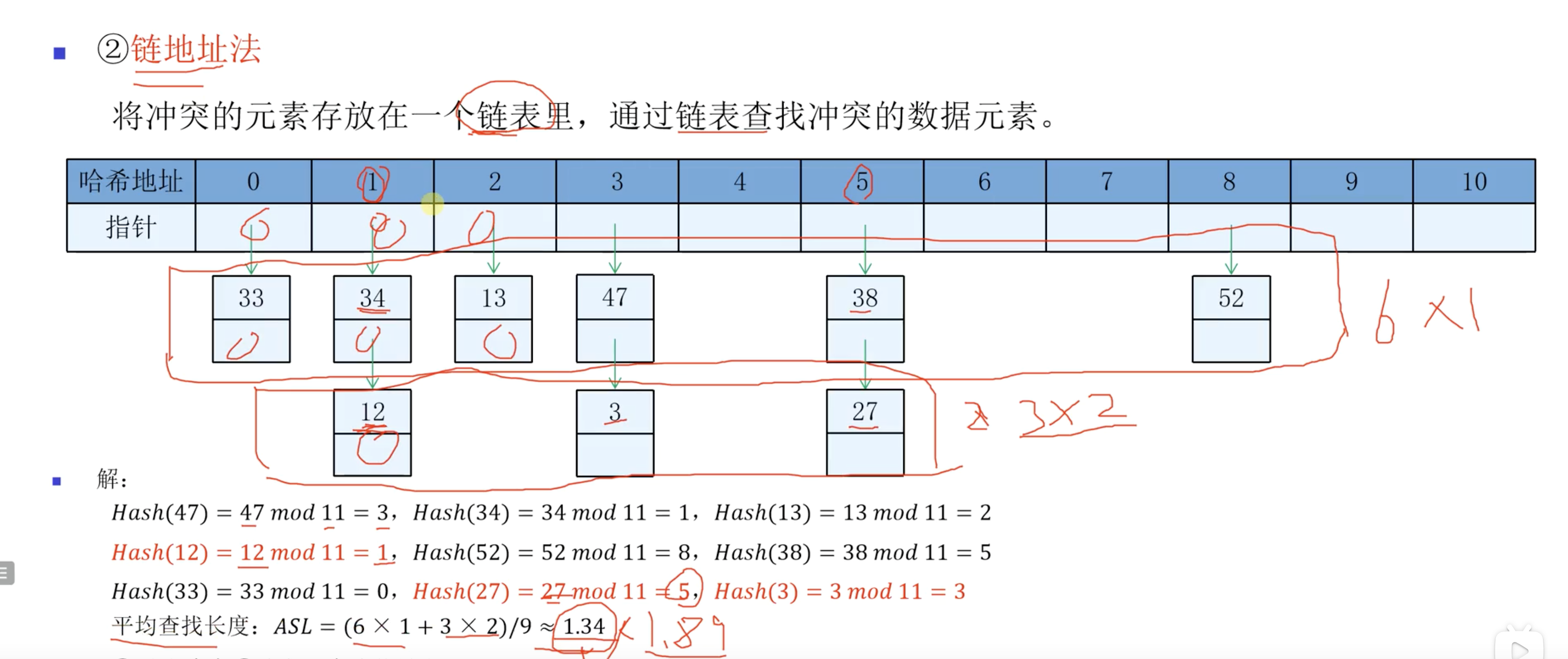
image-20240312205751411

采用链地址法的优点和不足：

  • 优点：平均查找长度短
  • 缺点：需要存储大量的指针，导致空间的浪费

image-20240312205855799

5. 直接插入排序

image-20240312210000626

  • 思想：直接插入排序的思想是向序列分为有序序列和无序序列。每次都从无序序列中取出一个值，然后跟有序序列的值一次进行比较，找到和事的位置进行插入。

  • 确定性：因此插入排序中在未完成时，没有一个元素的值时确定的。

  • 稳定性：稳定的

  • 时间复杂度：最好的情况下，只需要比较n-1次，最坏的情况是n^2

  • 空间复杂度：1

6. 希尔排序

image-20240312210356091

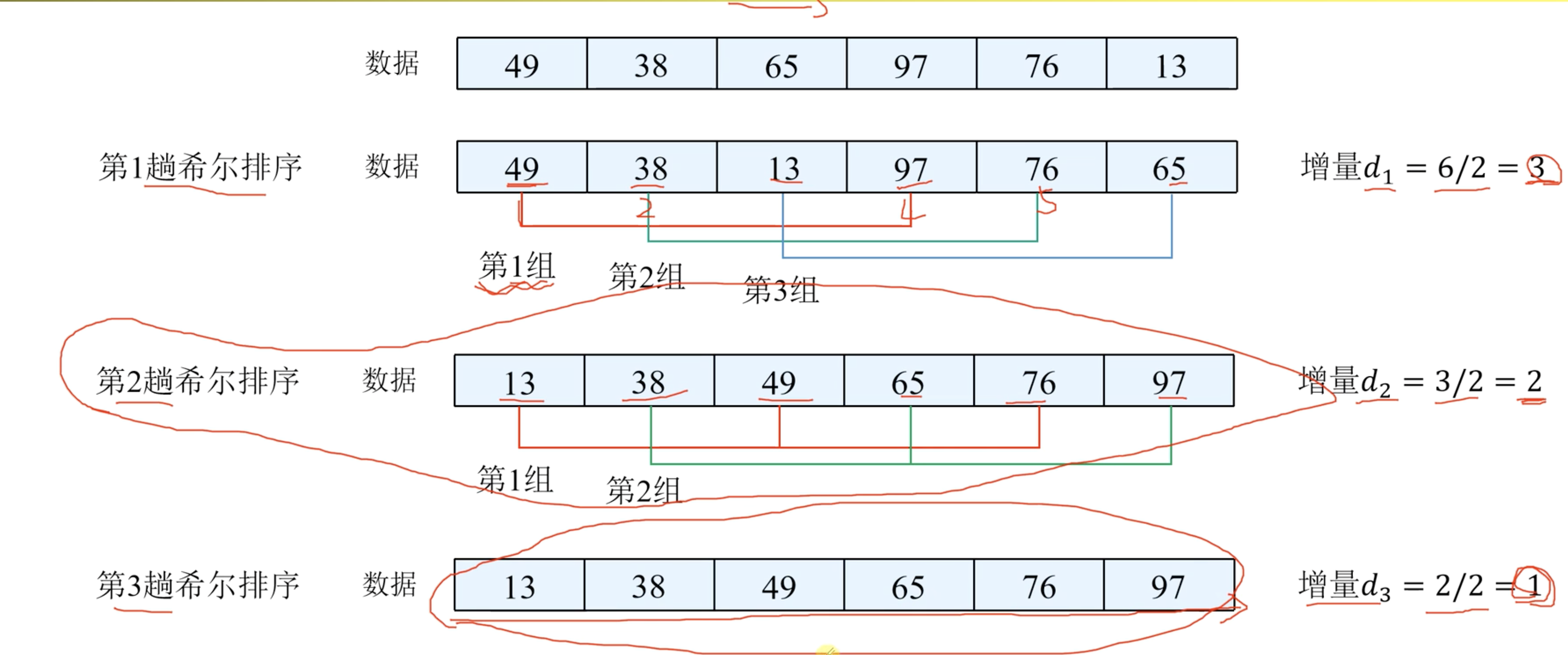
image-20240312211410777

  • 思想：希尔排序是直接插入排序的改进。它首先将元素进行分组，在组内进行直接插入排序，随着增量的逐渐减小，最终使得整个序列都有序
  • 确定性：不确定
  • 稳定性：不稳定
  • 时间复杂度：n^1.3
  • 空间复杂度：1

希尔排序最后一次排序为直接插入排序

7. 冒泡排序

image-20240312211543453

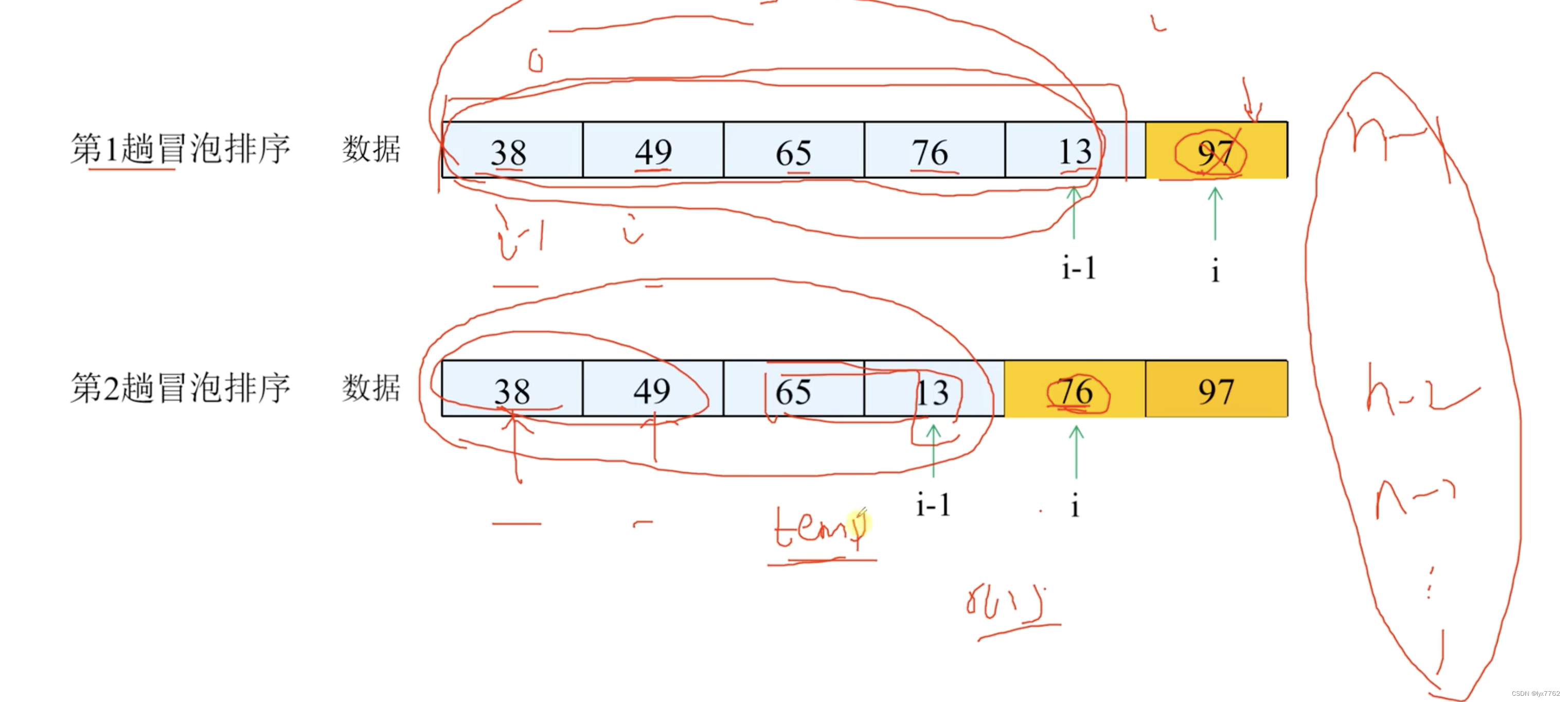
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

  • 思想：两两比较元素，将如果次序相反，则交换。这样每一轮排序都会选出最大的或者最小的元素，直到所有的元素都有序
  • 稳定性：稳定
  • 确定性：确定，每一次都会选择出最大的元素，且该元素的位置不会再次发生变化
  • 时间复杂度 n^2
  • 空间复杂度 1

8. 快速排序

image-20240312212009856

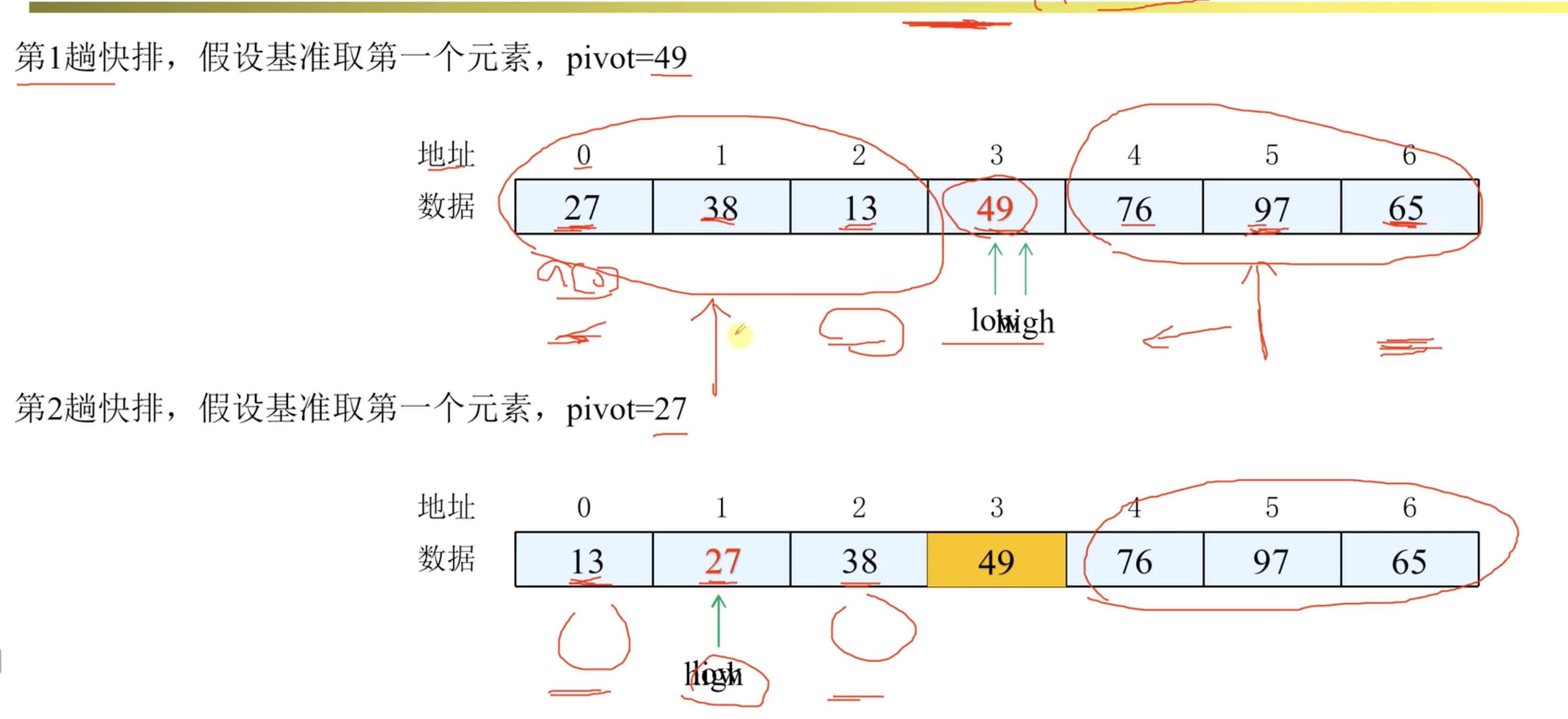
image-20240312212031166

  • 思想：在序列中任意选择一个元素，然后以这个元素为基准，将小于它的元素都放在它的左边，大于它的都放在右边。然后生成两个子序列。然后这两个子序列再一次执行上述操作。直到序列中只有一个元素
  • 稳定性：不稳定
  • 确定性：每次所选择的这个元素的位置是固定的
  • 时间复杂度：nlog
  • 空间复杂度：log （递归）

9. 简单选择排序

image-20240312212827496

image-20240312213156022

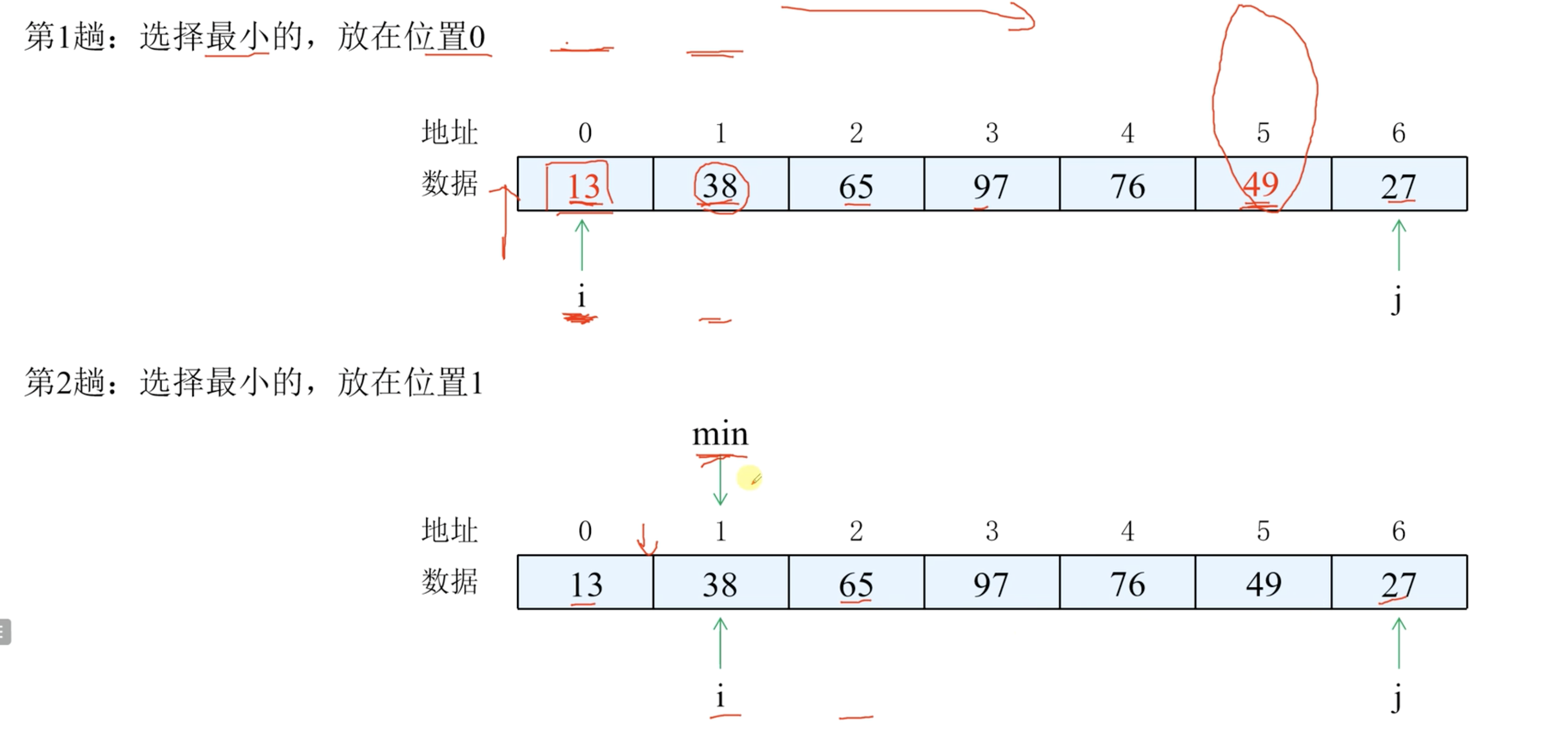
  • 思想：每次从带排序的序列中找到最小的元素，然后放在有序序列末尾。这里注意和直接插入排序区分。直接插入的思想是每一次都从未排序的序列中选择一个元素，然后放到已经排序序列里面的合适的位置
  • 稳定性：不稳定
  • 确定性：确定
  • 时间复杂度 n^2
  • 空间复杂度：1

相关文章：

【DAY11 软考中级备考笔记】数据结构 查找和排序

数据结构 查找和排序 3月12日 – 天气：晴 1. 顺序查找 顺序查找就是简单的从头一个一个的进行比较，注意它的平均查找长度 2. 折半查找 折半查找和二叉排序树一致： 优点：查找效率很高 缺点：要求必须是循序存储并且表中…...

编程日记 2024/3/13 5:26:44

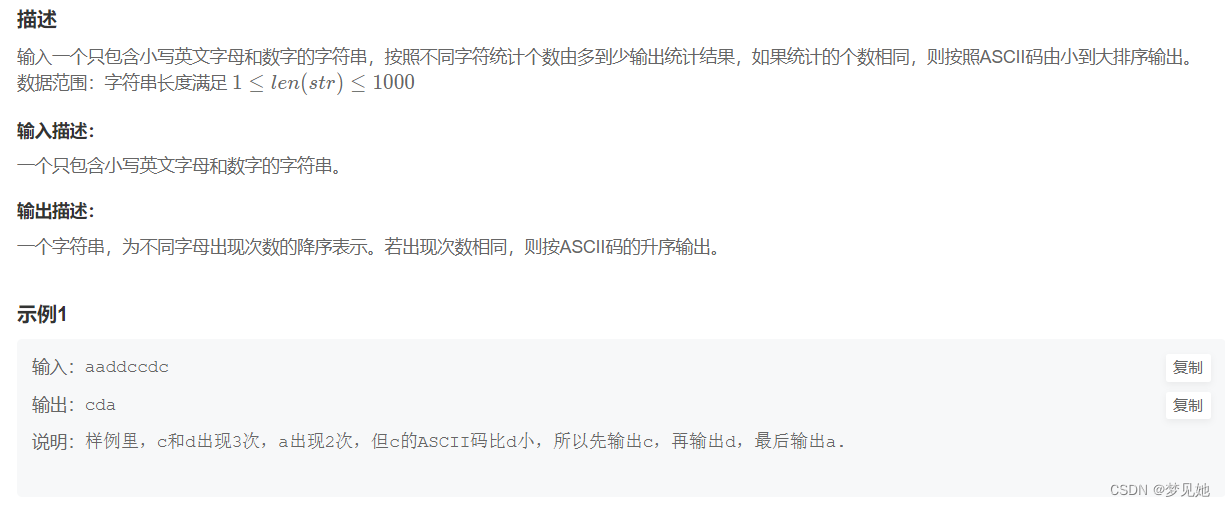
华为机考：HJ102 字符统计

华为机考&#xff1a;HJ102 字符统计 描述 方法1 先将所有字符计算数量&#xff0c;在对比其中字符的assic码 #include<iostream> #include<vector> #include<algorithm> #include<string> using namespace std; bool cmp(pair<char, int> a,…...

编程日记 2024/3/13 5:25:43

安装配置HBase

HBase集群需要整个集群所有节点安装的HBase版本保持一致&#xff0c;并且拥有相同的配置&#xff0c;具体配置步骤如下&#xff1a; 1. 解压缩HBase的压缩包 2. 配置HBase的环境变量 3. 修改HBase的配置文件&#xff0c;HBase的配置文件存放在HBase安装目录下的conf中 4. 首…...

编程日记 2024/3/13 5:24:42

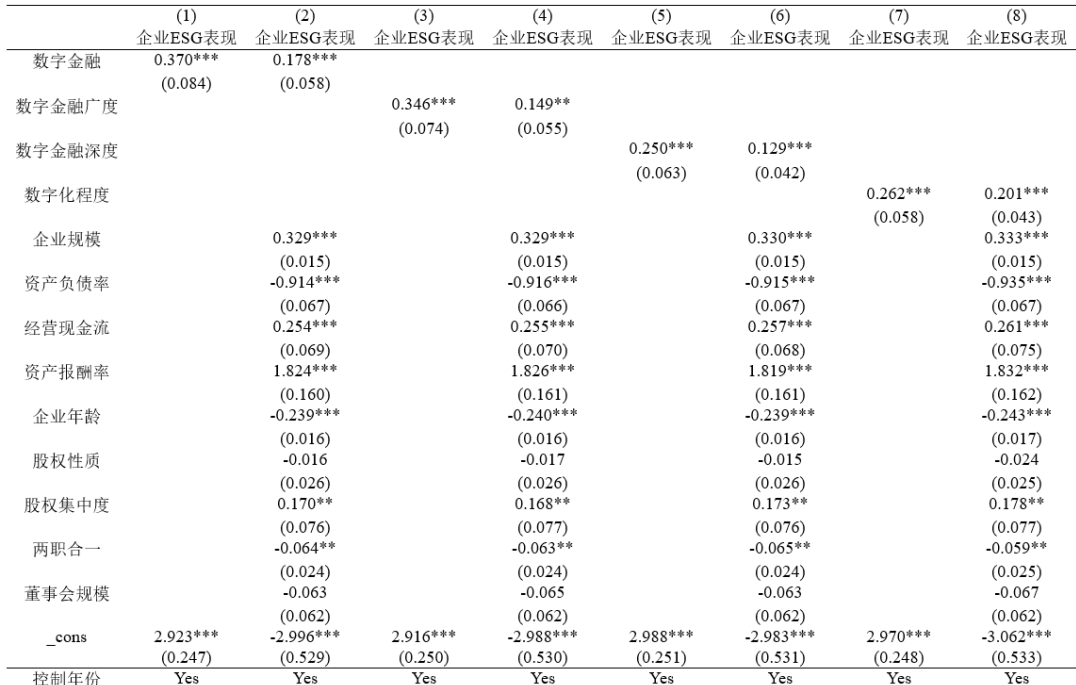
【更新】数字金融与企业ESG表现：效应、机制与“漂绿”检验数据集（2011-2022年）

参照温亚东&#xff08;2024&#xff09;的做法&#xff0c;本团队对来自统计与决策《数字金融与企业ESG表现&#xff1a;效应、机制与"漂绿"检验》一文中的基准回归部分进行复刻 一、数据介绍 数据名称&#xff1a;数字金融与企业ESG表现 参考期刊&#xff1a;《统…...

编程日记 2024/3/13 5:22:38

手写简易操作系统(五)--获得物理内存容量

前情提要 上一章中我们进入了保护模式&#xff0c;并且跳转到了32位模式下执行。这一章较为简单&#xff0c;我们来获取物理内存的实际容量。 一、获得内存容量的方式 在Linux中有多种方法获取内存容量&#xff0c;如果一种方法失败&#xff0c;就会试用其他方法。其本质上是…...

编程日记 2024/3/13 5:17:33

机器学习之DeepSequence软件使用学习3-预测突变效应

import theano import numpy as np import sys import pandas as pd import scipy #scipy 模块是 Python 中用于科学计算和数据分析的重要模块之一。它包含了许多高级的数学函数和工具&#xff0c;包括数值积分、优化、线性代数、统计等。 from scipy.stats import spearmanr #…...

编程日记 2024/3/13 5:15:32

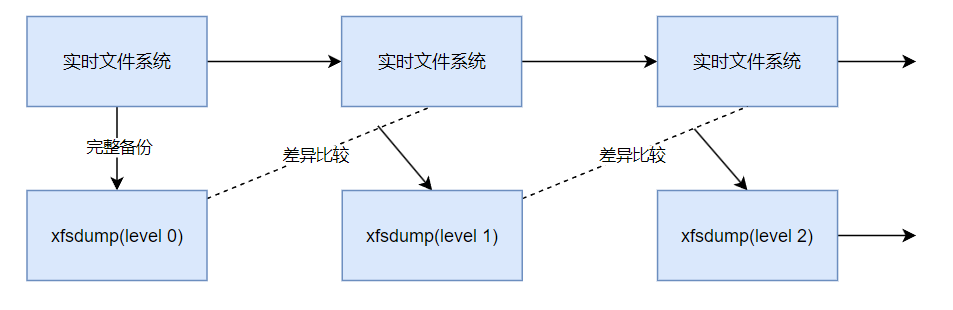
Linux文件与文件系统的压缩

文章目录 Linux文件与文件系统的压缩Linux系统常见的压缩命令gzip&#xff0c;zcat/zmore/zless/zgrepbzip2&#xff0c;bzcat/bzmore/bzless/bzgreppxz&#xff0c;xzcat/xzmore/xzless/xzgrepgzip&#xff0c;bzip2&#xff0c;xz压缩时间对比打包命令&#xff1a;tar打包命令…...

编程日记 2024/3/13 5:14:31

ubuntu 中进入python 编辑如何退出到命令行

文章目录 在Python解释器&#xff08;交互式命令行&#xff09;中&#xff0c;你可以使用 exit()函数或 CtrlD&#xff08;在Unix/Linux/macOS上&#xff09;或 CtrlZ然后输入 Enter&#xff08;在Windows上&#xff09;来退出Python解释器并返回到命令行。 以下是具体的步骤&a…...

编程日记 2024/3/13 5:10:27

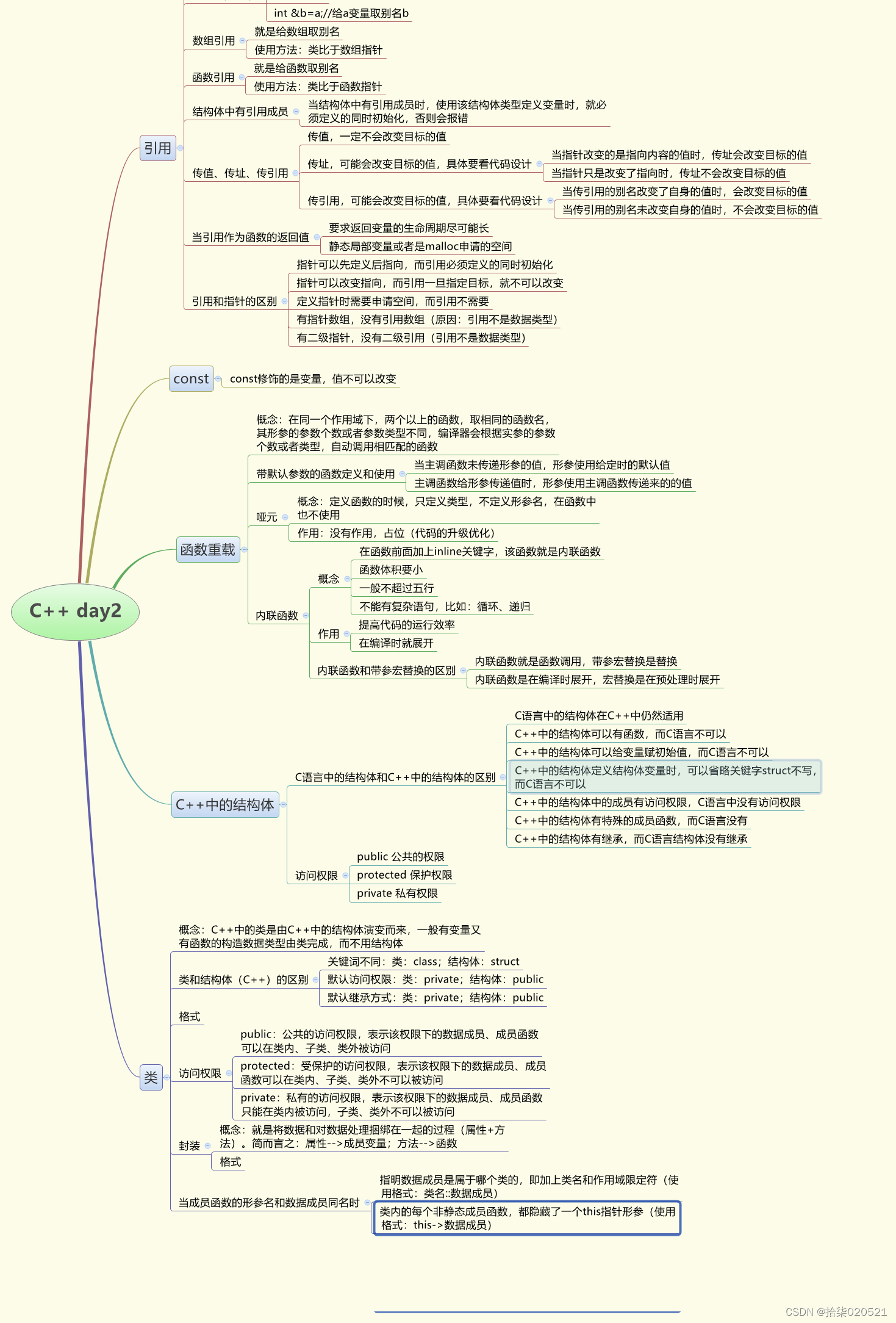
2024.3.12 C++

1.思维导图 2.自己封装一个矩形类(Rect)&#xff0c;拥有私有属性:宽度(width)、高度(height),定义公有成员函数: 初始化函数:void init(int w, int h)更改宽度的函数:set_w(int w)更改高度的函数:set_h(int h) 输出该矩形的周长和面积函数:void show() #include <iostream…...

编程日记 2024/3/13 5:05:22

飞塔防火墙开局百篇——002.FortiGate上网配置——透明模式配置（Transparent）

透明模式配置 开启透明模式创建策略 在不改变现有网络拓扑前提下&#xff0c;将防火墙NGFW以透明模式部署到网络中&#xff0c;放在路由器和交换机之间&#xff0c;防火墙为透明模式&#xff0c;对内网网段192.168.1.0/24的上网进行4~7层的安全防护。 登陆FortiGate防火墙界面&…...

编程日记 2024/3/13 4:56:13

代码随想录算法训练营第52天|300.最长递增子序列 674.最长连续递增序列 718.最长重复子数组

300.最长递增子序列 这道题还挺简单的&#xff0c;咱们设置dp[i]表示到第i个数字时的递增子序列的最长的值&#xff0c;那么dp[i]就要遍历从0到i-1的数&#xff0c;也就是看看当前这个数字是否比前面的数字大&#xff0c;如果大的话就看看现在的子序列长度是否会长于前面那个数…...

编程日记 2024/3/13 4:53:11

分享一些开源的游戏仓库

1.CnC_Remastered_Collection 红色警戒95版本 https://github.com/electronicarts/CnC_Remastered_Collection gitee仓库分流&#xff1a;https://gitee.com/loswdarmy/CnC_Remastered_Collection 2.Far-Cry-1-Source-Full 孤岛惊魂1 https://github.com/StrongPC123/Far-Cry-…...

编程日记 2024/3/13 4:52:10

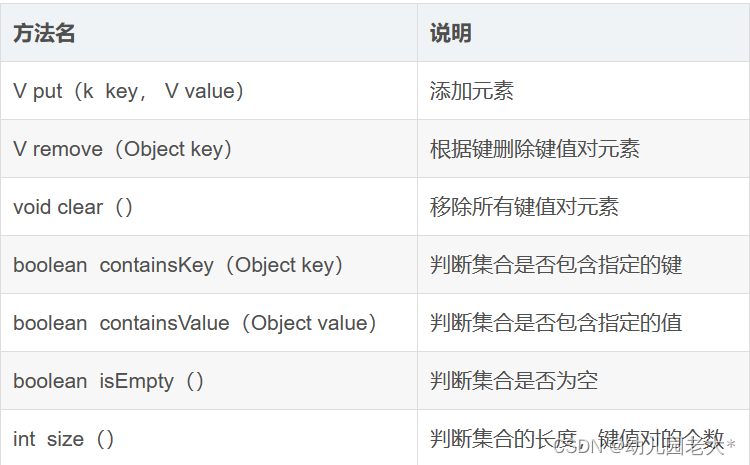
Java详解：单列 | 双列集合 | Collections类

○ 前言&#xff1a; 在开发实践中&#xff0c;我们需要一些能够动态增长长度的容器来保存我们的数据&#xff0c;java中为了解决数据存储单一的情况&#xff0c;java中就提供了不同结构的集合类&#xff0c;可以让我们根据不同的场景进行数据存储的选择&#xff0c;如Java中提…...

编程日记 2024/3/13 4:49:07

Centos7 使用docker来部署mondb

参考官方手册&#xff1a; https://www.mongodb.com/docs/manual/tutorial/install-mongodb-community-with-docker/#std-label-docker-mongodb-community-install 使用脚本快速安装docker curl -fsSL https://get.docker.com -o get-docker.sh | bash get-docker.sh使用 Doc…...

编程日记 2024/3/13 4:44:03

Java SE入门及基础（35）

接口 1. 概念 在软件工程中&#xff0c;软件与软件的交互很重要&#xff0c;这就需要一个约定。每个程序员都应该能够编写实现这样的约定。接口就是对约定的描述。 In the Java programming language, an interface is a reference type, similar to a class, that can con…...

编程日记 2024/3/13 4:43:02

基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的常见车型识别系统（Python+PySide6界面+训练代码）

摘要&#xff1a;本文深入探讨了如何应用深度学习技术开发一个先进的常见车型识别系统。该系统核心采用最新的YOLOv8算法&#xff0c;并与早期的YOLOv7、YOLOv6、YOLOv5等版本进行性能比较&#xff0c;主要评估指标包括mAP和F1 Score等。详细解析了YOLOv8的工作机制&#xff0c…...

编程日记 2024/3/13 4:42:01

Sqoop 学习

参考视频 大数据Sqoop教程丨从零开始讲解大数据业务及数据采集和迁移需求_哔哩哔哩_bilibili 介绍 Sqoop是Hadoop生态体系和RDBMS&#xff08;关系型数据库&#xff09;体系之间传送数据的一种工具 Hadop生态系统&#xff1a;HDFS&#xff0c;Hbase&#xff0c;Hive等 RDBMS包…...

编程日记 2024/3/13 4:41:00

Ollama 只安装 Ollama，本地快速部署谷歌开源大模型Gemma(基于Ollama)

参考&#xff1a;本地快速部署谷歌开源大模型Gemma(基于Ollama) - 知乎 确保系统更新: Bash sudo apt update && sudo apt upgrade 需要先下载Ollama&#xff0c;版本要求0.1.26及以上 运行curl -fsSL https://ollama.com/install.sh | sh 监听 Ollama API 接…...

编程日记 2024/3/13 4:34:55

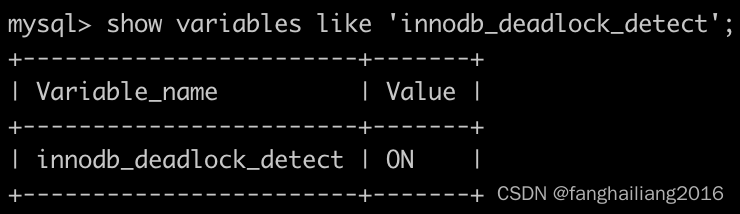
一条 sql 语句可能导致的表锁和行锁以及死锁检测

锁 MDL 当对一个表做增删改查操作的时候&#xff0c;加 MDL 读锁&#xff1b;当要对表做结构变更操作的时候&#xff0c;加 MDL 写锁 ALTER TABLE tbl_name NOWAIT add column ... ALTER TABLE tbl_name WAIT N add column ... …...

编程日记 2024/3/13 4:33:54

prometheus 原理（架构，promql表达式，描点原理）

大家好&#xff0c;我是蓝胖子&#xff0c;提到监控指标&#xff0c;不得不说prometheus&#xff0c;今天这篇文章我会对prometheus 的架构设计&#xff0c;promql表达式原理和监控图表的绘图原理进行详细的解释。来让大家对prometheus的理解更加深刻。 架构设计 先来看看&am…...

编程日记 2024/3/13 4:32:51

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)

题目&#xff1a;3442. 奇偶频次间的最大差值 I 思路 &#xff1a;哈希&#xff0c;时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况&#xff0c;哈希表这里用数组即可实现。 C版本&#xff1a; class Solution { public:int maxDifference(string s) {int a[26]…...

编程新知 2026/2/7 23:18:31

Leetcode 3576. Transform Array to All Equal Elements

Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接&#xff1a;3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到&#xf…...

编程新知 2025/9/17 7:25:07

Zustand 状态管理库：极简而强大的解决方案

Zustand 是一个轻量级、快速和可扩展的状态管理库&#xff0c;特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

编程新知 2026/2/8 10:56:57

家政维修平台实战20：权限设计

目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系&#xff0c;主要是分成几个表&#xff0c;用户表我们是记录用户的基础信息&#xff0c;包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题&#xff0c;不同的角色&#xf…...

编程新知 2026/2/1 22:23:58

第 86 场周赛：矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词

Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵&#xff0c;其中每行&#xff0c;每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid&#xff0c;其中有多少个 3 3 的 “幻方” 子矩阵&am…...

编程新知 2026/2/7 13:27:36

django blank 与 null的区别

1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是&#xff0c;要注意以下几点&#xff1a; Django的表单验证与null无关&#xff1a;null参数控制的是数据库层面字段是否可以为NULL&#xff0c;而blank参数控制的是Django表单验证时字…...

编程新知 2025/7/7 3:34:13

Qt 事件处理中 return 的深入解析

Qt 事件处理中 return 的深入解析 在 Qt 事件处理中&#xff0c;return 语句的使用是另一个关键概念&#xff0c;它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别&#xff1a;不同层级的事件处理 方…...

编程新知 2025/6/10 21:19:52

抽象类和接口（全）

一、抽象类 1.概念&#xff1a;如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象&#xff0c;这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法&#xff0c;包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中&#xff0c;⼀个类如果被 abs…...

编程新知 2026/2/5 4:38:22

Python 训练营打卡 Day 47

注意力热力图可视化 在day 46代码的基础上&#xff0c;对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

编程新知 2025/11/24 9:42:16

mac：大模型系列测试

0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何&#xff0c;是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试&#xff0c;是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

编程新知 2026/2/4 0:46:21