3.12练习题解
1.台阶问题:

这道题目一看其实很容易想到可以用dp的板子去做,并且只需要用一维dp即可,其中dp的下标表示到达当前阶梯总共有多少种方法,由于结果有可能会很大所以一定要记得边记录边模,代码实现如下:
#include<bits/stdc++.h>
using namespace std;
const int mod = 100003;
int n,k;
int dp[100010];
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin>>n>>k;dp[0]=dp[1]=1;for(int i=2;i<=n;i++){for(int j=1;j<=k;j++){if(i>=j){dp[i]=(dp[i]+dp[i-j]) % mod;} }}cout<<dp[n]%mod;return 0;
}2.递增三元组:

这一道题目的意思是比较好理解的,我们需要考虑的是,由于给的N的极限值是1e5,所以暴力的方式时间复杂度n的三方肯定会爆,于是我们就要考虑如何对时间复杂度进行优化。
我们可以这样进行考虑,由于数组b是中间数组,我们不妨先对三个数组进行排序,然后我们对b进行枚举,对于每一次枚举,我们在a数组中找到所有小于当前枚举对应的b数组下标元素的个数,然后再找到c数组中所有大于当前b数组下标所对应的元素个数,再把当前符合条件的总个数加到ans上面即可。
再继续思考我们对于每次枚举,然后在a,c数组中查找符合要求的,都可以通过二分进行查找从而降低时间复杂度。所以代码如下:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;typedef long long LL;
const int N = 1e5+10;
int num[3][N];int main() {int n;scanf("%d", &n);for(int i = 0; i < 3; ++i) for(int j = 1; j <= n; ++j) scanf("%d", &num[i][j]);for(int i = 0; i < 3; ++i)sort(num[i]+1, num[i]+n+1);LL ans = 0;//枚举B,寻找A满足的个数以及C满足的个数相乘for(int i = 1; i <= n; ++i) {int key = num[1][i];//A中二分查找第一个不小于key的数的下标int pos1 = lower_bound(num[0]+1, num[0]+n+1, key)-num[0]-1;//C中二分查找第一个大于key的数的下标int pos2 = upper_bound(num[2]+1, num[2]+n+1, key)-num[2];if(pos1 >= 1 && pos2 <= n) {ans += (LL)pos1*(n-pos2+1);}}cout<<ans<<endl;return 0;
}
这段代码有需要解释的地方:
num[0]+1:这是指向num数组的第一个元素的下一个位置的指针。换句话说,它指向num数组中的第二个元素。num[0]+n+1:这是指向num数组的最后一个元素的下一个位置的指针。换句话说,它指向num数组之后的第一个位置。lower_bound(num[0]+1, num[0]+n+1, key):这是在num数组的第二个元素和最后一个元素之间(不包括最后一个元素)查找第一个不小于key的元素的迭代器。lower_bound(...)-num[0]-1:这将返回的迭代器与num数组的第一个元素的指针相减,然后减去1。这样,我们得到的是找到的元素在num数组中的索引。
所以,pos1存储的是key在num数组中的位置,如果key不在num数组中,则pos1将是key应该插入的位置,以保持num数组的有序性。
简而言之,这段代码在num数组中查找key的位置,并返回其索引。如果key不在数组中,则返回应该插入key的位置。
在C++中,指针的算术运算实际上是对指针所指向的内存地址进行算术运算。当两个指针指向同一个数组或同一个对象的成员时,它们之间的差值表示两个元素之间的偏移量,这个偏移量是以元素为单位,而不是以字节为单位。
对于数组num,num[0]是一个指向数组第一个元素的指针。当我们执行lower_bound函数时,得到的是一个迭代器,它指向数组中第一个不小于key的元素。这个迭代器也是一个指针,指向数组中的某个元素。
当从lower_bound返回的迭代器中减去num[0]时,得到的是两个指针之间的偏移量,这个偏移量表示从数组的第一个元素到找到的元素之间有多少个元素。因为lower_bound返回的迭代器指向的是数组中的元素,而不是元素之间的空隙,所以这个偏移量实际上就是找到的元素在数组中的下标(从0开始计数)。
最后,减去1,是因为我们希望得到的是下标而不是偏移量。在C++中,数组的下标是从0开始的,而指针的偏移量是从1开始的(即,指向第一个元素的指针偏移量为0,指向第二个元素的指针偏移量为1,依此类推)。因此,减去1将偏移量转换为正确的下标。
所以,lower_bound(...)-num[0]-1的结果就是找到的元素在数组中的下标。
第二种方法:双指针优化:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;typedef long long LL;
const int N = 1e5+10;
int num[3][N];int main() {int n;scanf("%d", &n);for(int i = 0; i < 3; ++i) for(int j = 1; j <= n; ++j) scanf("%d", &num[i][j]);for(int i = 0; i < 3; ++i)sort(num[i]+1, num[i]+n+1);LL ans = 0;//枚举B,寻找A满足的个数以及C满足的个数相乘int a = 1, c = 1;for(int i = 1; i <= n; ++i) {int key = num[1][i];while(a<=n && num[0][a] < key) a++;while(c<=n && num[2][c] <= key) c++;ans += (LL)(a-1)*(n-c+1);}cout<<ans<<endl;return 0;
}其实也就是将二分中的部分更改了一下。
之前的双指针算法时间复杂度的瓶颈为:排序O(nlog2n)
考虑是否可以不排序在O(n)的时间内解决此问题呢?
既然要排序实现快速的查找A中小于B[i]的数的个数,可以将数组A中所有元素出现的次数存入一个哈希表中,因为数组中元素的范围只有n5, 可以开一个大的数组cnta 作为哈希表。
在枚举B中元素时,我们需要快速查找找小于B[i]的所有元素的总数,只需要在枚举之前先将求出表中各数的前缀和即可。
查找C与查找A同理可得。
代码如下:
//前缀和
#include <iostream>
#include <cstdio>using namespace std;typedef long long LL;
const int N = 1e5+10;
int A[N], B[N], C[N];
int cnta[N], cntc[N], sa[N], sc[N];int main() {int n;scanf("%d", &n);//获取数i在A中有cntc[i]个,并对cnt求前缀和safor(int i = 1; i <= n; ++i) {scanf("%d", &A[i]);cnta[++A[i]]++;}sa[0] = cnta[0];for(int i = 1; i < N; ++i) sa[i] = sa[i-1]+cnta[i];//B只读取即可for(int i = 1; i <= n; ++i) scanf("%d", &B[i]), B[i]++;//获取数i在C中有cntc[i]个,并对cnt求前缀和scfor(int i = 1; i <= n; ++i) {scanf("%d", &C[i]);cntc[++C[i]]++;}sc[0] = cntc[0];for(int i = 1; i < N; ++i) sc[i] = sc[i-1]+cntc[i]; //遍历B求解LL ans = 0;for(int i = 1; i <= n; ++i) {int b = B[i];ans += (LL)sa[b-1] * (sc[N-1] - sc[b]);}cout<<ans<<endl;return 0;
}感谢您的观看。
相关文章:

3.12练习题解
1.台阶问题: 这道题目一看其实很容易想到可以用dp的板子去做,并且只需要用一维dp即可,其中dp的下标表示到达当前阶梯总共有多少种方法,由于结果有可能会很大所以一定要记得边记录边模,代码实现如下: #incl…...

Java中实现双向链表
一、目标 最近项目中实现双向链表,同时转为满二叉树。 二、代码 用java实现双向链表的代码如下: class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) { val x; } }public class FullBinaryTree {public TreeNode createTree(int[…...

【DevOps实战之k8s】使用Prometheus和Grafana监控K8S集群
【DevOps实战之k8s】使用Prometheus和Grafana监控K8S集群 目录 【DevOps实战之k8s】使用Prometheus和Grafana监控K8S集群系统架构Kubernetes集群指标抓取指标可视化警告PromQL示例按命名空间统计集群中的Pod数按命名空间重启Pod未就绪的PodCPU过度使用Memory过度使用健康的集群…...

【读论文】【精读】3D Gaussian Splatting for Real-Time Radiance Field Rendering
文章目录 1. What:2. Why:3. How:3.1 Real-time rendering3.2 Adaptive Control of Gaussians3.3 Differentiable 3D Gaussian splatting 4. Self-thoughts 1. What: What kind of thing is this article going to do (from the a…...
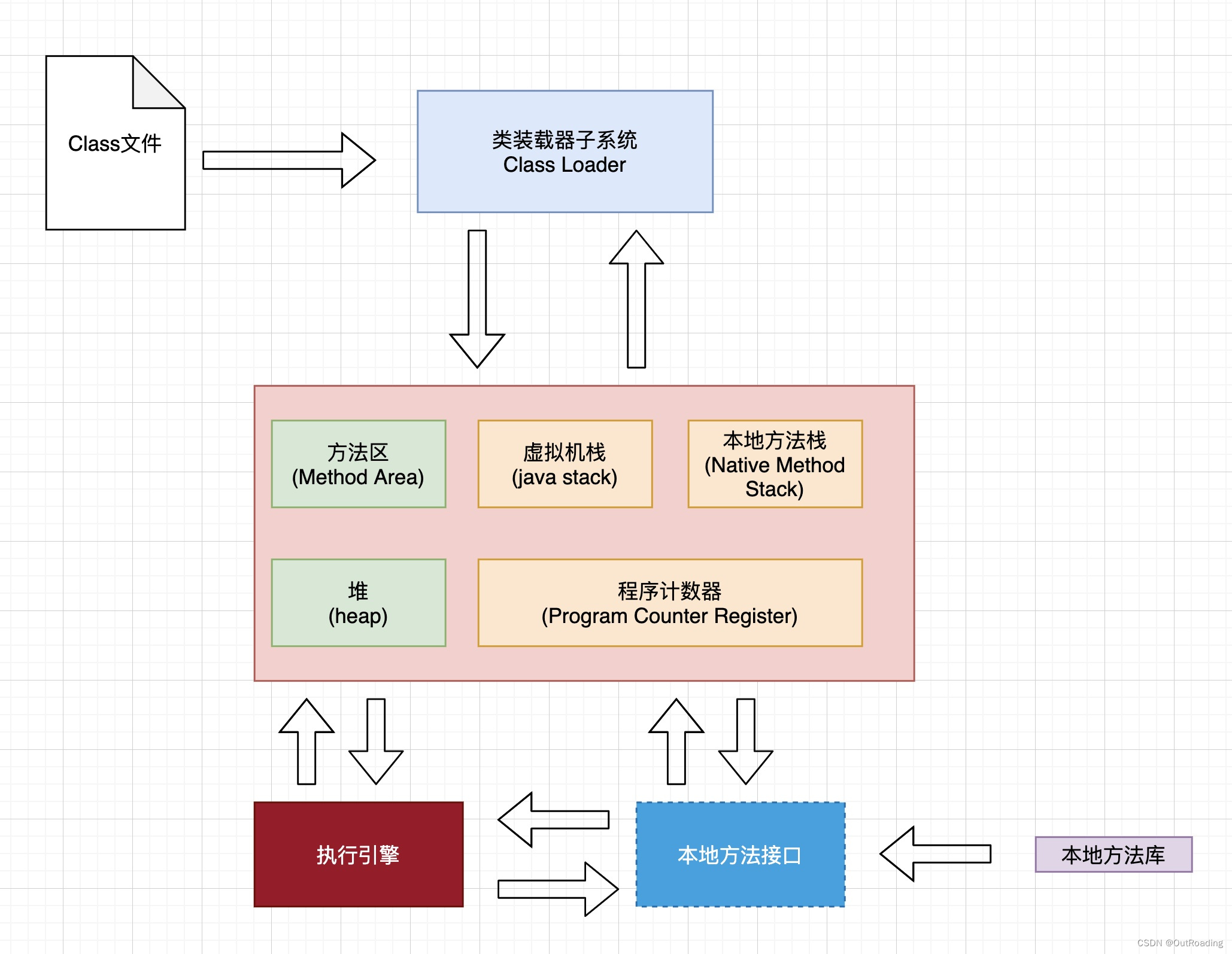
JVM理解学习
参考视频 JVM架构总览图 程序计数器 程序计数器,物理上用寄存器实现。 作用: 记住下一条JVM指令的执行地址 特点: 1 是线程私有的,随着线程的创建而创建,随着线程的消息而消息 2 是一小块内存 3 唯一不会内存溢出的地方…...

使用 Ruby 或 Python 在文件中查找
对于经常使用爬虫的我来说,在大多数文本编辑器都会有“在文件中查找”功能,主要是方便快捷的查找自己说需要的内容,那我有咩有可能用Ruby 或 Python实现类似的查找功能?这些功能又能怎么实现? 问题背景 许多流行的文本…...

python实现冒泡排序
冒泡排序是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。 以下是用Python实现冒泡排序的代…...
)
大数据开发(HBase面试真题-卷二)
大数据开发(HBase面试真题) 1、HBase读写数据流程?2、HBase的读写缓存?3、在删除HBase中的一个数据的时候,它什么时候真正的进行删除呢?4、HBase的一个region由哪些东西组成?5、HBase的rowkey为…...
基于springboot+vue的线上教育系统(源码+论文)
目录 前言 一、功能设计 二、功能实现 三、库表设计 四、论文 前言 现在大家的生活方式正在被计算机的发展慢慢改变着,学习方式也逐渐由书本走向荧幕,我认为这并不是不能避免的,但说实话,现在的生活方式与以往相比有太大的改变,人们的娱乐方式不仅仅…...

01-shell的自学课-基础变量学习
一、echo变量的一个坑 声明【临时变量】,然后打印出来;(拓展:env是linux的全局变量) [rootgong ~]# xinjizhiwashell [rootgong ~]# echo $xinjizhiwa shell [rootgong ~]# echo $xinjizhiwa-haha shell-haha [rootgo…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Span)
作为Text组件的子组件,用于显示行内文本的组件。 说明: 该组件从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 该组件从API Version 10开始支持继承父组件Text的属性,即如果子组件未设置…...

前端框架的演进之路:从静态网页到现代交互体验的探索
前端框架的发展史 随着互联网的快速发展,前端技术也在不断进步,前端框架作为前端开发的重要工具,经历了从简单到复杂、从单一到多元的演变过程。本文将回顾前端框架的发展史,探讨其变迁背后的原因和趋势。 一、静态网页时代 在…...

在Linux/Ubuntu/Debian中设置字体
下载字体。 下载你喜欢的字体,双击并安装。 之后更新字体缓存: fc-cache -f -v安装 GNOME 调整。 GNOME Tweaks 是一个工具,允许你自定义 GNOME 桌面环境的各个方面,包括字体。 如果你还没有安装 GNOME Tweaks: …...

Python 常用内置函数,及实例演示
Python的内置函数非常强大,可以帮助你完成各种任务。以下是20个非常有用的Python内置函数及其使用实例: 1. abs() 返回数字的绝对值。 print(abs(-5)) # 输出:52. all() 如果迭代器的所有元素都为真(或迭代器为空)…...

C++标准输入输出和名字空间
C标准输入输出和名字空间 标准输入输出 在C中,标准输入输出(I/O)是通过标准库中的iostream库来实现的,它提供了一套流(stream)抽象来进行数据的输入和输出操作。这套流抽象包括输入流用于读取数据&#x…...

hive逗号分割行列转换
select * from ( select back_receipt_nos,order_no,reject_no from ods_oneplus.ods_us_wms_reject_order_match_all_d where order_no 10150501385980001 ) t1 lateral view explode(split(t1.back_receipt_nos, ,)) t as back_receipt_no where 1 1;...
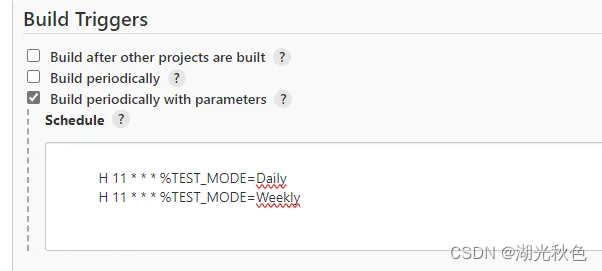
Jenkins插件Parameterized Scheduler用法
Jenkins定时触发构建的同时设定参数。可以根据不同的定时构建器设置不同参数或环境变量的值。可以设置多个参数。并结合when控制stage流程的执行。结合when和triggeredBy区分定时构建的stage和手动执行的stage。 目录 什么是Parameterized Scheduler?如何配置实现呢…...

西门子S7.NET通信库【读】操作详解
在使用西门子PLC进行工业自动化控制的过程中,经常需要与PLC进行数据交换。S7.NET是一款广泛应用于.NET平台的西门子PLC通信库,它为开发者提供了一系列的API函数,以便在C#、VB.NET等.NET语言中轻松实现与西门子PLC的数据交互。本文将详细介绍如…...

Qt/C++音视频开发69-保存监控pcm音频数据到mp4文件/监控录像/录像存储和回放/264/265/aac/pcm等
一、前言 用ffmpeg做音视频保存到mp4文件,都会遇到一个问题,尤其是在视频监控行业,就是监控摄像头设置的音频是PCM/G711A/G711U,解码后对应的格式是pcm_s16be/pcm_alaw/pcm_mulaw,将这个原始的音频流保存到mp4文件是会…...

闲聊Swift的枚举关联值
闲聊Swift的枚举关联值 枚举,字面上理解,就是把东西一件件列出来。 在许多计算机语言中,枚举都是一种重要的数据结构。使用枚举可以使代码更简洁,语义性更强,更加健壮。 Swift语言也不例外。但和其他语言相比…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
