20240312-2-贪心算法
贪心算法

是每次只考虑当前最优,目标证明每次是考虑当前最优能够达到局部最优,这就是贪心的思想,一般情况下贪心和排序一起出现,都是先根据条件进行排序,之后基于贪心策略得到最优结果。
面试的时候面试官一般不会出贪心算法,如果可能贪心一般都可以使用动态规划解决,面试官很喜欢出动态规划的题目。
1. 最大连续子序列
题目: 给定一个整数数组,找到一个具有最大和的子数组,返回其最大和。
扩展1: 给定一个整数数组,找出两个 不重叠 子数组使得它们的和最大。
扩展2: 给定一个整数数组,找出两个不重叠的子数组A和B,使两个子数组和的差的绝对值|SUM(A) - SUM(B)|最大。
分析: 使用这个s表示当前可能满足的最大和,如果s>0,我们认为s对接下来的加操作有帮助,基于s+=nums[i],if s < 0, 认为s只会对后面造成负影响,两s=nums[i]。
扩展问题: 可以将 数组从每个位置k分开,分别结算[1,i]和[i+1, n)的最值,记录的过程中可以使用数组保存下来的已经计算好的值。
int maxSubArray(vector<int> &nums) {int s = 0, ans = -1000000;for(int i = 0; i < nums.size(); i ++) {if(s > 0) s += nums[i];else s = nums[i];ans = max(s, ans);}return ans;
}
2. 删除数字
题目: 给定一个以字符串表示的非负整数,从该数字中移除掉k个数位,让剩余数位组成的数字尽可能小,求可能的最小结果。
分析: 从左到右遍历字符串,找到第一个不满足递增的数字删除,一定会保证当前操作之后剩下的数字最小。
string removeKdigits(string &num, int k) {int i;while(k --) {for(i = 0; i < num.size() - 1 && num[i] <= num[i+1]; i ++);num.erase(num.begin() + i);}// remove 0auto it = num.begin();while(it != num.end() && *it == '0') {num.erase(it);it = num.begin();}if(num.size() == 0) num = "0";return num;
}3. 无重叠区间
题目: 给定一些区间,找到需要移除的最小区间数,以使其余的区间不重叠。
分析: 贪心一般伴随着排序一起出现,我们根据区间的结束使用升序排序,之后进行遍历,如果发现不满足条件,则移除这个不满足的区间。
classs Interval {int start, end;Interval(int start, int end) {this->start = start;this->end = end;}
}
bool cmp(Interval a, Interval b) {if(a.end < b.end) return 1;else return 0;
}
int eraseOverlapIntervals(vector<Interval> &intervals) {sort(intervals.begin(), intervals.end(), cmp); int cnt = 0;Interval tmp = intervals[0];for(int i = 1; i < intervals.size(); i ++) {if(tmp.end <= intervals[i].start) tmp = intervals[i];else {cnt ++;}}return cnt;
}
4. 合并数字
题目: 给出n个数,现在要将这n个数合并成一个数,每次只能选择两个数a,b合并,每次合并需要消耗a+b的能量,输出将这n个数合并成一个数后消耗的最小能量。
分析: 参考哈夫曼树的构造,每一次合并两个最小的数,直到剩下一个数字,因为每次要选择两个最小的,需要用到最小堆来实现,可以使用C++SLT中的优先队列.
根据这个题目,请大家自行补上哈夫曼树。
int mergeNumber(vector<int> &numbers) {priority_queue<int, vector<int>, greater<int>> pq;for(int i = 0; i < numbers.size(); i ++) {pq.push(numbers[i]);}int cost = 0;while(pq.size() > 1) {int a = pq.top();pq.pop();int b = pq.top();pq.pop();cost += (a + b);pq.push(a + b);}return cost;
}5. 最小支撑树
题目: 使用kruskal算法,构造最小支撑树。
分析: 详见百度百科或者wikipedia.
代码: kruskal code
struct Edge { int src, dest, weight;
};
struct Graph { int V, E; struct Edge* edge;
};
struct Graph* createGraph(int V, int E) { struct Graph* graph = new Graph; graph->V = V; graph->E = E; graph->edge = new Edge[E]; return graph;
}
struct subset { int parent; int rank;
};
int find(struct subset subsets[], int i) { if (subsets[i].parent != i) subsets[i].parent = find(subsets, subsets[i].parent); return subsets[i].parent;
}
void Union(struct subset subsets[], int x, int y) { int xroot = find(subsets, x); int yroot = find(subsets, y); if (subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot; else if (subsets[xroot].rank > subsets[yroot].rank) subsets[yroot].parent = xroot; else { subsets[yroot].parent = xroot; subsets[xroot].rank++; }
}
int myComp(const void* a, const void* b) { struct Edge* a1 = (struct Edge*)a; struct Edge* b1 = (struct Edge*)b; return a1->weight > b1->weight;
}
void KruskalMST(struct Graph* graph) { int V = graph->V; struct Edge result[V]; int e = 0; int i = 0; qsort(graph->edge, graph->E, sizeof(graph->edge[0]), myComp); struct subset *subsets = (struct subset*) malloc( V * sizeof(struct subset) ); for (int v = 0; v < V; ++v) { subsets[v].parent = v; subsets[v].rank = 0; } while (e < V - 1) { struct Edge next_edge = graph->edge[i++]; int x = find(subsets, next_edge.src); int y = find(subsets, next_edge.dest); if (x != y) { result[e++] = next_edge; Union(subsets, x, y); } } return;
}
6. 补齐数组
题目: 给出一个正整数数组nums和一个整数n,向数组添加patch元素,使得范围[1, n]包含的任何数字都可以由数组中某些元素的总和形成。返回所需的最少补齐数。
分析:
- 升序排序,
- 使用r表示目前可以表示的右边界,如果当前值 > r, 超出范围,又因为 [1, n] 区间内的任何数字都可以用 nums 中某几个数字的和来表示,那么只需要有n/2以及 [1, n/2] 区间内任何数字都可以用 nums 中某几个数字的和来表示即可。所有我们将r扩大一倍,继续判断是否满足。
- 直到 r >= n。
int minPatches(vector<int> &nums, int n) {sort(nums.begin(), nums.end());long long r = 1;int i = 0;int cnt = 0;while(r <= n) {if(i < nums.size() && nums[i] <= r) r += nums[i++];else {cnt ++;r *= 2;}}return cnt;
}
7. 买卖股票的最佳时机
题目: 假设有一个数组,它的第i个元素是一支给定的股票在第i天的价格。如果你最多只允许完成一次交易(例如,一次买卖股票),设计一个算法来找出最大利润。
分析: 先低价买入,再高价卖出,因此从前向后,记录最小值并且更新最有结果,
int maxProfit(vector<int> &prices) {int minp = prices[0];int ans = 0;for(int i = 1; i < prices.size(); i ++) {ans = max(ans, prices[i] - minp);minp = min(minp, prices[i]);}return ans;
}
8. 买卖股票的最佳时机II
题目: 假设有一个数组,它的第i个元素是一个给定的股票在第i天的价格。设计一个算法来找到最大的利润。你可以完成尽可能多的交易(多次买卖股票)。然而,你不能同时参与多个交易(你必须在再次购买前出售股票)。
分析: 多次买卖,我们可以尽可能多的买卖股票,如果满足prices[i+1] > price[i],就进行一次买卖,其实我们知道如果是一个递增序列,(prices[i+1] - prices[i]) + (prices[i] - prices[i-1]) = prices[i+1] - prices[i],可以保证我们将所有可能的买卖识别出来。
int maxProfit(vector<int> &prices) {int sum = 0;for(int i=1;i<prices.size();i++){if(prices[i] > prices[i-1]){sum += prices[i] - prices[i-1];}}return sum;
}
9. 买卖股票的最佳时机含手续费
题目: 给定一个数组,其中第i个元素是一支股票在第i天的价格,以及一个非负数 fee 代表了交易手续费。(只需要在卖出时支付 fee)。你可以进行任意次交易,而每次交易都必须付手续费,而且你不能持有超过1支数量的股票(也就是说,你在买入之前需要先把之前买入的卖出)。返回可以获得的最大利润。
分析:
- 我们考虑最朴素的方法,对于每一天,如果当前有股票,考虑出售或者保留,如果没股票,考虑购买或者跳过,进行dfs搜索。每天都有两种操作,时间复杂度为O(2^n).
- 如何优化呢?我们用动态规划的思想来解决这个问题,考虑每一天同时维护两种状态:拥有股票(own)状态和已经售出股票(sell)状态。用own和sell分别保留这两种状态到目前为止所拥有的最大利润。 对于sell,用前一天own状态转移,比较卖出持有股是否能得到更多的利润,即sell = max(sell , own + price - fee), 而对于own , 我们考虑是否买新的股票更能赚钱(换言之,更优惠),own=max( own, sell-price).
- 初始化我们要把sell设为0表示最初是sell状态且没有profit,把own设为负无穷因为最初不存在该状态,我们不希望从这个状态进行转移.
- 因为我们保存的都是最优状态,所以在买卖股票时候取max能保证最优性不变.
- 最后直接返回sell即可.
- 来自(https://www.jiuzhang.com/solution/best-time-to-buy-and-sell-stock-with-transaction-fee/#tag-highlight-lang-cpp)
int maxProfit(vector<int> &prices, int fee) {int sell = 0, buy = -prices[0];for (int price : prices) {int sellOld = sell;sell = max(sell, buy + price - fee);buy = max(buy, sellOld - price);}return sell;
}
10. 最后的猫
题目: 给你一个n只猫,每一个猫都有一个初始化的萌系数,当一只猫的萌系数变成0它就会离开你。现在你实在受不了这n只萌猫,想要只留下一只猫,并且使它的萌系数最低。每一个你可以选择任意一只猫A去消耗另外一只猫B的萌系数,这样的话猫B的萌系数就会减去猫A的萌系数,当猫A的萌系数不变。通过多次回合之后,最后剩下的猫的萌系数最小是多少。
分析: 我们的目的是留下一只猫,使它的萌系数最小,从这个角度出发,我们可以选择最小萌系数的猫,去消耗其他的猫,如果其他的猫萌系数变成0,就离开了。例如最小萌系数的猫的系数是a,对于其他的猫,如果b%a == 0,则经过多次消耗之后,b就会离开,如果b%a!=0, 则结果是经过多轮消耗之后变成(b%a, a),直到一方变成0,我们可以发现这是一个求最大公约的算式。因此,最后的猫萌系数是gcd(h[0],h[0],…,h[n-1]);
int gcd(int a, int b) {if(a == 0) return b;return gcd(b % a, a);
}
int solve(vector<int> &h) {if(h.size() == 1) return h[0];int ans = gcd(h[0], h[1]);for(int i = 2; i < h.size(); i ++) {ans = gcd(ans, h[i]);}return ans;
}
相关文章:

20240312-2-贪心算法
贪心算法 是每次只考虑当前最优,目标证明每次是考虑当前最优能够达到局部最优,这就是贪心的思想,一般情况下贪心和排序一起出现,都是先根据条件进行排序,之后基于贪心策略得到最优结果。 面试的时候面试官一般不会出贪…...

前端 --- HTML
1. HTML 结构 1.1 HTML 文件基本结构 <html><head><title>第一个html程序</title></head><body>hello world!</body> </html> html 标签是整个 html 文件的根标签(最顶层标签)head 标签中写页面的属性.body 标签中写的是页…...

curl c++ 实现HTTP GET和POST请求
环境配置 curl //DV2020T环境下此步骤可省略 https://curl.se/download/ 笔者安装为7.85.0版本 ./configure --without-ssl make sudo make install sudo rm /usr/local/lib/curl 系统也有curl库,为防止冲突,删去编译好的curl库。 对以json数据的解析使…...
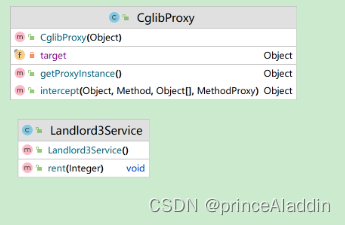
12、设计模式之代理模式(Proxy)
一、什么是代理模式 代理模式属于结构型设计模式。为其他对象提供一种代理以控制对这个对象的访问。 在某些情况下,一个对象不适合或者不能直接引用另一个对象,而代理对象可以在客户端和目标对象之间起到中介的作用。 二、分类 代理模式分为三类&#…...

springboot集成Quartz定时任务组件
文章目录 前言一、Quartz 是什么?下面是对 Java 中 Quartz 的主要概念的简单描述: 二、使用步骤总结 前言 平时开发中相信大家都经常用到定时任务吧,最近简单的就是直接使用Scheduled注解标注到方法上用注解的方式在项目运行时无法去对任务进…...

代码随想录算法训练营第38天—动态规划06 | ● 完全背包 ● *518. 零钱兑换 II ● 377. 组合总和 Ⅳ
完全背包 视频讲解:https://www.bilibili.com/video/BV1uK411o7c9 https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85.html 题目描述:有n件物品和一个最多能…...
复写零)
C语言每日一题(63)复写零
题目链接 力扣网 1089 复写零 题目描述 给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。 注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改,不…...

ElasticSearch聚合查询
数据准备 索引创建 PUT product {"mappings": {"properties": {"createtime": {"type": "date"},"desc": {"type": "text","fields": {"keyword": {"type": …...
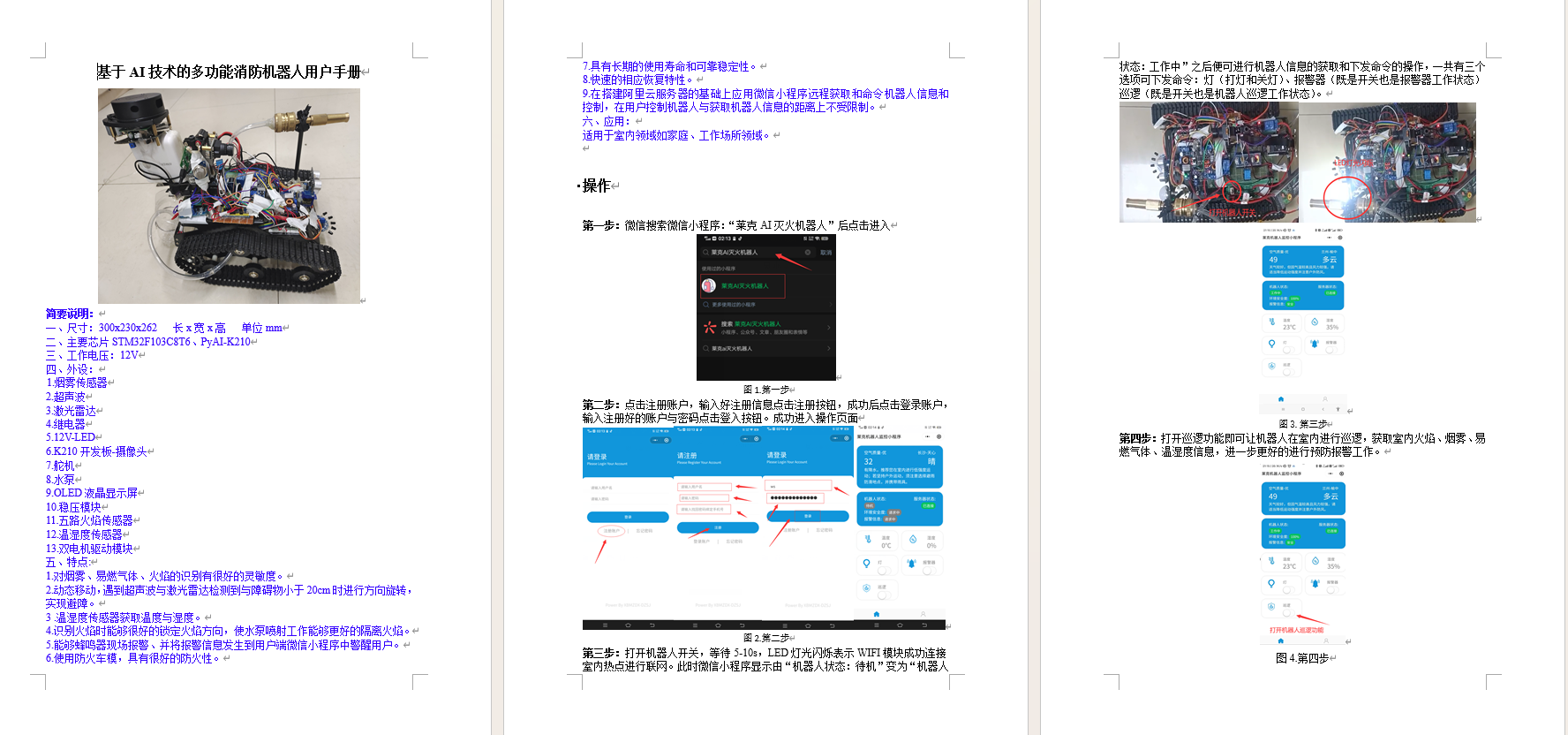
【毕设级项目】基于AI技术的多功能消防机器人(完整工程资料源码)
基于AI技术的多功能消防机器人演示效果 竞赛-基于AI技术的多功能消防机器人视频演示 前言: 随着“自动化、智能化”成为数字时代发展的关键词,机器人逐步成为社会经济发展的重要主体之一,“机器换人”成为发展的全新趋势和时代潮流。在可预见…...
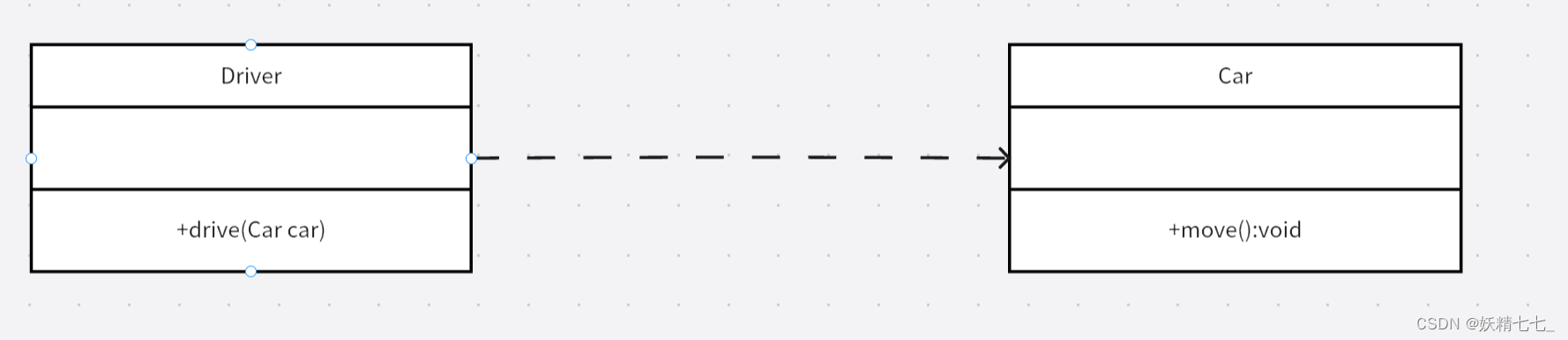
【一】【设计模式】类关系UML图
1. 继承(Generalization) 继承是对象间的一种层次关系,允许子类继承并扩展父类的功能。 UML线:带有空心箭头的直线,箭头指向基类(父类)。 class Parent {public void parentMethod() {System.…...

【DevOps基础篇】容器化架构基础设施监控方案
【DevOps基础篇】容器化架构基础设施监控方案 目录 【DevOps基础篇】容器化架构基础设施监控方案要监视什么不同监控系统方案比较1. Datadog2. Prometheus3. ELK(Elasticsearch、Logstash、Kibana)4. Sysdig5. 自行打造!如何选择总结推荐超级课程: Docker快速入门到精通 当…...
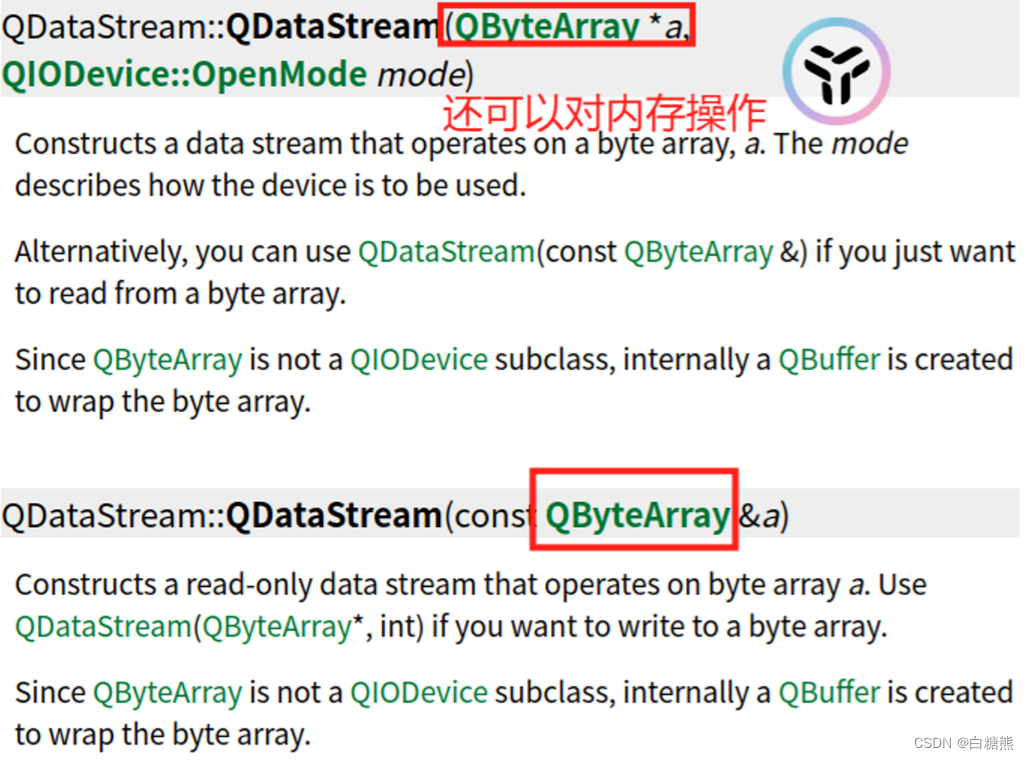
【QT】文件流操作(QTextStream/QDataStream)
文本流/数据流(二级制格式) 文本流 (依赖平台,不同平台可能乱码)涉及文件编码 #include <QTextStream>操作的都是基础数据类型:int float string //Image Qpoint QRect就不可以操作 需要下面的 …...

CentOS 7 devtoolset编译addressSanitizer版本失败的问题解决
在我的一个Cent OS7开发环境中,按https://yeyongjin.blog.csdn.net/article/details/134178420的方法升级GCC版本到8.3.1。 这两天,要用Google的addressSanitizer检验内存问题,加上编译参数后,却发现编译不通过。configure时直接退…...
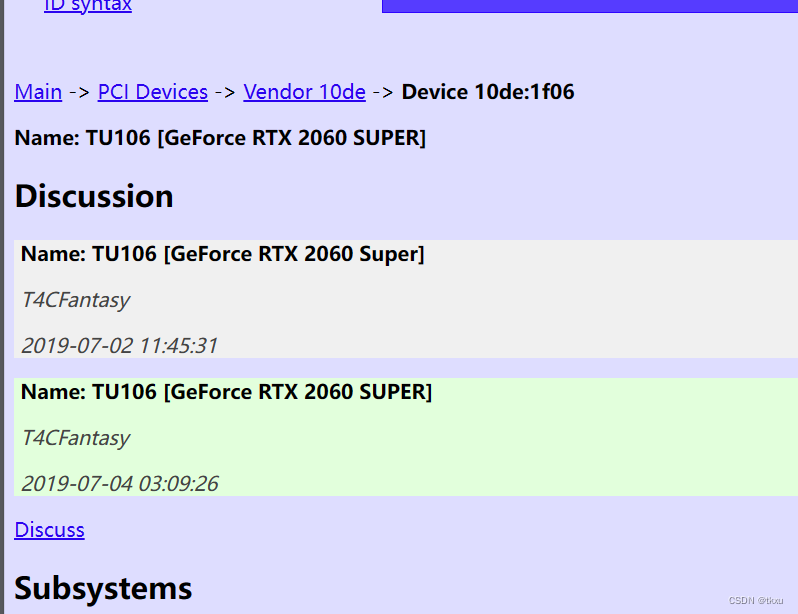
ubuntu2004桌面系统英伟达显卡驱动安装方法
#如何查看显卡型号 lspci | grep -i vga#----output------ 01:00.0 VGA compatible controller: NVIDIA Corporation Device 1f06 (rev a1)根据 Device 后的 值 进入网站查询 pci-ids.ucw.cz/mods/PC/10de?actionhelp?helppci #根据显卡型号,下载对应系统的驱动…...

Java通过Excel批量上传数据!!!
一、首先在前端写一个上传功能。 <template><!-- 文件上传 --><el-upload class"upload-demo" drag action"" :on-change"onChange" :auto-upload"false"><el-icon class"el-icon--upload"><up…...
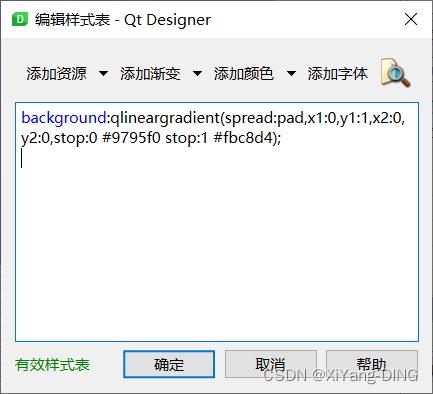
【PyQT/Pysider】控件背景渐变
默认渐变配色说明 background-color: qlineargradient(spread:pad, x1:0, y1:0, x2:1, y2:0, stop:0 rgba(255, 178, 102, 255), stop:0.55 rgba(235, 148, 61, 255), stop:0.98 rgba(0, 0, 0, 255), stop:1 rgba(0, 0, 0, 0));这段样式表使用了qlineargradient函数来创建…...

ChatGPT-4 VS 文心一言4.0
在线体验 地址(含 gpt 3.5 / 4.0,文心 3.5 / 4.0):https://chat.tool4j.com 点击访问 文心一言和ChatGPT-4都是非常强大的自然语言处理模型,它们都能够在对话系统和其他NLP应用中发挥巨大的作用。然而,它们…...

MYSQL------从概述到DQL
数据库(数据管理,数据存储的仓库) 数据库管理系统(操纵和管理数据库的大型软件) SQL是操作关系型的编程语言,是一套标准 MySQL下载安装完成以后,可以进行启动和停止操作,对于启动和停…...
(二))
MATLAB算法实战应用案例精讲-【图像处理】图像识别(基础篇)(二)
目录 数字图像处理基本知识 传统图像处理方法进行瑕疵检测 传统算法方向的选择...
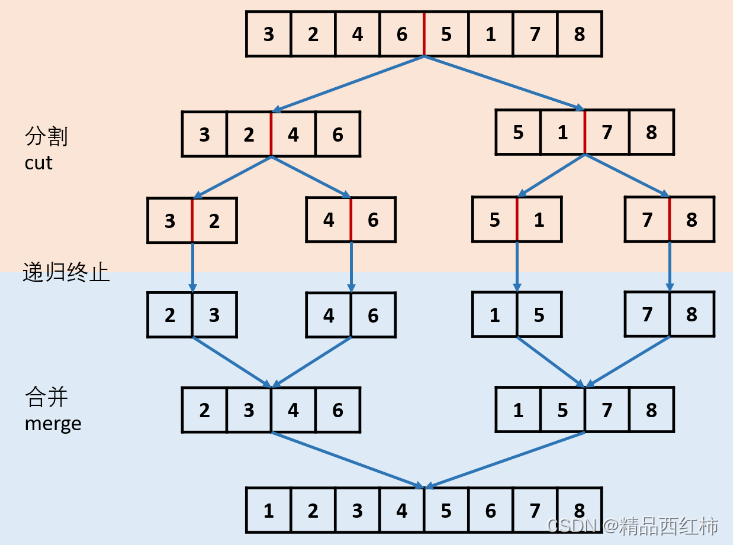
Leetcode 3.12
leetcode hot 100 链表1.两两交换链表中的节点2.随机链表的复制3.排序链表 链表 1.两两交换链表中的节点 两两交换链表中的节点 1.必须要设置一个dummy (temp) 结点2.保存第二个节点3.先让第一个节点指向第三个节点4.再让第二个节点指向第一个节点5.最后让dummy指向第二个节点…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
