git命令行提交——github
1. 克隆仓库至本地
git clone + 右键paste(github仓库地址)
cd + 仓库路径(进入到仓库内部准备提交文件等操作)
2. 查看main分支
git branch(列出本地仓库中的所有分支)
3. 创建新分支(可省略)
git branch dev1(dev1即为新分支)
git switch dev1(切换到名为 dev1 的分支)
然后需要在本地创建dev1文件夹,在该文件夹内就可以写入测试文件
4. 往分支dev1提交测试文件
git statusgit add .(add 和.之间有个空格)git commit -m "描述"git push origin dev1
然后就可以在github上查看了
5. 切换到main分支
git swatch main
在master分支(本地)添加文件并提交,和dev1分支一样的操作(也就是创建文件夹以后的操作)
6. 如果修改了文件,再次提交的操作
git status(使用 git status 命令查看修改的文件:这将显示出哪些文件已经被修改但还没有添加到暂存区。)git add .(将修改的文件添加到暂存区: 如果希望将所有修改过的文件添加到暂存区,如果只想添加特定的文件,可以将 . 替换为文件名或路径。)git commit -m "描述更改"( 提交更改到本地仓库: 添加到暂存区后,需要提交这些更改到本地仓库。在 -m 参数后面,可以添加一条描述性的提交信息。)git push origin main(将更改推送到远程仓库,这会将更改推送到名为 origin 的远程仓库的 main 分支上。如果使用的是其他分支,请将 main 替换为目标分支名称。)
7. 常用命令简记
- git init:在当前目录下初始化一个新的 Git 仓库。
- git clone <repository>:克隆远程仓库到本地。
- git status:显示工作目录的状态,包括已修改、已暂存和未跟踪的文件。
- git add <file>:将指定文件添加到暂存区。
- git commit -m "<message>":将暂存区的文件提交到本地仓库,<message> 是本次提交的描述信息。
- git push <remote> <branch>:将本地仓库的更改推送到远程仓库。
- git pull <remote> <branch>:从远程仓库拉取更改并合并到当前分支。
- git fetch <remote>:从远程仓库拉取最新的提交,但不合并到当前分支。
- git merge <branch>:将指定分支的更改合并到当前分支。
- git checkout <branch>:切换到指定分支。
- git branch:列出本地仓库的分支,创建、删除和重命名分支。
- git log:显示提交历史记录。
- git diff:显示工作目录和暂存区之间的差异。
- git remote -v:显示远程仓库的 URL。
- git remote add <name> <url>:添加一个新的远程仓库。
- git remote remove <name>:移除一个远程仓库。
- git reset <file>:从暂存区中移除指定文件,但保留工作目录中的修改。
- git reset --hard HEAD:将工作目录和暂存区重置为最新的提交。
- git stash:将当前的工作目录和暂存区保存为一个临时的堆栈状态,以便稍后恢复。
- git tag <tagname>:在当前提交上创建一个标签。
初学者可看,后续用到新的会继续详细更新其他的命令
相关文章:

git命令行提交——github
1. 克隆仓库至本地 git clone 右键paste(github仓库地址) cd 仓库路径(进入到仓库内部准备提交文件等操作) 2. 查看main分支 git branch(列出本地仓库中的所有分支) 3. 创建新分支(可省…...
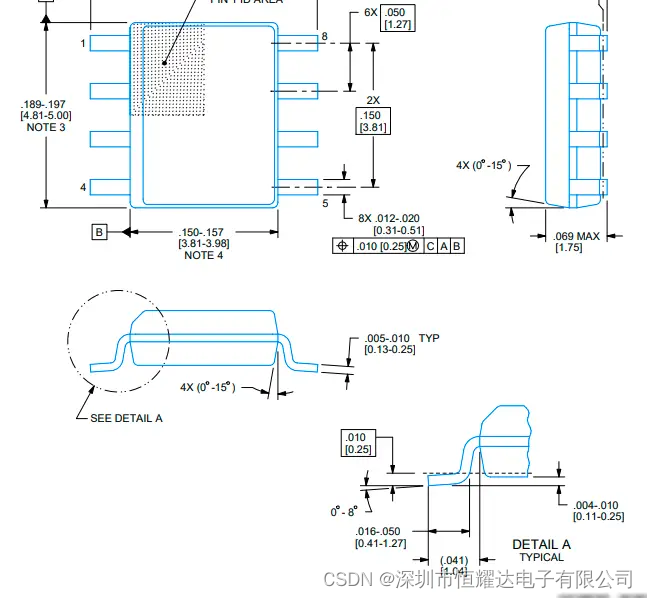
LM2903BIDR比较器芯片中文资料规格书PDF数据手册参数引脚图功能封装尺寸图
产品概述: M393B 和 LM2903B 器件是业界通用 LM393 和 LM2903 比较器系列的下一代版本。下一代 B 版本比较器具有更低的失调电压、更高的电源电压能力、更低的电源电流、更低的输入偏置电流和更低的传播延迟,并通过专用 ESD 钳位提高了 2kV ESD 性能和输…...

遍历list过程中调用remove方法
1、普通for循环遍历List删除指定元素,list.remove(index) List<String> nameList new ArrayList<>(Arrays.asList("张三", "李四", "王五", "赵六")); nameList.add("张七"); nameList.add("…...

Java解决罗马数字转整数
Java解决罗马数字转整数 01 题目 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 …...

无忧·企业文档v2.1.9新版本发布,全新升级,新变化让文档管理更无忧!
项目介绍 JVS是企业级数字化服务构建的基础脚手架,主要解决企业信息化项目交付难、实施效率低、开发成本高的问题,采用微服务配置化的方式,提供了 低代码数据分析物联网的核心能力产品,并构建了协同办公、企业常用的管理工具等&…...

【C语言_指针[2]_复习篇】
目录 一、数组名的理解 二、使用指针访问一维数组中的每个元素 三、一维数组传参的本质 四、冒泡排序 五、二级指针 六、指针数组 七、指针数组模拟二维数组 一、数组名的理解 1. 一般情况下,数组名就是数组首元素的地址。 2. 特殊情况1:sizeof(数…...

Rust 泛型使用过程中的 <T> 和 ::<T> 的区别
Rust 的泛型语法中,<T> 和 ::<T> 有不同的用途和上下文,但它们都与泛型有关。 <T> 在类型定义中 当你在定义函数、结构体、枚举或其他类型时,使用 <T> 来表示泛型参数。例如: fn identity<T>(x:…...

C语言 ——注释
1.1 单行注释 - 语法:// 待注释的内容 - 位置:可放在代码后,称之为行尾注释; 也可放代码上一行,称作行上注释。 c // 这是单行注释文字 1.2 多行注释 - 语法:/* 待注释的内容 */ - 注意:多⾏…...

C# 协程的使用
C# 中的协程是通过使用 yield 关键字来实现的,它们允许在方法的执行中暂停和继续。协程通常用于处理异步操作、迭代和状态机等情况。以下是关于C#协程的介绍、使用场景以及优缺点的概述: 介绍: 在 C# 中,协程是通过使用 yield 语…...

程序分享--C语言字母转换大小写的3种方法
关注我,持续分享逻辑思维&管理思维; 可提供大厂面试辅导、及定制化求职/在职/管理/架构辅导; 有意找工作的同学,请参考博主的原创:《面试官心得--面试前应该如何准备》,《面试官心得--面试时如何进行自…...
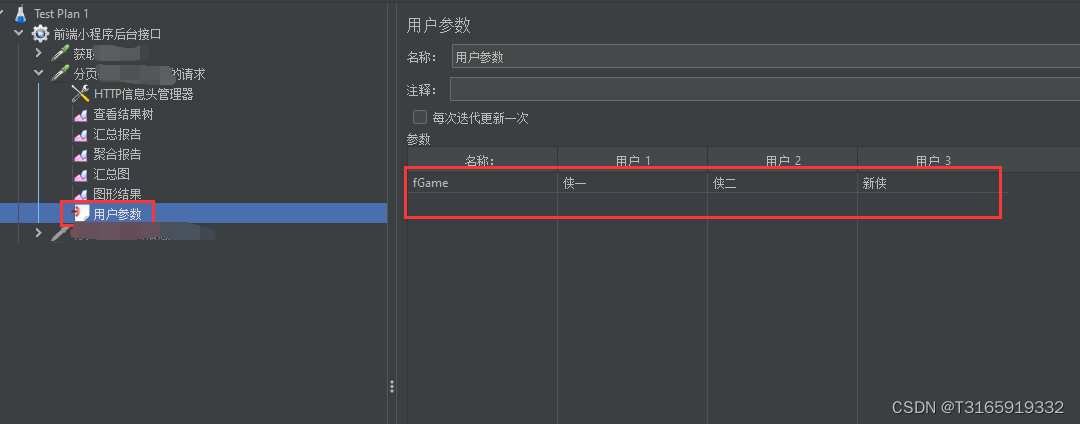
jmeter发送请求参数如何使用变量
问题描述 发送jmeter请求时,想设置请求参数为变量 解决方法...
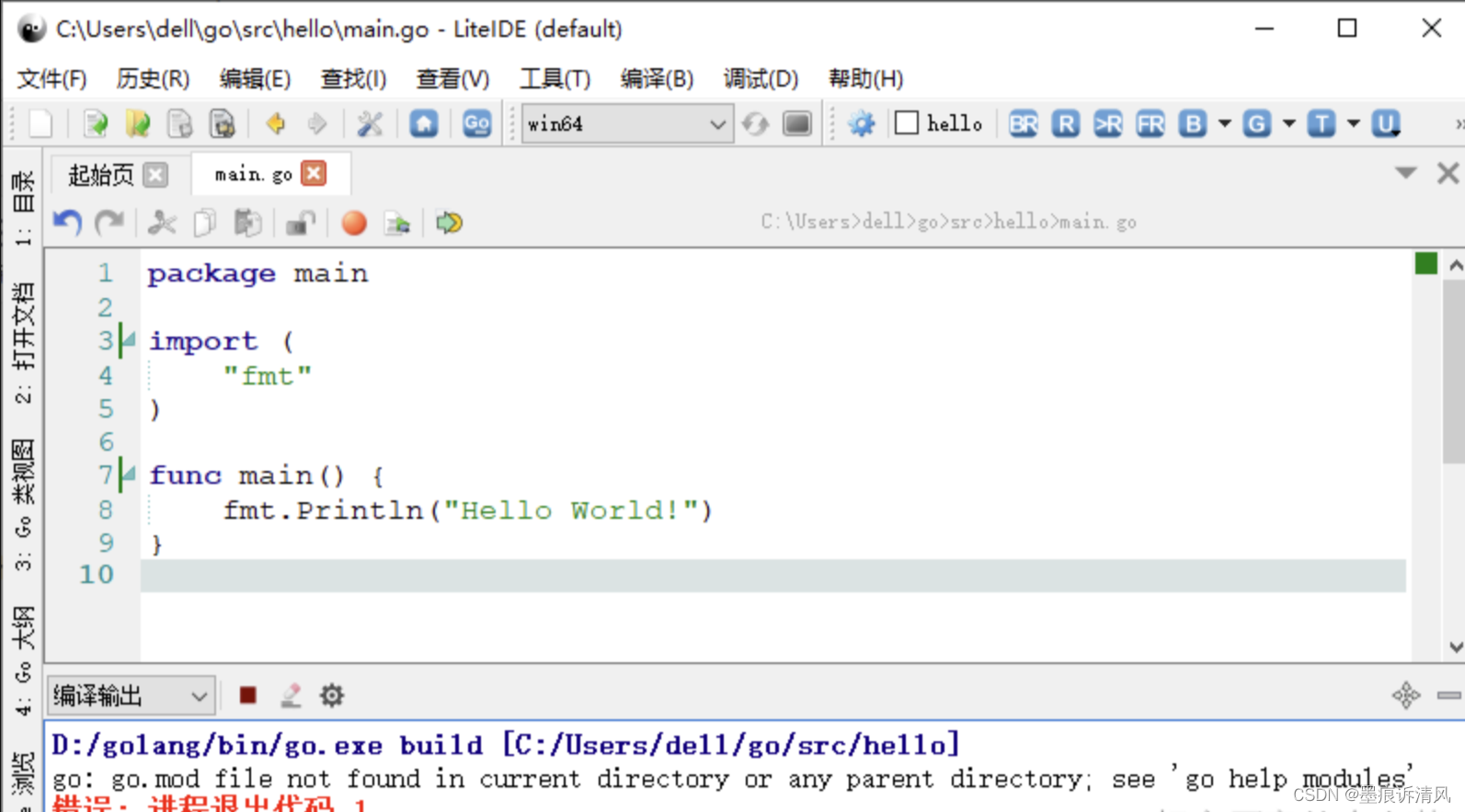
go go.mod file not found in current directory or any parent directory
场景: 安装好 liteide 之后创建了第一个 “hello world” 的golang 项目,却报了如下错误。 原因分析: go 的环境配置问题。与 golang 的包管理有关。 解决方案: 如果你是 Windows 系统,快捷键 “WinR”,…...

K8s的kubeadm方式部署集群实例
目录 一、准备环境 主机清单 修改主机名 设置防火墙、selinux状态 主机名解析 固定ip 重启网卡 同步时间 关闭swap分区 二、获取镜像 三、安装docker 四、配置kubeadm源 安装依赖包及常用插件 1.配置kubeadm源,安装对应版本 2.加载相关ipvs模块 3.配…...

GRU-深度学习循环神经网络情感分类模型搭建
摘要: 本文详细介绍了基于GRU的深度学习循环神经网络在情感分类任务中的应用,涵盖基础知识回顾、功能实现、技巧与实践、性能优化与测试,以及常见问题解答等环节。 阅读时长:约30分钟 关键词:GRU, 深度学习, 循环神经…...
- harbor镜像仓库)
ELK日志中心搭建(六)- harbor镜像仓库
CentOS 搭建 Harbor 镜像仓库(图文详解)_centos harbor-CSDN博客...

初识进程状态
🌎进程状态【上】 文章目录: 进程状态 发现进程的状态 运行队列 进程排队 进程状态的表述 状态在代码中的表示 运行状态 阻塞状态 挂起状态 总结 前言: 为了搞明白正在运行的进程是什么意思…...

线程的使用
目录 1,创建线程的几种方式 2,示例 3,线程常用方法 3.1 std::thread类 3.1.1 成员变量 3.1.2 thread成员函数 3.1.2.1 thread 构造函数 3.1.2.2 thread 析构函数 3.1.2.3 get_id 获取线程id 3.1.2.4 joinable 3.1.2.5 join 加入 …...
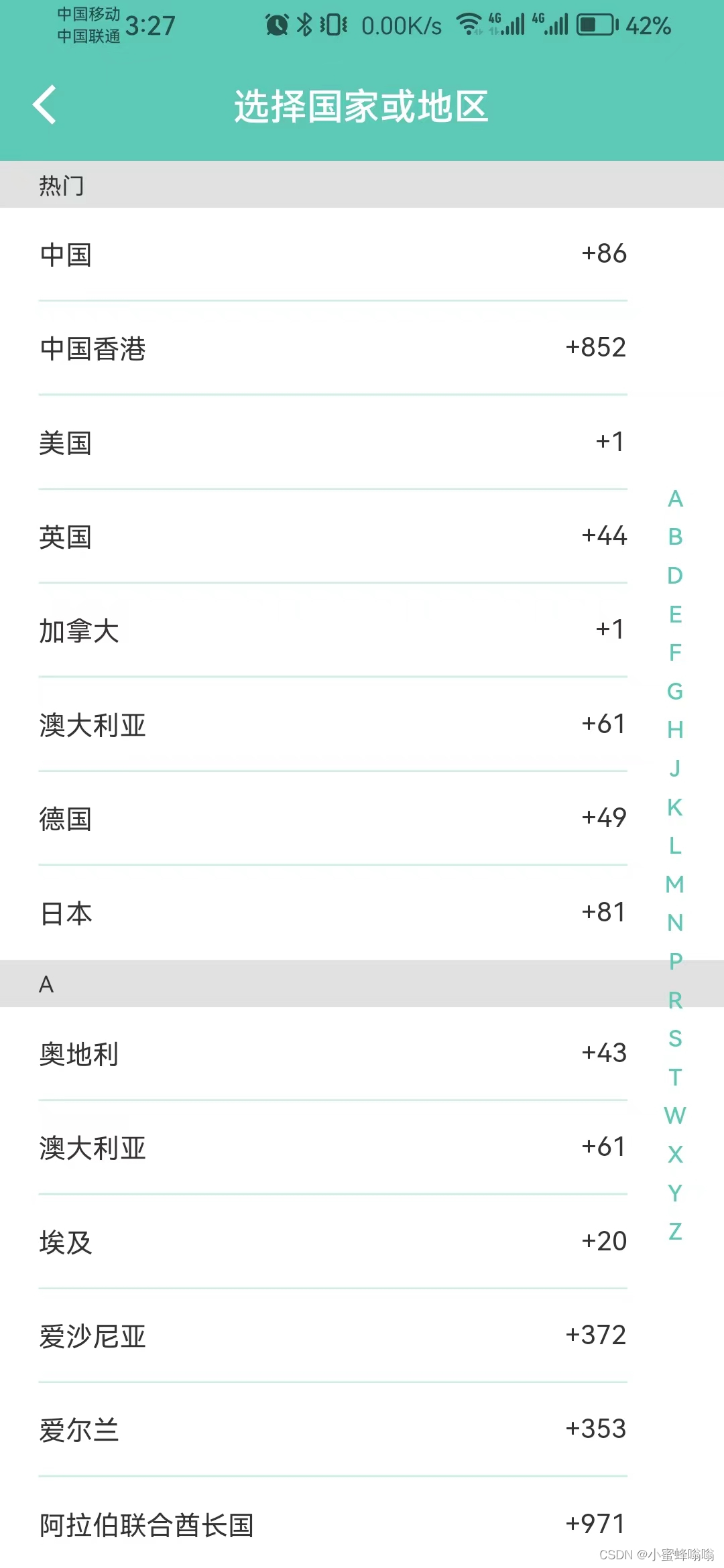
flutter选择国家或地区的电话号码区号
1.国家区号列表(带字母索引侧边栏) import package:generated/l10n.dart; import package:widget/login/area_index_bar_widget.dart; import package:flutter/material.dart; import package:flutter_screenutil/flutter_screenutil.dart;class LoginA…...
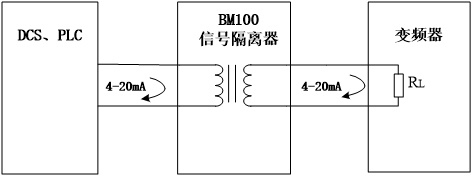
信号隔离器在PLC/DCS控制系统的应用
彭姝麟 Acrelpsl 概述: 随着工业自动化程度的不断提高,变频器也得到了非常广泛的应用。作为电力电子器件,变频器中要进行大功率二极管整流,大功率晶体管变压,在输入输出回路产生电流高次谐波,干扰供电系统、负载以及附…...
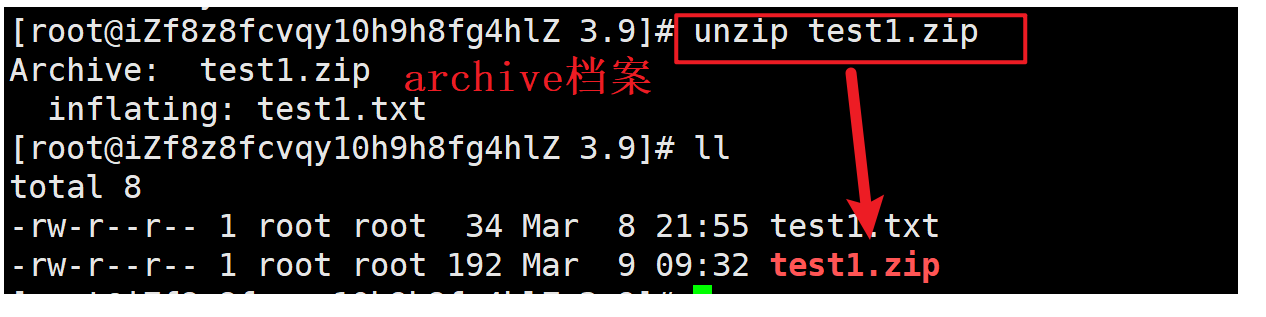
探索Linux世界:基本指令(文件查看、时间相关、grep、打包压缩及相关知识)
今天继续介绍一些指令 文章目录 1.cat - 查看文件1.1输出重定向和追加重定向1.2指令echo 2.more 指令3.less - 逐页查看文本文件内容4.head- 显示文件开头部分内容5.tail - 显示文件末尾部分内容5.1输入重定向(<)5.2管道(|) 6.…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
