基于机器学习的曲面拟合方法
随着科技的不断发展,机器学习成为了最近最热门的技术之一,也被广泛应用于各个领域。其中,基于机器学习的曲面拟合方法也备受研究者们的关注。曲面拟合是三维模型处理中的重要技术,其目的是用一组数据点拟合出平滑的曲面,为后续的几何建模和分析铺平道路。
重点介绍三种基于机器学习的曲面拟合方法: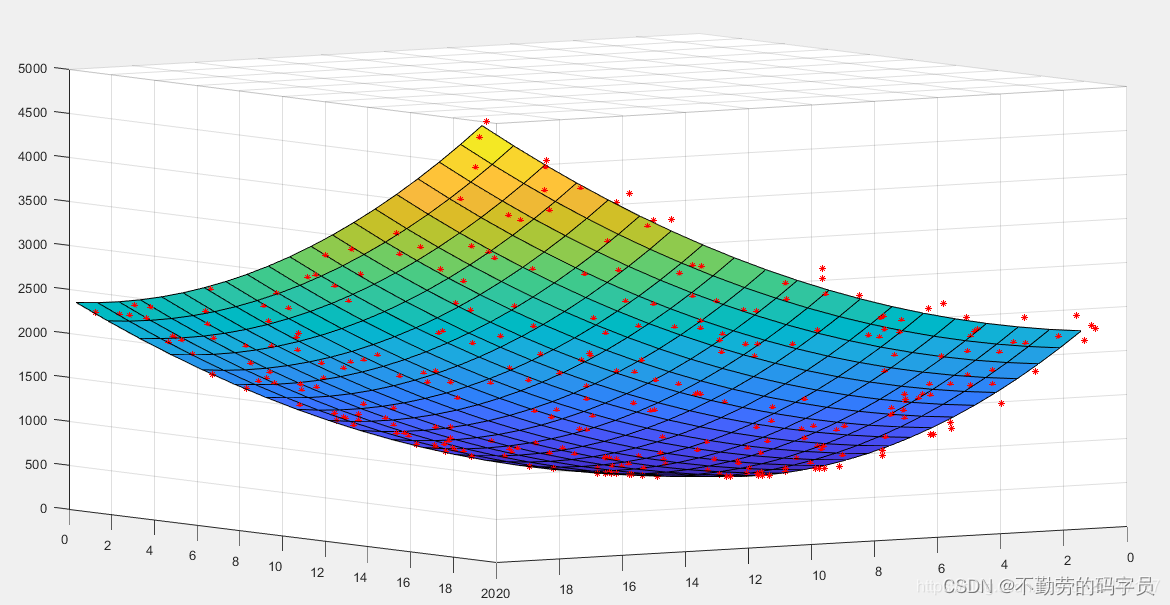
- 基于支持向量机的曲面拟合;
- 基于独经网络的曲面拟合;
- 基于决策树的曲面拟合。
一、基于支持向量机的曲面拟合
支持向量机是一种分类器,常用于分类和回归分析中。其基本思想是通过寻找最优超平面将数据分为两类,并最大化各类数据点到超平面的间隔。在曲面拟合中,支持向量机可以用来处理非线性问题,即使数据集中带有噪音或孤立点,也可以获得很好的效果。其优势在于可以通过调节参数来控制预测函数的复杂度,从而在保持精度的同时避免过拟合。
二、基于神经网络的曲面拟合
神经网络是一种模拟大脑思维过程的学习算法,常用于处理非线性问题。在曲面拟合中,神经网络可以识别和学习实际数据集中的模式,从而拟合出可靠的曲面。其优势在于可以自适应地调整权值和阈值,从而实现精确的拟合。但需要注意的是,神经网络需要大量的训练数据来避免过拟合,并且需要对网络结构进行仔细的设计和调整。
三、基于决策树的曲面拟合
决策树是一种基于树形结构的分类和回归模型,其基本思想是将数据集分解成小的、易于管理的子集。在曲面拟合中,决策树可用于非线性问题,可以从数据集中获得清晰的模式,从而能够准确地拟合出曲面。其优势在于可以通过简单的决策规则来识别模式并学习数据,训练时间短,可解释性强。
相关文章:

基于机器学习的曲面拟合方法
随着科技的不断发展,机器学习成为了最近最热门的技术之一,也被广泛应用于各个领域。其中,基于机器学习的曲面拟合方法也备受研究者们的关注。曲面拟合是三维模型处理中的重要技术,其目的是用一组数据点拟合出平滑的曲面࿰…...

【C++从练气到飞升】03---构造函数和析构函数
🎈个人主页:库库的里昂 ✨收录专栏:C从练气到飞升 🎉鸟欲高飞先振翅,人求上进先读书。 目录 ⛳️推荐 一、类的6个默认成员函数 二、构造函数 1. 构造函数的概念 2. 构造函数的定义 3. 构造函数的特性 三、析构函…...

mybatis转义字符
编写SQL中会用到<,>,<,> 等,但是在mybatis中不可以这么写,与xml文件的元素<>冲突,所以需要转义。整理转义字符如下: 符号原始字符转义字符大于>>大于等于>>小于<<小于等于<<和&&a…...
vue3 实现一个tab切换组件
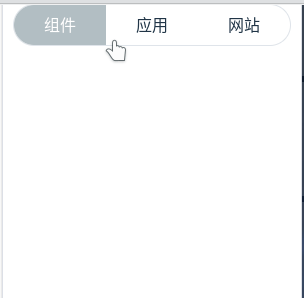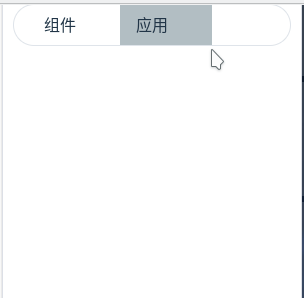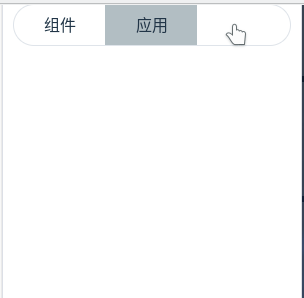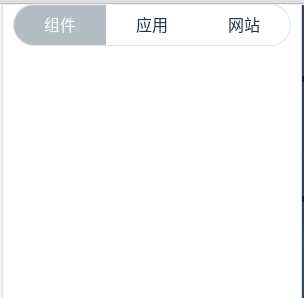
一. 效果图 二. 代码 文件 WqTab.vue: <template><div ref"wqTabs" class"wq-tab"><template v-for"tab in tabs" :key"tab"><div class"tab-item" :class"{ ac: tabActive tab.key }" c…...

JSONObject在Android Main方法中无法实例化问题
目录 前言一、Main(非安卓环境)方法下运行二、安卓坏境下运行三、why? 前言 原生的json,即org.json.JSONObject; 在Android Studio中的Main方法里运行报错,但在安卓程序运行过程正常 一、Main(非安卓环境)方法下运行 static void test() {try {// 创建一个 JSON …...

京津冀协同发展:北京·光子1号金融算力中心——智能科技新高地
京津冀协同发展是党中央在新的历史条件下提出的一项重大国家战略,对于全面推进“五位一体”总体布局,以中国式现代化全面推进强国建设、民族复兴伟业,具有重大现实意义和深远历史意义。随着京津冀协同发展战略的深入推进,区域一体…...

aspnetcore使用jwt时一直提示401 authorization
测试aspnetcore使用Jwt做认证授权的时候,一直提示401 Authorization 最后发现问题所在,希望能有所帮助 1.检查注册了认证和授权中间件 缺一不可 /*认证*/app.UseAuthentication();/*授权*/app.UseAuthorization();2.检查swagger的配置项 builder.Servic…...
三款文案自动生成器,帮你轻松生成原创文案
文案在今天已经成为了许多企业和个人推广产品和服务的重要手段。然而,对于很多人来说,写作文案并非易事。有时候,我们可能会遇到文案灵感枯竭的情况,或者花费大量时间在寻找合适的词句上。但是,别担心!现在…...

多线程并发模拟实现与分析:基于Scapy的TCP SYN洪水攻击实验研究
简介 实现基于Python实现的多线程TCP SYN洪水攻击。该实例利用Scapy库构造并发送TCP SYN数据包,通过多线程技术模拟并发的网络攻击行为。 实现原理 SYN Flood攻击是一种经典的分布式拒绝服务(DDoS)攻击方式,利用了TCP协议握手过…...
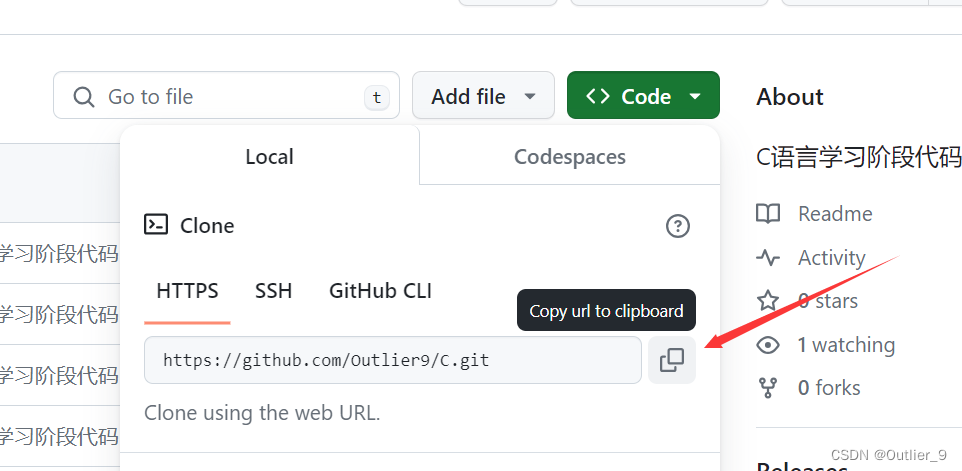
git命令行提交——github
1. 克隆仓库至本地 git clone 右键paste(github仓库地址) cd 仓库路径(进入到仓库内部准备提交文件等操作) 2. 查看main分支 git branch(列出本地仓库中的所有分支) 3. 创建新分支(可省…...
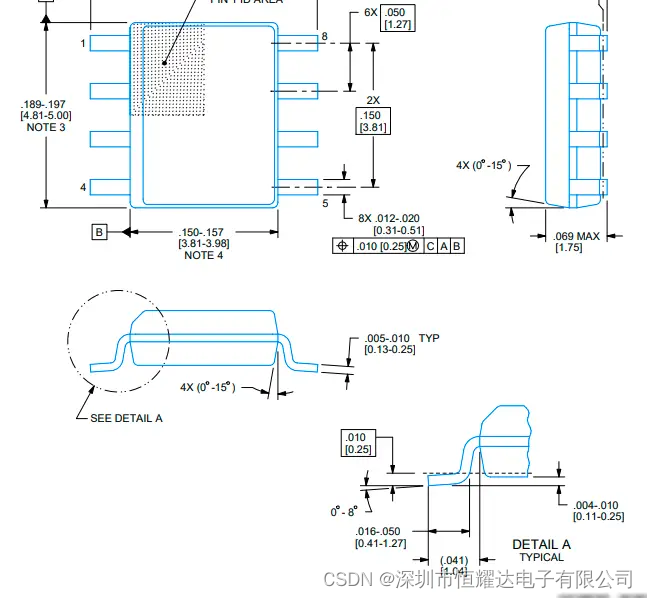
LM2903BIDR比较器芯片中文资料规格书PDF数据手册参数引脚图功能封装尺寸图
产品概述: M393B 和 LM2903B 器件是业界通用 LM393 和 LM2903 比较器系列的下一代版本。下一代 B 版本比较器具有更低的失调电压、更高的电源电压能力、更低的电源电流、更低的输入偏置电流和更低的传播延迟,并通过专用 ESD 钳位提高了 2kV ESD 性能和输…...

遍历list过程中调用remove方法
1、普通for循环遍历List删除指定元素,list.remove(index) List<String> nameList new ArrayList<>(Arrays.asList("张三", "李四", "王五", "赵六")); nameList.add("张七"); nameList.add("…...

Java解决罗马数字转整数
Java解决罗马数字转整数 01 题目 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 …...

无忧·企业文档v2.1.9新版本发布,全新升级,新变化让文档管理更无忧!
项目介绍 JVS是企业级数字化服务构建的基础脚手架,主要解决企业信息化项目交付难、实施效率低、开发成本高的问题,采用微服务配置化的方式,提供了 低代码数据分析物联网的核心能力产品,并构建了协同办公、企业常用的管理工具等&…...

【C语言_指针[2]_复习篇】
目录 一、数组名的理解 二、使用指针访问一维数组中的每个元素 三、一维数组传参的本质 四、冒泡排序 五、二级指针 六、指针数组 七、指针数组模拟二维数组 一、数组名的理解 1. 一般情况下,数组名就是数组首元素的地址。 2. 特殊情况1:sizeof(数…...

Rust 泛型使用过程中的 <T> 和 ::<T> 的区别
Rust 的泛型语法中,<T> 和 ::<T> 有不同的用途和上下文,但它们都与泛型有关。 <T> 在类型定义中 当你在定义函数、结构体、枚举或其他类型时,使用 <T> 来表示泛型参数。例如: fn identity<T>(x:…...

C语言 ——注释
1.1 单行注释 - 语法:// 待注释的内容 - 位置:可放在代码后,称之为行尾注释; 也可放代码上一行,称作行上注释。 c // 这是单行注释文字 1.2 多行注释 - 语法:/* 待注释的内容 */ - 注意:多⾏…...

C# 协程的使用
C# 中的协程是通过使用 yield 关键字来实现的,它们允许在方法的执行中暂停和继续。协程通常用于处理异步操作、迭代和状态机等情况。以下是关于C#协程的介绍、使用场景以及优缺点的概述: 介绍: 在 C# 中,协程是通过使用 yield 语…...

程序分享--C语言字母转换大小写的3种方法
关注我,持续分享逻辑思维&管理思维; 可提供大厂面试辅导、及定制化求职/在职/管理/架构辅导; 有意找工作的同学,请参考博主的原创:《面试官心得--面试前应该如何准备》,《面试官心得--面试时如何进行自…...
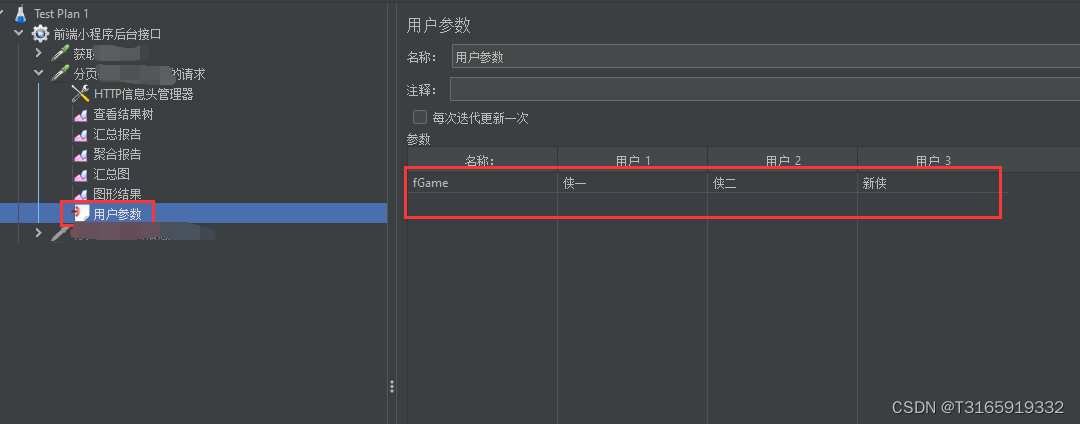
jmeter发送请求参数如何使用变量
问题描述 发送jmeter请求时,想设置请求参数为变量 解决方法...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
