【LeetCode 算法专题突破】---二分查找(⭐⭐⭐)
前言
我在算法题目的海洋中畅游已久,也曾在算法竞赛中荣获佳绩。然而,我发现自己对于算法的学习,还缺乏一个系统性的总结和归类。尽管我已经涉猎过不少算法类型,但心中仍旧觉得有所欠缺,未能形成完整的算法体系。
因此,我决定踏上这次算法之旅,对常见的算法进行一次全面的梳理与归类。我希望通过这个过程,能够更深入地理解每个经典算法类型的核心知识,加强我的算法能力,并完善自己的算法体系。
同时,我也希望能够将这次学习的成果与你分享,希望对你也有所帮助。让我们一同在算法的世界里探索、成长,共同迎接未来的挑战吧!
1.经典的不能在经典的二分查找(难度⭐)
Leetcode链接:704. 二分查找
1.1题目描述:

这是一道非常典型的二分查找算法题目,可以说所有要学习二分查找算法的人都必须掌握这道题。题目要求很简单,就是在一个有序数组中查找目标值target。这道题是二分查找算法的入门题和模版题,没有掌握这道题就无法开始学习更复杂的二分查找算法题目。所以这道题对于二分查找算法的理解和掌握非常关键和必要。
1.2代码:
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;int mid;while(left <= right){mid = (left + right)/2;if(nums[mid]>target){right = mid - 1;}else if(nums[mid]<target){left = mid + 1;}else{return mid;}}return -1;}
};通过这道二分查找的典型题,我对二分查找算法的理解更进一步:
我对二分查找的区间划分有了更深的理解:
- 当mid位置的值小于target时,证明左区间[left, mid-1]都不可能存在target,所以左区间变为[mid+1, right]。
- 当mid位置的值大于target时,证明右区间[mid+1, right]都不可能存在target,所以右区间变为[left, mid-1]。
- 当mid位置的值等于target时,就找到了目标值。
我理解到二分查找的本质就是通过比较中间mid值与target的值,可以排除一半的搜索区间,使搜索范围越来越小,直到找到target。
通过这道题我对二分查找算法模板有了更加熟练的掌握,可以应用到其他二分查找题目中去。
2.在排序数组中查找元素的第一个和最后一个位置(难度⭐⭐)
Leetcode链接:34. 在排序数组中查找元素的第一个和最后一个位置
2.1题目描述:

2.2代码:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1, begin = -1, end = -1, mid;//找到区间左边界while(left<=right){mid = (left + right)/2;if(nums[mid] > target){right = mid - 1;}else if(nums[mid] < target){left = mid + 1;}else{begin = mid;right--;//right区间左移,使得mid左移,直到到达左区间边界,此时right正好和left重合}}left = 0, right = nums.size() - 1;//找到区间有边界while(left<=right){mid = (left + right)/2;if(nums[mid] > target){right = mid - 1;}else if(nums[mid] < target){left = mid + 1;}else{end = mid;left++;//left区间右移,使得mid右移,直到到达又区间边界,此时left正好和right重合}}return {begin,end};}
};这道题的大思路和上面的题并没有太大区别,只是为了找到左右区间,需要两次二分查找
具体来说,在求左右区间边界时,处理mid==target的情况需要进行特别考虑:
- 求左区间边界时,需要在记录begin索引后,继续将right索引左移,使得mid向左逼近,直到不等于target时才能锁定左区间边界。
- 求右区间边界时,需要在记录end索引后,继续将left索引右移,使得mid向右逼近,直到不等于target时才能锁定右区间边界。
这种细微的逻辑调整体现了二分查找的灵活性,在保持模板框架不变的情况下,通过简单逻辑修改就可应对新的问题。
3. 有效的完全平方数(难度⭐)
Leetcode链接:367. 有效的完全平方数
3.1题目描述:

撇开具体问题不讨论,假设需要找到完全平方数,你可能会采用这样的方法:将原数进行二分,然后将得到的中间值平方,观察是否等于目标值。如果相等,那么找到了完全平方数;如果不等,就可以根据大小关系缩小搜索范围,继续二分。为什么选择这种方式呢?因为这种方法的效率相对较高。既然如此,我们为何不考虑运用二分法来解决这类问题呢?
3.2代码:
class Solution {
public:bool isPerfectSquare(int num) {long long left = 0, right = num, mid = 0;long long s;while(left<=right){mid = (left + right)/2;s = mid * mid;if(s>num){right=mid-1;}else if(s<num){left=mid+1;}else{return true;}}return false;}
};在这个解决方案中,我们并没有深入探讨具体的代码细节,只是简单地将二分算法应用于这个场景。然而,通过这个简单的经验,我们可以得出一个更加广泛的启示:如果今后遇到类似的问题,我们可以考虑运用二分法。
4.寻找峰值(难度⭐⭐)
二分熟练度up up up~
Leetcode链接:162. 寻找峰值
4.1题目描述:

在面对这个问题时,我们甚至没有提供目标值(target),而且输入序列并不保证是有序的。这是否意味着我们可以应用二分查找算法呢?
让我们尝试通过代码来展示这一思路,看看是否能够在这样的条件下成功运用二分查找的思想解决问题。
4.2代码:
class Solution {
public:int findPeakElement(vector<int>& nums) {int left = 0, right = nums.size() - 1, mid = 0;while(left<right){mid = (left + right)/2;if(nums[mid]>nums[mid + 1]){right = mid;}else{left = mid + 1;}}return right;}
};初看之下,面对问题好像难以着手,但让我们仔细分析一下,看看能否找到解决方案。
题目要求在数组中找到任意一个峰值,那么我们可以考虑将数组分为两个区间:一个是递增区间,另一个是递减区间。峰值实际上是这两个区间的交界点。
假设我们随机选择一个点进行比较,如果它比右侧位置的值小,说明它在一个递增的区间;反之,如果它比右侧位置的值大,说明它在一个递减的区间。
基于这个性质,我们可以运用二分算法。当 nums[mid] < nums[mid+1] 时,表示在一个递增区间,峰值必定在 mid+1 及其之后的位置;而当 nums[mid] > nums[mid+1] 时,表示在一个递减区间,峰值可能在 mid 或其之前的位置(需要注意,峰值有可能就是在 mid 位置)。
因此,我们更新 right = mid,而不需要进行 -1 的操作。由于不需要 -1,当 left == right 时,如果已经找到峰值,我们应该如何退出循环呢?
这里可以进行特殊处理,或者将循环条件改成 left < right。在某些情况下,模板并不是固定不变的,我们可以根据实际情况进行调整。通过解决这道题,我们不仅学到了一些技巧,也积累了宝贵的经验。
5.寻找旋转排序数组中的最小值(难度⭐⭐)
Leetcode链接:153. 寻找旋转排序数组中的最小值
5.1题目描述:

这题的解题思路与前面一道问题相似,我们需要根据所给的条件找到一个可以进行比较的参照物或者说参照系。让我们来审视一下具体的代码。
5.2代码:
class Solution {
public:int findMin(vector<int>& nums) {int n = nums.size() - 1;int left = 0, right = n, mid = 0;while(left < right){mid = (left + right)/2;if(nums[mid] > nums[n]){left = mid + 1;}else if(nums[mid] < nums[n]){right = mid;}}return nums[left];}
};考虑到题目给出的是一个经过旋转的升序数组,这使得数组不再是有序的,我们需要思考如何运用二分法来解决这一问题。
观察到,经过旋转的升序数组可以分为两个递增的区间,一个较大的区间和一个较小的区间。我们可以以区间的最大值作为参照物来进行分析。
以最右边的元素为例,它可能是小区间的最大值,也可能是大区间的最大值。如果它是大区间的最大值,这就意味着数组没有经过旋转,因此我们可以先忽略这种特殊情况(这是一个解题的小技巧,特殊情况可以后续再处理)。
题目要求找到最小的元素,即小区间的最小值。因此,我们需要找到小区间,并在其中找到最小元素。具体操作如下:
- 当 nums[mid] > nums[n] 时,表示中间位置 mid 处于大区间,因此将 left 调整为 mid + 1;
- 当 nums[mid] < nums[n] 时,表示中间位置 mid 处于小区间,因此将 right 调整为 mid。注意,这里不能减1,因为我们要找的值在小区间内,不能排除掉中间元素。
- 接着,考虑特殊情况,即当 nums[mid] < nums[n] 时,数组的最右元素 n 是大区间的最大值。如果我们让 right = mid,会导致最终循环结束时出现 left = right 的情况。为了避免这种情况,我们将循环的条件调整为 left < right。
这道题是二分法的一个变式,关键在于找到以何为参照系来确定区间的位置,一旦确定,后续的工作就变得相对容易。
6.点名(难度⭐)
Leetcode链接:LCR 173. 点名
6.1题目描述:

这道题我其实一开始也想不出来,选这道题的目的其实也是想说明,算法积累的重要性,见多识广,才能思路开阔,临危不乱。
6.2代码:
class Solution
{
public:int takeAttendance(vector<int>& records) {int n = records.size() - 1;int left = 0, right = n, mid = 0;while(left < right){mid = (left + right)/2;if(records[mid] == mid){left = mid + 1;}else{right = mid;}}if (records[right] == right) {return right+1;}return right;}
};总结一下:
完成了这六道题目后,相信你对二分查找已经得心应手了~
接下来,继续努力,迎接新的挑战吧~
如果有一天觉得对二分有些生疏了,不妨回来再刷一遍,巩固一下技能~
最后,祝愿你未来的刷题之路愉快顺利~
相关文章:

【LeetCode 算法专题突破】---二分查找(⭐⭐⭐)
前言 我在算法题目的海洋中畅游已久,也曾在算法竞赛中荣获佳绩。然而,我发现自己对于算法的学习,还缺乏一个系统性的总结和归类。尽管我已经涉猎过不少算法类型,但心中仍旧觉得有所欠缺,未能形成完整的算法体系。 因…...

一个简单的HTML 个人网页
<!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <title>个人网页</title> <style> body { f…...

【SpringCloud微服务实战05】Feign 远程调用
Feign是一个由Netflix开发的轻量级RESTful HTTP服务客户端,用于简化和优雅地调用HTTP API。它允许用户通过Java接口注解来发起请求,而不必像传统方式那样手动构建HTTP请求报文。Feign支持Spring Cloud解决方案,使得服务消费者能够像调用本地接口方法一样调用远程服务。使得开…...

LiveGBS流媒体服务器中海康摄像头GB28181公网语音对讲、语音喊话的配置
LiveGBS海康摄像头国标语音对讲大华摄像头国标语音对讲GB28181语音对讲需要的设备及服务准备 1、背景2、准备2.1、服务端必备条件(注意)2.2、准备语音对讲设备2.2.1、不支持跨网对讲示例2.2.2、 支持跨网对讲示例 3、开启音频开始对讲4、搭建GB28181视频…...

【前端】尚硅谷Webpack教程笔记
文章目录 1. 基本使用1.1 功能介绍1.2 开始使用 参考视频:尚硅谷Webpack5入门到原理 课件地址 【前端目录贴】 1. 基本使用 1.1 功能介绍 Webpack 是一个静态资源打包工具。 它会以一个或多个文件作为打包的入口,将我们整个项目所有文件编译组合成一个或多个文件输…...

Java泛型使用及局限
Java泛型的局限和使用经验 泛型的局限 任何基本类型不能作为类型参数 经过类型擦除后,List中包含的实际上还是Object的域,而在Java类型系统中Object和基本类型是两套体系,需要通过“自动装包、拆包机制”来进行交互。 2.任何在运行时需要…...

Sklearn线性回归
Scikit-learn 中的线性回归是一个用于监督学习的算法,它用于拟合数据集中的特征和目标变量之间的线性关系。以下是使用 Scikit-learn 实现线性回归的基本步骤: 1. 导入所需库 首先,你需要导入所需的库和模块。 import numpy as np import …...
APP中互联网公司的必备知识
APP中互联网公司的必备知识 敏捷开发(scrum)模型角色工作流程 项目上线发布策略发布流程灰度发布 APP发布APP软件包类型APP客户端(内部)发布平台APP客户端(线上)发布平台 熟悉APP项目(tpshop&am…...

论文翻译 - Visual Adversarial Examples Jailbreak Large Language Models
论文链接:https://arxiv.org/pdf/2306.13213.pdf 项目代码:https://github.com/Unispac/Visual-Adversarial-Examples-Jailbreak-Large-Language-Models Visual Adversarial Examples Jailbreak Aligned Large Language Models Abstract1 Introduction2 …...

android so载入过程
源自android 9 看源代码的网页 /bionic/libdl/libdl_static.c 好像没用。都是空的 /bionic/libdl/libdl.cpp 主角 22// These functions are exported by the loader 23// TODO(dimitry): replace these with reference to libc.so101// Proxy calls to bionic loader 102_…...
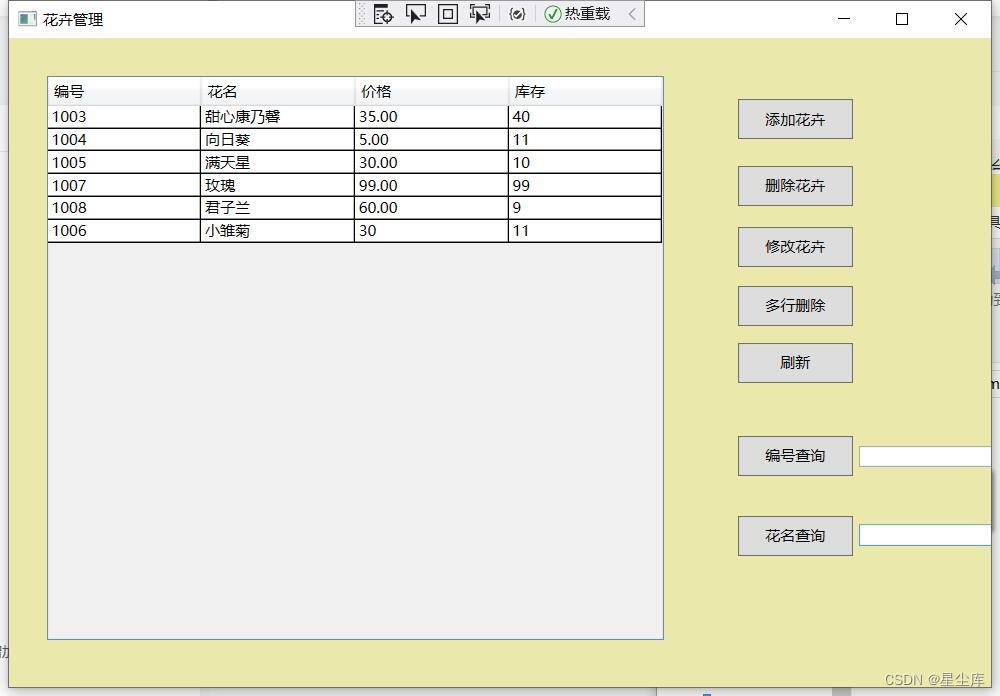
FlowerShop花店管理系统wpf+sqlserver
FlowerShop花店管理系统wpfsqlserver说明文档 运行前附加数据库.mdf(或sql生成数据库) 主要技术: 基于C#wpf架构和sql server数据库 功能模块: 顾客登录后可以查询花卉详情然后购买 店主登录管理后台 顾客管理 删除顾客多行删…...
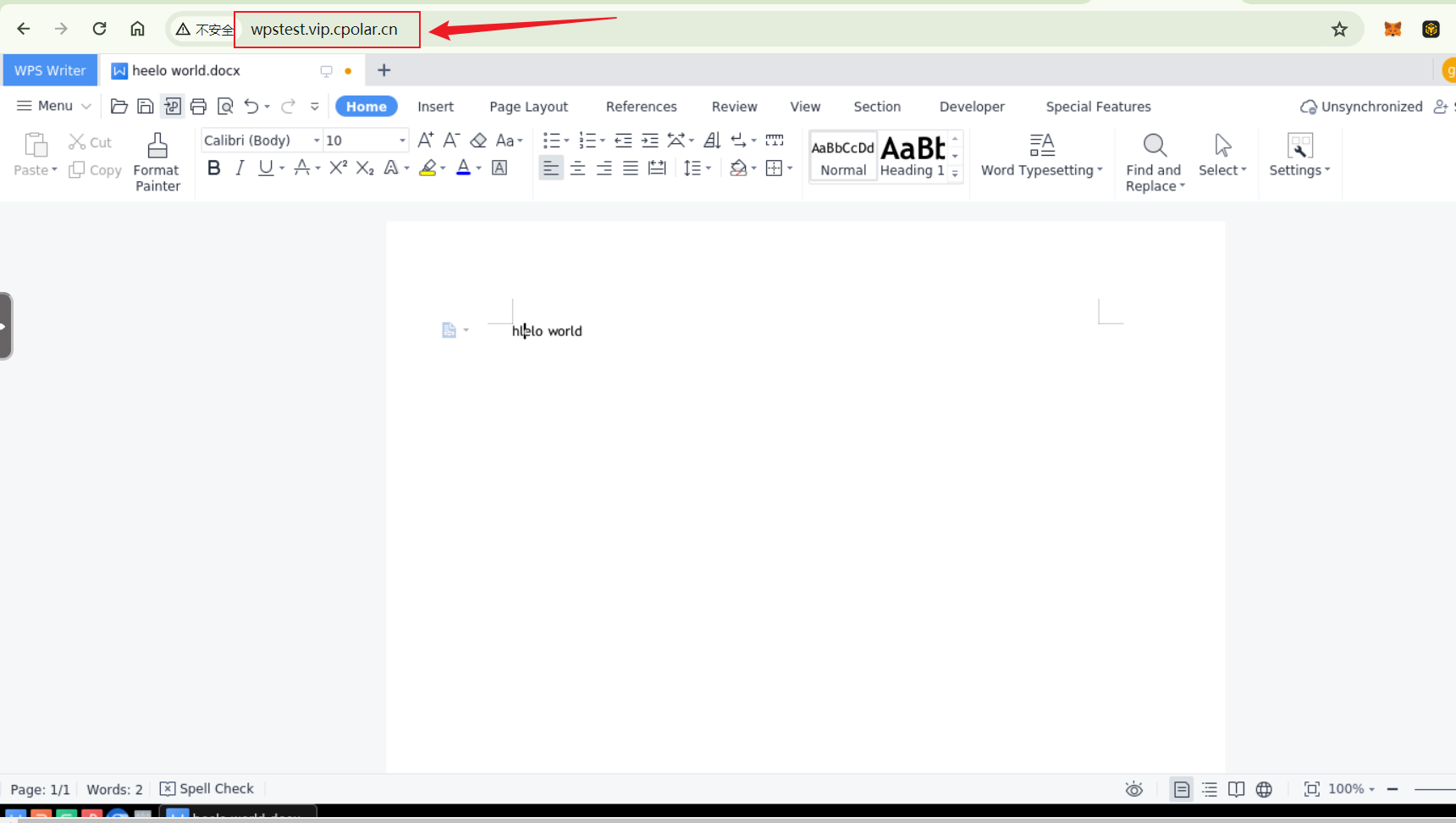
如何在群晖NAS部署WPS容器并实现无公网IP远程访问本地office软件
文章目录 1. 拉取WPS Office镜像2. 运行WPS Office镜像容器3. 本地访问WPS Office4. 群晖安装Cpolar5. 配置WPS Office远程地址6. 远程访问WPS Office小结 7. 固定公网地址 wps-office是一个在Linux服务器上部署WPS Office的镜像。它基于WPS Office的Linux版本,通过…...

【C语言程序设计】C语言求圆周率π(三种方法)
题目一: 利用公式①计求π的近似值,要求累加到最后一项小于10^(-6)为止。 程序代码: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(){float s1;float pi0;float i1.0;float n1.0;while(fabs(i)&…...

常见的特殊端口号及其用途
21端口:FTP(文件传输协议)服务端口。FTP允许用户进行文件传输,如上传和下载文件。22端口:SSH(安全外壳协议)服务端口。SSH用于远程登录到服务器,并提供加密的数据传输。23端口&#…...
 安装kotlin)
Linux(ubuntu) 安装kotlin
Kotlin 是一种基于 Java 语言的静态类型编程语言,它可以运行于 JVM 上 1. 安装 Java Development Kit (JDK) Kotlin 运行于 JVM 上,所以首先需要安装 Java Development Kit(JDK) Ubuntu 或 Debian 系统 sudo apt update sudo a…...

微信小程序提交成功设置提示
在微信小程序中,当用户成功提交表单或完成某项操作后,通常我们会设置一个提示来告知用户操作已完成。这种提示通常可以通过几种方式来实现,例如使用 wx.showToast 方法显示一个短暂的提示消息,或者跳转到一个新的页面并显示成功信…...
Pycharm与Anaconda安装
网址: Pycharm:https://www.jetbrains.com/pycharm/ Anaconda:https://www.anaconda.com/download/ 官网下载速度太慢可以选择到清华源下载:https://repo.anaconda.com/archive/ 一:Anaconda安装 安装: …...
阿里云数据盘挂载目录
1、先登录服务器创建新目录aaa 2、云盘都快照备份下。后续操作完核实无误了,您根据您需求删除快照就行, 然后登录服务器内执行: fdisk -l lsblk blkid ll /aaa 3、执行:(以下命令是进行数据盘做ext4文件系统并挂载到…...

【Python】探索PyPinyin 库:Python 中的中文拼音转换工具
花未全开月未圆, 半山微醉尽余欢。 何须多虑盈亏事, 终是小满胜万全。 —— 《对抗路—吕布》 PyPinyin 是一个功能强大的 Python 库,用于将中文文本转换为拼音。它提供了丰富的功能,能够满足各种中文文本处理的需求。在本文中&am…...

Linux运维总结:Centos7.6之OpenSSH7.4升级版本至9.3
一、环境信息 操作系统:Centos7.6.1810 OpenSSH_7.4p1, OpenSSL 1.0.2k-fips 注意:升级后由于加密算法的区别,低版本的SSH工具可能无法连接,建议改用Xshell7或SecureCRT9.0以上版本。 二、注意事项 1、 检查防火墙或selinux是否…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
