代码随想录算法训练营第40天|343. 整数拆分、96.不同的二叉搜索树
343. 整数拆分
题目链接:link
文章讲解:link
视频讲解:link
一、做题感受&第一想法
其实第一反应是回溯……但感觉每层的集合都会很繁琐
二、学习文章后收获
1.动态规划思路
-
动规五要素分析
- dp和i的定义:dp[i]指把i拆分后最大乘积(所以dp[1]、dp[0]都没有太大意义,因为0和1拆了乘积也是0)
- 递归公式:
dp[i] = max(j * (i - j) , j * dp[i - j]), 1 <= j < i - 1(j<i-1是为什么?因为j = i-1时,dp[j-i]也就是dp[1]为0,没有意义;而 j*(i-j)也就是(i-1)*1,这和 j=1重复了,所以可以省去j = i-1的讨论!) - 初始化:dp[0] = 0,dp[1] = 0,dp[2] = 1
- 遍历顺序:从前往后
- 手算序列(略)
-
递归公式的说明:求dp[i]可分成两种情况
- 把 i 拆成 j 和 i - j 两个数,总共两个数。
- 把 i 拆成 j 和"和为 i - j 的若干个数",总共大于等于三个数。
class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1,0); //dp[i]:拆分i得到的最大乘积dp[0] = 0;dp[1] = 0; //其实这俩初始化无所谓,因为没有意义dp[2] = 1; // 1*1for(int i = 3;i <= n;i++){for(int j = 1;j < i - 1;j++){dp[i] = max(dp[i],max(j*(i-j),j*dp[i-j]));}}return dp[n];}
};
2.动态规划优化
思路:for循环上的剪枝,剪枝依据是,要想找到乘积最大的拆分方式,需要让拆出来的所有数字尽可能大小相似。所以,对于太大的 j ,可以直接跳过。
故内层for的条件改为 j <= i/2:for (int j = 1; j <= i / 2; j++)
class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) { //here!dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};2.贪心思路
思路:本题也可以用贪心,每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!
此处没有证明,而是直接用了结论。
说明:
if(n == 2) return 1;
if(n == 3) return 2;
if(n == 4) return 4;
剩下的,拆成3的和,直到剩下4或者不足3(也就是前面是一堆3,最后剩下的值<=4即停止,作为最后一个数字)。
class Solution {
public:int integerBreak(int n) {if(n == 1 || n == 0) return 0;if(n == 2) return 1;if(n == 3) return 2;if(n == 4) return 4;int remains = n - 3,result = 3;while(remains > 4){result *= 3;remains -= 3;}result *= remains;return result;}
};
三、过程中遇到的问题
1.多个数取最大
max(a,max(b,c))
96.不同的二叉搜索树
题目链接:link
文章讲解:link
视频讲解:link
一、做题感受&第一想法
- 动规五要素分析
- dp和i的定义:dp[i]指 i 个节点的二叉搜索树共有多少种树型
- 递归公式:
dp[i] += dp[j] * dp[i-j-1], 0 <= j <= i - 1(左子树 j 个节点,右子树 i - j - 1个节点。总树型为 左子树的树型数 乘以 右子树的树型数) - 初始化:dp[0] = 1,dp[1] = 1
- 遍历顺序:从前往后
- 手算序列(略)
class Solution {
public:int numTrees(int n) {vector<int> dp(n+1,0);dp[0] = 1;dp[1] = 1;for(int i = 2;i <= n;i++){ //dp[i]for(int j = 0;j <= i - 1;j++){ //左子树:j,右子树:i-j-1dp[i] += dp[j] * dp[i-j-1]; //递推公式}}return dp[n];}
};
相关文章:

代码随想录算法训练营第40天|343. 整数拆分、96.不同的二叉搜索树
343. 整数拆分 题目链接:link 文章讲解:link 视频讲解:link 一、做题感受&第一想法 其实第一反应是回溯……但感觉每层的集合都会很繁琐 二、学习文章后收获 1.动态规划思路 动规五要素分析 dp和i的定义:dp[i]指把i拆分后最…...

二叉树算法
递归序 每个节点都能回到3次! 相当于2执行完然后返回了代码会往下走,来到3节点 小总结: 也就是4节点先来到自己一次,不会执行if,先调用自己左边的那个函数,但是是null,直接返回。 这个函数执行完了,就会回到自己,调用自己右边的那个函数,结果又是空,又返回,回到…...
 - 4 项目范围管理(高项)》)
【2024年5月备考新增】《软考真题分章练习(答案解析) - 4 项目范围管理(高项)》
点击跳转无答案版 1、() includes the processes required to ensure that the project includes all the work required , and only the work required , to complete the project successfully . Managing the project scope is primarily concerned with defining and con…...

Docker拉取镜像存储不足
在使用Docker时,我们经常遇到一个问题,就是拉取镜像时提示存储空间不足。这是因为Docker在拉取镜像时需要将镜像文件下载到本地存储中,而有时本地存储空间不足以容纳完整的镜像文件。 本文将介绍一些解决这个问题的方法,并提供相…...

JUNIT5+Mockito单元测试
文章目录 1、前言2、Maven依赖2.1 JDK21SpringBoot版本基于3.1.02.2 JDK17SpringBoot版本基于2.2.5.RELEASE 3、业务代码4、单元测试 1、前言 之前写过一篇使用testMe自动生成单元测试用例,使用的是junit4来编写的单元测试用例,目前很多新项目都已经使用…...
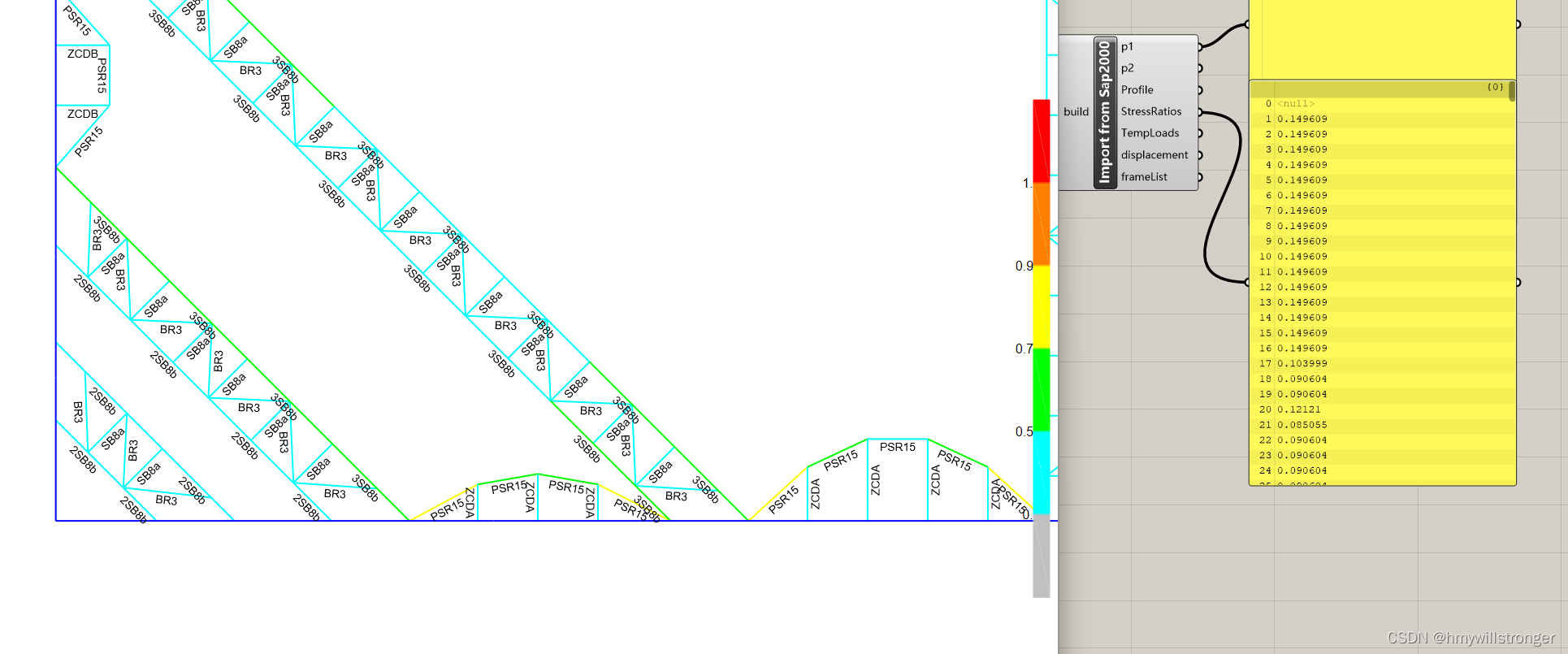
【C#】【SAP2000】读取SAP2000中所有Frame对象的应力比到Grasshopper中
if (build true) {// 连接到正在运行的 SAP2000// 使用 System.Runtime.InteropServices.Marshal.GetActiveObject 方法获取正在运行的 SAP2000 实例cOAPI mySapObject (cOAPI)System.Runtime.InteropServices.Marshal.GetActiveObject("CSI.SAP2000.API.SapObject"…...

一台服务器部署两个独立的mysql实例
🍁博主简介: 🏅云计算领域优质创作者 🏅2022年CSDN新星计划python赛道第一名 🏅2022年CSDN原力计划优质作者 🏅阿里云ACE认证高级工程师 🏅阿里云开发者社区专…...

SpringBoot(Lombok + Spring Initailizr + yaml)
1.Lombok 1.基本介绍 2.应用实例 1.pom.xml 引入Lombok,使用版本仲裁 <!--导入springboot父工程--><parent><artifactId>spring-boot-starter-parent</artifactId><groupId>org.springframework.boot</groupId><version&g…...

数据库基础知识超详细解析~(进阶/复习版)
文章目录 前言一、数据库的操作1.登入数据库2.创建数据库3.显示当前数据库4.使用数据库5.删除数据库 二、常用数据类型三、数据库的约束1约束类型2NULL约束3UNIQUE:唯一约束4DEFAULT:默认值约束5 PRIMARY KEY:主键约束6 FOREIGN KEY:外键约束…...

创建对象的方法有哪些
创建对象的方法主要取决于你使用的编程语言和上下文。下面我将列出一些主流编程语言中创建对象的方法: Python: 使用类定义和__init__方法: pythonclass MyClass: def __init__(self, name): self.name nameobj MyClass("Alice") 1.使用工厂…...

Oracle 10g字符编码
pl/sql developer查询数据时出现乱码,主要检查如下: 1、检查服务器编码 select * from v$nls_parameters;select * from nls_database_parameters;select userenv(language) from dual; 2、查看数据库可用字符集参数设置 select * from v$nls_valid_val…...

掌握抽象基础之20个必备原则,看完你还不会,你打我
抽象基础之20个必备原则 1. 面向对象编程(OOP)中抽象原则背后的基本思想是什么?2.抽象和封装的区别?3.提供一个现实生活中说明抽象的例子4.在编程语言中如何实现抽象?5.定义抽象类6.提供一个抽象类的真实世界场景7.解释…...
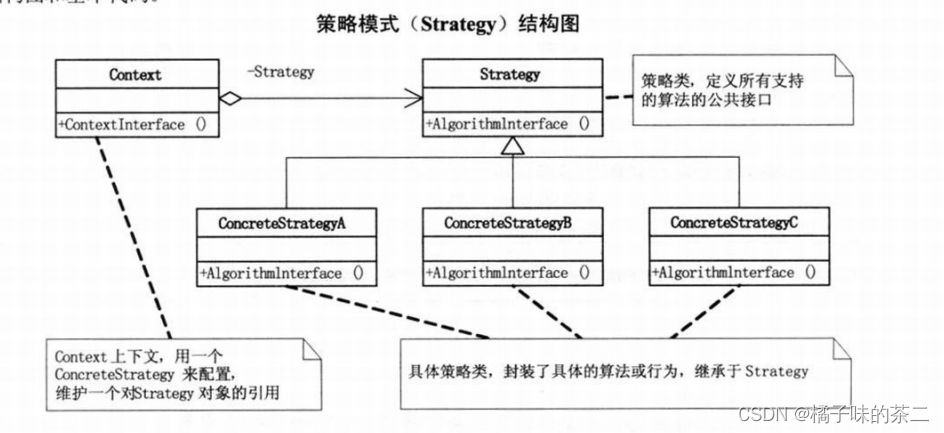
设计模式 -- 2:策略模式
目录 总结部分:策略模式的优点部分代码部分 总结部分: 策略模式和简单工厂模式很像 区别在于 简单工厂模式 需求的是由工程创造的类 去给客户直接答案 而策略模式在于 我有主体 一个主体 根据策略的不同来进行不同的计算 我的主体就负责收钱 然后调度相…...
【快速上手ProtoBuf】proto 3 语法详解
1 🍑字段规则🍑 消息的字段可以⽤下⾯⼏种规则来修饰: singular :消息中可以包含该字段零次或⼀次(不超过⼀次)。 proto3 语法中,字段默认使⽤该规则。repeated :消息中可以包含该…...

人工智能的幽默“失误”
人工智能迷惑行为大赏 随着ChatGPT热度的攀升,越来越多的公司也相继推出了自己的AI大模型,如文心一言、通义千问等。各大应用也开始内置AI玩法,如抖音的AI特效~在使用过程中往往会遇到一些问题,让你不得不怀疑&#x…...

js的异步请求?
在 JavaScript 中,进行异步请求通常涉及到使用 XMLHttpRequest 对象或者更现代的 Fetch API 或 Axios 库。这些工具可以帮助我们向服务器发送请求并在后台获取数据,而不会阻塞页面的其他操作。 下面是一个简单的示例,演示如何使用原生的 XML…...
工具类)
华润对象存储(OBS)工具类
目录 一、备注二、工具类三、对象存储放在内网,如何实现外网访问 一、备注 1、ObjectBasicInfo、ObjectDetailInfo、ResultBody这三个类可自行替换或者去掉 二、工具类 package com.xxx.util;import com.amazonaws.HttpMethod; import com.amazonaws.auth.AWSStat…...

强缓存和协商缓存的区别?
协商缓存和强缓存是 HTTP 缓存机制中的两种不同的策略,用于减少网络请求并提高网页加载速度。它们之间的主要区别在于缓存的验证方式和服务器返回的响应头。 强缓存: 强缓存是基于过期时间(Expires)和缓存标识(Cache…...

ChatGPT提问技巧——对抗性提示
ChatGPT提问技巧——对抗性提示 对抗性提示是一种允许模型生成能够抵御某些类型的攻击或偏差的文本的技术。这种技术可用于训练更健壮、更能抵御某些类型的攻击或偏差的模型。 要在 ChatGPT 中使用对抗性提示,应为模型提供一个提示,该提示的设计应使模…...

openGauss使用BenchmarkSQL进行性能测试(上)
一、前言 本文提供openGauss使用BenchmarkSQL进行性能测试的方法和测试数据报告。 BenchmarkSQL,一个JDBC基准测试工具,内嵌了TPC-C测试脚本,支持很多数据库,如PostgreSQL、Oracle和Mysql等。 TPC-C是专门针对联机交易处理系统…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
