<个人笔记>数论
1.快速幂
(1)求解问题:
给定 n组 ai,bi,pi求 aibi mod pi 的值。
(2)主要思想:任何一个数(b),可以被 n 个 2k 相加获得。
即 b= 2k1 + 2k2 + 2k3 + … + 2logb。
快速幂模板:
typedef long long LL;LL qmi(int a,int b,int p){LL res = 1;while(b){if(b & 1) res = res * a % p;a = a * (LL)a % p;b >>= 1;}return res;
}
逆元
(1)求解问题:对于a / b mod p的值:
将除法改为乘法; 例如 求 (A / B) %p ;在B的值非常大的情况下,B作为除数,极有可能会爆精度;除数不能太大;所以我们可以把他转化为乘法来解决;
(2)主要思想:
费马小定理:对于bp-1(mod p) = 1 恒成立。且 逆元:b * b-1 = 1 (mod p)
所以 b 的逆元 b-1 为 bp-2.
可以用快速幂来求:
b^-1^ = qmi(b,p-2,p);
相关文章:

<个人笔记>数论
1.快速幂 (1)求解问题: 给定 n组 ai,bi,pi求 aibi mod pi 的值。 (2)主要思想:任何一个数(b),可以被 n 个 2k 相加获得。 即 b 2k1 2k2 2k3 … 2logb。 快速幂模板: typedef long long LL;LL qmi(int a,int b,int p){LL re…...

CMS垃圾收集
初始标记 需要暂停所有的其他线程,但这个阶段会很快完成。它的目的是标记所有的根对象,以及被根对象直接引用的对象,以及年轻代指向老年代的对象,不会遍历对象关系,单线程执行。 并发标记阶段 不需要暂停应用线程&a…...

Incorrect DECIMAL value: ‘0‘ for column ‘‘ at row -1
用mysql插入数据的时候,报了上面的错误。 语句类似:INSERT INTO t_aa(c1,c2,c3,a1,a2,a3) SELECT t1,t2,t3,b1,b2,b3 FROM ( SELECT, t1,t2,t3 cast(ifnull(d1,0)as decimal(8,1) b1, cast(ifnull(d2,0) as decimal(8,1) b2, …...

Vue3组件通信的方式
1、父给子传 — props 父组件 <template><h1>父</h1><Son :value"number" /><button click"add">点我加1</button> </template><script setup> import Son from ./son.vue;import { ref } from vue; le…...
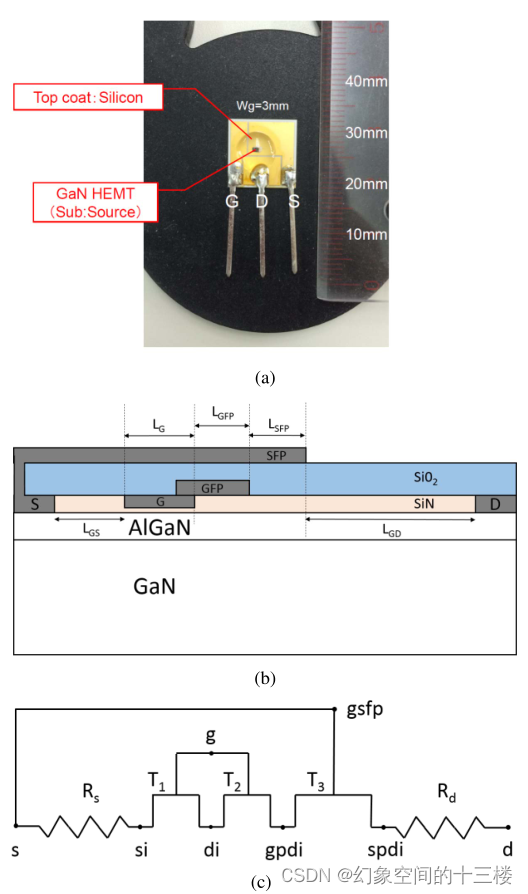
双场板功率型GaN HEMT中用于精确开关行为的电容建模
来源:Capacitance Modeling in Dual Field-Plate Power GaN HEMT for Accurate Switching Behavior (TED 16年) 摘要 本文提出了一种基于表面电势的紧凑模型,用于描述具有栅极和源极场板(FP)结构的AlGaN/GaN高电子迁移率晶体管(…...
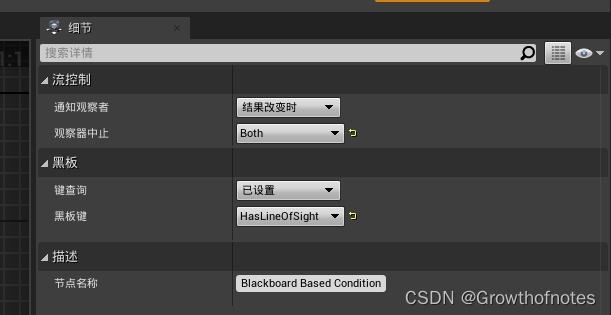
UE4_AI_行为树_行为树快速入门指南
声明:学习笔记。 在 行为树快速入门指南 中,你将学会如何创建一个敌方AI,该AI看到玩家后会做出反应并展开追逐。当玩家离开视线后,AI将在几秒钟后(这可根据你的需求进行调整)放弃追逐,并在场景中…...

c++ 面试100个题目中的编程题目
88、下列程序的运行结果是? #include <stdlib.h> #include <stdio.h> #include <string.h> #include <iostream> const char* str = "vermeer"; using namespace std; int main(){ const char* pstr = str;cout << "The add…...

C++初阶:类与对象(尾篇)
目录 1. 构造函数与初始化列表1.1 对象的创建与构造函数的初始化1.2 初始化列表及构造函数存在的意义1.3 explicit关键字与构造函数的类型转换 2. static成员变量与static成员函数2.1 static成员变量2.2 static成员函数 3. 日期类流插入操作符的重载与友元3.1 友元3.2 友元函数…...

Spring状态机简单实现
一、什么是状态机 状态机,又称有限状态自动机,是表示有限个状态以及在这些状态之间的转移和动作等行为的计算模型。状态机的概念其实可以应用的各种领域,包括电子工程、语言学、哲学、生物学、数学和逻辑学等,例如日常生活中的电…...
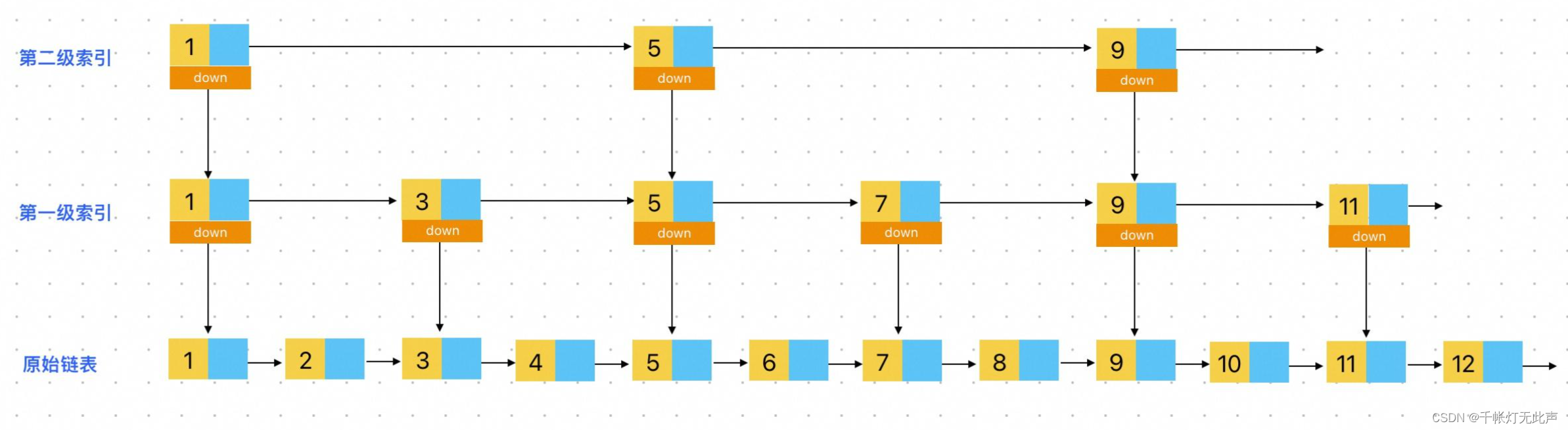
WebServer -- 面试题(下)
👂 夏风 - Gifty - 单曲 - 网易云音乐 目录 🌼前言 🎂面试题(下) 4)HTTP报文解析 为什么要用状态机 状态转移图画一下 https 协议为什么安全 https 的 ssl 连接过程 GET 和 POST 的区别 5)数据库注册登录 登…...
企业微信如何接入第三方应用?
1.登录企业微信管理后台:https://work.weixin.qq.com/wework_admin 2.点击创建应用; 3. 此时可以看到已经创建好的应用,并且生成应用的唯一id(agentId) 4. 第三方应用申请域名 (举例&…...

JAVA后端编码的主键字段存储为什么倾向于使用雪花算法
1.背景 最近有人问,什么是雪花算法,为什么使用雪花算法不使用数据库UUID,基于此,写一个说明。 2.简介 (1)雪花算法,英文名为snowflake,翻译过来就是是雪花,所以叫雪花…...
Rust 深度学习库 Burn
一、概述 Burn 它是一个新的综合动态深度学习框架,使用 Rust 构建的,以极高的灵活性、计算效率和可移植性作为其主要目标。 Rust Burn 是一个以灵活性、高性能和易用性为核心设计原则工具,主打就是灵活性 、高性能 及易用性。 二、Rust B…...

C语言-存储期2.0
静态存储期 在数据段中分配的变量,统统拥有静态存储期,因此也都被称为静态变量。这里静态的含义,指的是这些变量的不会因为程序的运行而发生临时性的分配和释放,它们的生命周期是恒定的,跟整个程序一致。 静态变量包含…...

计算机网络面经八股-HTTP请求报文和响应报文的格式?
请求报文格式: 请求行(请求方法URI协议版本)请求头部空行请求主体 请求行:GET /sample.jsp HTTP/1.1 表示使用 GET 方法请求 /sample.jsp 资源,并使用 HTTP/1.1 协议。请求头部:包含多个字段,…...
报依赖库版本过低错误)
Ubuntu 18.04安装最新版Visual Studio Code(VS Code)报依赖库版本过低错误
Ubuntu 18.04安装最新版Visual Studio Code(VS Code)报依赖库版本过低错误 1. 问题描述2. 解决方案2.1 修复之前安装的错误2.2 安装VS Code 1.85.2 3. 原因分析 1. 问题描述 在Ubuntu 18.04系统上安装VS Code ≥ v1.86.2(测试到v1.87.1&…...

Android NDK入门:在应用中加入C和C++的力量
目录 编辑 引 NDK的设计目的 与Java/Kotlin的结合 使用场景 开发流程 设置项目以支持NDK 编写本地代码 使用JNI连接本地代码和Java/Kotlin代码 编译和运行你的应用 附 引 自诩方向是android方向的移动端开发工程师,却从来没有真正仔细了解过NDK&#…...
)
2024年华为OD机试真题-田忌赛马-Java-OD统一考试(C卷)
题目描述: 给定两个只包含数字的数组a,b,调整数组 a 里面数字的顺序,使得尽可能多的 a[i] >b[i]。数组 a和 b 中的数字各不相同。 输出所有可以达到最优结果的 a 数组的数量 输入描述: 输入的第一行是数组 a 中的数字,其中只包含数字,每两个数字之间相隔一个空格,a…...
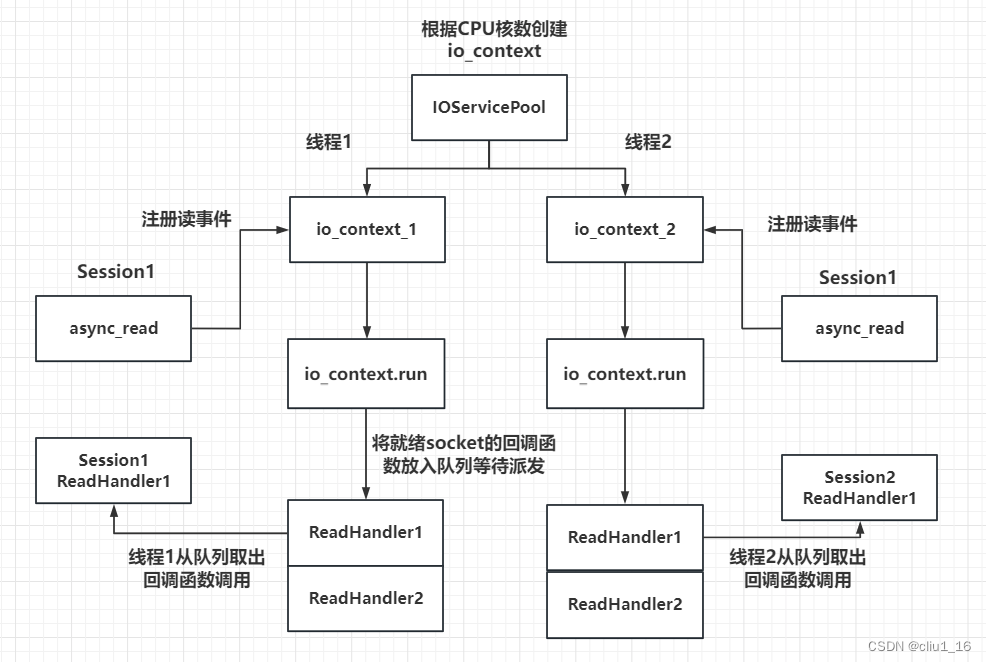
C++ 网络编程学习五
C网络编程学习五 网络结构的更新单例模式懒汉单例模式饿汉单例模式懒汉式指针智能指针设计单例类 服务器优雅退出asio的多线程模型IOServiceasio多线程IOThreadPoolepoll 和 iocp的一些知识点 网络结构的更新 asio网络层,会使用io_context进行数据封装,…...
案例分析篇05:数据库设计相关28个考点(9~16)(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章推荐: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html 【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例分析篇-…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
