Java必须掌握的二叉堆知识点(含面试大厂题含源码)
二叉堆是一种常用的优先队列数据结构,广泛应用于各种场景,比如任务调度、带权图的最短路径算法(如Dijkstra算法)等。在Java面试中,了解二叉堆的基本概念、实现方式和操作是非常重要的。下面是一些关于二叉堆的关键知识点,这些内容会帮助你在面试大厂时更好地展示你的技术实力。
二叉堆的定义
二叉堆是一种完全二叉树,它可以分为两种类型:
- 最小堆:父节点的值总是小于或等于其任意子节点的值。
- 最大堆:父节点的值总是大于或等于其任意子节点的值。
二叉堆的性质
- 结构性质:二叉堆是一种完全二叉树,这意味着除了最后一层外,每一层都被完全填满,并且最后一层的所有节点都尽可能地集中在左边。
- 堆序性质:在最小堆中,每个节点的值都小于或等于其子节点的值;在最大堆中,每个节点的值都大于或等于其子节点的值。
二叉堆的存储
二叉堆通常使用数组来存储,不需要使用节点指针。给定一个索引为i的节点:
- 它的父节点的索引是
(i-1)/2(对于i>0)。 - 它的左子节点的索引是
2*i + 1。 - 它的右子节点的索引是
2*i + 2。
二叉堆的基本操作
- 插入操作:新元素被加到堆的末尾,然后向上调整(上浮)以恢复堆的性质。
- 删除操作(最小堆为例):删除堆顶元素,通常是堆中最小的元素。然后将最后一个元素移动到堆顶,之后向下调整(下沉)以恢复堆的性质。
Java中的二叉堆实现
虽然Java标准库中没有直接提供二叉堆的实现,但是PriorityQueue类提供了基于优先队列的实现,底层就是使用二叉堆(默认是最小堆)实现的。PriorityQueue提供了如下几个关键方法:
add(E e)/offer(E e):将指定的元素插入此优先队列。remove()/poll():检索并删除此队列的头部,即最小元素。element()/peek():检索但不删除此队列的头部,即最小元素。
二叉堆的应用
- 优先队列的实现:使用二叉堆可以高效地实现优先队列,支持插入和删除最小元素的操作。
- 堆排序:通过构建最大堆(或最小堆),可以实现堆排序算法,这是一种原地排序算法,但不是稳定的。
- 图算法中的应用:在很多图算法中,如Dijkstra和Prim算法,优先队列(通常通过二叉堆实现)被用来高效地选择下一个要处理的节点。
掌握这些二叉堆的基础知识点对于Java面试是非常有帮助的,尤其是当你被要求手动实现数据结构或解决与之相关的算法问题时。在准备面试时,确保你理解这些概念,并且能够在需要时快速实现它们。下面是三道常见的面试题目,它们涵盖了二叉树、字符串处理以及动态规划等不同的领域,每个题目都附上了Java的实现代码。
题目1:验证二叉搜索树(Binary Search Tree, BST)
问题描述:给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
Java解答:
public class ValidateBinarySearchTree {public boolean isValidBST(TreeNode root) {return validate(root, Long.MIN_VALUE, Long.MAX_VALUE);}private boolean validate(TreeNode node, long min, long max) {if (node == null) return true;if (node.val <= min || node.val >= max) return false;return validate(node.left, min, node.val) && validate(node.right, node.val, max);}public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) { val = x; }}
}
题目2:最长回文子串
问题描述:给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s
的最大长度为 1000。
示例:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
Java解答:
public class LongestPalindromicSubstring {public String longestPalindrome(String s) {if (s == null || s.length() < 1) return "";int start = 0, end = 0;for (int i = 0; i < s.length(); i++) {int len1 = expandAroundCenter(s, i, i);int len2 = expandAroundCenter(s, i, i + 1);int len = Math.max(len1, len2);if (len > end - start) {start = i - (len - 1) / 2;end = i + len / 2;}}return s.substring(start, end + 1);}private int expandAroundCenter(String s, int left, int right) {while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {left--;right++;}return right - left - 1;}
}
题目3:爬楼梯
问题描述:假设你正在爬楼梯。需要 n 步你才能到达顶部。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到顶部呢?
注意:给定 n 是一个正整数。
示例:
输入: 2
输出: 2
解释: 有两种方法可以爬到顶部。
1. 1 步 + 1 步
2. 2 步
Java解答:
public class ClimbingStairs {public int climbStairs(int n) {if (n == 1) return 1;int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}
这些题目从基本的数据结构到算法思想都有所涵盖,是面试中非常典型的题目。掌握这些题目的解法不仅能帮助你在面试中脱颖而出,同时也能提升你解决实际问题的能力。在准备面试时,理解这些问题的核心思想和解决策略是非常重要的。
相关文章:
)
Java必须掌握的二叉堆知识点(含面试大厂题含源码)
二叉堆是一种常用的优先队列数据结构,广泛应用于各种场景,比如任务调度、带权图的最短路径算法(如Dijkstra算法)等。在Java面试中,了解二叉堆的基本概念、实现方式和操作是非常重要的。下面是一些关于二叉堆的关键知识…...

[Java、Android面试]_03_java内存管理:虚拟内存、堆、垃圾回收
本人今年参加了很多面试,也有幸拿到了一些大厂的offer,整理了众多面试资料,后续还会分享众多面试资料,感兴趣的朋友可收藏关注, 现分享如下: 文章目录 1. Java虚拟机运行时数据区2. Java堆3. 垃圾回收3.1 如…...
PTA题解 --- 求整数段和(C语言)
今天是PTA题库解法讲解的第二天,接下来讲解求整数段和,题目如下: 为了解决这个问题,你可以遵循以下的思路: 1. 读取输入的两个整数A和B。 2. 使用一个for循环,从A遍历到B。 3. 在循环中,打印当…...

virsh管理虚拟机的命令行工具
virsh是一个管理虚拟机的命令行工具,提供了丰富的命令来查看、创建、管理虚拟机。以下是一些常用的virsh命令: 查看帮助和版本: virsh --help:查看virsh命令的帮助信息。virsh -version:查看virsh的版本信息。 查看虚…...

数据集成平台选型建议
一 数据集成介绍 数据集成平台是一种用于管理和协调数据流动的软件工具或服务。它的主要目标是将来自多个不同数据源的数据整合到一个统一的、易于访问和分析的数据存储库中。这些数据源可以包括数据库、云应用、传感器、日志文件、社交媒体等等。数据集成平台的关键任务是确保…...

Centos8安装Docker,使用阿里云源
一、前期准备 1.关闭防火墙,SELINUX systemctl stop firewalld.service systemctl disable firewalld.service setenforce 0 sed -i "s/SELINUXenforcing/SELINUXdisabled/g" /etc/selinux/config查看状态 systemctl status firewalld systemctl status…...

FFmpeg概念和简单使用
FFmpeg是一个开源的跨平台多媒体处理工具套件,包含了用于处理音频、视频和图像的各种工具、库和命令行程序。它由一个主要的命令行工具ffmpeg和一系列相关工具组成,可以执行各种各样的多媒体操作。以下是FFmpeg中一些重要的概念: 音频、视频和…...

OJ_最长公共子序列
题干 C实现 #include <iostream> #include <stdio.h> #include <algorithm> using namespace std;int dp[1002][1002];int main() {int n,m;char s1[1001];char s2[1001];scanf("%d%d",&n,&m);scanf("%s%s",s1,s2);//dp[i][j]是…...

SpringBoot拦截器获取token用户对象优雅地传递到Controller层
项目场景: SpringBoot拦截器获取token用户对象优雅地传递到Controller层 问题描述 后端有许多接口都需要请求中携带有正确的Token,这时采用拦截器来验证token,但是每个接口都还是需要解析一遍token,浪费资源,不免显得…...

从零开始学HCIA之SDN03
1、VXLAN相关概念 (1)NVE(Network Virtual Edge),网络虚拟化边界,是运行VXLAN的设备,其实体是一种虚拟逻辑接口,负责VXLAN数据的封装和解封装,其主要参数包括源VTEP以及…...

C语言深度理解之——结构体内存对齐
前言: 在C语言中,结构体(struct)是一种用户自定义的数据类型,可以包含不同类型的数据成员。在定义结构体时,编译器会根据平台的要求对结构体的内存进行对齐,以提高内存访问的效率。结构体内存对…...

LeetCode 热题 100 | 回溯(二)
目录 1 39. 组合总和 2 22. 括号生成 3 79. 单词搜索 菜鸟做题,语言是 C,感冒快好版 关于对回溯算法的理解请参照我的上一篇博客; 在之后的博客中,我将只分析回溯算法中的 for 循环。 1 39. 组合总和 题眼:c…...

混合内容错误https中加载了http
一、遇到问题 iframe嵌套时,混合内容错误https中加载了http,但是已经确认了ifreme中是https的,最后发现在/my/edit?applyid1改为/my/edit/?applyid1,加了一个斜杠,直接解决了 /my/edit是vue页面,其他页…...
游戏免费下载平台模板源码
功能介绍 此游戏网站模板源码是专门为游戏下载站而设计的,旨在为网站开发者提供一个高效、易于维护和扩展的解决方案。 特点: 响应式设计:我们的模板可以自适应不同设备屏幕大小,从而为不同平台的用户提供最佳的浏览体验。 …...

鸿蒙视频播放的实现
文章目录 前言播放效果视频播放的实现总结 一、前言 现在市面上很多应用都跟视频有关,那么在鸿蒙系统上怎么来播放视频呢,今天就讲解视频播放控件,让你也能快速地进行视频播放功能开发。 最后呢,我会提供一个鸿蒙中涉及的主要…...

QT----计算器
目录 1 搭建标准界面2、 逻辑编写2.1 初始化 github链接:基于qt的计算器 更多内容可以点击这里查看个人博客:个人博客 1 搭建标准界面 按照下图搭设界面 修改样式让这计算器看起来更像一点,同时对按钮分组进行样式编辑,添加字符…...
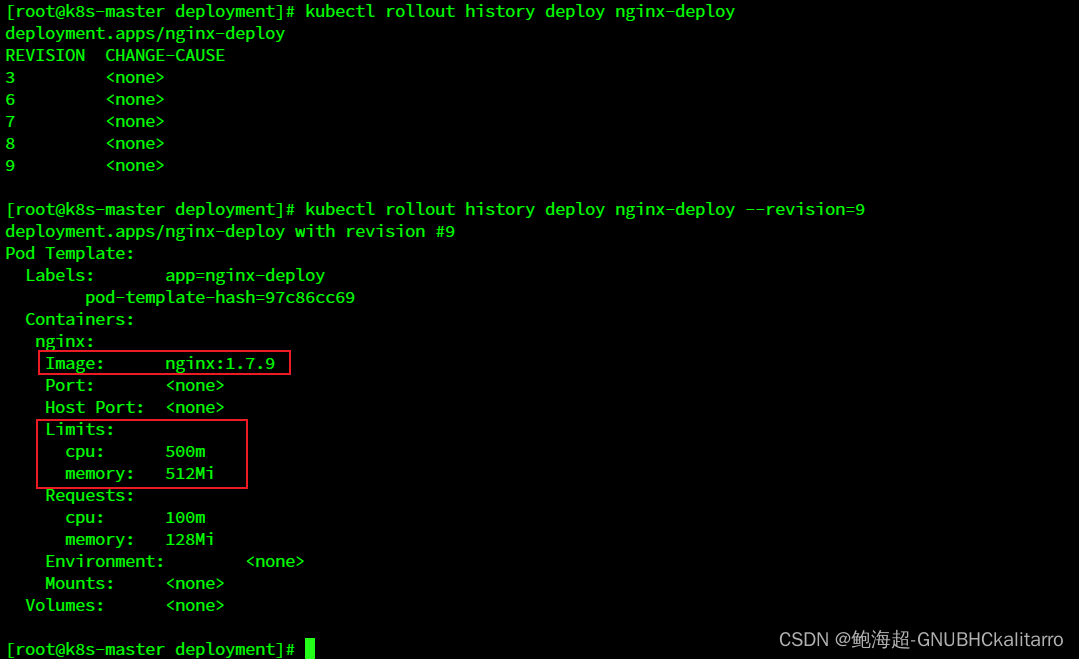
Linux:kubernetes(k8s)Deployment的操作(13)
创建deployment 命令 kubectl create deploy nginx-deploy --imagenginx:1.7.9 再去使用以下命令分别查询 ubectl get deploy kubectl get replicaset kubectl get pod 他是一个层层嵌套的一个关系 首先是创建了一个 deploy 里面包含着replicaset replicaset里面含有…...

20240619-James-快速鸟瞰并发编程, 呕心沥血整理的架构技术(第3篇)
接着第1, 2篇后,我们继续来跟进一下并发编程的其它内容,如下: 第9节 java.util.concurrent包 线程池 线程池的核心接口是ExecutorService。java.util.concurrent还提供了一个静态工厂类Executors,其中包含用于创建配置线程池的…...

C语言——详解字符函数和字符串函数(一)
Hi,铁子们好呀!今天博主来给大家更一篇C语言的字符函数和字符串函数~ 具体讲的内容如下: 文章目录 🎆1.字符分类函数💯💯⏩1.1 什么是字符分类函数的?💯💯⏩1.2 字符函数的类型有哪…...

三款内衣洗衣机的顶级较量:希亦、小吉、由利,谁才是性价比之王?
洗衣机在我们的生活中可谓是非常常见的了,几乎每家每户都具备着一台。即便是有洗衣机,也有不少人不会将自己我贴身衣物直接扔在洗衣机里清洗,而是会自己手工手洗。这跟我们传统上的观念有很大的关系,认为把内衣、内裤等贴身衣物放…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
