【强化学习】强化学习数学基础:随机近似理论与随机梯度下降
强化学习数学基础:随机近似理论与随机梯度下降
- Stochastic Approximation and Stochastic Gradient Descent
- 举个例子
- Robbins-Monro algorithm
- 算法描述
- 举个例子
- 收敛性分析
- 将RM算法用于mean estimation
- Stochastic gradient descent
- 算法描述
- 示例和应用
- 收敛性分析
- 收敛模式
- 一个确定性公式
- BGD, MBGD和SGD
- 总结
- 内容来源
Stochastic Approximation and Stochastic Gradient Descent
举个例子
首先回顾mean estimation:
- 考虑一个random variable X。
- 目标是估计E[X]\mathbb{E}[X]E[X]
- 假设已经有了一系列随机独立同分布的样本{xi}i=1N\{x_i\}_{i=1}^N{xi}i=1N
- X的expection可以被估计为E[X]≈xˉ:=1N∑i=1Nxi\mathbb{E}[X]\approx \bar{x}:=\frac{1}{N}\sum_{i=1}^N x_iE[X]≈xˉ:=N1i=1∑Nxi
已经知道这个估计的基本想法是Monte Carlo estimation,以及xˉ→E\bar{x}\rightarrow \mathbb{E}xˉ→E,随着N→∞N\rightarrow \inftyN→∞。这里为什么又要关注mean estimation,那是因为在强化学习中许多value被定义为means,例如state/action value。
新的问题:如何计算mean barxbar{x}barx:E[X]≈xˉ:=1N∑i=1Nxi\mathbb{E}[X]\approx \bar{x}:=\frac{1}{N}\sum_{i=1}^N x_iE[X]≈xˉ:=N1i=1∑Nxi
我们有两种方式:
- 第一种方法:简单地,收集所有样本,然后计算平均值。但是该方法的缺点是如果样本是一个接一个的被收集,那么就必须等待所有样本收集完成才能计算
- 第二种方法:可以克服第一种方法的缺点,用一种incremental(增量式)和iterative(迭代式)的方式计算average。
具体地,假设wk+1=1k∑i=1kxi,k=1,2,...w_{k+1}=\frac{1}{k}\sum_{i=1}^k x_i, k=1,2,...wk+1=k1i=1∑kxi,k=1,2,...然后有wk=1k−1∑i=1k−1xi,k=2,3,...w_k=\frac{1}{k-1}\sum_{i=1}^{k-1} x_i, k=2,3,...wk=k−11i=1∑k−1xi,k=2,3,...,我们要建立wkw_kwk和wk+1w_{k+1}wk+1之间的关系,用wkw_kwk表达wk+1w_{k+1}wk+1:wk+1=1k∑i=1kxi=1k(∑i=1k−1xi+xk)=1k((k−1)wk+xk)=wk−1k(wk−xk)w_{k+1}=\frac{1}{k}\sum_{i=1}^k x_i=\frac{1}{k}(\sum_{i=1}^{k-1}x_i+x_k)=\frac{1}{k}((k-1)w_k+x_k)=w_k-\frac{1}{k}(w_k-x_k)wk+1=k1i=1∑kxi=k1(i=1∑k−1xi+xk)=k1((k−1)wk+xk)=wk−k1(wk−xk)因此,获得了如下的迭代算法:wk+1=wk−1k(wk−xk)w_{k+1}=w_k-\frac{1}{k}(w_k-x_k)wk+1=wk−k1(wk−xk)
我们使用上面的迭代算法增量式地计算x的mean:
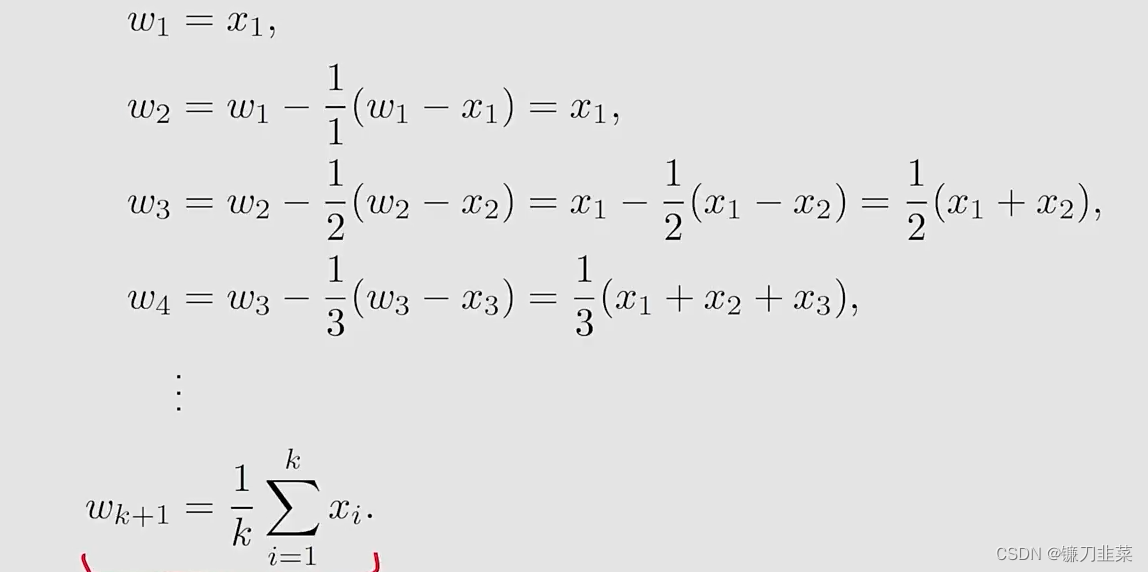
这样就得到了一个求平均数的迭代式的算法。算法的优势是在第k步的时候不需要把前面所有的xix_ixi全部加起来再求平均,可以在得到一个样本的时候立即求平均。另外这个算法也代表了一种增量式的计算思想,在最开始的时候因为kkk比较小,wk≠E[X]w_k\ne \mathbb{E}[X]wk=E[X],但是随着获得样本数的增加,估计的准确度会逐渐提高,也就是wk→E[X]as k→Nw_k\rightarrow \mathbb{E}[X] \text{ as } k\rightarrow Nwk→E[X] as k→N。
更进一步地,将上述算法用一个更泛化的形式表示为:wk+1=wk−αk(wk−xk)w_{k+1}=w_k-\alpha_k(w_k-x_k)wk+1=wk−αk(wk−xk),其中1/k1/k1/k被替换为αk>0\alpha_k >0αk>0。
- 该算法是否会收敛到mean E[X]\mathbb{E}[X]E[X]?答案是Yes,如果{αk}\{\alpha_k\}{αk}满足某些条件的时候
- 该算法也是一种特殊的SA algorithm和stochastic gradient descent algorithm
Robbins-Monro algorithm
算法描述
Stochastic approximation (SA):
- SA代表了一大类的stochastic iterative algorithm,用来求解方程的根或者优化问题。
- 与其他求根相比,例如gradient-based method, SA的强大之处在于:它不需要知道目标函数的表达式,也不知道它的导数或者梯度表达式。
Robbins-Monro (RM) algorithm:
- This is a pioneering work in the field of stochastic approximation.
- 著名的stochastic gradient descent algorithm是RM算法的一个特殊形式。
- It can be used to analyze the mean estimation algorithms introduced in the beginning。
举个例子
问题声明:假设我们要求解下面方程的根g(w)=0g(w)=0g(w)=0,其中w∈Rw\in \mathbb{R}w∈R是要求解的变量,g:R→Rg:\mathbb{R}\rightarrow \mathbb{R}g:R→R是一个函数.
- 许多问题最终可以转换为这样的求根问题。例如,假设J(w)J(w)J(w)是最小化的一个目标函数,然后,优化问题被转换为g(w)=∇wJ(w)=0g(w)=\nabla_w J(w)=0g(w)=∇wJ(w)=0
- 另外可能面临g(w)=cg(w)=cg(w)=c,其中ccc是一个常数,这样也可以将其转换为上述等式,通过将g(w)−cg(w)-cg(w)−c写为一个新的函数。
那么如何求解g(w)=0g(w)=0g(w)=0?
- 如果ggg的表达式或者它的导数已知,那么有许多数值方法可以求解
- 如果函数ggg的表达式是未知的?例如the function由一个artificial neural network表示
这样的问题可以使用Robbins-Monro(RM)算法求解:wk+1=wk−akg~(wk,ηk),k=1,2,3,...w_{k+1}=w_k-a_k\tilde{g}(w_k, \eta_k), k=1,2,3,...wk+1=wk−akg~(wk,ηk),k=1,2,3,...其中
- wkw_kwk是root的第k次估计
- g~(wk,ηk)=g(wk)+ηk\tilde{g}(w_k,\eta_k)=g(w_k)+\eta_kg~(wk,ηk)=g(wk)+ηk是第k次带有噪声的观测
- aka_kak是一个positive coefficient
函数g(w)g(w)g(w)是一个black box!也就是说该算法依赖于数据:
- 输入序列:{wk}\{w_k\}{wk}
- 噪声输出序列:{g~(wk,ηk)}\{\tilde{g}(w_k,\eta_k)\}{g~(wk,ηk)}
这里边的哲学思想:不依赖model,依靠data!这里的model就是指函数的表达式。
收敛性分析
为什么RM算法可以找到g(w)=0g(w)=0g(w)=0的解?
首先给出一个直观的例子:
- g(w)=tanh(w−1)g(w)=tanh(w-1)g(w)=tanh(w−1)
- g(w)=0g(w)=0g(w)=0的true root是w∗=1w*=1w∗=1
- 初始值:w1=2,ak=1/k,ηk=0w_1=2, a_k=1/k, \eta_k=0w1=2,ak=1/k,ηk=0(为简单起见,不考虑噪音)
在本例中RM算法如下:wk+1=wk−akg(wk)w_{k+1}=w_k-a_kg(w_k)wk+1=wk−akg(wk)
当ηk=0\eta_k=0ηk=0的时候g~(wk,ηk)=g(wk)\tilde{g}(w_k, \eta_k)=g(w_k)g~(wk,ηk)=g(wk)。
模拟仿真结果:wkw_kwk收敛到true root w∗=1w*=1w∗=1。

直观上:wk+1w_{k+1}wk+1比wkw_kwk更接近于w∗w*w∗
- 当wk>w∗w_k > w*wk>w∗,有g(wk)>0g(w_k)>0g(wk)>0,那么wk+1=wk−akg(wk)<wkw_{k+1}=w_k-a_kg(w_k) < w_kwk+1=wk−akg(wk)<wk,因此wk+1w_{k+1}wk+1比wkw_kwk更接近于w∗w*w∗
- 当wk<w∗w_k < w*wk<w∗,有g(wk)<0g(w_k)<0g(wk)<0,那么wk+1=wk−akg(wk)>wkw_{k+1}=w_k-a_kg(w_k) > w_kwk+1=wk−akg(wk)>wk,因此wk+1w_{k+1}wk+1比wkw_kwk更接近于w∗w*w∗
上面的分析是基于直观的,但是不够严格。一个严格收敛的结果如下:

在RM算法中,如果上面的条件满足,那么wkw_kwk就会收敛到w∗w*w∗,w∗w*w∗就是g(w)=0g(w)=0g(w)=0的一个解。第一个条件是关于g(w)的梯度要求,第二个条件是关于aka_kak系数的要求,第三个条件是关于这个ηk\eta_kηk,就是测量误差的要求。
这三个条件的解释:
- 条件1:0<c1≤∇kg(w)≤c20<c_1\le\nabla _k g(w)\le c_20<c1≤∇kg(w)≤c2对于所有的www

- 条件2:∑k=1∞ak=∞\sum_{k=1}^\infty a_k=\infty∑k=1∞ak=∞且∑k=1∞ak2<∞\sum_{k=1}^\infty a_k^2< \infty∑k=1∞ak2<∞

- 条件3:E[ηk∣Hk]=0\mathbb{E}[\eta _k|\mathcal{H}_k]=0E[ηk∣Hk]=0并且E[ηk2∣Hk]<∞\mathbb{E}[\eta _k^2|\mathcal{H}_k]<\inftyE[ηk2∣Hk]<∞
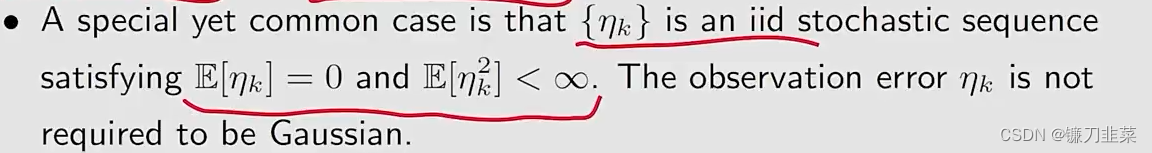
对第二个条件进行讨论:∑k=1∞ak2<∞, ∑k=1∞ak=∞\sum_{k=1}^\infty a_k^2< \infty \text{ , } \sum_{k=1}^\infty a_k=\inftyk=1∑∞ak2<∞ , k=1∑∞ak=∞
- 首先:∑k=1∞ak2<∞\sum_{k=1}^\infty a_k^2< \infty∑k=1∞ak2<∞表明随着k→∞k\rightarrow \inftyk→∞,ak→0a_k\rightarrow 0ak→0
- 为什么这个条件重要呢?
因为wk+1−wk=−akg~(wk,ηk)w_{k+1}-w_k=-a_k\tilde{g}(w_k, \eta_k)wk+1−wk=−akg~(wk,ηk)- 如果ak→0a_k\rightarrow 0ak→0,那么akg~(wk,ηk)→0a_k\tilde{g}(w_k, \eta_k)\rightarrow 0akg~(wk,ηk)→0,因此wk+1−wk→0w_{k+1}-w_k\rightarrow 0wk+1−wk→0
- we need the fact that wk+1−wk→0w_{k+1}-w_k\rightarrow 0wk+1−wk→0 如果wkw_kwk最终收敛
- 如果wk→w∗w_k\rightarrow w*wk→w∗,那么g(wk)→0g(w_k)\rightarrow 0g(wk)→0和g~(wk,ηk)\tilde{g}(w_k, \eta_k)g~(wk,ηk)由ηk\eta_kηk确定。
- 第二,∑k=1∞ak=∞\sum_{k=1}^\infty a_k=\infty∑k=1∞ak=∞表明aka_kak不应当太快收敛到0.
- 为什么这个条件重要呢?
- 根据w2=w1−a1g~(w1,η1)w_2=w_1 - a_1\tilde{g}(w_1, \eta_1)w2=w1−a1g~(w1,η1), w3=w2−a2g~(w2,η2)w_3=w_2 - a_2\tilde{g}(w_2, \eta_2)w3=w2−a2g~(w2,η2), …, wk+1=wk−akg~(wk,ηk)w_{k+1}=w_k - a_k\tilde{g}(w_k, \eta_k)wk+1=wk−akg~(wk,ηk)得出w∞−w1=∑k=1∞akg~(wk,ηk)w_\infty-w_1=\sum_{k=1}^{\infty} a_k\tilde{g}(w_k, \eta_k)w∞−w1=k=1∑∞akg~(wk,ηk)。假定w∞=w∗w_\infty=w*w∞=w∗。如果∑k=1∞ak<∞\sum_{k=1}^\infty a_k<\infty∑k=1∞ak<∞,那么∑k=1∞akg~(wk,ηk)\sum_{k=1}^\infty a_k\tilde{g}(w_k, \eta_k)∑k=1∞akg~(wk,ηk)可能是有界的。然后,如果初始猜测w1w_1w1任意选择远离w∗w*w∗,那么上述等式可能是不成立的(invalid)。
那么问题来了,什么样的ak{a_k}ak能够满足这样两个条件呢?∑k=1∞ak=∞\sum_{k=1}^\infty a_k=\infty∑k=1∞ak=∞且∑k=1∞ak2<∞\sum_{k=1}^\infty a_k^2< \infty∑k=1∞ak2<∞
一个典型的序列是ak=1ka_k=\frac{1}{k}ak=k1
- 在数学上limn→∞(∑k=1n1n−lnn)=k\lim _{n\rightarrow \infty}(\sum _{k=1}^n\frac{1}{n}-\ln n) = kn→∞lim(k=1∑nn1−lnn)=k其中k≈0.577k\approx 0.577k≈0.577,称为
Euler-Mascheroni常数(也称为Euler常数) - 另一个数学上的结论是:∑k=1∞1k2=π26<∞\sum _{k=1}^\infty\frac{1}{k^2}=\frac{\pi^2}{6}<\inftyk=1∑∞k21=6π2<∞极限∑k=1∞\sum _{k=1}^\infty∑k=1∞在数论中也有一个特定的名字:
Basel problem。
如果上面三个条件不满足,则RM算法将不再工作,例如:

在许多RL算法中,aka_kak经常选择一个非常小的常数(sufficiently small constant),尽管第二个条件不满足,但是该RM算法仍然可以工作。
将RM算法用于mean estimation
回顾本文最初的mean estimation算法wk+1=wk−αk(wk−xk)w_{k+1}=w_k-\alpha_k(w_k-x_k)wk+1=wk−αk(wk−xk)
我们知道:
- 如果αk=1/k\alpha_k=1/kαk=1/k,那么wk+1=1/k∑i=1kxiw_{k+1}=1/k\sum_{i=1}^k x_iwk+1=1/k∑i=1kxi
- 如果αk\alpha_kαk不是1/k1/k1/k,收敛性没办法分析。
现在我们证明这个算法是一个特殊的RM算法,它的收敛性就能够得到了。
1)考虑一个函数g(w)≐w−E[X]g(w)\doteq w-\mathbb{E}[X]g(w)≐w−E[X]我们的目标是求解g(w)=0g(w)=0g(w)=0,这样,我们就可以得到E[X]\mathbb{E}[X]E[X]
2)我们不知道X,但是可以对X进行采样,因此我们得到的观察是g~(w,x)≐w−x\tilde{g}(w, x)\doteq w-xg~(w,x)≐w−x,注意
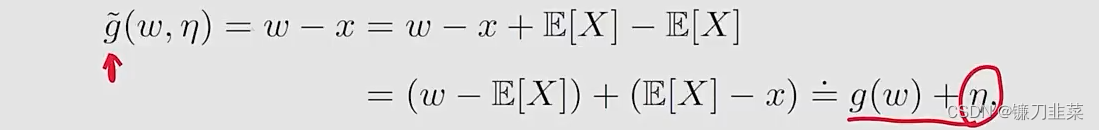
3)求解g(x)=0g(x)=0g(x)=0的RM算法是wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−xk)w_{k+1}=w_k-\alpha_k \tilde{g}(w_k, \eta_k)=w_k-\alpha_k(w_k-x_k)wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−xk),这就是之前给出的mean estimation算法。
Dvoretzkys convergence theorem

- 这是一个比RM定理更一般化的结论,可以用来证明RM定理
- 它可以直接用来分析
mean estimation problem - 它的一个扩展可以用来分析
Q-learning和TD learning算法。
Stochastic gradient descent
stochastic gradient descent(SGD)算法在机器学习和强化学习的许多领域中广泛应用;SGD也是一个特殊的RM算法,而且mean estimation algorithm是一个特殊的SGD算法。
算法描述
假设我们的目标是求解下面优化问题:minwJ(w)=E[f(w,X)]\min_{w} J(w)=\mathbb{E}[f(w, X)]wminJ(w)=E[f(w,X)]
- www是被优化的参数
- XXX是一个随机变量,The expection实际上就是针对这个XXX进行计算的
- www和XXX可以是标量或者向量,函数f(⋅)f(\cdot)f(⋅)是一个标量。
有三种方法求解:
Method 1: gradient descent (GD)
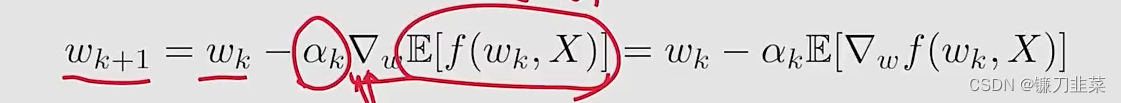
问题是the expected value is difficult to obtain。
Method 2: batch gradient descent (BGD)
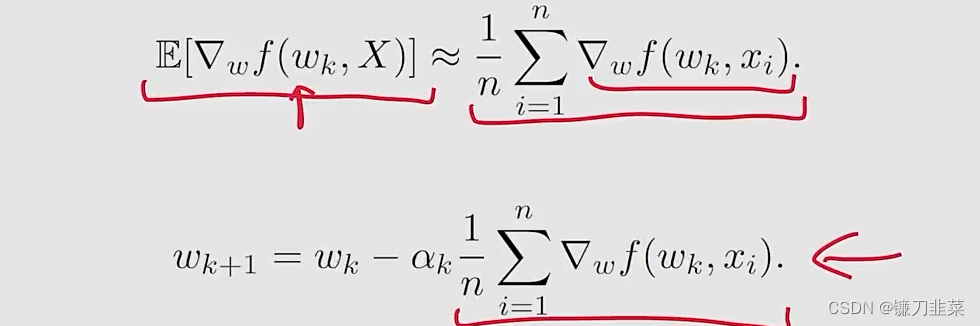
问题是对于每个wkw_kwk,在每次迭代中需要许多次采样。
Method 3: stochastic gradient descent (SGD):

SGD与前面两种算法相比:
- 与gradient descent算法相比,将true gradient E[∇wf(wk,X)]\mathbb{E}[\nabla _w f(w_k, X)]E[∇wf(wk,X)]替换为stochastic gradient ∇wf(wk,xk)\nabla _w f(w_k, x_k)∇wf(wk,xk)
- 与batch gradient descent算法相比,令n=1n=1n=1。
示例和应用
考虑下面的一个优化问题:

其中:

有三个练习:
- 证明最优解是w∗=E[X]w*=\mathbb{E}[X]w∗=E[X]
- 用GD算法求解这个问题
- 用SGD算法求解这个问题
首先看第一个练习:
对J(w)J(w)J(w)求梯度,使其等于0,即可得到最优解,因此有∇wJ(w)=0\nabla _w J(w)=0∇wJ(w)=0,然后根据公式,得到E[∇wf(w,X)]=0\mathbb{E}[\nabla_wf(w,X)]=0E[∇wf(w,X)]=0,然后得到E[w−X]=0\mathbb{E}[w-X]=0E[w−X]=0,由于w是一个常数,因此w=E[X]w=\mathbb{E}[X]w=E[X]。
第二个联系的答案是:
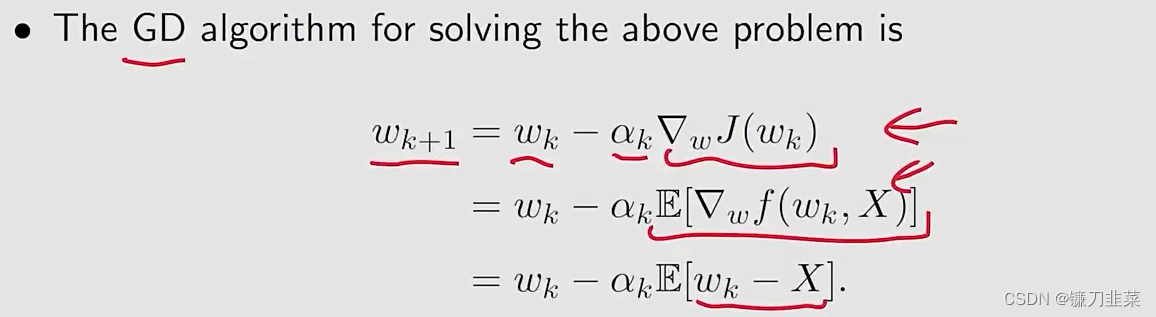
相应的,使用SGD算法求解上面问题:
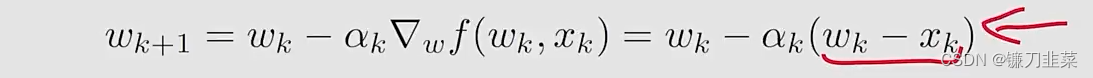
收敛性分析
从GD到SGD:

∇wf(wk,xk)\nabla _w f(w_k, x_k)∇wf(wk,xk)被视为E[∇wf(wk,X)]\mathbb{E}[\nabla _w f(w_k, X)]E[∇wf(wk,X)]的一个noisy measurement:
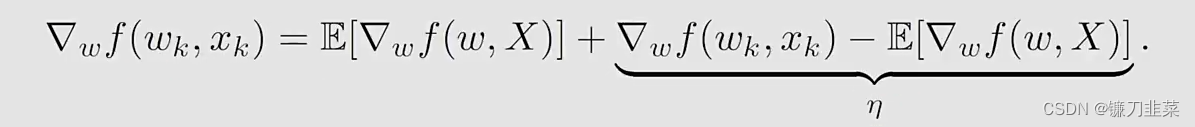
不管怎样,由于∇wf(wk,xk)≠E[∇wf(wk,X)]\nabla _w f(w_k, x_k)\ne \mathbb{E}[\nabla _w f(w_k, X)]∇wf(wk,xk)=E[∇wf(wk,X)],是否基于SGD随着k趋近于无穷,wk→w∗w_k\rightarrow w*wk→w∗?答案是肯定的。
这里的方式证明SGD是一个特殊的RM算法,自然地得到收敛性。SGD的目标是最小化J(w)=E[f(w,X)]J(w)=\mathbb{E}[f(w, X)]J(w)=E[f(w,X)]
这个问题可以转换为一个root-finding问题:∇wJ(W)=E[∇wf(w,X)]=0\nabla_w J(W)=\mathbb{E}[\nabla _w f(w, X)]=0∇wJ(W)=E[∇wf(w,X)]=0
令g(w)=∇wJ(W)=E[∇wf(w,X)]g(w)=\nabla_w J(W)=\mathbb{E}[\nabla _w f(w, X)]g(w)=∇wJ(W)=E[∇wf(w,X)],那么SGD的目标就是找到满足g(w)=0g(w)=0g(w)=0的根。
这里使用RM算法求解,因为g(w)的表达式未知,所以要用到数据。what we can measure is
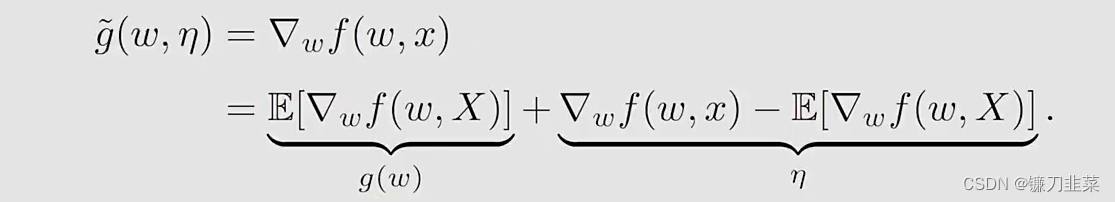
然后,RM算法求解g(w)=0g(w)=0g(w)=0就得到
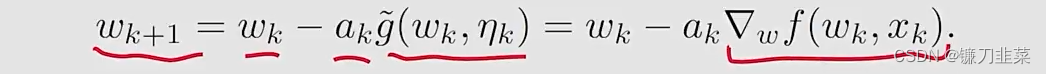
- It is exacely the SGD algorithm
- 因此,SGD是一个特殊的RM算法。
因为SGD算法是一个特殊的RM算法,它的收敛性遵从:

收敛模式
问题:由于stochastic gradient是随机的,那么approximation是不精确的,是否SGD的收敛性是slow或者random?
为了回答这个问题,我们考虑在stochastic和batch gradients之间的一个relative error:
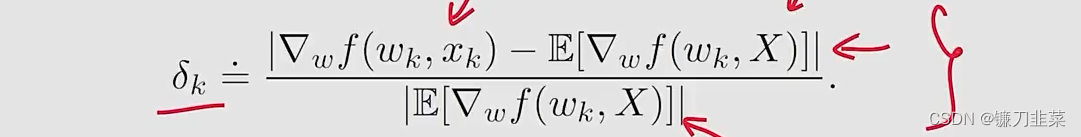
由于E[∇wf(w∗,X)]=0\mathbb{E}[\nabla_w f(w*, X)]=0E[∇wf(w∗,X)]=0,我们有:
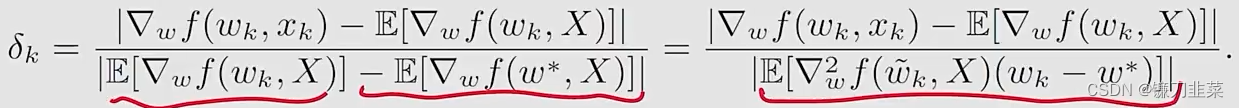
其中后面等式的分母使用了一个mean value theorem(中值定理),并且w~k∈[wk,w∗]\tilde{w}_k\in [w_k, w*]w~k∈[wk,w∗]

假设fff是严格凸的,满足∇w2f≥c>0\nabla_w^2f \ge c > 0∇w2f≥c>0对于所有的w,Xw, Xw,X,其中ccc是一个positive bound。
然后,δk\delta_kδk的证明就变为了
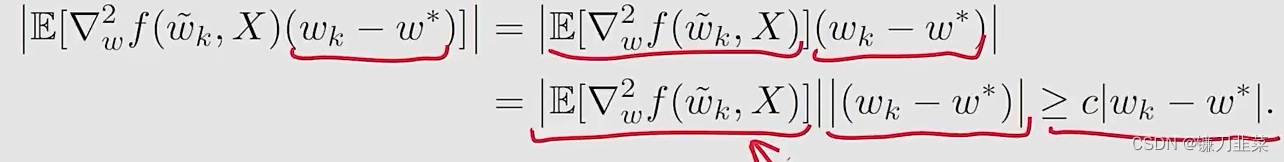
然后把这个分母的性质带入刚才的relative error公式,就得到

再看上面的式子:
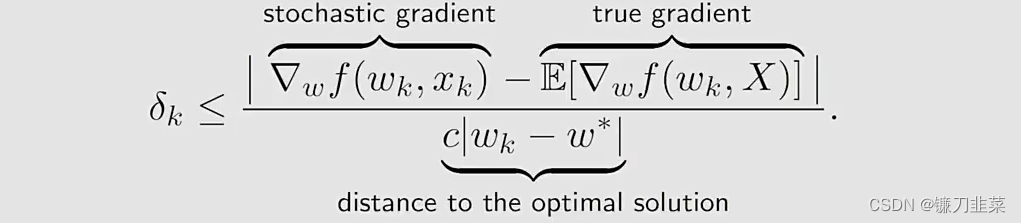
这个公式也表明了SGD的一个有趣的收敛模式:
- relative error δk\delta_kδk与∣wk−w∗∣|w_k-w*|∣wk−w∗∣成反比
- 当∣wk−w∗∣|w_k-w*|∣wk−w∗∣比较大时,δk\delta_kδk较小,SGD的表现与GD相似(behaves like)
- 当wkw_kwk接近w∗w*w∗,相对误差可能较大,收敛性在w∗w*w∗的周边存在较多的随机性。
考虑一个例子:
Setup:

Result:
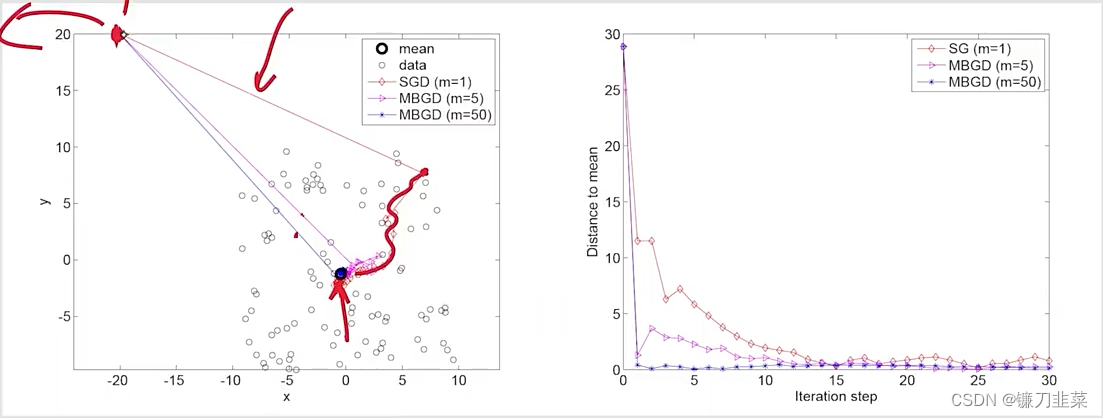
MBGD:mini-batch gradient descent
- 尽管在初始的时候,mean远离true value,但是SGD estimate can approach the neighborhood of the true value fast.
- 当estimate接近true value,它具有一定程度的随机性,但是仍然逐渐靠近the true value
一个确定性公式
在之前介绍的SGD的formulation中,涉及random variable和expectation。但是在学习其他材料的时候可能会遇到一个SGD的deterministic formulation,不涉及任何random variables。
同样地,考虑这样一个优化问题:minwJ(w)=1n∑i=1nf(w,xi)\min_w J(w)=\frac{1}{n}\sum_{i=1}^n f(w, x_i)wminJ(w)=n1i=1∑nf(w,xi)
- f(w,xi)f(w, x_i)f(w,xi)是一个参数化的函数
- www是需要被优化的参数
- 一组实数{xi}i=1n\{x_i\}_{i=1}^n{xi}i=1n,其中xix_ixi不必是任意random variable的一个采样,反正就是一组实数。
求解这个问题的gradient descent算法如下:
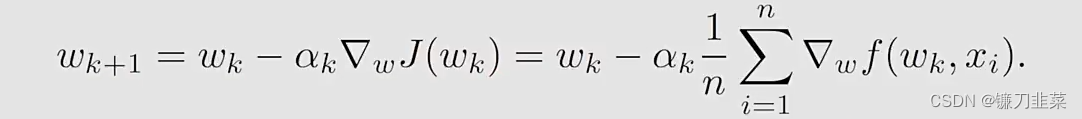
假设这样的一个实数集合比较大,每次只能得到一个xix_ixi,在这种情况下,可以使用下面的迭代算法:wk+1=wk−αk∇wf(wk,xk)w_{k+1}=w_k-\alpha_k \nabla_w f(w_k, x_k)wk+1=wk−αk∇wf(wk,xk)
那么问题来了:
- 这个算法是SGD吗?它没有涉及任何random variable或者expected values.
- 我们该如何定义这样一组实数{xi}i=1n\{x_i\}_{i=1}^n{xi}i=1n? 是应该将它们按照某种顺序一个接一个地取出?还是随机地从这个集合中取出?
回答上面问题的思路是:我们手动地引入一个random variable,并将SGD从deterministic formulation转换为stochastic formulation。
具体地,假设一个XXX是定义在集合{xi}i=1n\{x_i\}_{i=1}^n{xi}i=1n的random variable。假设它的概率分布是均匀的,即p(X=xi)=1/np(X=x_i)=1/np(X=xi)=1/n
然后,这个deterministic optimization problem变成了一个stochastic one:
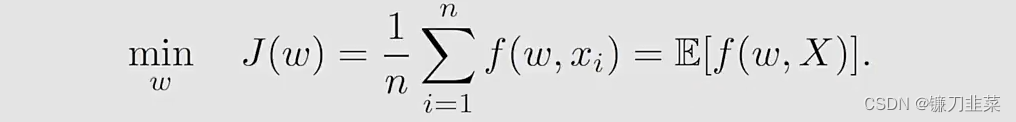
- 上面等式的后面是strict,而不是approximate。因此,这个算法是SGD。
- The estimate converges if xkx_kxk is uniformly and independently sampled from {xi}i=1n\{x_i\}_{i=1}^n{xi}i=1n. xkx_kxk may repreatedly take the same number in {xi}i=1n\{x_i\}_{i=1}^n{xi}i=1n since it is sampled randomly。
BGD, MBGD和SGD
假设我们想要最小化J(w)=E[f(w,X)]J(w)=\mathbb{E}[f(w,X)]J(w)=E[f(w,X)],给定一组来自XXX的随机采样{xi}i=1n\{x_i\}_{i=1}^n{xi}i=1n。分别用BGD,SGD,MBGD求解这个问题:

在BGD算法中:

在MBGD算法中:

在SGD算法中

MBGD与BGD和SGD进行比较:
- 与SGD相比,MBGD具有更少的随机性,因为它使用更多的采样数据,而不是像SGD中那样仅仅使用一个。
- 与BGD相比,MBGD在每次迭代中不要求使用全部的samples,这使其更加灵活和高效
- if m=1, MBGD变为SGD
- if m=n, MBGD does NOT become BGD strictly speaking,因为MBGD使用n个样本的随机采样,而BGD使用所有n个样本。特别地,MBGD可能使用{xi}i=1n\{x_i\}_{i=1}^n{xi}i=1n中的一个值很多次,而BGD使用每个数值一次。
举个例子:给定一些数值{xi}i=1n\{x_i\}_{i=1}^n{xi}i=1n,我们的目标是计算平均值mean: xˉ=∑i=1nxi/n\bar{x}=\sum_{i=1}^n x_i/nxˉ=∑i=1nxi/n。这个问题可以等价成一个优化问题:minwJ(w)=12n∑i=1n∣∣w−wi∣∣2\min_w J(w)=\frac{1}{2n}\sum_{i=1}^n||w-w_i||^2wminJ(w)=2n1i=1∑n∣∣w−wi∣∣2分别用三个算法求解这个优化问题:
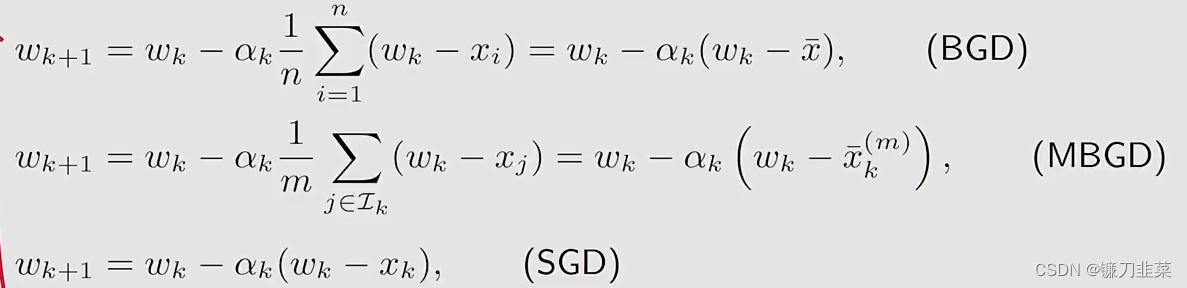
其中xˉk(m)=∑j∈Lkxj/m\bar{x}_k^{(m)}=\sum_{j\in \mathcal{L}_k} x_j/mxˉk(m)=∑j∈Lkxj/m
更进一步地,如果αk=1/k\alpha_k=1/kαk=1/k,上面等式可以求解为:
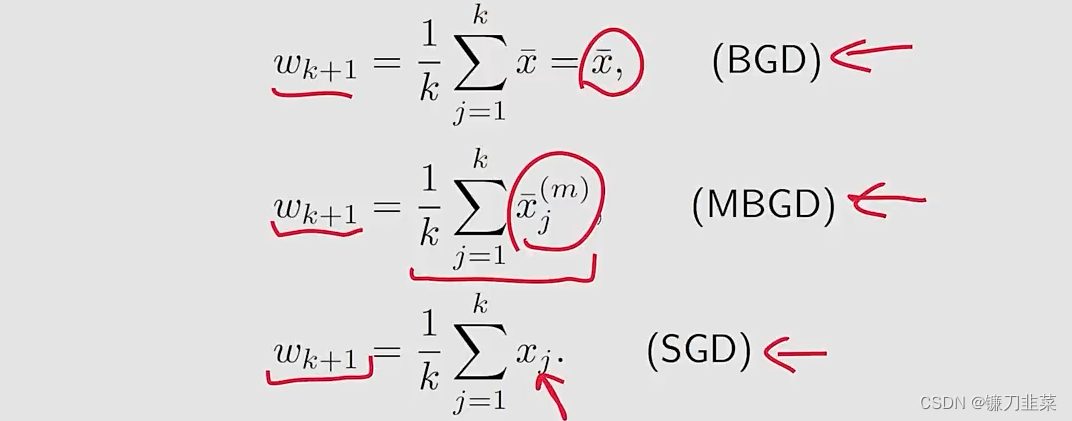
- BGD在每一步的estimate是exactly the optimal solution w∗=xˉw*=\bar{x}w∗=xˉ
- MBGD的estimate比SGD更快靠近mean,因为xˉk(m)\bar{x}_k^{(m)}xˉk(m)已经是一个平均。
仿真结果:令αk=1/k\alpha_k=1/kαk=1/k,给定100个点,使用不同的mini-batch size得到不同的收敛速度:
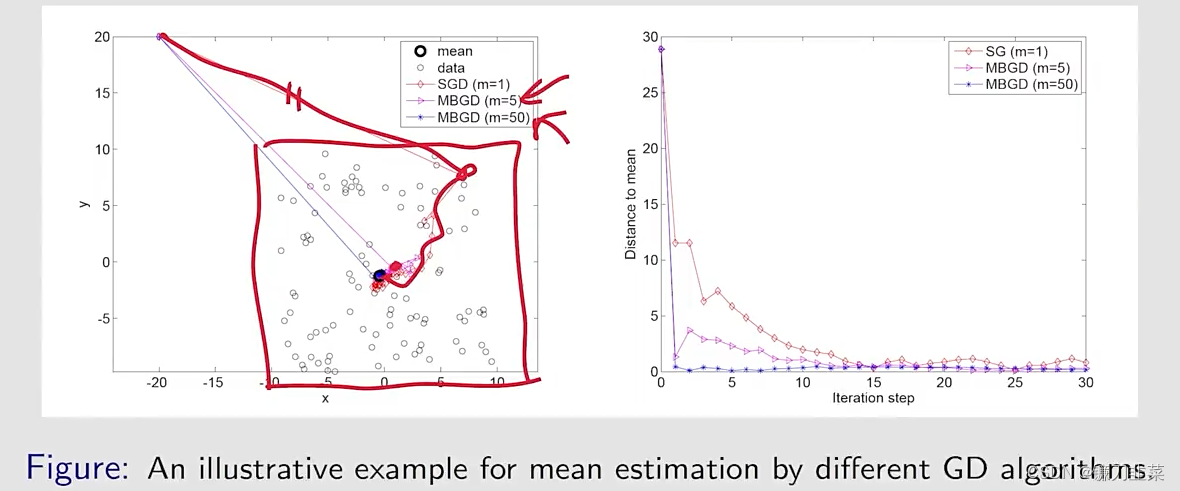
总结
- Mean estimation: 使用{xk}\{x_k\}{xk}计算E[X]\mathbb{E}[X]E[X]:wk+1=wk−1k(wk−xk)w_{k+1}=w_k-\frac{1}{k}(w_k-x_k)wk+1=wk−k1(wk−xk)
- RM算法:使用{g~(wk,ηk)}\{\tilde{g}(w_k,\eta_k)\}{g~(wk,ηk)}求解g(w)=0g(w)=0g(w)=0:wk+1=wk−akg~(wk,ηk)w_{k+1}=w_k-a_k\tilde{g}(w_k,\eta_k)wk+1=wk−akg~(wk,ηk)
- SGD算法:使用{∇wf(wk,xk)}\{\nabla_wf(w_k, x_k)\}{∇wf(wk,xk)}最小化J(w)=E[f(w,X)]J(w)=\mathbb{E}[f(w,X)]J(w)=E[f(w,X)]: wk+1=wk−αk∇wf(wk,xk)w_{k+1}=w_k-\alpha_k \nabla_wf(w_k, x_k)wk+1=wk−αk∇wf(wk,xk)
内容来源
- 《强化学习的数学原理》 西湖大学工学院赵世钰教授 主讲
- 《动手学强化学习》 俞勇 著
相关文章:

【强化学习】强化学习数学基础:随机近似理论与随机梯度下降
强化学习数学基础:随机近似理论与随机梯度下降Stochastic Approximation and Stochastic Gradient Descent举个例子Robbins-Monro algorithm算法描述举个例子收敛性分析将RM算法用于mean estimationStochastic gradient descent算法描述示例和应用收敛性分析收敛模式…...

ThreadLocal 学习常见问题
ThreadLocal 这个此类提供线程局部变量。这些变量不同于通常的对应变量,因为每个访问一个变量的线程(通过 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是希望将状态与线程(例如,用户 ID 或事务 ID)关联的类中的私有静态字段。使…...
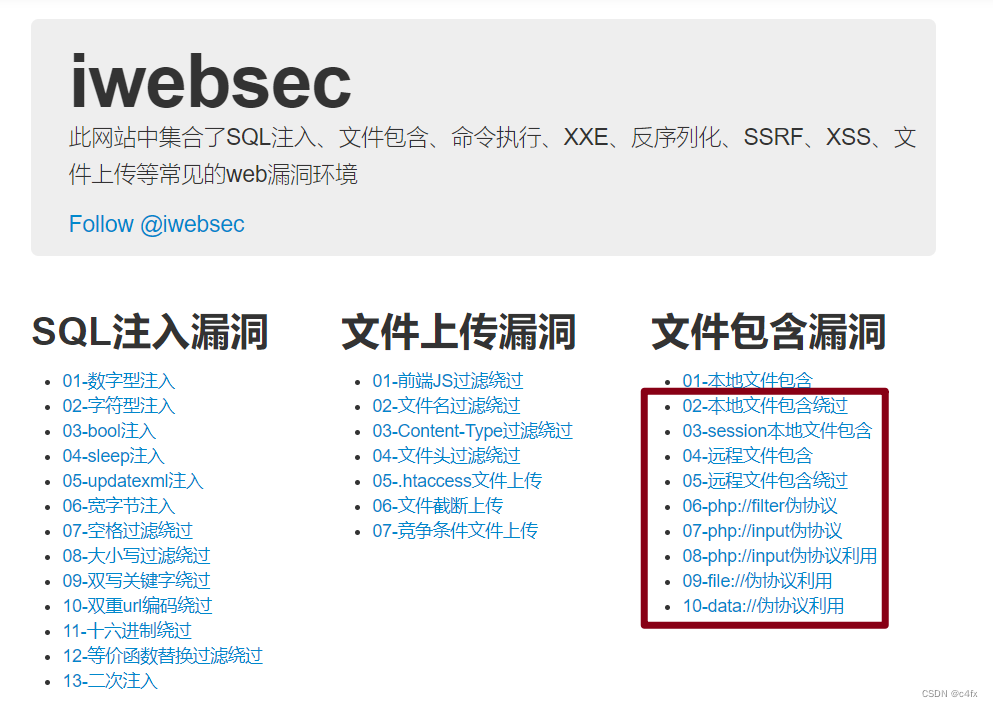
文件包含漏洞1 | iwebsec
文章目录00-文件包含漏洞原理环境01-本地文件包含读取敏感文件信息配合文件上传getshell配合日志文件getshell配合SSH日志配合运行环境00-文件包含漏洞原理 为什么要文件包含? 为什么会有文件包含漏洞? 因为将被包含的文件设置为变量,用来进行动态调用…...

基于MindAR实现的网页端WebAR图片识别叠加动作模型追踪功能(含源码)
前言 由于之前一直在做这个AR/VR 相关的功能开发,大部分的时候实现方式都是基于高通Vuforia或者EasyAR等基于Unity3d的引擎的开发,这样开发的程序大部分都是运行在APP上,安卓或者ios的开发也能一次性搞定。不过当时大部分的需求都是需要在网…...
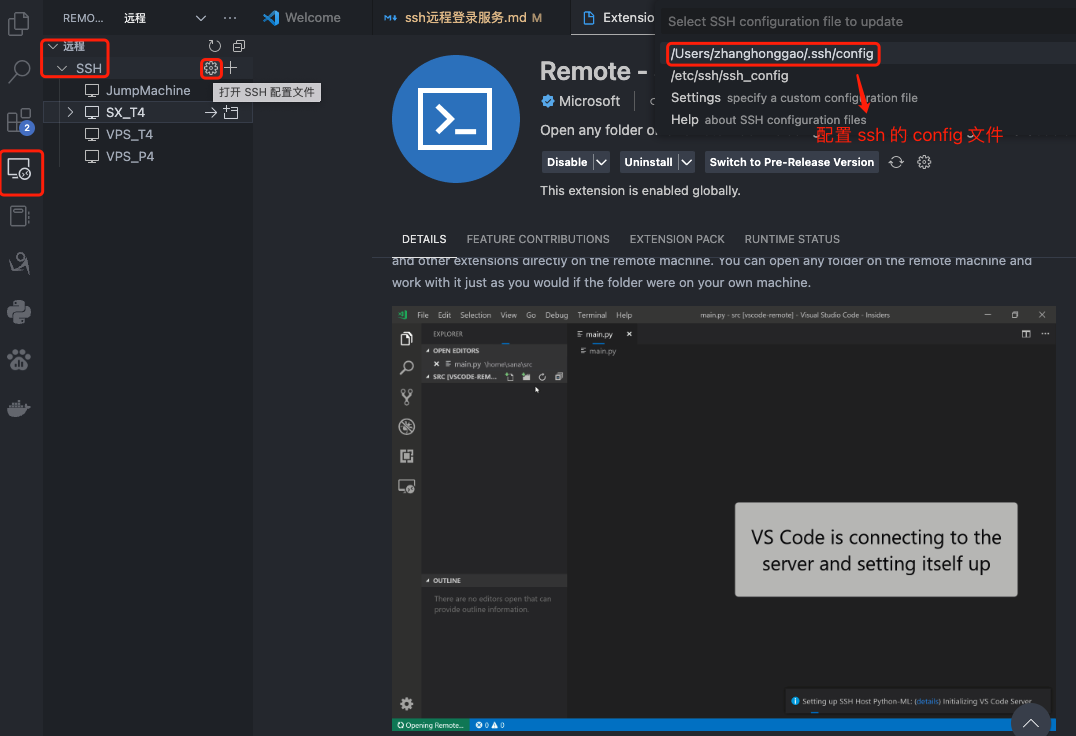
ssh 远程连接方式总结
SSH 概述 SSH(安全外壳协议 Secure Shell Protocol,简称SSH)是一种加密的网络传输协议,用于在网络中实现客户端和服务端的连接,典型的如我们在本地电脑通过 SSH连接远程服务器,从而做开发,Wind…...

springboot+mybatisPlus简单实现数据分页显示
项目地址:https://gitee.com/flowers-bloom-is-the-sea/geo_demo/tree/v1.0/ 这个项目的测试是可以的。 先来查看一些tb_shop表: id name x y ------ ------ ------ --------里面是空数据,那么现在对数据里插入一些数据…...

axios的基本使用
axios 安装axios npm install axios 使用时先导入 import axios from ‘axios’ axios请求方式 axios支持多种请求方式 axios(config) axios.request(config) axios.get(url[, config]) axios.head(url, [, config]) axios.post(url[, data[, config]]) axios.put(url[, dat…...
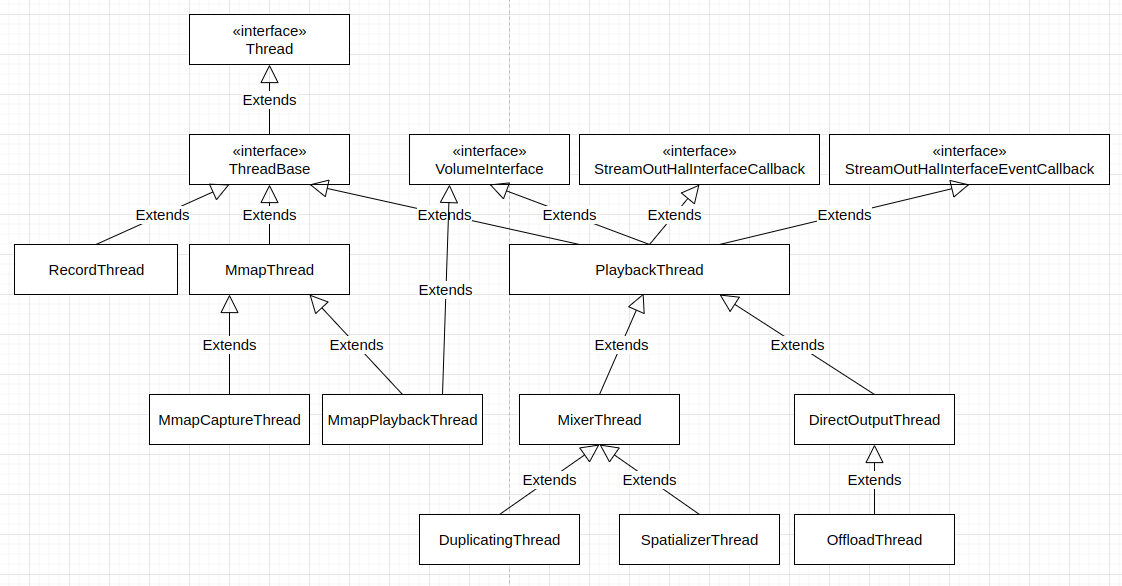
核心 Android 调节音量的过程
核心 Android 系统提供的调节音量的方法 核心 Android 系统提供了多种调节音量的方法,这些方法主要包括如下这些。 如在 Android Automotive 调节音量的过程 中我们看到的,CarAudioService 最终在 CarAudioDeviceInfo 中 (packages/services/Car/servi…...

用C/C++制作一个简单的俄罗斯方块小游戏
用C/C制作一个简单的俄罗斯方块小游戏 用C/C制作一个简单的俄罗斯方块小游戏 0 准备1 游戏界面设计 1.1 界面布局1.2 用 EasyX 显示界面1.3 音乐播放 2 方块设计 2.1 方块显示2.2 随机生成一个方块2.3 方块记录 3 方块移动和旋转 3.1 方块的移动3.2 方块的旋转3.3 方块的碰撞和…...
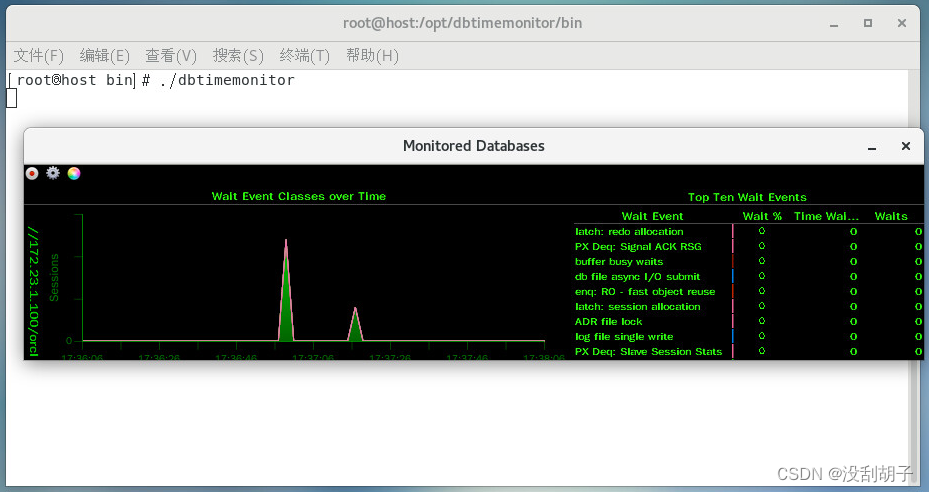
使用免费负载生成器swingbench对oracle数据库进行压力测试(测试Oracle的功能或评估性能)
1.Swingbench 简介 Swingbench 是一个免费负载生成器(和基准测试),旨在对 Oracle 数据库 进行压力测试。目前最新版本 Swingbench 2.6。 SwingBench 由负载生成器,协调器和集群概述组成。该软件可以生成负载 并绘制交易/响应时间…...
【预告】ORACLE Primavera P6 v22.12 虚拟机发布
引言 离ORACLE Primavera P6 EPPM最新系统 v22.12已过去了3个多月,应盆友需要,也为方便大家体验,我近日将构建最新的P6的虚拟环境,届时将分享给大家,最终可通过VMWare vsphere (esxi) / workstation 或Oracle virtua…...

机器学习100天(四十):040 线性支持向量机-公式推导
《机器学习100天》完整目录:目录 机器学习 100 天,今天讲的是:线性支持向量机-公式推导! 首先来看这样一个问题,在二维平面上需要找到一条直线划分正类和负类。 我们找到了 A、B、C 三条直线。这三条直线都能正确分类所有训练样本。但是,哪条直线最好呢?直观上来看,我…...

失败经验之震荡玩家往往死于趋势市场
亏损,是从去年开始的吧。 尤其是去年,仅仅一年,就亏掉了自从交易以来的所有盈利。 现在,我甚至不敢去计算具体的亏损金额。 保守估计,已经亏损100万左右。 现在回想,似乎也是必然。 交易本来就是一个走…...
应用层与传输层~
文章目录应用层自定义应用层协议什么是自定义应用层协议自定义方式运输层运输层概述运输层特点运输层协议UDP协议UDP的特点UDP首部格式校验规则TCP协议TCP的特点TCP协议段格式TCP的性质确认序号超时重传连接管理三次握手四次挥手TCP的状态滑动窗口流量控制拥塞控制延迟应答捎带…...
IO文件操作
认识文件 狭义的文件 存储在硬盘上的数据,以“文件"为单位,进行组织 常见的就是普通的文件 (文本文件,图片, office系列,视频,音频可执行程序…)文件夹也叫做"目录" 也是一种特殊的文件。 广义的文件 操作系统,是要负责管理软硬件资源,操作系统(…...

【构建工具】webpack 3、4 升级指南,摆脱低版本的困扰
一、依赖处理 1.升级通用依赖 借用 ncu 库实现,帮你改写需要升级的package.json 然后再 npm install ncu -u <packages> # 可以指定依赖 ncu # 升级全部依赖大概列了下升级的效果 add-asset-html-webpack-plugin ^2.1.3 → ^5.0.2 clean-webpack-…...

Javaweb第一个项目——实现简单的登陆功能
第一步:打开idea-->文件-->新建 第二步: 在Demo文件夹 点击右键-->添加框架支持-->找到Web应用程序 勾选 第三步:配置Tomcat 第四步:新建一个lib(建在web-INF文件夹下)文件夹 用于存放jar包…...

OpenKruise 开发者不容错过的带薪实习机会!马上加入 LFX Mentorship 计划
LFX Mentorship 计划由 Linux Foundation 组织发起,为像 OpenKruise 这样的 CNCF 托管项目提供了激励开源贡献、扶植社区发展的优秀土壤。参与其中的开发者不仅有机会在经验丰富的社区 Mentor 指导下贡献开源项目、为职业生涯加分,完成工作后还能获得 $3…...

《c++ primer笔记》第八章 IO库
前言 简单看一下就行 文章目录一、IO类1.1基本概念1.2管理输出缓冲二、文件输入输出2.1文件模式三、string流3.1istringstream3.2ostringstream一、IO类 1.1基本概念 我们常见的流有istream和ostream,这两个流都是有关输入和输出的,此外,…...
web开发 用idea创建一个新项目
这个写着就是给自己当备忘录用的QAQ 这个老师上课一通操作啥也没看清…卑微搞了半天看样子是成功了 记录一下省的以后忘了怎么创建(? zufe lxy 2023.3 先行条件是已经自己装好了Tomcat和idea!!(我的idea是申请了教育…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
