【LLM】LLama2模型(RMSNorm、SwiGLU、RoPE位置编码)
note
- 预训练语言模型除了自回归(Autoregressive)模型GPT,还有自编码模型(Autoencoding)BERT[1]、编-解码(Encoder-Decoder)模型BART[67],以及融合上述三种方法的自回归填空(Autoregressive Blank Infilling)模型GLM(General Language Model)[68]。
- ChatGPT的出现,使得目前几乎所有大语言模型神经网络结构趋同,采用自回归模型,基础架构与GPT-2相同,但在归一化函数、激活函数及位置编码等细节方面有所不同。归一化函数和激活函数的选择对于大语言模型的收敛性具有一定影响,因此在LLaMA 模型被提出之后,大多数开源模型沿用了RMSNorm 和SwiGLU 的组合方式。
- 由于LLaMA 模型所采用的位置编码方法RoPE 的外推能力不好,因此后续一些研究采用了ALiBi[69] 等具有更好外推能力的位置编码方法,使模型具有更长的上下文建模能力。
- 很多博客推导公式rope很复杂,用到了矩阵运算、复数运算、欧拉公式、三角展开式,整体过程很繁琐。如果我们直接利用旋转矩阵的性质,推导会很简洁。假设Ra表示角度为a的旋转矩阵,那么R具有如下性质:
-
- Ra^T = R(-a)
-
- Ra Rb = R(a+b)
- 回到旋转位置编码,我们可以去证明 <RaX, RbY> = <X, R(b-a)Y> ,证明如下:
<RaX, RbY>
= (RaX)^T RbY
= X^T Ra^T RbY
= X^T R(b-a) Y
= <X, R(b-a)Y>
-
Llama 2 模型
论文:《Llama 2: Open Foundation and Fine-Tuned Chat Models》
链接:https://arxiv.org/pdf/2307.09288.pdf

亮点:llama2是市面上为数不多的经过RLHF对齐训练后的大模型,记录的如从最开始的有监督微调(SFT-v1) 到最终使用 PPO + RLHF 微调(RLHF-v5) 的演变历程。
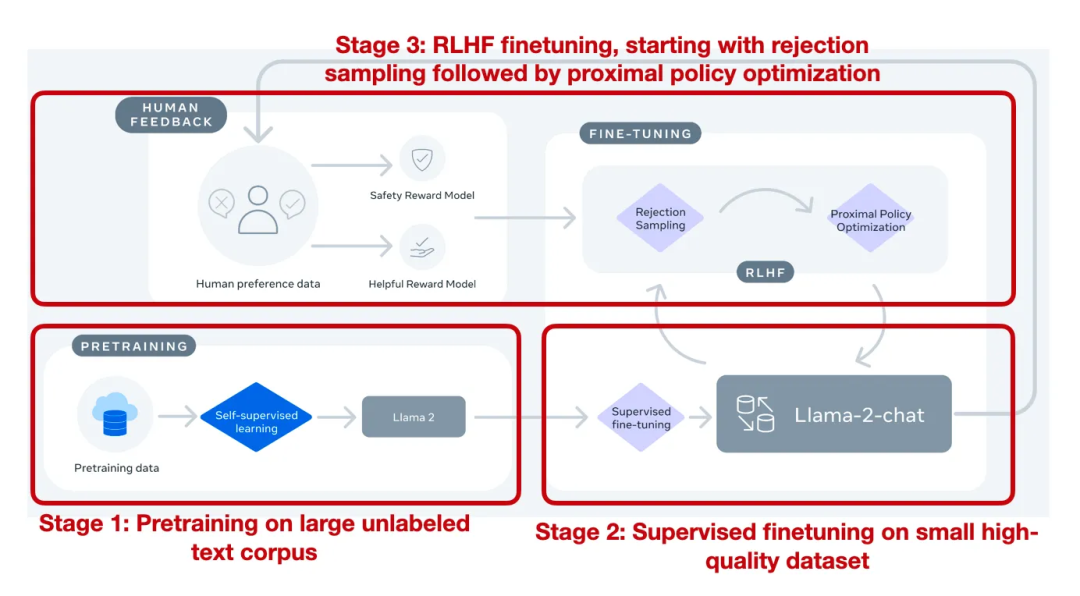
模型结构
和很多LLM类似也是使用自回归的方式构建语言模型,但在位置编码、层归一化位置、激活函数等细节不同。模型结构和GPT2类似:

主要的不同点:
- 前置的RMSNorm层
- Q在与K相乘之前,先使用RoPE进行位置编码
- K V Cache,并采用Group Query Attention
- FeedForward层
不同规模的llama模型使用的超参数也有所不同:

RMSNorm归一化函数
回顾LN层(对同一个样本的不同特征进行归一化)归一化的公式:
LayerNorm : y = x − E [ x ] Var [ x ] + ϵ ∗ γ + β E [ x ] = 1 N ∑ i = 1 N x i Var [ x ] = 1 N ∑ i = 1 N ( x i − E [ x ] ) 2 \begin{aligned} \text { LayerNorm }: y & =\frac{x-E[x]}{\sqrt{\operatorname{Var}[x]+\epsilon}} * \gamma+\beta \\ E[x] & =\frac{1}{N} \sum_{i=1}^N x_i \\ \operatorname{Var}[x] & =\frac{1}{N} \sum_{i=1}^N\left(x_i-E[x]\right)^2 \end{aligned} LayerNorm :yE[x]Var[x]=Var[x]+ϵx−E[x]∗γ+β=N1i=1∑Nxi=N1i=1∑N(xi−E[x])2
而RMSNorm就是LayerNorm的变体, RMSNorm省去了求均值的过程,也没有了偏置 β \beta β,(如下),RMSNorm使用均方根进行归一化
RMSNorm : y = x Mean ( x 2 ) + ϵ ∗ γ Mean ( x 2 ) = 1 N ∑ i = 1 N x i 2 \begin{aligned} \text { RMSNorm }: y & =\frac{x}{\sqrt{\operatorname{Mean}\left(x^2\right)+\epsilon}} * \gamma \\ \operatorname{Mean}\left(x^2\right) & =\frac{1}{N} \sum_{i=1}^N x_i^2 \end{aligned} RMSNorm :yMean(x2)=Mean(x2)+ϵx∗γ=N1i=1∑Nxi2
其中 γ \gamma γ 和 β \beta β 为可学习的参数。
RMSNorm的优点:
【换种形式】针对输入向量a,RMSNorm 函数计算公式如下: RMS ( a ) = 1 n ∑ i = 1 n a i 2 a ˉ i = a i RMS ( a ) \begin{aligned} \operatorname{RMS}(\boldsymbol{a}) & =\sqrt{\frac{1}{n} \sum_{i=1}^n \boldsymbol{a}_i^2} \\ \bar{a}_i & =\frac{a_i}{\operatorname{RMS}(\boldsymbol{a})} \end{aligned} RMS(a)aˉi=n1i=1∑nai2=RMS(a)ai
此外,RMSNorm 还可以引入可学习的缩放因子 g i g_i gi 和偏移参数 b i b_i bi ,从而得到 a ˉ i = a i RMS ( a ) g i + b i \bar{a}_i=\frac{a_i}{\operatorname{RMS}(\boldsymbol{a})} g_i+b_i aˉi=RMS(a)aigi+bi
# hidden_size是隐藏层大小,比如每个样本有5个特征,则hidden_size=5
class LlamaRMSNorm(nn.Module):def __init__(self, hidden_size, eps=1e-6):"""LlamaRMSNorm is equivalent to T5LayerNorm"""super().__init__()self.weight = nn.Parameter(torch.ones(hidden_size)) # 以hidden_size大小的全1张量初始化self.variance_epsilon = eps # 给定一个很小的数,防止分母为0def forward(self, hidden_states):input_dtype = hidden_states.dtypehidden_states = hidden_states.to(torch.float32)variance = hidden_states.pow(2).mean(-1, keepdim=True)hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)return self.weight * hidden_states.to(input_dtype) # to(input_dtype)是为了保持数据类型
SwiGLU 激活函数
SwiGLU 激活函数是Shazeer 在文献[50] 中提出的,在PaLM[14] 等模型中进行了广泛应用,并且取得了不错的效果,相较于ReLU 函数在大部分评测中都有不少提升。
在LLaMA 中,全连接层使用带有SwiGLU 激活函数的FFN (Position-wise Feed-Forward Network,FFN通常由两个线性变化组成,这里中间应用SwiGLU非线性激活函数) 的计算公式如下:
FFN SwiGLU ( x , W , V , W 2 ) = SwiGLU ( x , W , V ) W 2 SwiGLU ( x , W , V ) = Swish β ( x W ) ⊗ x V Swish β ( x ) = x σ ( β x ) \begin{array}{r} \operatorname{FFN}_{\text {SwiGLU }}\left(\boldsymbol{x}, \boldsymbol{W}, \boldsymbol{V}, \boldsymbol{W}_2\right)=\operatorname{SwiGLU}(\boldsymbol{x}, \boldsymbol{W}, \boldsymbol{V}) \boldsymbol{W}_2 \\ \operatorname{SwiGLU}(\boldsymbol{x}, \boldsymbol{W}, \boldsymbol{V})=\operatorname{Swish}_\beta(\boldsymbol{x} \boldsymbol{W}) \otimes \boldsymbol{x} \boldsymbol{V} \\ \operatorname{Swish}_\beta(\boldsymbol{x})=\boldsymbol{x} \sigma(\boldsymbol{\beta} \boldsymbol{x}) \end{array} FFNSwiGLU (x,W,V,W2)=SwiGLU(x,W,V)W2SwiGLU(x,W,V)=Swishβ(xW)⊗xVSwishβ(x)=xσ(βx)
其中 σ ( x ) \sigma(x) σ(x) 是Sigmoid 函数
下图给出了Swish 激活函数在参数 β \beta β 不同取值下的形状。可以看到:
- 当 β \beta β 趋近于 0 时,Swish 函数趋近于线性函数 y = x y=x y=x;
- 当 β \beta β 趋近于无穷大时,Swish 函数趋近于 ReLU 函数;
- 当 β \beta β 取值为 1 时,Swish 函数是光滑且非单调的。
在HugqingFace 的 transformer库中Swish 函数被SiLU 函数代替。
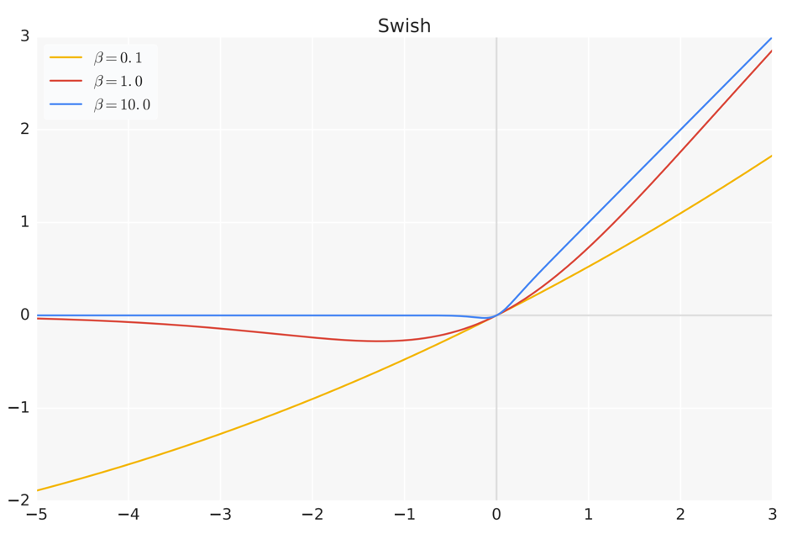
使用SwiGLU的目的在于提供一种更有效的激活方式,它可以帮助模型更好地学习数据中的复杂模式和关系。Swish激活函数因其平滑性和非零的梯度对于负值的处理,已被证明在多种任务中优于传统的ReLU函数。将Swish与GLU结合,SwiGLU通过门控机制进一步增强了模型的选择性信息传递能力,这有助于提高模型在特定任务,如自然语言处理和图像识别中的表现。
我们来看具体代码,比较不同激活函数(实际用的时候可以直接使用torch的F.silu函数,SiLU其实就是beta为1时的Swish激活函数):
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import normdef gelu(x):return x * norm.cdf(x)def relu(x):return np.maximum(0, x)def swish(x, beta=1):return x * (1 / (1 + np.exp(-beta * x)))x_values = np.linspace(-5, 5, 500)
gelu_values = gelu(x_values)
relu_values = relu(x_values)
swish_values = swish(x_values)
swish_values2 = swish(x_values, beta=0.5)plt.plot(x_values, gelu_values, label='GELU')
plt.plot(x_values, relu_values, label='ReLU')
plt.plot(x_values, swish_values, label='Swish')
plt.plot(x_values, swish_values2, label='Swish (beta=0.5)')
plt.title("GELU, ReLU, and Swish Activation Functions")
plt.xlabel("x")
plt.ylabel("Activation")
plt.grid()
plt.legend()
save_path = "xxx"
plt.savefig(save_path)
plt.show()

RoPE位置嵌入
(1)数学基础知识回顾
旋转矩阵是正交矩阵的一种特例, 它们在数学和物理学中都有广泛的应用。下面是关于正交矩阵和旋转矩阵的一些核心特点的概述:
正交矩阵的定义和特点
- 定义:正交矩阵是方块矩阵, 其元素为实数, 并且其行向量和列向量均为正交的单位向量。这意味着正交矩阵满足 Q T Q = Q Q T = I Q^T Q=Q Q^T=I QTQ=QQT=I, 其中 I I I 是单位矩阵, Q T Q^T QT 是 Q Q Q 的转置矩阵 。
- 行列式值:正交矩阵的行列式值必须为 +1 或 -1 , 这反映了其保持向量空间体积不变的性质
- 性质:
- 作为线性映射, 正交矩阵保持距离不变, 是保距映射。
- 行列式值为 +1 的正交矩阵称为特殊正交矩阵, 代表纯旋转。
- 行列式值为 -1 的正交矩阵代表旋转加上镜像, 即瑕旋转 。
旋转矩阵
- 旋转矩阵:特殊正交矩阵, 其行列式值为 +1 , 专门用于表示空间中的旋转操作。旋转矩阵通过保持向量长度和夹角不变的同时实现空间的旋转变换。
- 应用:旋转矩阵和正交矩阵在多个领域都有广泛的应用, 比如描述分子的点群对称性、数值线性代数中的QR分解、以及在计算机图形学中处理图形旋转等 。
示例
一些小的正交矩阵的例子可能包括:
- 单位矩阵 I I I, 表示恒等变换。
- 特定角度的旋转矩阵, 比如旋转 16.2 6 ∘ 16.26^{\circ} 16.26∘ 的矩阵。
- 针对某一轴的反射矩阵。
- 置换坐标轴的矩阵等 。
(2)rope旋转位置编码
核心:通过绝对位置编码的方式实现相对位置编码
在位置编码上,使用旋转位置嵌入[52] 代替原有的绝对位置编码。RoPE 借助复数的思想,出发点是通过绝对位置编码的方式实现相对位置编码。其目标是通过下述运算给 q , k q, k q,k 添加绝对位置信息:
q ~ m = f ( q , m ) , k ~ n = f ( k , n ) \tilde{\boldsymbol{q}}_m=f(\boldsymbol{q}, m), \tilde{\boldsymbol{k}}_n=f(\boldsymbol{k}, n) q~m=f(q,m),k~n=f(k,n)
经过上述操作, q ~ m \tilde{\boldsymbol{q}}_m q~m 和 k ~ n \tilde{\boldsymbol{k}}_n k~n 就带有了位置 m \mathrm{m} m 和 n \mathrm{n} n 的绝对位置信息。
详细的证明和求解过程可参考论文,最终可以得到二维情况下用复数表示的 RoPE:
f ( q , m ) = R f ( q , m ) e i Θ f ( q , m ) = ∥ q ∥ e i ( Θ ( q ) + m θ ) = q e i m θ f(\boldsymbol{q}, m)=R_f(\boldsymbol{q}, m) e^{i \Theta_f(\boldsymbol{q}, m)}=\|\boldsymbol{q}\| e^{i(\Theta(\boldsymbol{q})+m \theta)}=\boldsymbol{q} e^{i m \theta} f(q,m)=Rf(q,m)eiΘf(q,m)=∥q∥ei(Θ(q)+mθ)=qeimθ
根据复数乘法的几何意义,上述变换实际上是对应向量旋转,所以位置向量称为 “旋转式位置编码" 。还可以使用矩阵形式表示:
f ( q , m ) = ( cos m θ − sin m θ sin m θ cos m θ ) ( q 0 q 1 ) f(\boldsymbol{q}, m)=\left(\begin{array}{cc} \cos m \theta & -\sin m \theta \\ \sin m \theta & \cos m \theta \end{array}\right)\left(\begin{array}{l} \boldsymbol{q}_0 \\ \boldsymbol{q}_1 \end{array}\right) f(q,m)=(cosmθsinmθ−sinmθcosmθ)(q0q1)

根据内积满足线性叠加的性质,任意偶数维的RoPE 都可以表示为二维情形的拼接,即:
f ( q , m ) = ( cos m θ 0 − sin m θ 0 0 0 ⋯ 0 0 sin m θ 0 cos m θ 0 0 0 ⋯ 0 0 0 0 cos m θ 1 − sin m θ 1 ⋯ 0 0 0 0 sin m θ 1 cos m θ 1 ⋯ 0 0 ⋯ ⋯ ⋯ ⋯ ⋱ ⋯ ⋯ 0 0 0 0 ⋯ cos m θ d / 2 − 1 − sin m θ d / 2 − 1 0 0 0 0 ⋯ sin m θ d / 2 − 1 cos m θ d / 2 − 1 ) ⏟ R d ( q 0 q 1 q 2 q 3 ⋯ q d − 2 q d − 1 ) f(\boldsymbol{q}, m)=\underbrace{\left(\begin{array}{ccccccc} \cos m \theta_0 & -\sin m \theta_0 & 0 & 0 & \cdots & 0 & 0 \\ \sin m \theta_0 & \cos m \theta_0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m \theta_1 & -\sin m \theta_1 & \cdots & 0 & 0 \\ 0 & 0 & \sin m \theta_1 & \cos m \theta_1 & \cdots & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \ddots & \cdots & \cdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m \theta_{d / 2-1} & -\sin m \theta_{d / 2-1} \\ 0 & 0 & 0 & 0 & \cdots & \sin m \theta_{d / 2-1} & \cos m \theta_{d / 2-1} \end{array}\right)}_{\boldsymbol{R}_d}\left(\begin{array}{c} \boldsymbol{q}_0 \\ \boldsymbol{q}_1 \\ \boldsymbol{q}_2 \\ \boldsymbol{q}_3 \\ \cdots \\ \boldsymbol{q}_{d-2} \\ \boldsymbol{q}_{d-1} \end{array}\right) f(q,m)=Rd cosmθ0sinmθ000⋯00−sinmθ0cosmθ000⋯0000cosmθ1sinmθ1⋯0000−sinmθ1cosmθ1⋯00⋯⋯⋯⋯⋱⋯⋯0000⋯cosmθd/2−1sinmθd/2−10000⋯−sinmθd/2−1cosmθd/2−1 q0q1q2q3⋯qd−2qd−1
由于上述矩阵 R d R_d Rd 具有稀疏性,因此可以使用逐位相乘 ⊗ \otimes ⊗ 操作进一步提高计算速度。
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):# 计算词向量元素两两分组以后,每组元素对应的旋转角度 # arange生成[0,2,4...126]freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))# t = [0,....end]t = torch.arange(end, device=freqs.device) # type: ignore# t为列向量 freqs为行向量做外积# freqs.shape = (t.len(),freqs.len()) #shape (end,dim//2)freqs = torch.outer(t, freqs).float() # type: ignore# 生成复数# torch.polar(abs,angle) -> abs*cos(angle) + abs*sin(angle)*jfreqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64# freqs_cis.shape = (end,dim//2)return freqs_cis
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):# ndim为x的维度数 ,此时应该为4ndim = x.ndimassert 0 <= 1 < ndimassert freqs_cis.shape == (x.shape[1], x.shape[-1])shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]# (1,x.shape[1],1,x.shape[-1])return freqs_cis.view(*shape)
def apply_rotary_emb(xq: torch.Tensor,xk: torch.Tensor,freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:# xq.shape = [bsz, seqlen, self.n_local_heads, self.head_dim]# xq_.shape = [bsz, seqlen, self.n_local_heads, self.head_dim//2 , 2]# torch.view_as_complex用于将二维向量转换为复数域 torch.view_as_complex即([x,y]) -> (x+yj)# 所以经过view_as_complex变换后xq_.shape = [bsz, seqlen, self.n_local_heads, self.head_dim//2]xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))freqs_cis = reshape_for_broadcast(freqs_cis, xq_) # freqs_cis.shape = (1,x.shape[1],1,x.shape[-1])# xq_ 与freqs_cis广播哈达玛积# [bsz, seqlen, self.n_local_heads, self.head_dim//2] * [1,seqlen,1,self.head_dim//2]# torch.view_as_real用于将复数再转换回实数向量, 再经过flatten展平第4个维度 # [bsz, seqlen, self.n_local_heads, self.head_dim//2] ->[bsz, seqlen, self.n_local_heads, self.head_dim//2,2 ] ->[bsz, seqlen, self.n_local_heads, self.head_dim]xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)return xq_out.type_as(xq), xk_out.type_as(xk)# 精简版Attention
class Attention(nn.Module):def __init__(self, args: ModelArgs):super().__init__()self.wq = Linear(...)self.wk = Linear(...)self.wv = Linear(...)self.freqs_cis = precompute_freqs_cis(dim, max_seq_len * 2)
def forward(self, x: torch.Tensor):bsz, seqlen, _ = x.shapexq, xk, xv = self.wq(x), self.wk(x), self.wv(x)xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)# attention 操作之前,应用旋转位置编码xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)#...# 进行后续Attention计算scores = torch.matmul(xq, xk.transpose(1, 2)) / math.sqrt(dim)scores = F.softmax(scores.float(), dim=-1)output = torch.matmul(scores, xv) # (batch_size, seq_len, dim)# ......
注意力机制
Q在与K相乘之前,先使用RoPE进行位置编码:
class Attention(nn.Module):def __init__(self, args: ModelArgs):super().__init__()self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_headsmodel_parallel_size = fs_init.get_model_parallel_world_size()self.n_local_heads = args.n_heads // model_parallel_sizeself.n_local_kv_heads = self.n_kv_heads // model_parallel_sizeself.n_rep = self.n_local_heads // self.n_local_kv_headsself.head_dim = args.dim // args.n_headsself.wq = ColumnParallelLinear(args.dim,args.n_heads * self.head_dim,bias=False,gather_output=False,init_method=lambda x: x,)self.wk = ColumnParallelLinear(args.dim,self.n_kv_heads * self.head_dim,bias=False,gather_output=False,init_method=lambda x: x,)self.wv = ColumnParallelLinear(args.dim,self.n_kv_heads * self.head_dim,bias=False,gather_output=False,init_method=lambda x: x,)self.wo = RowParallelLinear(args.n_heads * self.head_dim,args.dim,bias=False,input_is_parallel=True,init_method=lambda x: x,)self.cache_k = torch.zeros((args.max_batch_size,args.max_seq_len,self.n_local_kv_heads,self.head_dim,)).cuda()self.cache_v = torch.zeros((args.max_batch_size,args.max_seq_len,self.n_local_kv_heads,self.head_dim,)).cuda()def forward(self,x: torch.Tensor,start_pos: int,freqs_cis: torch.Tensor,mask: Optional[torch.Tensor],):bsz, seqlen, _ = x.shapexq, xk, xv = self.wq(x), self.wk(x), self.wv(x)xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)self.cache_k = self.cache_k.to(xq)self.cache_v = self.cache_v.to(xq)self.cache_k[:bsz, start_pos : start_pos + seqlen] = xkself.cache_v[:bsz, start_pos : start_pos + seqlen] = xvkeys = self.cache_k[:bsz, : start_pos + seqlen]values = self.cache_v[:bsz, : start_pos + seqlen]# repeat k/v heads if n_kv_heads < n_headskeys = repeat_kv(keys, self.n_rep) # (bs, seqlen, n_local_heads, head_dim)values = repeat_kv(values, self.n_rep) # (bs, seqlen, n_local_heads, head_dim)xq = xq.transpose(1, 2) # (bs, n_local_heads, seqlen, head_dim)keys = keys.transpose(1, 2)values = values.transpose(1, 2)scores = torch.matmul(xq, keys.transpose(2, 3)) / math.sqrt(self.head_dim)if mask is not None:scores = scores + mask # (bs, n_local_heads, seqlen, cache_len + seqlen)scores = F.softmax(scores.float(), dim=-1).type_as(xq)output = torch.matmul(scores, values) # (bs, n_local_heads, seqlen, head_dim)output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)return self.wo(output)
Reference
[1] 大模型系列:SwiGLU激活函数与GLU门控线性单元原理解析
[2]《GLU Variants Improve Transformer》
[3] 《Swish: a Self-Gated Activation Function》
[4] 大模型基础|激活函数|从ReLU 到SwiGLU
[5] https://github.com/meta-llama/llama/tree/main/llama
[6] LLaMA 中的旋转式位置编码(Rotary Position Embedding)
[7] Llama 2详解
[8] 逐行对比LLaMA2和LLaMA模型源代码
相关文章:

【LLM】LLama2模型(RMSNorm、SwiGLU、RoPE位置编码)
note 预训练语言模型除了自回归(Autoregressive)模型GPT,还有自编码模型(Autoencoding)BERT[1]、编-解码(Encoder-Decoder)模型BART[67],以及融合上述三种方法的自回归填空…...

【力扣白嫖日记】1934.确认率
前言 练习sql语句,所有题目来自于力扣(https://leetcode.cn/problemset/database/)的免费数据库练习题。 今日题目: 1934.确认率 表:Signups 列名类型user_idinttime_stampdatetime User_id是该表的主键。每一行都…...

TinTin Web3 动态精选:以太坊坎昆升级利好 Layer2,比特币减半进入倒计时
TinTin 快讯由 TinTinLand 开发者技术社区打造,旨在为开发者提供最新的 Web3 新闻、市场时讯和技术更新。TinTin 快讯将以周为单位, 汇集当周内的行业热点并以快讯的形式排列成文。掌握一手的技术资讯和市场动态,将有助于 TinTinLand 社区的开…...

PCL 高斯投影反算:高斯投影坐标转大地坐标(C++详细过程版)
目录 一、算法原理二、代码实现三、结果展示四、测试数据PCL 高斯投影反算:高斯投影坐标转大地坐标(C++详细过程版)由CSDN点云侠原创。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理...
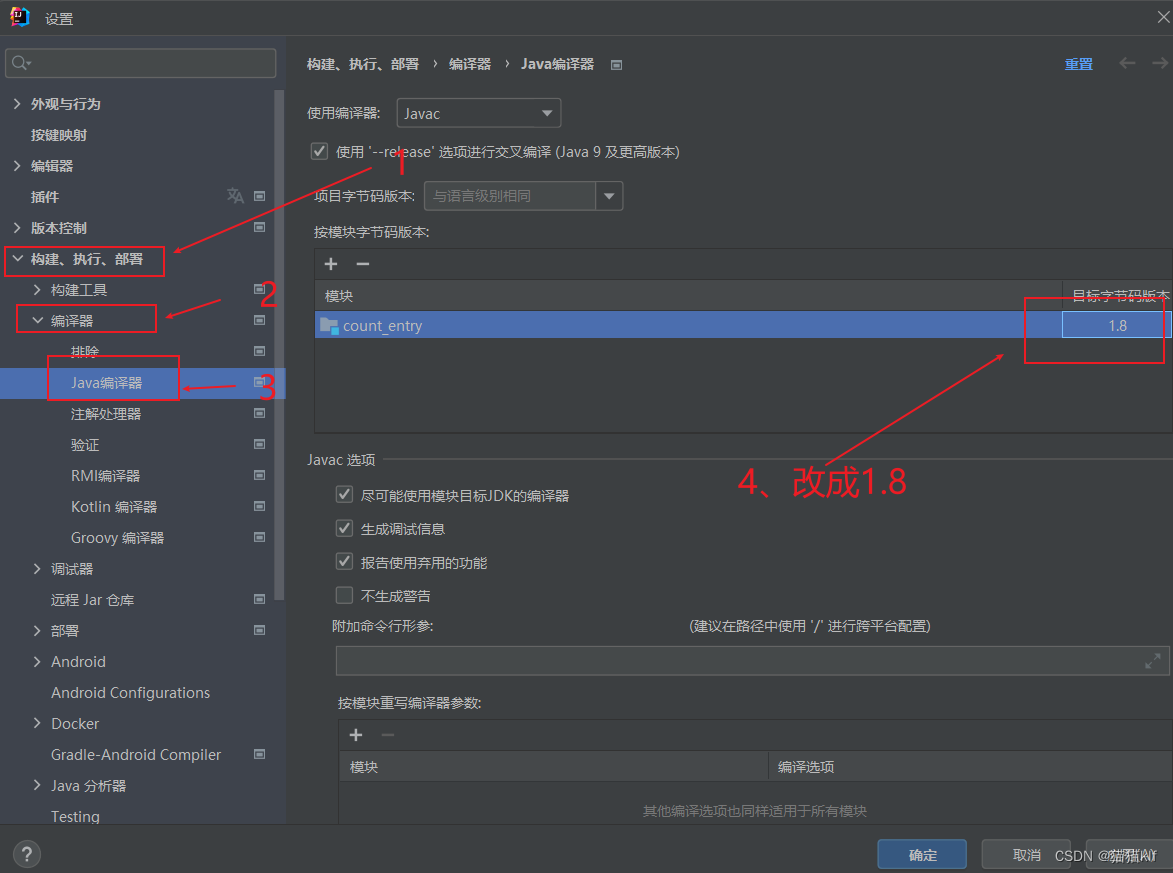
解决:IDEA编译Java程序时报编译失败
1、问题展示: 2、解决方法:...

vue+vite根据版本号清空用户浏览器缓存
项目生产环境发布新版本之后,用户可能会因为一些本地缓存的数据不一样而导致页面报错。这时候可以根据版本号去清空用户缓存。 1、在package.json文件中有一个管理版本号属性:version,在每次打包部署之前修改当前版本号。 2、在main.js文件中…...

AXI CANFD MicroBlaze 测试笔记
文章目录 前言测试用的硬件连接Vivado 配置Vitis MicroBlaze CANFD 代码测试代码测试截图Github Link 前言 官网: CAN with Flexible Data Rate (CAN FD) (xilinx.com) 特征: 支持8Mb/s的CANFD多达 3 个数据位发送器延迟补偿(TDC, transmitter delay compensation)32-deep T…...
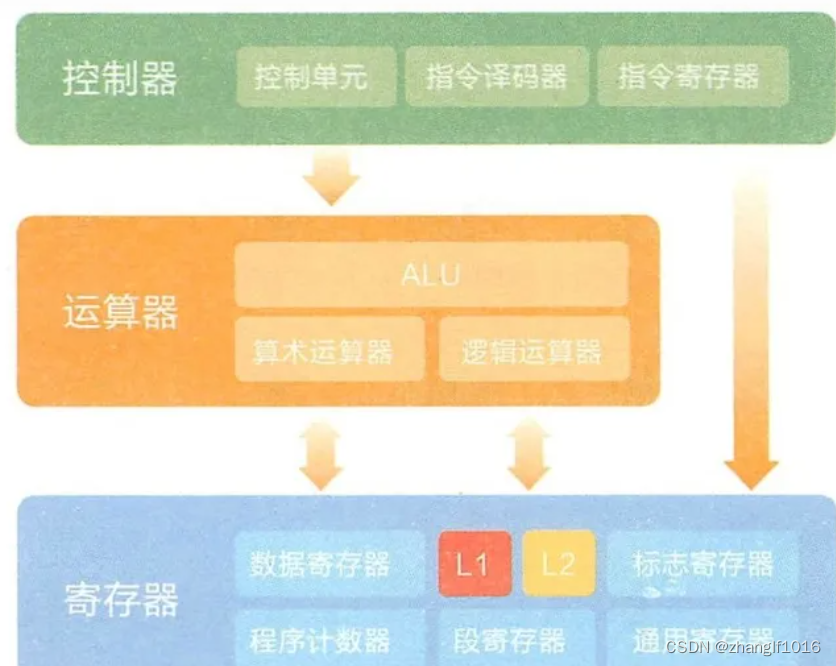
操作系统——cpu、内存、缓存介绍
一、内存是什么 内存就是系统资源的代名词,它是其他硬件设备与 CPU 沟通的桥梁, 计算机中的所有程序都在内存中运行。其作用是暂时存放CPU的运算数据,以及与硬盘交换的数据。也是相当于CPU与硬盘沟通的桥梁。只要计算机在运行,CP…...
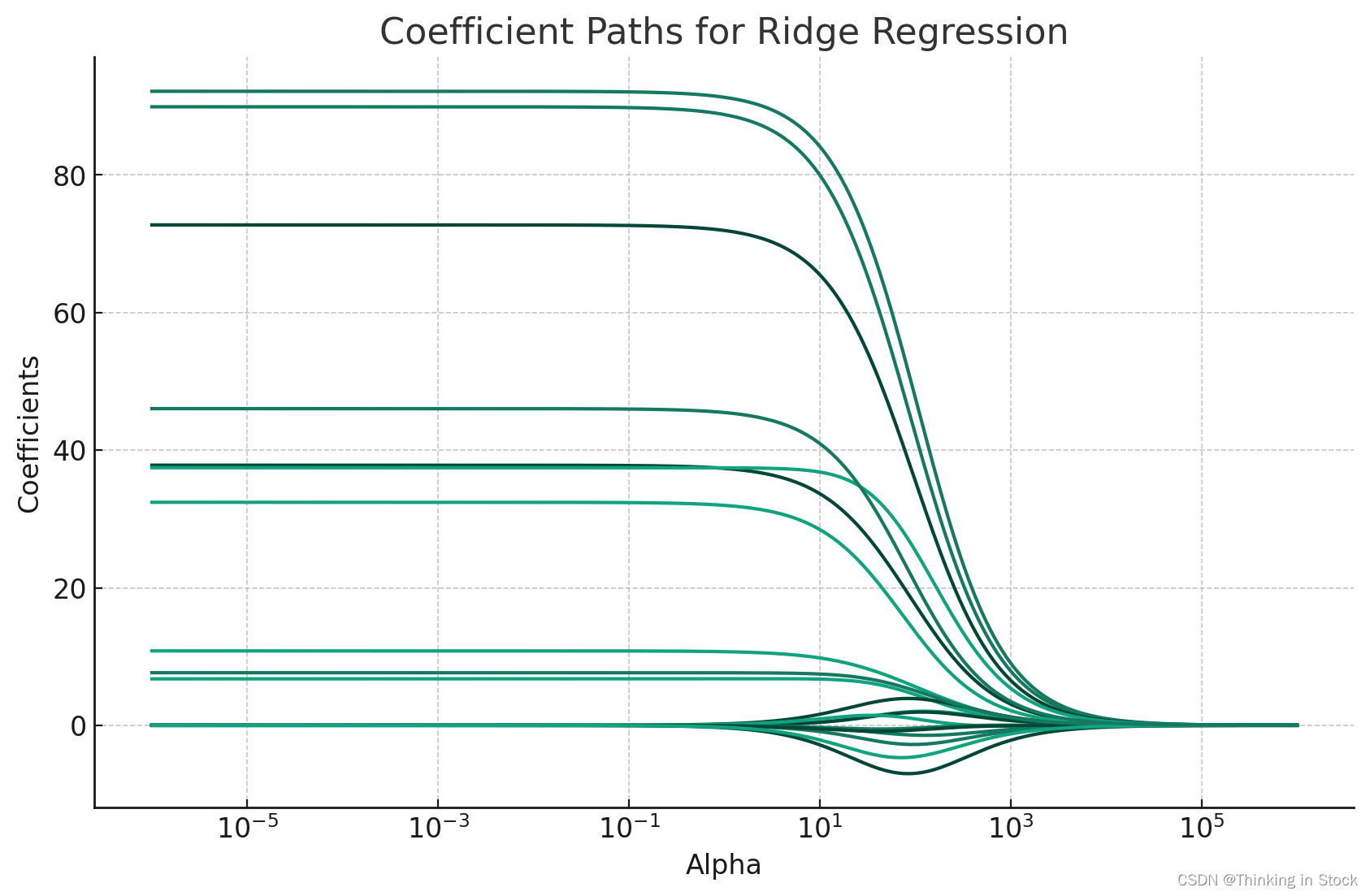
【理解机器学习算法】之岭回归Ridge - L2 Rgularization
Ridge 回归(Ridge Regression)也称作岭回归或脊回归,是一种专用于共线性数据分析的有偏估计回归方法。在多元线性回归中,如果数据集中的特征(自变量)高度相关,也就是说存在共线性(Multicollinea…...
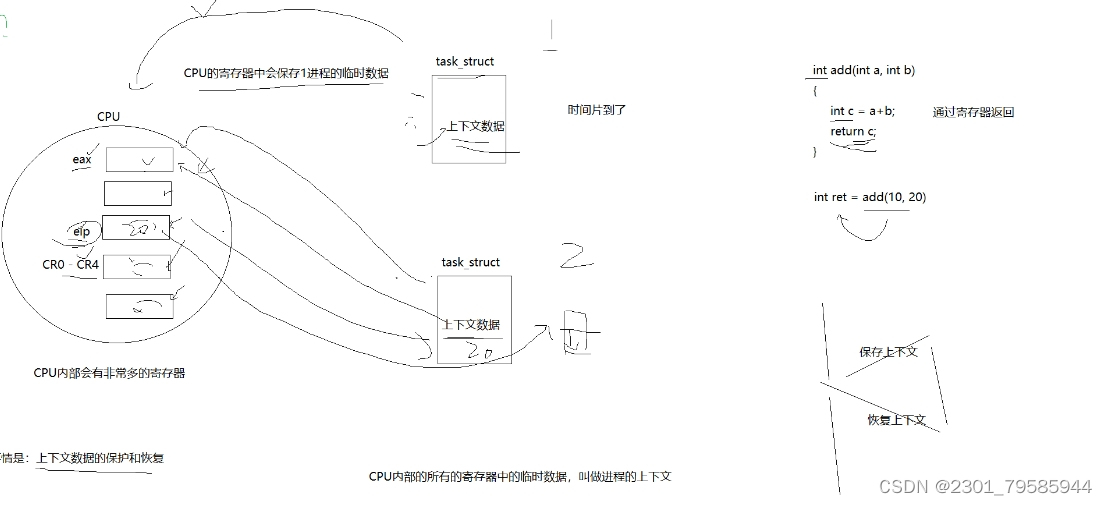
【Linux进程状态】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、直接谈论Linux的进程状态 看看Linux内核源代码怎么说 1.1、R状态 -----> 进程运行的状态 1.2、S状态 -----> 休眠状态(进程在等待“资源”就绪) 1.3、T状…...

【RS422】基于未来科技FT4232HL芯片的多波特率串口通信收发实现
功能简介 串行通信接口常常用于在计算机和低速外部设备之间传输数据。串口通信存在多种标准,以RS422为例,它将数据分成多个位,采用异步通信方式进行传输。 本文基于Xilinx VCU128 FPGA开发板,对RS422串口通信进行学习。 根…...
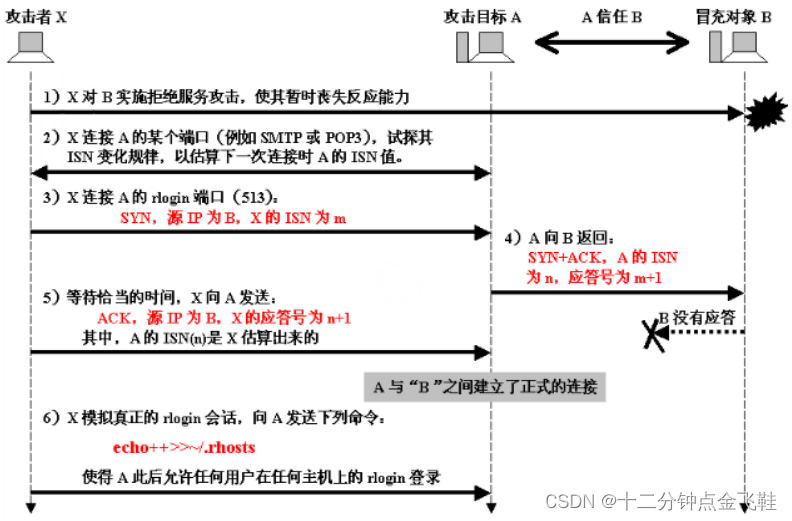
Internet协议的安全性
Internet协议的安全性 文章目录 Internet协议的安全性1. 网络层1. IP*62. ARP*33. ICMP * 3 2. 传输层协议1. TCP1. * SYN-Flood攻击攻击检测* 防御 2. TCP序号攻击攻击 3. 拥塞机制攻击 2. UDP 3. 应用层协议1. DNS攻击*3防范*3: 2. FTP3. TELNET: 改用ssh4. 电子邮件1. 攻击2…...

LeetCode每日一题——移除元素
移除元素OJ链接:27. 移除元素 - 力扣(LeetCode) 题目: 思路: 题目给定要求只能使用O(1)的额外空间并且原地修改输入数组,然后返回移除后的数组行长度。那 么我们就可以确我没有办法建立临时的数组存放我…...

vue3之自定义指令
除了 Vue 内置的一系列指令 (比如 v-model 或 v-show) 之外,Vue 还允许你注册自定义的指令。自定义指令主要是为了重用涉及普通元素的底层 DOM 访问的逻辑。 写法 1. 没有使用 <script setup>的情况下 export default {setup() {/*...*/},directives: {// 在…...

MySQL语法分类 DQL(5)分组查询
为了更好的学习这里给出基本表数据用于查询操作 create table student (id int, name varchar(20), age int, sex varchar(5),address varchar(100),math int,english int );insert into student (id,name,age,sex,address,math,english) values (1,马云,55,男,杭州,66,78),…...

C++程序设计-练手题集合【期末复习|考研复习】
前言 总结整理不易,希望大家点赞收藏。 给大家整理了一下C程序设计中的练手题,以供大家期末复习和考研复习的时候使用。 C程序设计系列文章传送门: 第一章 面向对象基础 第四/五章 函数和类和对象 第六/七/八章 运算符重载/包含与继承/虚函数…...
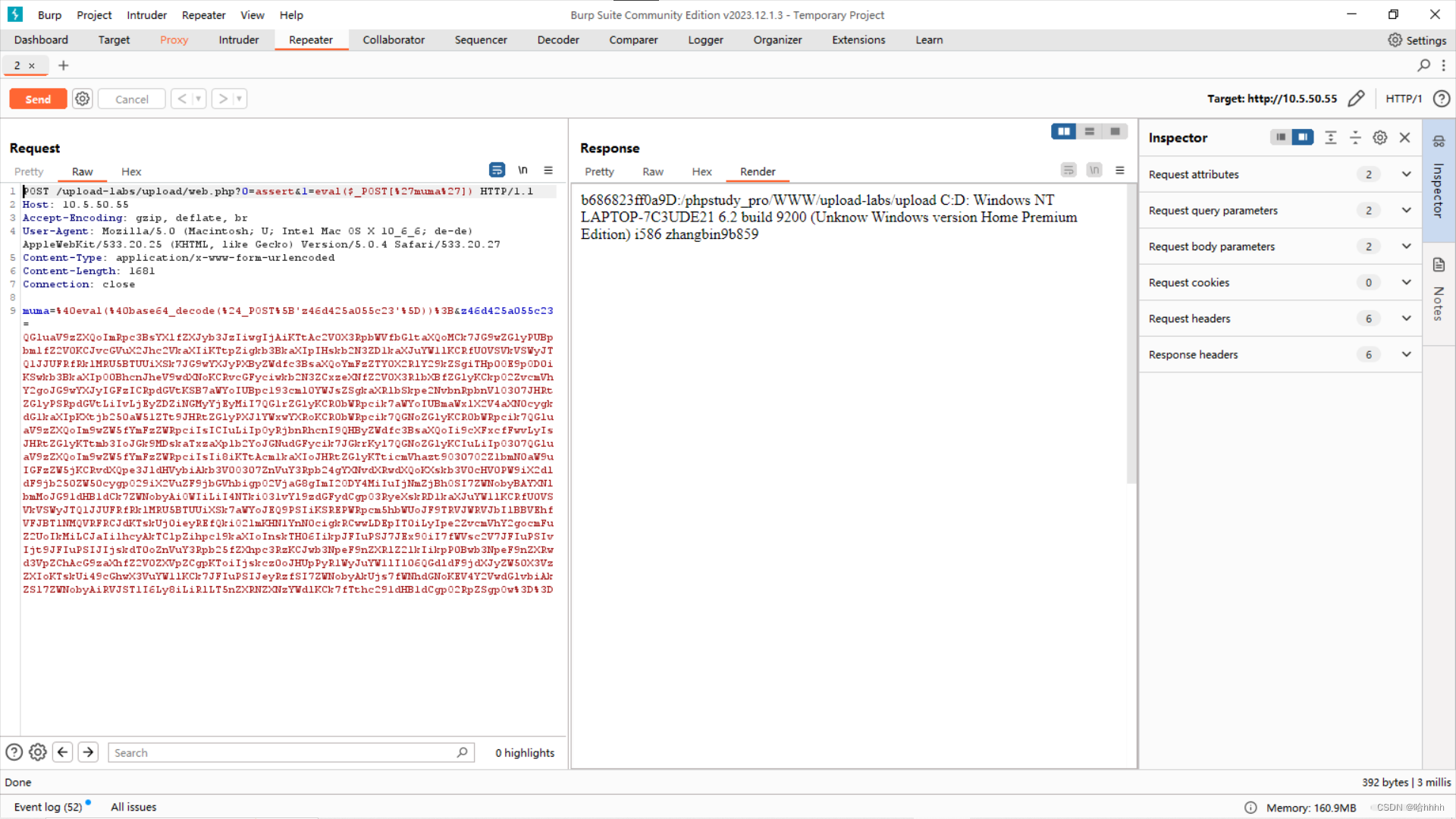
文件上传漏洞------一句话木马原理解析
目录 一、实验环境 二、实验过程 构造一句话木马 一句话木马的使用: 木马原理解析: 一、实验环境 小皮面板搭建:upload-labs靶场 二、实验过程 构造一句话木马 这是一个最简单的一句话木马,我们用GET传参接受了两个参数,其最终目的是构造出:ass…...

Openfeign使用教程(带你快速体验Openfeign的便捷)
文章摘要 本文中将教会您如何快速使用Openfeign,包括Opengfeign的基础配置、接口调用、接口重试、拦截器实现、记录接口日志信息到数据库 文章目录 文章摘要一、Openfeign初步定义二、Openfeign快速入门1.引入maven坐标2.启动类增加EnableFeignClients注解3.定义fei…...
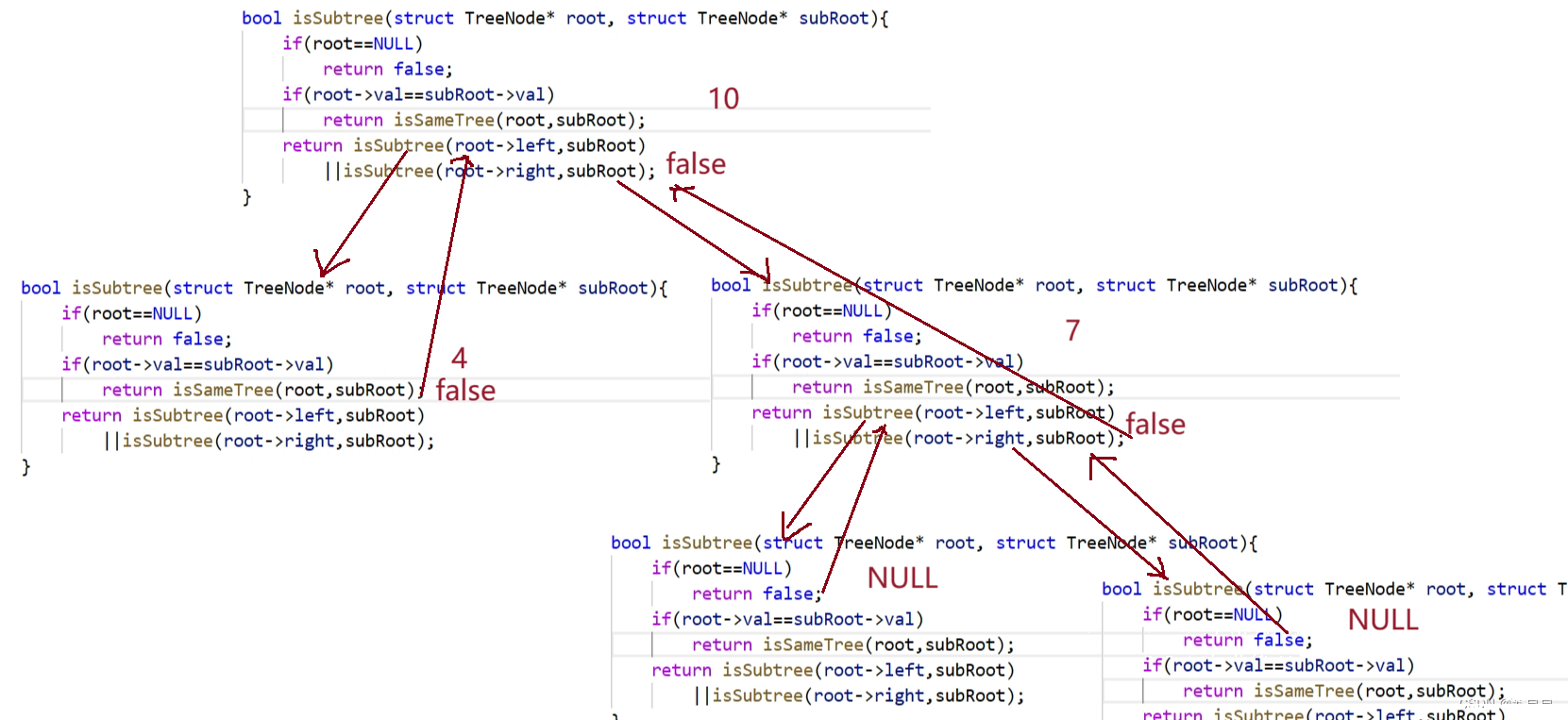
【leetcode】相同的树➕对称二叉树➕另一棵树的子树
大家好,我是苏貝,本篇博客带大家刷题,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 一. 相同的树二. 对称二叉树三. 另一棵树的子树 一. 相同的树 点击查看题目 思路: bool isSameTree(…...

uni-app 安卓手机判断是否开启相机相册权限
// 安卓相机权限 androidCameraPermiss(index){ plus.android.requestPermissions([android.permission.CAMERA],(e) > { if (e.deniedAlways.length > 0) { this.androidAuthCamera false …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
