BFS 求解 最小高度树 【妙用】
310. 最小高度树
链接 :题目链接
- 思路
- 常规解法是树形dp,两个dfs解决,这里不再赘述
- 新颖解法bfs,而且实现更加简单,大体思路就是每次都从叶子节点一步步往中心爬,最后一批留在队列中的节点就为本题意的答案,具体实现思路就是每次更新叶子节点,也就是把之前的叶子节点扔掉,然后和它相连的节点度数减一产生新的叶子节点。
代码
class Solution {
public:vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {if(n == 1) return {0};vector<int> out(n+10);// 统计每个点的出度vector<vector<int>> e(n+10);for(auto i : edges){int a = i[0];int b = i[1];out[a] ++, out[b] ++;e[b].push_back(a);// 建立邻接表e[a].push_back(b);}vector<int> res;queue<int> q;for(int i = 0; i < n; i ++){if(out[i] == 1)// 先让出度为1的点入队{q.push(i);}}while(q.size()){res.clear();// res 存储当下遍历完的节点int num = q.size();for(int i = 0; i < num; i ++){int x = q.front();q.pop();res.push_back(x);for(auto it : e[x]){out[it] --;// 与该点连接的点 出度减一if(out[it] == 1)// 添加新的"叶子节点"{q.push(it);}}}}return res;}
};
思路来自 大佬小鑫
相关文章:

BFS 求解 最小高度树 【妙用】
310. 最小高度树 链接 :题目链接 思路 常规解法是树形dp,两个dfs解决,这里不再赘述新颖解法bfs,而且实现更加简单,大体思路就是每次都从叶子节点一步步往中心爬,最后一批留在队列中的节点就为本题意的答案…...
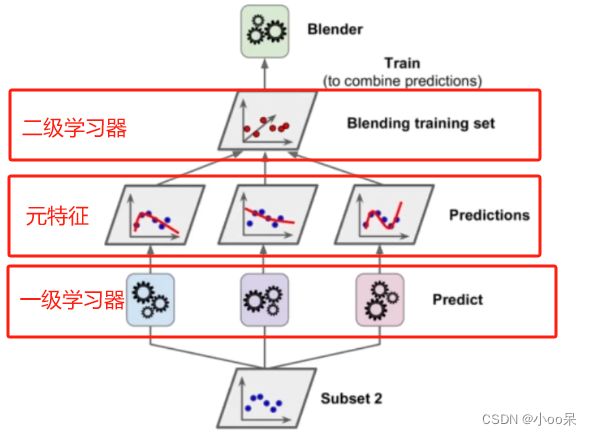
【机器学习300问】36、什么是集成学习?
一、什么是集成学习? (1)它的出现是为了解决什么问题? 提高准确性:单个模型可能对某些数据敏感或者有概念偏见,而集成多个模型可以提高预测的准确性。让模型变稳定:一些模型,如决策…...

Stargo 管理部署 Starrocks 集群
配置主机间 ssh 互信 ssh-copy-id hadoop02 ssh-copy-id hadoop03配置系统参数 ############################ Swap检查 ############################ echo 0 | sudo tee /proc/sys/vm/swappiness########################### 内核参数检查 ########################## echo…...
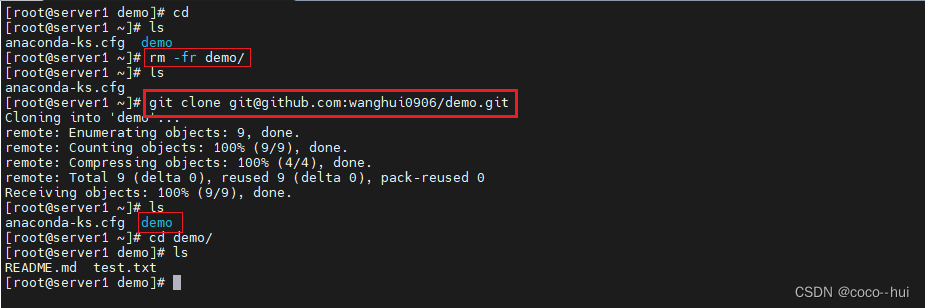
CI/CD实战-git工具使用 1
版本控制系统 本地版本控制系统 集中化的版本控制系统 分布式版本控制系统 git官网文档:https://git-scm.com/book/zh/v2 Git 有三种状态:已提交(committed)、已修改(modified) 和 已暂存(sta…...
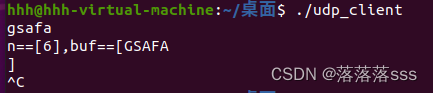
Linux中udp服务端,客户端的开发
UDP通信相关函数: ssize_t recvfrom(int sockfd, void *buf, size_t len, int flags, struct sockaddr *src_addr, socklen_t *addrlen); 函数说明:接收信息 参数说明:sockfd:套接字buf:要接收的缓冲区len:缓冲区…...
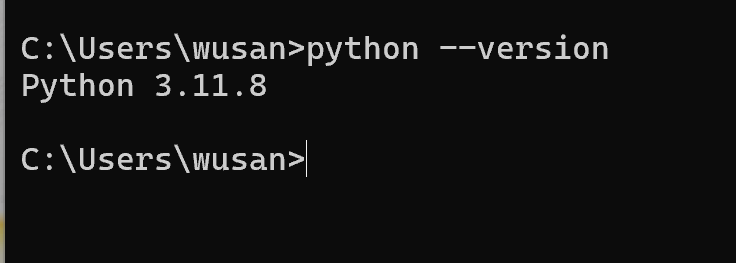
1.python安装
1.检查是否已经安装python 打开cmd 输入 python --version查看是否有返回版本,没有返回则环境变量未设置好,或者未安装 2.下载安转python https://www.python.org/downloads/windows/ 勾选配置环境变量路径 安装成功...

【Flink SQL】Flink SQL 基础概念(三):SQL 动态表 连续查询
《Flink SQL 基础概念》系列,共包含以下 5 篇文章: Flink SQL 基础概念(一):SQL & Table 运行环境、基本概念及常用 APIFlink SQL 基础概念(二):数据类型Flink SQL 基础概念&am…...

科研绘图一:箱线图(添加贝赛尔曲线)
R语言绘图系列—箱线图贝赛尔曲线 (一): 科研绘图一:箱线图(添加贝赛尔曲线) 文章目录 R语言绘图系列---箱线图贝赛尔曲线(一): 科研绘图一:箱线图(添加贝赛尔曲线&…...

最佳实践:Swagger 自动生成 Api 文档
自动生成 API 文档的好处不言而喻,它可以提供给你的团队或者外部协作者,方便 API 使用者准确地调用到你的 API。为了降低手动编写文档带来的错误,很多 API 开发者会偏向于寻找一些好的方法来自动生成 API 文档。本文将会介绍一些常用的文档生…...

搬砖。。。
0搬砖 - 蓝桥云课 (lanqiao.cn) 问题描述 这天,小明在搬砖 他一共有n块砖他发现第砖的重量为w价值为i。他突然想从这些砖中选一些出来从下到上堆成一座塔,并且对于塔中的每一块砖来说,它上面所有砖的重量和不能超过它自身的价值。 他想知道这样堆成的塔的…...
【论文笔记合集】Transformers in Time Series A Survey综述总结
本文作者: slience_me 文章目录 Transformers in Time Series A Survey综述总结1 Introduction2 Transformer的组成Preliminaries of the Transformer2.1 Vanilla Transformer2.2 输入编码和位置编码 Input Encoding and Positional Encoding绝对位置编码 Absolute …...

HarmonyOS(二十)——管理应用拥有的状态之LocalStorage(页面级UI状态存储)
LocalStorage是页面级的UI状态存储,通过Entry装饰器接收的参数可以在页面内共享同一个LocalStorage实例。LocalStorage也可以在UIAbility实例内,在页面间共享状态。 本文仅介绍LocalStorage使用场景和相关的装饰器:LocalStorageProp和LocalS…...
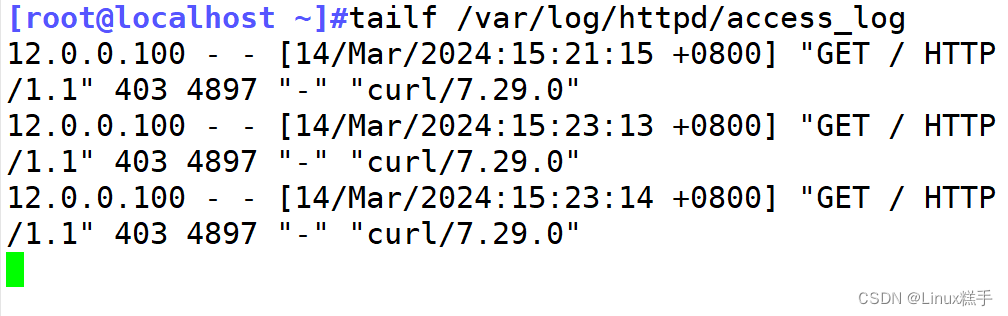
Linux系统安全②SNAT与DNAT
目录 一.SNAT 1.定义 2.实验环境准备 (1)三台服务器:PC1客户端、PC2网关、PC3服务端。 (2)硬件要求:PC1和PC3均只需一块网卡、PC2需要2块网卡 (3)网络模式要求:PC1…...
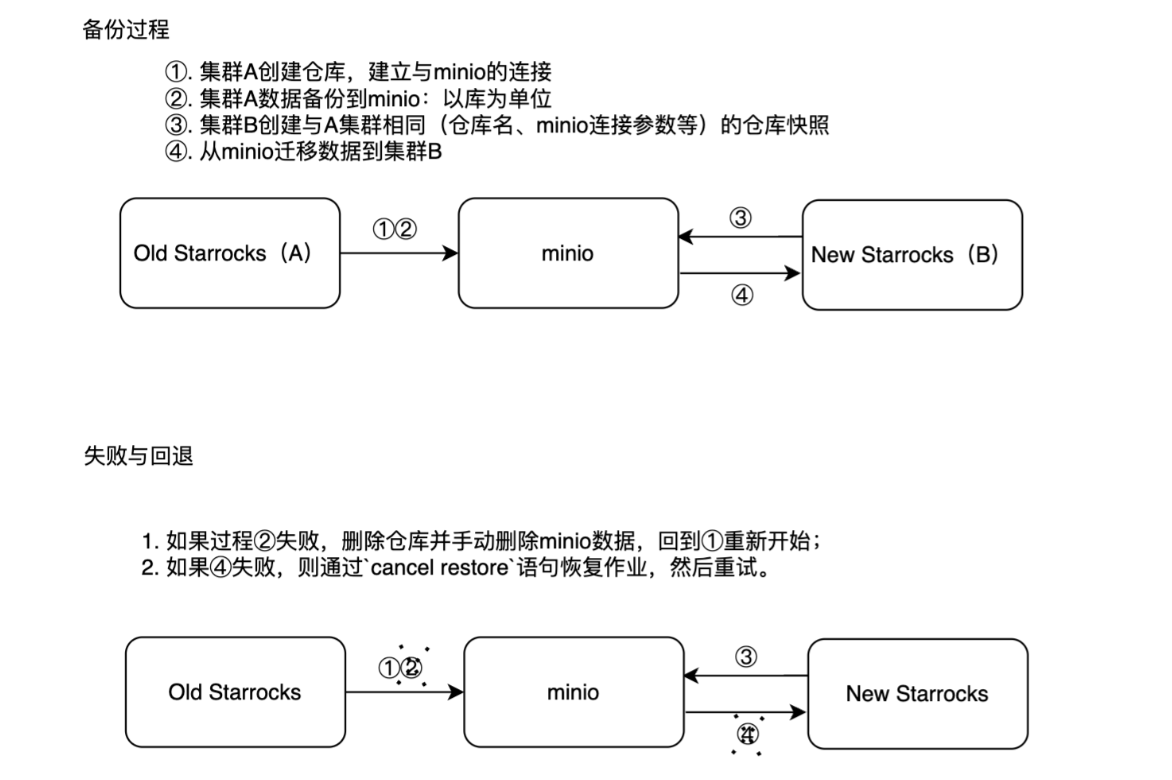
【运维】StarRocks数据迁移到新集群(针对于集群互通、不互通的情况)
文章目录 一. 迁移整体思路1. 对于新旧集群互通的情况2. 对于新旧集群不互通的情况二、迁移过程(两个集群互通的情况)1. 备份过程1.1. 通过mysqlclient与starrocks进行关联1.2. 创建仓库与minio建立联系1.3. 备份数据到minio2. 迁移过程2.1. 通过mysqlclient与starrocks进行关…...
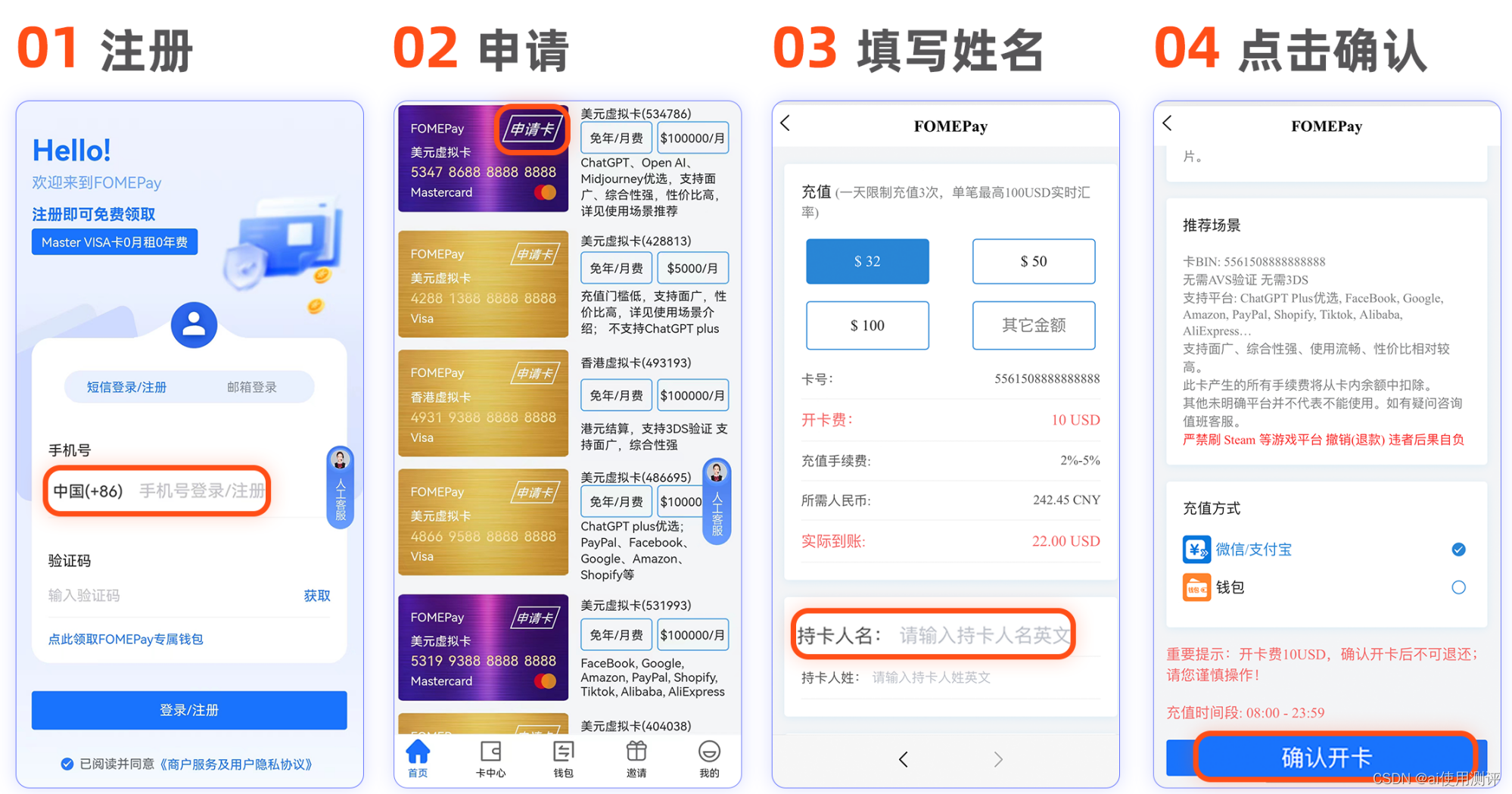
facebook个人广告账户充值方式有哪些?看这一篇就够了
可以使用虚拟信用卡进行充值,也可以使用虚拟卡绑定paypal进行充值 点击获取虚拟卡 开卡步骤如下图 Facebook如何添加支付方式 1.前往支付设置。 2.在支付方式版块,点击添加支付方式。 3.选择要添加的支付方式,填写相关信息,然…...

蓝桥杯算法练习系统—作物杂交【第十一届】【省赛】【C组】
问题描述 作物杂交是作物栽培中重要的一步。已知有 N 种作物(编号 1 至 N ),第 i 种作物从播种到成熟的时间为 Ti。 作物之间两两可以进行杂交,杂交时间取两种中时间较长的一方。如作物 A 种植时间为 5 天,作物 B 种植时间为 7 天࿰…...
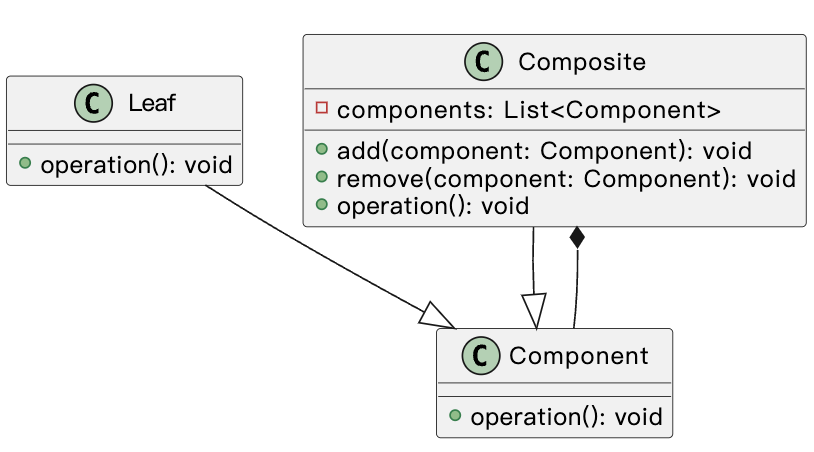
java组合模式揭秘:如何构建可扩展的树形结构
组合模式(Composite Pattern)是一种结构型设计模式,它允许将对象组合成树形结构以表示整体/部分层次结构。组合模式使得客户端可以统一对待单个对象和组合对象,从而使得客户端可以处理更复杂的结构。 组合模式的主要组成部分包括&…...
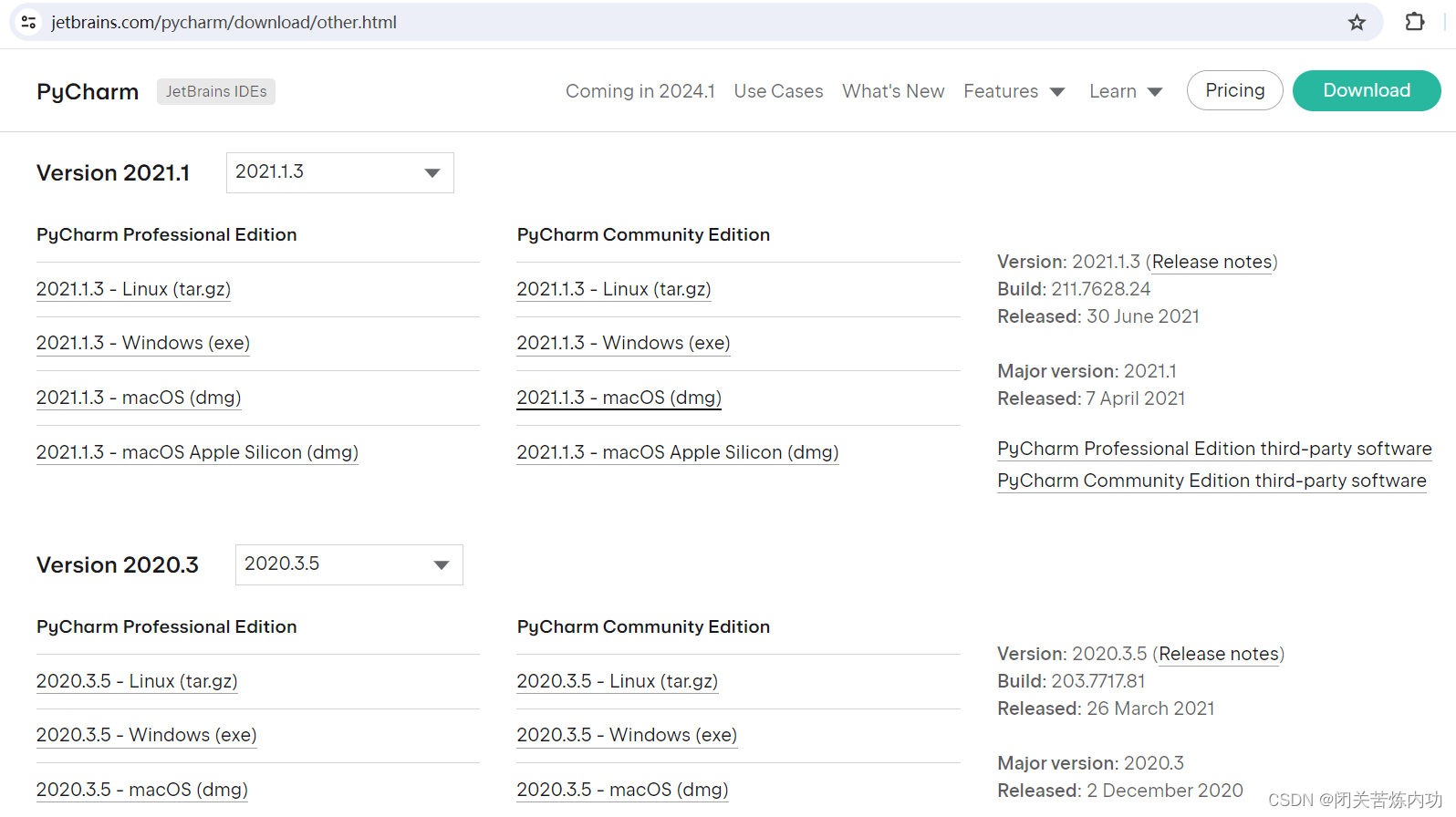
pycharm 历史版本下载地址
pycharm 历史版本下载地址 老版本能用就行,不需要搞最新的,当然了,有些小伙伴就是喜欢新的(最先吃螃蟹) 博主就不搞最新了,哈哈 上菜: https://www.jetbrains.com/pycharm/download/other.html…...
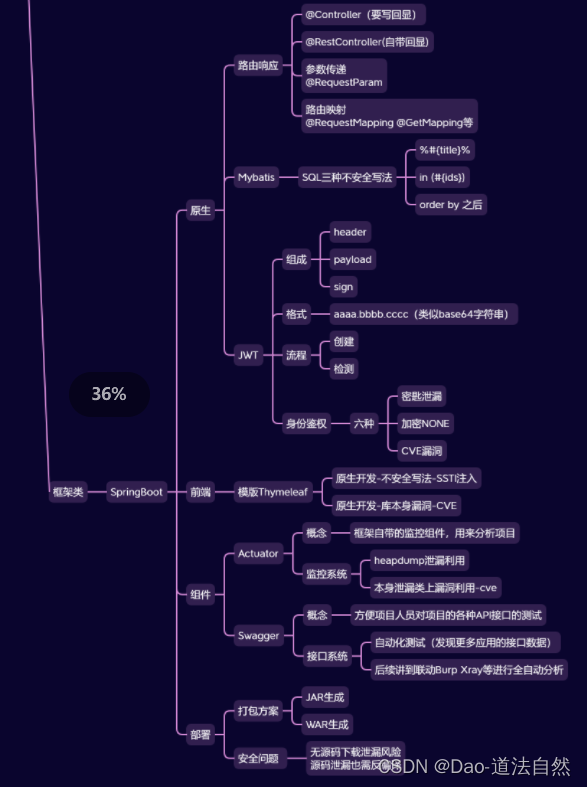
Day39:安全开发-JavaEE应用SpringBoot框架Actuator监控泄漏Swagger自动化
目录 SpringBoot-监控系统-Actuator SpringBoot-接口系统-Swagger 思维导图 Java知识点: 功能:数据库操作,文件操作,序列化数据,身份验证,框架开发,第三方组件使用等. 框架库:MyB…...
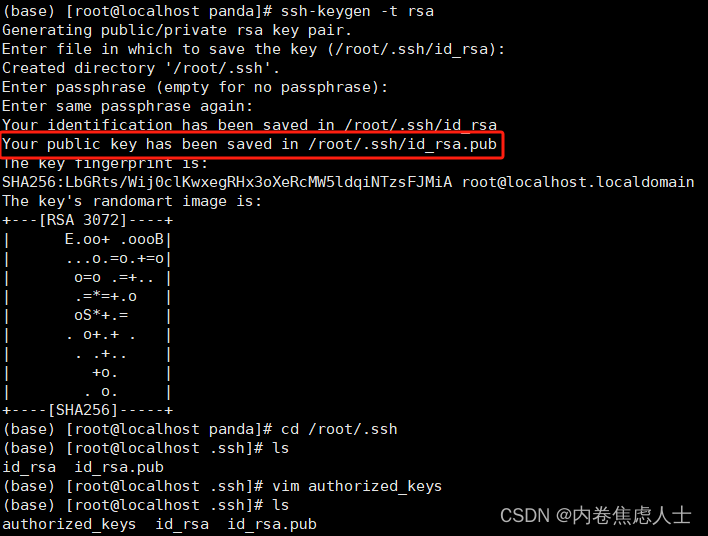
VsCode免密登录
创建本地密匙 按下WinR输入cmd,输入 ssh-keygen -t rsa然后连续回车直到结束 找到Your public key has been saved in C:\Users\Administrator/.ssh/id_rsa.pub,每个人都不一样找到密匙所在地 打开id_rsa.pub这个文件,可以用记事本打开&am…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
